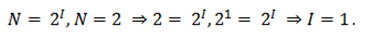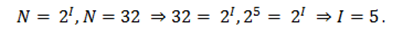Уравнение хартли привести примеры записать формулу

Уравнение хартли привести примеры записать формулу

1.2. Формула Хартли измерения количества информации. Закон аддитивности информации

Как уже упоминалось выше, в качестве основной единицы измерения информации мы будем использовать бит. Соответственно, с точки зрения алфавитного подхода мы будем кодировать информацию при помощи нулей и единиц (двоичных знаков).

Для того чтобы измерить количество информации в сообщении, надо закодировать сообщение в виде последовательности нулей и единиц наиболее рациональным способом, позволяющим получить самую короткую последовательность. Длина полученной последовательности нулей и единиц и является мерой количества информации в битах.

Поставим себе одну из наиболее часто встречающихся задач в теории информации. Пусть у нас есть `N` возможных равновероятных вариантов исходов некоторого события. Какое количество информации нам нужно получить, чтобы оставить только один вариант?

Например, пусть мы знаем, что некоторая интересная для нас книга находится на одной из полок нашего книжного шкафа, в котором `8` полок. Какое количество информации нам нужно получить, чтобы однозначно узнать полку, на которой находится книга?

Решим эту задачу с точки зрения содержательного и алфавитного подходов. Поскольку изначально в шкафу было `8` полок, а в итоге мы выберем одну, следовательно, неопределённость знания о местоположении книги уменьшится в `8` раз. Мы говорили, что один бит – это количество информации, уменьшающее неопределённость знания в `2` раза. Следовательно, мы должны получить `3` бита информации.

Теперь попробуем использовать алфавитный подход. Закодируем номера всех полок при помощи `0` и `1`. Получим следующие номера: `000, 001, 010, 011, 100, 101, 110, 111`. Для того чтобы узнать, на какой полке находится книга, мы должны узнать номер этой полки. Каждый номер состоит из `3` двоичных знаков. А по определению, `1` бит (в алфавитном подходе) – это количество информации в сообщении, состоящем из `1` двоичного знака. То есть мы тоже получим `3` бита информации.

Прежде чем продолжить рассмотрение поставленной общей задачи введём важное математическое определение.

Назовём логарифмом числа `N` по основанию `a` такое число `X`, что Обозначение:

На параметры логарифма налагаются некоторые ограничения. Число `N` обязательно должно быть строго больше `0`. Число `a` (основание логарифма) должно быть также строго больше нуля и при этом не равняться единице (ибо при возведении единицы в любую степень получается единица).

Теперь вернёмся к нашей задаче. Итак, какое же количество информации нам нужно получить, чтобы выбрать один исход из `N` равновероятных? Ответ на этот вопрос даёт формула Хартли: `H=log_aN`, где `N` – это количество исходов, а `H` – количество информации, которое нужно получить для однозначного выбора `1` исхода. Основание логарифма обозначает единицу измерения количества информации. То есть если мы будем измерять количество информации в битах, то логарифм нужно брать по основанию `2`, а если основной единицей измерения станет трит, то, соответственно, логарифм берётся по основанию `3`.

Рассмотрим несколько примеров применения формулы Хартли.

В библиотеке `16` стеллажей, в каждом стеллаже `8` полок. Какое количество информации несёт сообщение о том, что нужная книга находится на четвёртой полке?

Решим эту задачу с точки зрения содержательного подхода. В переданном нам сообщении указан только номер полки, но не указан номер стеллажа. Таким образом, устранилась неопределённость, связанная с полкой, а стеллаж, на котором находится книга, мы всё ещё не знаем. Так как известно, что в каждом стеллаже по `8` полок, следовательно, неопределённость уменьшилась в `8` раз. Следовательно, количество информации можно вычислить по формуле Хартли `H=log_2 8=3` бита информации.

Имеется `27` монет, одна из которых фальшивая и легче всех остальных. Сколько потребуется взвешиваний на двухчашечных весах, чтобы однозначно найти фальшивую монету?

В этой задаче неудобно использовать бит в качестве основной единицы измерения информации. Двухчашечные весы могут принимать три положения: левая чаша перевесила, значит, фальшивая монета находится в правой; правая чаша перевесила, значит, монета находится в левой; или же весы оказались в равновесии, что означает отсутствие фальшивой монеты на весах. Таким образом, одно взвешивание может уменьшить неопределённость в три раза, следовательно, будем использовать в качестве основной единицы измерения количес-тва информации трит.

По формуле Хартли `H = log _3 27 = 3` трита. Таким образом, мы видим, что для того чтобы найти фальшивую монету среди остальных, нам потребуется три взвешивания.

Логарифмы обладают очень важным свойством: `log_a(X*Y)=log_aX+log_aY`.

Если переформулировать это свойство в терминах количества информации, то мы получим закон аддитивности информации: Коли-чество информации`H(x_1, x_2)`, необходимое для установления пары `(x_1, x_2)`, равно сумме количеств информации `H(x_1)` и `H(x_2)`, необходимых для независимого установления элементов `x_1` и `x_2`:

Проиллюстрируем этот закон на примере. Пусть у нас есть игральная кость в форме октаэдра (с `8` гранями) и монета. И мы одновременно подбрасываем их вверх. Нужно узнать, какое количество информации несёт сообщение о верхней стороне монеты после падения (орёл или решка) и числе, выпавшему на игральной кости.

Игральная кость может упасть `8` различными способами, следовательно, по формуле Хартли можно вычислить, что, определив число, выпавшее на игральной кости, мы получаем `3` бита информации. Соответственно, монета может упасть только `2` способами и несёт в себе `1` бит информации. По закону аддитивности информации мы можем сложить полученные результаты и узнать, что интересующее нас сообщение несёт `4` бита информации.

Рассмотрим другой способ решения этой задачи. Если мы сразу рассмотрим все возможные исходы падения `2` предметов, то их будет `16` (кость выпадает `8` способами, а монета — орлом вверх, и кость выпадает `8` способами, а монета — решкой вверх). По формуле Хартли находим, что интересующее нас сообщение несёт `4` бита информации.

Если в результате вычислений по формуле Хартли получилось нецелое число, а в задаче требуется указать целое число бит, то результат следует округлить в большую сторону.

Опорный конспект на тему «Формулы Хартли-Шеннона»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

«Актуальность создания школьных служб примирения/медиации в образовательных организациях»

Свидетельство и скидка на обучение каждому участнику

Формулы Хартли, Шеннона.

В 1928 г. американский инженер Р. Хартли предложил научный подход к оценке сообщений. Предложенная им формула имела следующий вид:

где К — количество равновероятных событий; I — количество бит в сообщении, такое, что любое из К событий произошло. Тогда K=2 I .

Иногда формулу Хартли записывают так:

I = log ₂ K = log ₂ (1 / р ) = — log ₂ р

т. к. каждое из К событий имеет равновероятный исход р = 1 / К, то К = 1 / р.

Шарик находится в одной из трех урн: А, В или С. Определить сколько бит информации содержит сообщение о том, что он находится в урне В.

Такое сообщение содержит I = log ₂ 3 = 1,585 бита информации.

Но не все ситуации имеют одинаковые вероятности реализации. Существует много таких ситуаций, у которых вероятности реализации различаются. Например, если бросают несимметричную монету или «правило бутерброда».

«Однажды в детстве я уронил бутерброд. Глядя, как я виновато вытираю масляное пятно, оставшееся на полу, старший брат успокоил меня:

— не горюй, это сработал закон бутерброда.

— Что еще за закон такой? — спросил я.

— Закон, который гласит: «Бутерброд всегда падает маслом вниз». Впрочем, это шутка, — продолжал брат. — Никакого закона нет. Просто бутерброд действительно ведет себя довольно странно: большей частью масло оказывается внизу.

— Давай-ка еще пару раз уроним бутерброд, проверим, — предложил я. — Все равно ведь его придется выкидывать.

Проверили. Из десяти раз восемь бутерброд упал маслом вниз.

И тут я задумался: а можно ли заранее узнать, как сейчас упадет бутерброд маслом вниз или вверх?

Наши опыты прервала мать…»

( Отрывок из книги «Секрет великих полководцев», В.Абчук).

В 1948 г. американский инженер и математик К. Шеннон предложил формулу для вычисления количества информации для событий с различными вероятностями.

Если I — количество информации,

К — количество возможных событий,

р _i — вероятности отдельных событий,

то количество информации для событий с различными вероятностями можно определить по формуле:

где i принимает значения от 1 до К.

Формулу Хартли теперь можно рассматривать как частный случай формулы Шеннона:

I = — Sum 1 / К log ₂ (1 / К ) = I = log ₂ К .

При равновероятных событиях получаемое количество информации максимально.

Физиологи и психологи научились определять количество информации, которое человек может воспринимать при помощи органов чувств, удерживать в памяти и подвергать обработке. Информацию можно представлять в различных формах: звуковой, знаковой и др. рассмотренный выше способ определения количества информации, получаемое в сообщениях, которые уменьшают неопределенность наших знаний, рассматривает информацию с позиции ее содержания, новизны и понятности для человека. С этой точки зрения в опыте по бросанию кубика одинаковое количество информации содержится в сообщениях «два», «вверх выпала грань, на которой две точки» и в зрительном образе упавшего кубика.

При передаче и хранении информации с помощью различных технических устройств информацию следует рассматривать как последовательность знаков (цифр, букв, кодов цветов точек изображения), не рассматривая ее содержание.

Считая, что алфавит (набор символов знаковой системы) — это событие, то появление одного из символов в сообщении можно рассматривать как одно из состояний события. Если появление символов равновероятно, то можно рассчитать, сколько бит информации несет каждый символ. Информационная емкость знаков определяется их количеством в алфавите. Чем из большего количества символов состоит алфавит, тем большее количество информации несет один знак. Полное число символов алфавита принято называть мощностью алфавита.

Молекулы ДНК (дезоксирибонуклеиновой кислоты) состоят из четырех различных составляющих (нуклеотидов), которые образуют генетический алфавит. Информационная емкость знака этого алфавита составляет:

4 = 2 I , т.е. I = 2 бит.

Каждая буква русского алфавита (если считать, что е=ё) несет информацию 5 бит (32 = 2 I ).

При таком подходе в результате сообщения о результате бросания кубика, получим различное количество информации, Чтобы его подсчитать, нужно умножить количество символов на количество информации, которое несет один символ.

Количество информации, которое содержит сообщение, закодированное с помощью знаковой системы, равно количеству информации, которое несет один знак, умноженному на число знаков в сообщении.

Пример 1. Использование формулы Хартли для вычисления количества информации. Сколько бит информации несет сообщение о том, что

поезд прибывает на один из 8 путей?

где N – число равновероятностных исходов события, о котором речь идет в сообщении,

I – количество информации в сообщении.

I = log ₂ 8 = 3(бит) Ответ: 3 бита.

Модифицированная формула Хартли для неравновероятностных событий. Так как наступление каждого из N возможных событий имеет одинаковую вероятность

p = 1 / N , то N = 1 / p и формула имеет вид

Количественная зависимость между вероятностью события (p) и количеством информации в сообщении о нем (I) выражается формулой:

Вероятность события вычисляется по формуле p=K/N , K – величина, показывающая, сколько раз произошло интересующее нас событие; N – общее число возможных исходов, событий. Если вероятность уменьшается, то количество информации увеличивается.

Пример 2. В классе 30 человек. За контрольную работу по математике получено 6 пятерок, 15 четверок, 8 троек и 1 двойка. Сколько бит информации несет сообщение о том, что Иванов получил четверку?

Количественная зависимость между вероятностью события (p) и количество информации сообщения о нем (I)

вероятность события 15/30

количество информации в сообщении =log ₂ (30/15)=log ₂ 2=1.

Использование формулы Шеннона. Общий случай вычисления количества информации в сообщении об одном из N, но уже неравновероятных событий. Этот подход был предложен К.Шенноном в 1948 году.

Основные информационные единицы:

Iср — количество бит информации, приходящееся в среднем на одну букву;

M — количество символов в сообщении

I – информационный объем сообщения

p _i -вероятность появления i символа в сообщении; i — номер символа;

I _ср = —

Значение I _ср достигает максимума при равновероятных событиях, то есть при равенстве всех p _i p _i = 1 / N.

В этом случае формула Шеннона превращается в формулу Хартли.

Пример 3. Сколько бит информации несет случайно сгенерированное сообщение «фара», если в среднем на каждую тысячу букв в русских текстах буква «а» встречается 200 раз, буква «ф» — 2 раза, буква «р» — 40 раз.

Будем считать, что вероятность появления символа в сообщении совпадает с частотой его появления в текстах. Поэтому буква «а» встречается со средней частотой 200/1000=0,2; Вероятность появления буквы “а” в тексте (p _a )можем считать приблизительно равной 0,2;

буква «ф» встречается с частотой 2/1000=0,002; буква «р» — с частотой 40/1000=0,04;

Аналогично, p _р = 0,04, p _ф = 0,002. Далее поступаем согласно К.Шеннону. Берем двоичный логарифм от величины 0,2 и называем то, что получилось количеством информации, которую переносит одна-единственная буква “а” в рассматриваемом тексте. Точно такую же операцию проделаем для каждой буквы. Тогда количество собственной информации, переносимой одной буквой равно log ₂ 1/p _i = — log ₂ p _i , Удобнее в качестве меры количества информации пользоваться средним значением количества информации, приходящейся на один символ алфавита

I _ср = —

Значение I _ср достигает максимума при равновероятных событиях, то есть при равенстве всех p _i

В этом случае формула Шеннона превращается в формулу Хартли.

При составлении таблицы мы должны учитывать:

Ввод данных (что дано в условии).

Подсчет общего количества числа возможных исходов (формула N=K ₁ +K ₂ +…+K _i ).

Подсчет вероятности каждого события (формула p _i = К _i /N).

Подсчет количества информации о каждом происходящем событии (формула I _i = log ₂ (1/p _i )).

Подсчет количества информации для событий с различными вероятностями (формула Шеннона).

1 . Сделать табличную модель для вычисления количества информации.

2 . Используя табличную модель, сделать вычисления к задаче №2 (рис.3), результат вычисления занести в тетрадь.

3 . Используя таблицу-шаблон, решить задачи №3,4 (рис.4, рис.5), решение оформить в тетради.

В классе 30 человек. За контрольную работу по информатике получено 15 пятерок, 6 четверок, 8 троек и 1 двойка. Какое количество информации несет сообщение о том, что Андреев получил пятерку?

В коробке лежат кубики: 10 красных, 8 зеленых, 5 желтых, 12 синих. Вычислите вероятность доставания кубика каждого цвета и количество информации, которое при этом будет получено.

В непрозрачном мешочке хранятся 10 белых, 20 красных, 30 синих и 40 зеленых шариков. Какое количество информации будет содержать зрительное сообщение о цвете вынутого шарика?

Алфавитный подход к оценке количества информации. Формула Хартли

Вы будете перенаправлены на Автор24

Содержательный подход к оценке количества информации, который мы рассматривали ранее, измеряет ее количество, как уменьшение неопределенности наших знаний.

Однако любое техническое устройство не способно воспринимать непосредственно содержание информации, оно лишь понимает наличие или отсутствие электрических сигналов. Вследствие чего в вычислительной технике вынуждены использовать другой подход к оценке количества информации, который называется алфавитным.

Принцип алфавитного подхода к оценке количества информации

Алфавитный подход строится на принципе, утверждающем, что любое сообщение можно представить в виде кодов с помощью конечной последовательности символов, содержащейся в любом алфавите. Носители информации содержат любые последовательности символов, которые могут храниться, передаваться и обрабатываться как с помощью человека, так и с помощью технических устройств, в частности компьютера. Этот подход описал А.Н. Колмогоров, согласно которому, информативность, заключающаяся в последовательности символов, не может зависеть от содержания самого сообщения, а может определяться лишь минимальным количеством символов, необходимых для ее кодирования. Подобный подход к оценке количества информации носит объективный характер, так как не зависит от получателя, принимающего сообщения. Смысл же сообщений может учитываться только на этапе выбора алфавита кодирования либо не учитываться совсем.

В основу принципа этого подхода лег подсчет числа символов в сообщении, таким образом, важна только длина сообщения и совсем не учитывается его содержание. Однако на длину сообщения может влиять мощность алфавита используемого языка.

Самый простой способ разобраться в этом — рассмотреть пример любого текста, написанного на каком-нибудь языке. Для нас, конечно же, удобным будет текст на русском языке.

Мощность алфавита и информационная емкость. Формула Хартли

Все множество символов, из которых состоит язык, можно традиционно назвать алфавитом. Как правило, под алфавитом понимаются только буквы, но кроме них при написании текстов используются знаки препинания, цифры, скобки, пробелы, их тоже, в свою очередь, можно включить в алфавит.

Таким образом, алфавит — это множество символов, используемых при записи текста.

Мощность (размер) алфавита — это полное количество символов в алфавите.

Мощность алфавита обозначается буквой $N$.

Например:

мощность алфавита, состоящего из русских букв (кириллицы), равна $33$;

мощность алфавита, состоящего из латинских букв — $26$;

мощность алфавита текста набранного с клавиатуры компьютера равна $256$ (строчные и прописные латинские и русские буквы, цифры, знаки арифметических операций, скобки, знаки препинания и т.д.);

мощность двоичного алфавита равна $2$.

Готовые работы на аналогичную тему

При алфавитном подходе считают, что каждый символ текста несет в себе определенную информационную емкость, которая, в свою очередь, зависит от мощности алфавита.

Алфавит, с помощью которого записывается сообщение, состоит из $N$ знаков. В самом простом случае при длине кода сообщения, равной одному знаку, отправитель может послать одно из $N$ возможных сообщений, которое будет нести количество информации, равное $I$, согласно формуле:

где $N$ — количество знаков в алфавите знаковой системы,

$I$ — количество информации, которое несет каждый знак.

Данную формулу вывел Р. Хартли, который в $20$-е годы прошлого столетия заложил основы теории информации, в которой определялась мера количества информации при решении некоторых задач.

Хартли утверждал, что на количество информации, содержащейся в сообщении, может влиять фактор неожиданности, который, в свою очередь, зависит от вероятности получения сообщения. Если эта вероятность получения сообщения высокая, а неожиданность при этом низкая, то сообщение будет содержать мало полезной для человека информации.

Однако при создании своей формулы Р.Хартли полностью исключил фактор неожиданности. Формула Хартли работает только в том случае, когда появление символов равновероятно и они статистически независимы.

Например, с помощью приведенной формулы можно определить количество информации, которое несет знак в двоичной системе счисления:

Информационная емкость знака двоичной системы составляет 1 бит.

Необходимо определить информационную емкость буквы русского алфавита (без учета буквы «ё»).

Решение:

Представим себе, что текст к нам поступает последовательно, по одному знаку, словно бумажная лента, выползающая из телеграфного аппарата. Предположим, что каждый символ, который появляется на ленте, с равной вероятностью может быть любым символом алфавита. В действительности это не совсем так, но для упрощения примем такое предположение.

В каждой очередной позиции текста может появиться любой из $N$ символов. Тогда, согласно известной нам формуле, каждый такой символ несет количество информации равное $I$ бит, которое можно определить из решения уравнения:

Информационная емкость буквы русского алфавита составляет $5$ бит информации.

Таким образом, формула определения $N$ связывает между собой количество возможных событий и количество информации, которое содержит в себе полученное сообщение. В рассматриваемой выше задаче $N$ — это количество знаков в русском алфавите, а $I$ — количество информации, которое несёт одна буква.

Сообщение состоит из последовательности знаков, каждый из которых несет определенное количество информации.

Количество информации в сообщении можно определить, используя формулу:

где $I_c$ — количество информации, содержащееся в сообщении;

$I$ — количество информации, которое несет один знак (информационная емкость);

$K$ — количество знаков в сообщении.

Рассмотрим пример решения задачи

Необходимо определить какое количество информации содержит слово «Привет», если считать, что алфавит состоит из $32$ букв (без учета буквы «ё»)?

Решение. Чтобы решить задачу, для начала определим количество знаков в сообщении и мощность используемого алфавита.

Количество знаков в сообщении: $K= 6$,

а мощность данного алфавита: $N = 32$.

Необходимо определить какое количество информации содержит слово «Привет».

Для этого необходимо умножить количество информации, которое несет один знак ($I$), на количество знаков в сообщении ($K$), т.е. воспользоваться формулой: $I_c = K \cdot I$.

Однако мы не сможем воспользоваться этой формулой, поскольку нам не известно какое количество информации несет один знак ($I$).

Для решения задачи воспользуемся формулой Хартли. Сообщение записано с помощью алфавита, мощность которого равна $32$, т.е. $N = 32$.

Решив уравнение, используя формулу $N = 2^I$, мы получили, что количество информации $I = 5$ бит. Зная количество информации, которое содержит в себе один знак нашего алфавита, и количество знаков в сообщении, можно определить, какое количество информации содержит наше сообщение.

Итак: $I_c = K \cdot I = 6 \cdot 5 = 30$ бит.

При измерении информации удобным является использование размера алфавита $N$, равного целой степени двойки. К примеру, если $N=16$, то это означает, что каждый символ несет $4$ бита информации, так как $2^4= 16$.

Единицы измерения информации

Ограничений максимального размера алфавита теоретически не существует. Однако существует алфавит, который можно назвать достаточным. Он используется при работе с компьютером. Мощность этого алфавита — $256$ символов. Он включает в себя практически все необходимые символы: латинские и русские буквы, цифры, знаки арифметических операций, всевозможные скобки, знаки препинания.

Поскольку $256 = 2^8$, то отсюда следует, что $1$ символ этого алфавита содержит $8$ бит информации. Эта величина лежит в основе использования вычислительной технике и носит название — байт.

Используя данный алфавит, который еще называется таблицей ASCII-кодов, можно легко подсчитать объем информации в тексте. В данном случае $1$ символ алфавита содержит в себе $1$ байт информации, поэтому необходимо просто определить количество символов, то число, которое получим в результате, и будет выражать информационный объем текста в байтах.

Допустим небольшая книга, распечатанная на принтере, содержит $50$ страниц, при этом на каждой странице расположено $50$ строк, в каждой строке — $60$ символов.

Проведем несложный расчет и получим, что страница содержит:

$50 \cdot 60 = 3000$ байт информации.

Объем же информации, содержащейся в книге:

$3000 \cdot 50 = 150 \ 000$ байт.

Любая система единиц измерения содержит основные единицы и производные от них.

При измерении больших объемов информации на практике широко используются следующие производные от байта единицы, которые приведены в таблице: