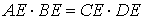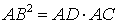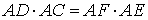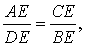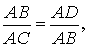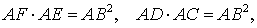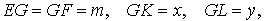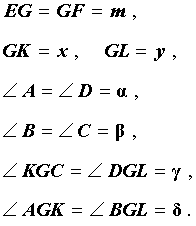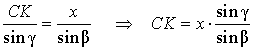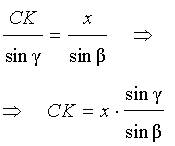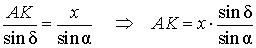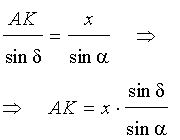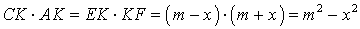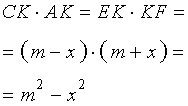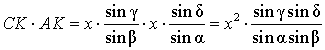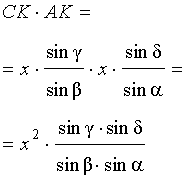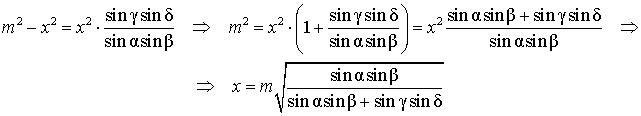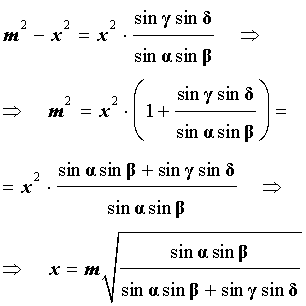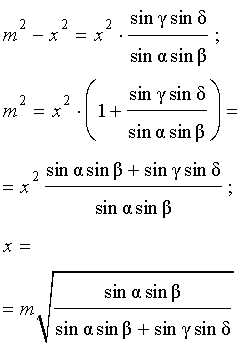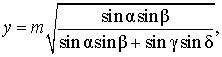Уравнение хорды окружности делящейся точкой пополам
Глава 22. Диаметры линий второго порядка
В курсе аналитической геометрии доказывается, что середины параллельных хорд линии второго порядка лежат на одной прямой. Эта прямая называется диаметром линии второго порядка. Диаметр, делящий пополам какую-нибудь хорду (а значит, и все параллельные ей), называется сопряженным этой хорде (и всем хордам, который ей параллельны). Все диаметры эллипса и гиперболы проходят через центр. Если эллипс задан уравнением
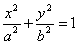
то его диаметр, сопряженный хордам с угловым коэффициентом k , определяется уравнением
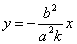
Если гипербола задана уравнением
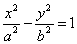
то ее диаметр, сопряженный хордам с угловым коэффициентом k , определяется уравнением
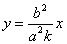
Все диаметры параболы параллельны ее оси. Если парабола задана уравнением
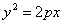
то ее диаметр, сопряженный хордам с угловым коэффициентом k , определяется уравнением
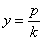
Если один из двух диаметров эллипса или гиперболы делит пополам хорды, параллельные другому, то второй диаметр делит пополам хорды, параллельные первому. Такие два диаметра называются взаимно сопряженными.
Если k и k ’ — угловые коэффициенты двух взаимно сопряженных диаметров эллипса (1), то
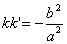
Если k и k ’ — угловые коэффициенты дух взаимно сопряженных диаметров гиперболы (2), то
Соотношения (3) и (4) называются условиями сопряженности диаметров соответственно для эллипса и для гиперболы.
Диаметр линии второго порядка, перпендикулярный к сопряженным хордам, называется главным.
Отрезки и прямые, связанные с окружностью. Теорема о бабочке
 Отрезки и прямые, связанные с окружностью Отрезки и прямые, связанные с окружностью |
 Свойства хорд и дуг окружности Свойства хорд и дуг окружности |
 Теоремы о длинах хорд, касательных и секущих Теоремы о длинах хорд, касательных и секущих |
 Доказательства теорем о длинах хорд, касательных и секущих Доказательства теорем о длинах хорд, касательных и секущих |
 Теорема о бабочке Теорема о бабочке |
Отрезки и прямые, связанные с окружностью
| Фигура | Рисунок | Определение и свойства | ||||||||||||||||||||||||||
| Окружность |  | |||||||||||||||||||||||||||
| Круг |  | |||||||||||||||||||||||||||
| Радиус |  | |||||||||||||||||||||||||||
| Хорда |  | |||||||||||||||||||||||||||
| Диаметр |  | |||||||||||||||||||||||||||
| Касательная |  | |||||||||||||||||||||||||||
| Секущая |  | |||||||||||||||||||||||||||
| Окружность |
 |
Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности

Конечная часть плоскости, ограниченная окружностью

Отрезок, соединяющий центр окружности с любой точкой окружности

Отрезок, соединяющий две любые точки окружности

Хорда, проходящая через центр окружности.
Диаметр является самой длинной хордой окружности

Прямая, имеющая с окружностью только одну общую точку.
Касательная перпендикулярна к радиусу окружности, проведённому в точку касания

Прямая, пересекающая окружность в двух точках
Свойства хорд и дуг окружности
| Фигура | Рисунок | Свойство |
| Диаметр, перпендикулярный к хорде | 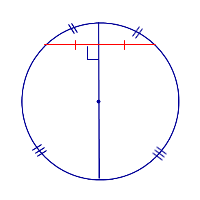 | Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею две дуги пополам. |
| Диаметр, проходящий через середину хорды | Диаметр, проходящий через середину хорды, перпендикулярен к этой хорде и делит стягиваемые ею две дуги пополам. | |
| Равные хорды | 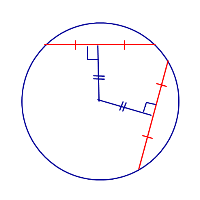 | Если хорды равны, то они находятся на одном и том же расстоянии от центра окружности. |
| Хорды, равноудалённые от центра окружности | Если хорды равноудалены (находятся на одном и том же расстоянии) от центра окружности, то они равны. | |
| Две хорды разной длины | 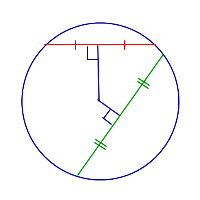 | Большая из двух хорд расположена ближе к центру окружности. |
| Равные дуги | 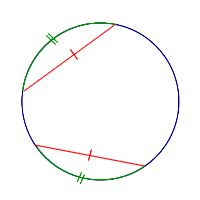 | У равных дуг равны и хорды. |
| Параллельные хорды | 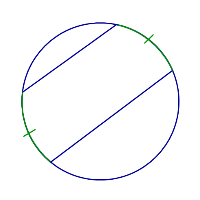 | Дуги, заключённые между параллельными хордами, равны. |
| Диаметр, перпендикулярный к хорде |
 |
Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею две дуги пополам.

Диаметр, проходящий через середину хорды, перпендикулярен к этой хорде и делит стягиваемые ею две дуги пополам.

Если хорды равны, то они находятся на одном и том же расстоянии от центра окружности.

Если хорды равноудалены (находятся на одном и том же расстоянии) от центра окружности, то они равны.

Большая из двух хорд расположена ближе к центру окружности.

У равных дуг равны и хорды.

Дуги, заключённые между параллельными хордами, равны.
Теоремы о длинах хорд, касательных и секущих
| Фигура | Рисунок | Теорема | ||||||||||||||||
| Пересекающиеся хорды | 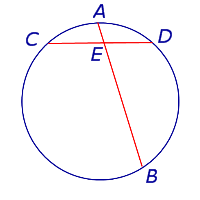 | |||||||||||||||||
| Касательные, проведённые к окружности из одной точки | 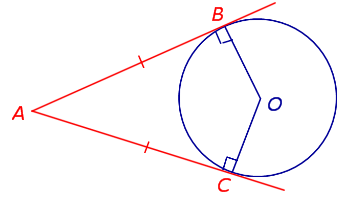 | |||||||||||||||||
| Касательная и секущая, проведённые к окружности из одной точки | 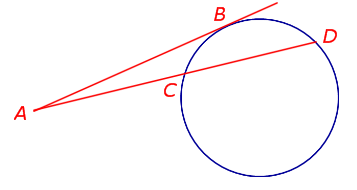 | |||||||||||||||||
| Секущие, проведённые из одной точки вне круга | 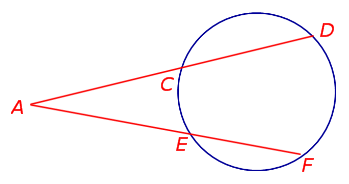 | |||||||||||||||||
| Пересекающиеся хорды | ||
 | ||
| Касательные, проведённые к окружности из одной точки | ||
 | ||
| Касательная и секущая, проведённые к окружности из одной точки | ||
 | ||
| Секущие, проведённые из одной точки вне круга | ||
 | ||
| Пересекающиеся хорды |
 |
Произведения длин отрезков, на которые разбита каждая из хорд, равны:
Если к окружности из одной точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны.
Доказательства теорем о длинах хорд, касательных и секущих
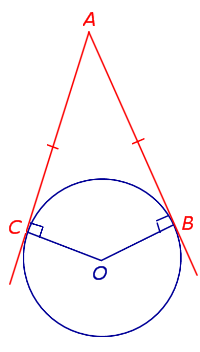
Теорема 1 . Предположим, что хорды окружности AB и CD пересекаются в точке E (рис.1).
Тогда справедливо равенство
Доказательство . Заметим, что углы BCD и BAD равны как вписанные углы, опирающиеся на одну и ту же дугу. Углы BEC и AED равны как вертикальные. Поэтому треугольники BEC и AED подобны. Следовательно, справедливо равенство
откуда и вытекает требуемое утверждение.
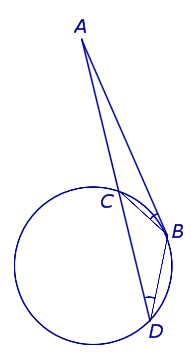
Теорема 2 . Предположим, что из точки A , лежащей вне круга, к окружности проведены касательная AB и секущая AD (рис.2).
Точка B – точка касания с окружностью, точка C – вторая точка пересечения прямой AD с окружностью. Тогда справедливо равенство
Доказательство . Заметим, что угол ABC образован касательной AB и хордой BC , проходящей через точку касания B . Поэтому величина угла ABC равна половине угловой величины дуги BC . Поскольку угол BDC является вписанным углом, то величина угла BDC также равна половине угловой величины дуги BC . Следовательно, треугольники ABC и ABD подобны (угол A является общим, углы ABC и BDA равны). Поэтому справедливо равенство
откуда и вытекает требуемое утверждение.
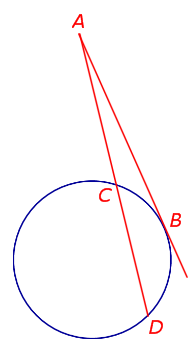
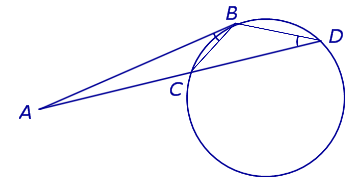
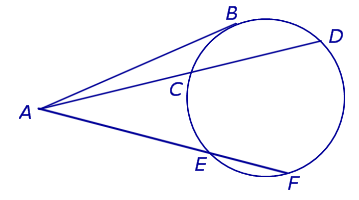
Теорема 3 . Предположим, что из точки A , лежащей вне круга, к окружности проведены секущие AD и AF (рис.3).
Точки C и E – вторые точки пересечения секущих с окружностью. Тогда справедливо равенство
Доказательство . Проведём из точки A касательную AB к окружности (рис. 4).
Точка B – точка касания. В силу теоремы 2 справедливы равенства
откуда и вытекает требуемое утверждение.
Теорема о бабочке
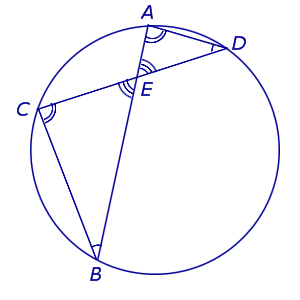
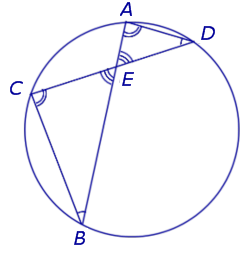
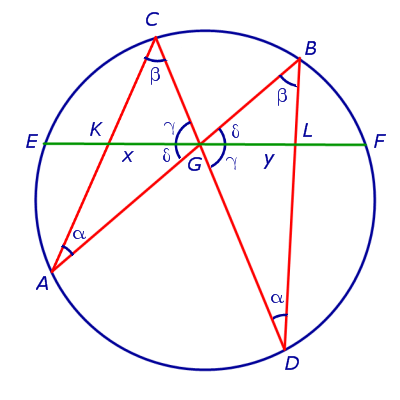
Теорема о бабочке . Через середину G хорды EF некоторой окружности проведены две произвольные хорды AB и CD этой окружности. Точки K и L – точки пересечения хорд AC и BD с хордой EF соответственно (рис.5). Тогда отрезки GK и GL равны.
Доказательство . Существует много доказательств этой теоремы. Изложим доказательство, основанное на теореме синусов, которое, на наш взгляд, является наиболее наглядным. Для этого заметим сначала, что вписанные углы A и D равны, поскольку опираются на одну и ту же дугу. По той же причине равны и вписанные углы C и B . Теперь введём следующие обозначения:
Воспользовавшись теоремой синусов, применённой к треугольнику CKG , получим
Воспользовавшись теоремой синусов, применённой к треугольнику AKG , получим
Воспользовавшись теоремой 1, получим
Воспользовавшись равенствами (1) и (2), получим
Проводя совершенно аналогичные рассуждения для треугольников BGL и DGL , получим равенство
откуда вытекает равенство
что и завершает доказательство теоремы о бабочке.
Задачи для самостоятельного решения. 1 Составить уравнение хорды окружности х2+у2 = 49, делящейся в точке А(1;2) пополам
1 Составить уравнение хорды окружности х 2 +у 2 = 49, делящейся в точке А(1;2) пополам.
Ответ.х + 2у -5 = 0.
2. Определить координаты центров и радиусы окружностей:
Ответ: а) а = 4, b=-3, r= 5; б) а = -5, b = 2, r=0. Уравнение определяет точку;
в) а =2, b=-7, r 2 =-1. Уравнение не имеет геометрического смысла (мнимая, окружность).
3. Найти угол между радиусами окружности
х 2 +у 2 +4х-6у=0, проведенными в точки пересечения ее с осью Оу.
Ответ: tgφ=-2,4.
4. Составить уравнение окружности, проходящей через точки А(1; 2), В(0;-1), С(-3; 0).
Ответ: (х+1) 2 +(у -1) 2 =5.
5. Составить уравнение окружности, проходящей через точки А (7; 7) и В(-2; 4), зная, что ее центр лежит на прямой
Ответ: (х— З) 2 +(у-4) 2 =25.
6. Составить уравнение общей хорды окружностей х 2 +у 2 =16 и (х -5) 2 + у 2 = 9.
Ответ: х=3,2.
7. Составить уравнение прямой, проходящей через левый фокус и нижнюю вершину эллипса 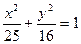
Ответ: 4х+3у+12= 0.
8. На прямой х+5=0 найти точку, одинаково удаленную от левого фокуса и верхней вершины эллипса 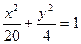
Ответ: М(—5; 7).
9. Пользуясь определением эллипса, составить его уравнение, зная, что точки F1 (0; 0) и F2 (1; 1) являются фокусами эллипса, а длина большой оси равна 2.
Ответ: Зх 2 + Зу 2 — 2ху — 2х — 2у — 1 == 0.
10. Составить уравнение геометрического места точек, расстояния которых от точки А (0; 1) з два раза меньше расстояния до прямой у—4=0.
Ответ: 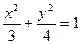
Занятие 16. Кривые второго порядка: гипербола, парабола
Гипербола.
Гиперболой называется геометрическое место точек, абсолютная величина разности расстояний которых до двух данных точек, называемых фокусами, есть величина постоянная (её обозначают через 2а), причем эта постоянная меньше расстояния между фокусами. Поместив фокусы гиперболы в точках F1(с; 0) и F2(-с;0), получаем уравнение гиперболы в виде 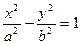

это простейшее (каноническое) уравнение гиперболы. Гипербола состоит из двух ветвей и расположена симметрично относительно осей координат. Точки А1(а;0) и А2(-а;0) называются вершинами гиперболы.
Отрезок А1А2=2а называют вещественной осью гиперболы, а отрезок В1В2=2b – мнимой осью (рис. 15).
Прямая называется асимптотой гиперболы, если расстояние точки гиперболы М (х;у) от этой прямой стремится к нулю при х→+∞ или х→-∞. Гипербола имеет две асимптоты, уравнения которых 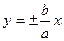
х = — а, у=b, у=-b. Прямые, проходящие через противоположные вершины этого прямоугольника, являются асимптотами гиперболы. На чертеже указано взаимное расположение гиперболы и ее асимптот. Отношение ε 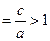
Если а=b, то уравнение гиперболы принимает вид
Такая гипербола называется равнобочной.

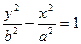
также является уравнением гиперболы, но вещественной осью этой гиперболы служит отрезок оси Оу длины 2b.
Две гиперболы 
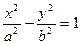
Пример 16.1.Эксцентриситет гиперболы равен 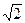
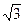
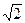
Решение. По определению эксцентриситета можем написать равенство 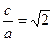
Другое равенство имеем из условия нахождения точки М на гиперболе, т. е. 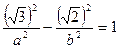
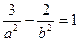
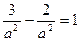
Таким образом, уравнение искомой гиперболы имеет вид х 2 — у 2 =1.
Парабола.
Параболой называется геометрическое место точек, равноудаленных от данной точки, называемой фокусом, и данной прямой, называемой директрисой. Если директрисой параболы 
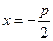
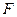
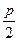

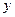

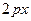
Эта парабола расположена симметрично относительно оси абсцисс (рис.6, где р 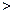
Уравнение

является уравнение параболы, симметричной относительно оси ординат. При p>0 параболы (16.1) и (16.2) обращены в положительную сторону соответствующей оси, а при p
Решение. Поскольку известны длина хорды и расстояние ее от вершины, то, следовательно , известны координаты конца этой хорды-точки М, лежащей на параболе. Уравнение параболы имеет вид 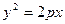

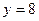
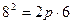

Таким образом, уравнение искомой параболы 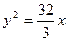
Пример 16.3. Составить уравнение параболы с вершиной в начале координат, симметричной относительно оси Оу и отсекающей на биссектрисе 

Решение. Искомое уравнение параболы 

Длина хорды определяется как расстояние между двумя точками 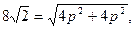
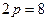

http://www.resolventa.ru/demo/training.htm
http://lektsii.org/3-113924.html