Уравнение и его корни видеоурок

Решение уравнений

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

На данном уроке подробно рассмотрены способы решения уравнений. Объяснены способы решения уравнений, как методом подбора, так и с учетом взаимосвязи компонентов действий сложения и вычитания.

Если у вас возникнет сложность в понимании темы, рекомендуем посмотреть урок «Уравнения и неравенства».

Урок «Уравнения и его корни»

Краткое описание документа:

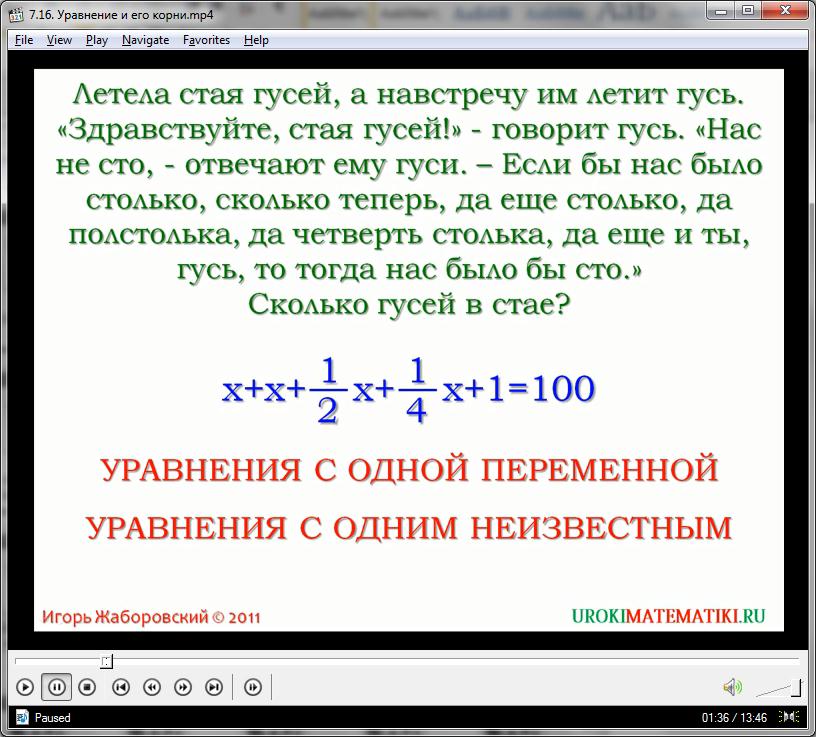
В предложенном видео речь идет о понятии уравнения и его корнях. Для начала рассмотрена задача о гусях. В задаче стая гусей отвечает гусю, что если бы их было столько, сколько сейчас, да еще столько, да еще полстолька, да еще четверть столько, да еще он, то их было бы сто гусей. Вопрос: Сколько гусей в стае?

Неизвестное число гусей в стае обозначили через Х.

В результате получили: Х + Х +1/2Х+ 1/4Х + 1 = 100.

В этом равенстве присутствует неизвестная нам величина Х, значение которой мы ищем. Это значение мы можем найти из составленного нами равенства. Подобные равенства называют уравнениями с одной переменной, или уравнениями с одним неизвестным.

Искомую неизвестную величину принято обозначать буквой Х, хотя можно обозначать любой буквой. Впервые неизвестную величину обозначил буквой и составил уравнение в явном виде с неизвестным древнегреческий математик Диофант в своем труде «Арифметика».

В составленном уравнении необходимо найти такое значение переменной, которое превращает уравнение в правильное числовое равенство. Такое значение неизвестной называют корнем уравнения.

Делаем вывод, что корнем уравнения называется значение переменной, превращающее уравнение в верное числовое равенство. Решить уравнение означает найти множество его корней, число которых может быть различным. Корень может быть один, их может быть несколько, а может и не быть ни одного. В конечном итоге, чтобы решить уравнение, необходимо определить все его корни или убедиться, что у уравнения нет корней.

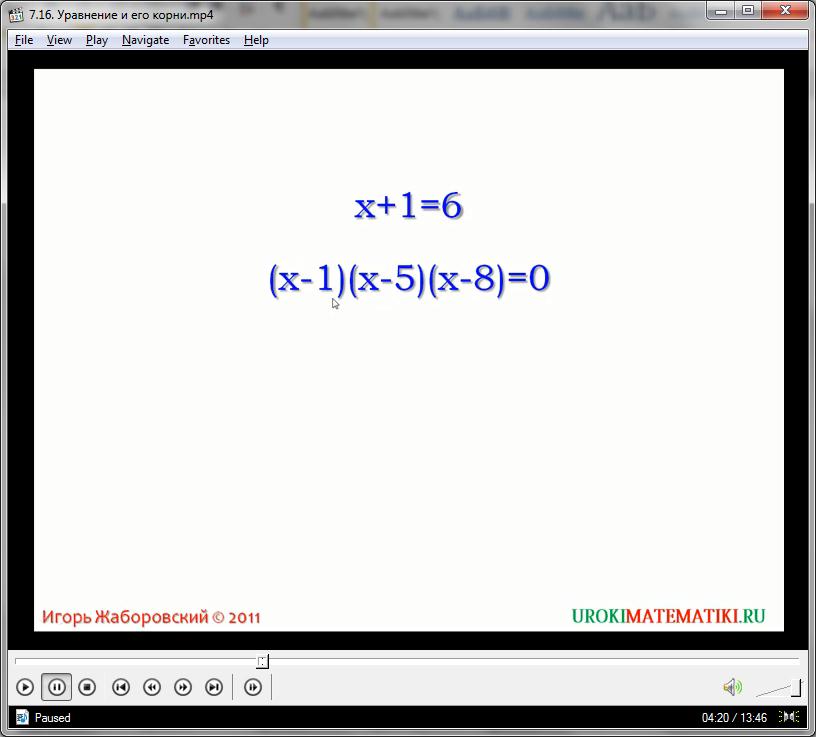
Количество корней уравнения может быть разным в зависимости от вида уравнения. В некоторых случаях и число может быть бесконечным, а может быть равно нулю. Для убедительности автор предлагает рассмотреть примеры уравнений, которые имеют разное количество корней. Это уравнения Х + 1 = 6, (Х – 1)(Х – 5)(Х – 8) = 0, Х = Х + 4, 3(Х + 5) = 3Х + 15. В первом случае корень один, так как только в случае, когда Х = 5, уравнение становится верным числовым равенством 6 = 6. Второе уравнение имеет три корня. Это числа 1, 5, 8. Именно при этих значениях переменной выражения в скобках по очереди принимают значение 0. При умножении на 0 все выражение становиться равным 0. Получаем равенство 0 = 0. Третье уравнение не имеет корней, потому что при любом значении Х правая часть принимает значение больше, чем левая. Четвертое уравнение в свою очередь имеет бесконечное число корней в силу применения сочетательного свойства умножения. После раскрытия скобок и левая, и правая части уравнения имеют одинаковый вид: 3Х + 15 = 3Х = 15.

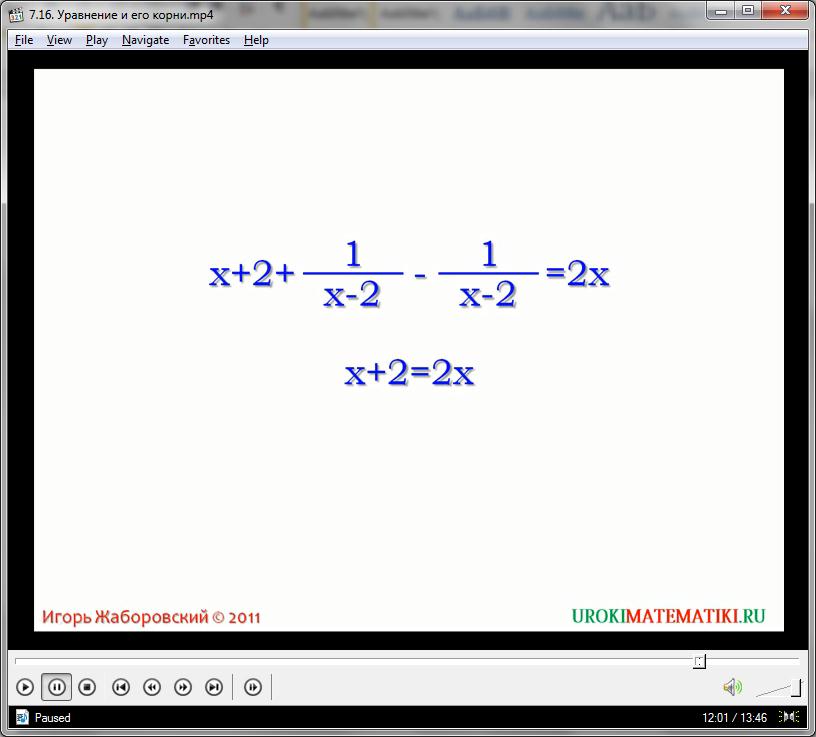
Далее автор вводит понятие допустимых значений неизвестного. Для этого рассматриваются уравнения 17 – 3Х = 2Х – 2 и (25 – Х)/(Х – 2) = Х + 9. Если в первом случае неизвестное Х может принимать любые значения, то во втором при Х = 2 получаем деление на 0. Следовательно, значения переменной, которые можно подставлять в уравнение в первом случае все числа, а во втором – все числа, кроме 2.

Область определения уравнения – это множество значений переменно, при которых обе части уравнения имеют смысл.

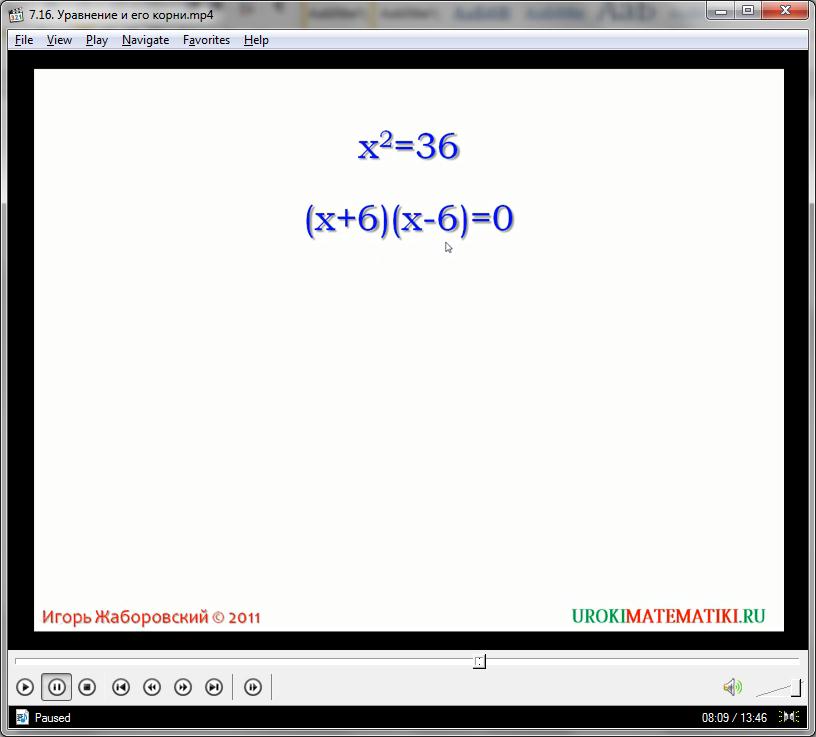
После этого вводится понятие равносильности уравнений. Рассматриваются уравнения Х 2 = 36 и (Х – 6)(Х + 6) = 0. У этих уравнений одинаковые корни; такие уравнения принято называть равносильными.

При решении уравнений их заменяют равносильными уравнениями, но более простыми по форме. Необходимо помнить некоторые правила замены уравнения на равносильное уравнение. Во время переноса слагаемого через знак равенства знак слагаемого меняем на противоположный. При умножении или делении обеих частей уравнения на одно и то же число, неравное 0, уравнение останется равносильным. Можно выполнять тождественные преобразования, если они не влияют на область определения уравнения.

Уравнение и его корни видеоурок

УРАВНЕНИЕ И ЕГО КОРНИ

Решим задачу: «На двух полках 40 книг, причем на верхней полке в 8 раза больше книг, чем на нижней. Сколько книг на нижней полке?»

Обозначим буквой х число книг на нижней полке. Тогда число книг на верхней полке равно Зх. По условию задачи на обеих полках находится 40 книг. Это условие можно записать в виде равенства:

3x + x = 40.

Чтобы найти неизвестное число книг, мы составили равенство, содержащее переменную. Такие равенства называют уравнениями. Переменную в уравнении называют также неизвестным числом или просто неизвестным.

Нам надо найти число, при подстановке которого вместо х в уравнение Зх + х = 40 получается верное равенство. Такое число называют решением уравнения или корнем уравнения. Равенство Зх + х = 40 верно при х = 10. Число 10 — корень уравнения Зх + х = 40.

Определение. Корнем уравнения называется значение переменной, при котором уравнение обращается в верное равенство.

Уравнение Зх + х = 40 имеет один корень. Можно привести примеры уравнений, которые имеют два, три и более корней или вообще не имеют корней.

Так, уравнение (х—4)(х — 5) (х—6)=0 имеет три корня: 4, б и 6. Действительно, каждое из этих чисел обращает в нуль один из множителей произведения (х—4) (х—5)(х—б), а значит, и само произведение. При любом другом значении х ни один из множителей в нуль не обращается, а значит, не обращается в нуль и произведение. Уравнение х + 2 = х не имеет корней, так как при любом значении х левая часть уравнения на 2 больше правой части.

Решить уравнение — значит найти все его корни или доказать, что их нет.

Уравнение х 2 =4 имеет два корня — числа 2 и —2. Уравнение (х—2) (х+2)=0 также имеет корни 2 и —2. Уравнения, имеющие одни и те же корни, называют равносильными уравнениями. Уравнения, не имеющие корней, также считают равносильными.

Уравнения обладают следующими свойствами:

1) если к обеим частям уравнения прибавить одно и то же число, то получится уравнение, равносильное данному;

2) если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получится уравнение, равносильное данному.

Рассмотрим уравнение х 2 — 2 = 7. Прибавив к левой и правой частям этого уравнения число 2, получим уравнение х 2 = 9. Докажем, что уравнения х 2 — 2 = 7 и х 2 = 9 равносильны.

Пусть некоторое значение х является корнем первого уравнения, т. е. при этом значении- х уравнение х 2 —2 = 7 обращается в верное равенство. Прибавив к обеим частям этого равенства число 2, мы снова получим верное равенство. Значит, при этом значении х второе уравнение также обращается в верное равенство. Мы доказали, что каждый корень первого уравнения является корнем второго уравнения.

Допустим теперь, что некоторое значение х является корнем второго уравнения х 2 = 9, т. е. обращает его в верное равенство. После вычитания из обеих частей этого равенства числа 2 мы получим верное равенство. Значит, при этом значении х первое уравнение также обращается в верное равенство. Поэтому каждый корень второго уравнения является корнем первого.

Таким образом, уравнения х 2 — 2 = 7 и х 2 = 9 имеют одни и те же корни, т. е. являются равносильными.

Подобными рассуждениями устанавливается справедливость обоих свойств уравнений в общем случае.

3) Можно также доказать, что если в уравнении перенести слагаемое ив одной части в другую, изменив его знак, то получится уравнение, равносильное данному. Например, перенеся в уравнении 5х = 2х + 9 слагаемое 2х с противоположным знаком из правой части уравнения в левую, получим уравнение 5х—2дс=9, ему равносильное.

Перенос слагаемых из одной части уравнения в другую часто применяется при решении уравнений.

ЛИНЕЙНОЕ УРАВНЕНИЕ С ОДНОЙ ПЕРЕМЕННОЙ

Каждое из уравнений 5х = — 4, — 0,2х = 0, —х= —6,5 имеет вид ах = b где а и b — числа. В первом уравнении а = 5, b= — 4, во втором а= —0,2, b = 0, в третьем а= — 1, b= —6,5. Такие уравнения называют линейными уравнениями с одной переменной.

Определение. Уравнение вида ах = b, где х — переменная, а и b — числа, называется линейным уравнением с одной переменной.

Число а называется коэффициентом при переменной, а число b — свободным членом.

Рассмотрим линейное уравнение ах = b, в котором коэффициент а не равен нулю. Разделив обе части уравнения на а, получим . Значит, линейное уравнение ах=b в котором а≠ 0, имеет единственный корень

Рассмотрим теперь линейное уравнение ах = b, у которого коэффициент а равен нулю. Если а = 0 и b≠ О, то уравнение ах =b не имеет корней, так как равенство Ox = b, где b≠ 0, не является верным ни при каком x. Если а = 0 и b = О, то любое значение х является корнем уравнения, так как равенство 0х = 0 верно при любом х.

Решение многих уравнений сводится к решению линейных уравнений.

Пример. Решим уравнение

Перенесем слагаемое —х в левую часть уравнения, а слагаемое 28 в правую, изменив при этом их знаки:

Приведем подобные слагаемые:

Заменяя последовательно одно уравнение другим, равносильным ему, мы получили линейное уравнение, в котором коэффициент при х отличен от нуля. Разделим обе части уравнения на этот коэффициент:

Число —5 является корнем уравнения .

Может случиться, Что при решении уравнения мы придем к линейному уравнению вида 0х=b. В этом случае исходное уравнение либо не имеет корней, либо его корнем является любое число. Например, уравнение сводится к уравнению Ох = 7, и, значит, оно не имеет корней. Уравнение сводится к уравнению 0х = 0, и, значит, любое число является его корнем.