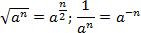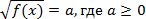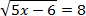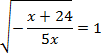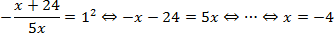Задача B7 — логарифмические, показательные и иррациональные уравнения
Все задачи B7, которые мне доводилось видеть, были сформулированы примерно одинаково: решить уравнение. При этом сами уравнения относятся к одному из трех видов:
- Логарифмические;
- Показательные;
- Иррациональные.
Вообще говоря, полноценное руководство по каждому типу уравнений займет не один десяток страниц, выходя далеко за рамки ЕГЭ. Поэтому мы рассмотрим лишь самые простые случаи, требующие незатейливых рассуждений и выкладок. Этих знаний будет вполне достаточно, чтобы решить любую задачу B7.
В математике термин «решить уравнение» означает найти множество всех корней данного уравнения, либо доказать, что это множество пусто. Но в бланк ЕГЭ можно вписывать только числа — никаких множеств. Поэтому, если в задании B7 оказалось больше одного корня (или, наоборот, ни одного) — в решении была допущена ошибка.
Логарифмические уравнения
— это любое уравнение, которое сводится к виду log a f ( x ) = k , где a > 0, a ≠ 1 — основание логарифма, f ( x ) — произвольная функция, k — некоторая постоянная.
Такое уравнение решается внесением постоянной k под знак логарифма: k = log a a k . Основание нового логарифма равно основанию исходного. Получим уравнение log a f ( x ) = log a a k , которое решается отбрасыванием логарифма.
Заметим, что по условию a > 0, поэтому f ( x ) = a k > 0, т.е. исходный логарифм существует.
Решение. log7 (8 − x ) = 2 ⇔ log7 (8 − x ) = log7 7 2 ⇔ 8 − x = 49 ⇔ x = −41.
Решение. log0,5 (6 − x ) = −2 ⇔ log0,5 (6 − x ) = log0,5 0,5 −2 ⇔ 6 − x = 4 ⇔ x = 2.
Но что делать, если исходное уравнение окажется сложнее, чем стандартное log a f ( x ) = k ? Тогда сводим его к стандартному, собирая все логарифмы в одной стороне, а числа — в другой.
Если в исходном уравнении присутствует более одного логарифма, придется искать область допустимых значений (ОДЗ) каждой функции, стоящей под логарифмом. Иначе могут появиться лишние корни.
Поскольку в уравнении присутствуют два логарифма, найдем ОДЗ:
- x + 1 > 0 ⇔ x > −1
- x + 5 > 0 ⇔ x > −5
Получаем, что ОДЗ — это интервал (−1, +∞). Теперь решаем уравнение:
log5 ( x + 1) + log5 ( x + 5) = 1 ⇒ log5 ( x + 1)( x + 5) = 1 ⇔ log5 ( x + 1)( x + 5) = log5 5 1 ⇔ ( x + 1)( x + 5) = 5 ⇔ x 2 + 6 x + 5 = 5 ⇔ x ( x + 6) = 0 ⇔ x 1 = 0, x 2 = −6.
Но x 2 = −6 не подходит по ОДЗ. Остается корень x 1 = 0.
Показательные уравнения
— это любое уравнение, которое сводится к виду a f ( x ) = k , где a > 0, a ≠ 1 — основание степени, f ( x ) — произвольная функция, k — некоторая постоянная.
Это определение почти дословно повторяет определение логарифмического уравнения. Решаются показательные уравнения даже проще, чем логарифмические, ведь здесь не требуется, чтобы функция f ( x ) была положительна.
Для решения сделаем замену k = a t , где t — вообще говоря, логарифм ( t = log a k ), но в ЕГЭ числа a и k будут подобраны так, что найти t будет легко. В полученном уравнении a f ( x ) = a t основания равны, а значит, равны и показатели, т.е. f ( x ) = t . Решение последнего уравнения, как правило, не вызывает проблем.
Задача. Решить уравнение: 7 x − 2 = 49.
Решение. 7 x − 2 = 49 ⇔ 7 x − 2 = 7 2 ⇔ x − 2 = 2 ⇔ x = 4.
Задача. Решить уравнение: 6 16 − x = 1/36.
Решение. 6 16 − x = 1/36 ⇔ 6 16 − x = 6 −2 ⇔ 16 − x = −2 ⇔ x = 18.
Немного о преобразовании показательных уравнений. Если исходное уравнение отличается от a f ( x ) = k , применяем правила работы со степенями:
- a n · a m = a n + m ,
- a n / a m = a n − m ,
- ( a n ) m = a n · m .
Кроме того, надо знать правила замены корней и дробей на степени с рациональным показателем:
Такие уравнения встречаются в ЕГЭ крайне редко, но без них разбор задачи B7 был бы неполным.
Задача. Решить уравнение: (5/7) x − 2 · (7/5) 2 x − 1 = 125/343
- (7/5) 2 x − 1 = ((5/7) −1 ) 2 x − 1 = (5/7) 1 − 2 x ,
- 125/343 = (5 3) /(7 3 ) = (5/7) 3 .
Имеем: (5/7) x − 2 · (7/5) 2 x − 1 = 125/343 ⇔ (5/7) x − 2 · (5/7) 1 − 2 x = (5/7) 3 ⇔ (5/7) x − 2 + 1 − 2 x = (5/7) 3 ⇔ (5/7) − x − 1 = (5/7) 3 ⇔ − x − 1 = 3 ⇔ x = −4.
Иррациональные уравнения
Под иррациональным понимается любое уравнение, содержащее знак корня. Из всего многообразия иррациональных уравнений мы рассмотрим лишь простейший случай, когда уравнение имеет вид:
Чтобы решить такое уравнение, возведем обе стороны в квадрат. Получим уравнение f ( x ) = a 2 . При этом автоматически выполняется требование ОДЗ: f ( x ) ≥ 0, т.к. a 2 ≥ 0. Остается решить несложное уравнение f ( x ) = a 2 .
Возводим обе стороны в квадрат и получим: 5 x − 6 = 8 2 ⇔ 5 x − 6 = 64 ⇔ 5 x = 70 ⇔ x = 14.
Сначала, как и в прошлый раз, возводим обе стороны в квадрат. А затем внесем знак «минус» в числитель. Имеем:
Заметим, что при x = −4 под корнем будет положительное число, т.е. требование ОДЗ выполнено.
Решение рациональных, иррациональных, показательных, тригонометрических и логарифмических уравнений и систем
- Опубликовано 16.09.2020Подготовка к ЕГЭ
Решение рациональных, иррациональных, показательных, тригонометрических и логарифмических уравнений и систем
На сегодняшний день ЕГЭ по математике проходит в форме решения заданий, содержащихся в контрольно-измерительных материалах, при этом, ответы на задания выносят на отдельный бланк.
Уравнения могут быть следующих видов:
В данной статье рассмотрена профильная математика, а именно раздел по видам и системам рациональных, иррациональных, показательных, тригонометрических и логарифмических уравнений.
При решении уравнений нужно помнить основные термины:
— Корнем уравнения называют неизвестное число, которое нужно найти;
— Решение уравнения предполагает нахождение его корня;
— Уравнения, у которых совпадают решения называют равносильными;
— ОДЗ – область допустимых значений;
— Если возможно заменить переменные, то нужно это выполнить;
— После решения уравнения необходимо провести проверку на правильность нахождения корня.
Итак, рассмотрим каждый вид уравнений по отдельности, включая примеры решения.
- Рациональные уравнения – уравнения, у которых, как правило, слева расположено рациональное выражение, а справа – ноль.
Рациональным уравнением называют уравнение вида r(х)=0.
Если обе части уравнения являются рациональными выражениями, то рациональные уравнения называют целыми.
Дробно-рациональным называют уравнение, которое содержит дробное выражение.
Порядок действий при решении данного вида уравнения должен быть следующий:
— Все члены должны быть переведены в левую часть уравнения;
— Данную часть уравнения нужно представить в виде дроби p(x)/q(x);
— Для полученного решения нужно провести проверку, то есть.
При решение этого рационального уравнения понадобится формула (а-в)2=а2-2ав+в2.
Рассмотрим ещё один пример решения рационального уравнения:
На основе примеров показано, что рациональные уравнения могут быть с разным количеством переменных.
Иррациональными уравнениями считают уравнения с переменной под корнем. Для того, чтобы определить является ли уравнение иррациональным нужно просто посмотреть на корень переменной. Следует учитывать, что в некоторых учебниках по математике иррациональное уравнение определяют другим способом.
Способы решения таких уравнений:
— Возвести в степень обе части уравнения;
— Ввести новые переменные;
Пример решения уравнения по первому способу:
Пример решения по второму способу:
- Показательные уравнения
Показательные уравнения – уравнение, содержащее неизвестный показатель.
В учебниках по математике разных авторов определение показательного уравнения может отличаться. Обычно такие отличия касаются незначительных деталей.
Как правило, это уравнения вида af(x)=ag(x), где а не равно одному и число а больше нуля. Из этого следует, что f(x)=g(x).
— Уравнение с одним основанием;
— Уравнение с равными основаниями.
Существует следующие способы решения таких уравнений:
— Использовать метод логарифмов;
— Привести уравнение к квадратному виду;
— Вынести за скобку общий множитель;
— Ввести новую переменную.
Итак, как решить показательное уравнение? Любое по сложности уравнение нужно привести в простую форму.
Рассмотрим наиболее простой пример решения показательного уравнения:
Для решения данного уравнения следует 2 возвести во вторую степень.
Решение даже простейших показательных уравнений имеет большую значимость. Поэтому далее вам будет легче решать уравнения более сложного уровня.
Данная тема является одной из самых сложных, поэтому следует внимательно подойти к изучению данной темы. Известны три формулы тригонометрических уравнений, запомнить которые не составляет особой сложности.
Наиболее простое тригонометрическое уравнение имеет вид sin x=a, cos x=a, tg x=а, а – число действительное.
Способы решения таких уравнений:
— Решение с помощью форму и приведение к простейшему;
— Ввод других переменных;
— Разложить уравнение по множителям.
Пример решения тригонометрического уравнения:
Здесь нужно рисовать окружность, далее выделить точки с координатой ½, соответственно, это точки 5п/6 и п/6. Если пройти по окружности, исходя из данных точек, то х=п/6+2пk, x=5п/6+2пn. При этом синус и косинус принадлежат промежутку [-1;1]. Если при решении уравнения в его правой части стоит число не принадлежащее промежутку, считается, что уравнение не имеет решения.
Также рассмотрим пример решения уравнения, разложив его по множителям.
Нужно применить формулу sin2x = 2sinxcosx.
2sinxcosx – sinx = 0.
sinx (2cosx – 1) = 0.
Таким образом, если один из множителей равен нулю, то решение уравнения также равно нулю.
Далее, sinx=0, x=пk.
- Логарифмические уравнения
Особое значение имеет подготовка ЕГЭ по математике логарифмы, это обусловлено тем, что в КИМах чаще всего встречаются именно этого вида уравнения.
Логарифмическое уравнение – это уравнение с неизвестной величиной, находящейся внутри логарифма.
Примерами логарифмических уравнений являются уравнения следующего вида:
Способы решения уравнений данного вида:
— Применять способ уравнивания к единице;
— Применять способ умножать на единицу;
— Применять доступные правила логарифмов;
— Введение другого основания;
— Возвести в степень.
Самым простым логарифмическим уравнением принято считать уравнение вида log a x = b, при этом основание a>0,a≠1.
Пример решения уравнения:
Сначала следует найти значение области, то есть ОДЗ. При этом нужно помнить, что под логарифмом выражение всегда положительное. Воспользуемся логарифмическим определением, представим х степью основания 2 логарифма, степень будет равна 3.
Решение уравнения является ОДЗ, то есть корень уравнения найден.
Таким образом, подобное задание ЕГЭ по математике легко можно решить, зная логарифмы и способы их решения.
Оставить Комментарий Отменить ответ
Для отправки комментария вам необходимо авторизоваться.
Выбери тему
Самые популярные записи
Наука. Основные особенности научного мышления. Естественные и социально гуманитарные науки (3 384)
Строение растения. Стебель, лист и цветок. (2 273)
ЕГЭ по обществознанию: мышление и деятельность; потребности и интересы (2 269)
Свобода и необходимость в человеческой деятельности. Свобода и ответственность. (2 231)
StudyWay
Помощь
© 2021 StudyWay. Все права защищены.
Ты можешь попробовать 3 наших закрытых занятия из курса «Прорыв».
Записаться можно через Instagram
Для этого напиши в Direct (в личку) кодовое слово «Пробный«
Что за курс и что тебя там будет ждать?
12 мощнейших онлайн занятий по 2 часа в формате вебинаров.
Содержание вебинара: повторение предыдущей темы, теория, перерыв и практика.
Воркбук (рабочая тетрадь)абсолютно к каждому уроку со всей необходимой теорией к этой теме и практикой.
Личный куратор — это твой помощник во всех учебных вопросах.
Они занимаются проверкой твоих домашних заданий, поддерживают и мотивируют двигаться дальше, даже когда хочется сдаться.
На собственной онлайн платформе тебя ждут
Домашние задания, которые необходимо решать после каждого занятия.
Все задания построены на базе создателей ЕГЭ — Котова / Лискова.
К каждому тестовому вопросу будет подробный разбор от главного куратора.
А задания, где необходимо оценить ответ (вторая часть) — будет проверять твой личный куратор и писать подробный комментарий про ошибки
Общий чат единомышленников, поделенный на команды.
Название даете совместно (например «Воробушки»)
Ты будешь двигаться сообща с однокурсниками, поддерживая и мотивируя друг друга.
За лучшую командную успеваемость всей команде будут выделены призы в конце каждого месяца (скидка на обучение, стикерпаки и т.д).
Личный помощник — это твой верный друг и помощник, который поможет тебе со всеми техническими вопросами, ответит на вопросы про поступление, да и просто может обсудить какие-то личные вопросы, поделиться переживаниями.
Доступ к уникальной «Академии косатиков».
Там ты сможешь найти:
Банк теории, банк планов, банк аргументов, курсы по работе со всей второй частью, термины, курсы по саморазвитию, полезные лайфхаки и всю подробную информация о ЕГЭ.
Игровая система на нашей платформе StudyWay👇
За выполнение заданий получаешь баллы (XP).
При достижении нового уровня у тебя открываются новые персонажи из Marvel, DC Comics, Игра престолов и Star Wars, а также на каждом новом уровне тебя ждут призы от нашей школы.

Основная ценность курса
1. Изучение теории и практики с учетом изменений в ЕГЭ 2022
2. Заложение фундамента и основы предмета
3. Прохождение всей теории для первой части
4. Нарешивание всех возможных типов заданий
5. Повышение результата с 0 до 60 баллов
Отличия тарифа «Стандарт от «Профи».
Дополнительные домашние задания
необходимо выполнять. Это значительно повысит твою успеваемость и улучшит показатели.
Дополнительное объяснение
твой личный куратор объяснит тебе тему повторно, если останется что-то не понятным
Групповые зачеты
у тебя будут зачеты с твоим личным куратором в мини группах по 5 человек. Там спрашиваются пройденные темы, термины и так далее.
Карта памяти
будешь восполнять все пройденные в удобной интеллект карте и в конце учебы у тебя выйдет файл с полноценной теорией по всем темам и разделам.
Персональный звонок куратору
1 раз в месяц ты можешь позвонить своему куратору и обсудить все волнующие тебя вопросы в течении 20 минут.
Секретный квест
1 раз в месяц ты будешь созваниваться с другим учеником курса и проводить совместные зачеты, тем самым познакомишься с новыми ребятами из других городов, уберешь страхи знакомства, повторишь и закрепишь пройденные темы.
Неравенства. Метод замены множителя (метод рационализации)
Полезный прием для решения сложных неравенств на ЕГЭ по математике – метод рационализации неравенства. Другое название — метод замены множителя. Это один из тех секретов, о которых ученику рассказывает репетитор. В учебниках о таком не написано.
Суть метода в том, чтобы от неравенства, содержащего в качестве множителей сложные показательные или логарифмические выражения, перейти к равносильному ему более простому рациональному неравенству.
Давайте для начала вспомним, что такое равносильные уравнения (или неравенства) В школьной программе этот важный вопрос почти не обсуждается. Поэтому запишем определение.
Равносильными называются уравнения, множества решений которых совпадают.
Заметим, что внешне уравнения могут быть и не похожи друг на друга.
Например, уравнения ( x − 3) 2 = 0 и x − 3 = 0 равносильны. Число 3 является единственным решением и того, и другого.
Уравнения и
также равносильны. Оба они не имеют решений. Другими словами, множество решений каждого из них – пусто.
Уравнения и
не являются равносильными. Решением первого уравнения является только x = 5. Решения второго – два числа: x = 5 и x = 1. Получается, что возведение обеих частей уравнения в квадрат в общем случае приводит к уравнению, неравносильному исходному.
Аналогичное определение – для неравенств.
Равносильными называются неравенства, множества решений которых совпадают.
Например, неравенства 0″ src=»https://latex.codecogs.com/png.latex?(x-1)(x-3)%3E0″ /> и 0″ src=»https://latex.codecogs.com/png.latex?%5Cfrac%3Cx-1%3E%3Cx-3%3E%3E0″ /> равносильны – ведь множества их решений совпадают. В этом легко убедиться с помощью метода интервалов.
Неравенства log_<2>5″ src=»https://latex.codecogs.com/png.latex?log_%3C2%3Ex%3Elog_%3C2%3E5″ /> и 5″ src=»https://latex.codecogs.com/gif.latex?x%3E&space;5″ /> также равносильны при 0″ src=»https://latex.codecogs.com/gif.latex?x%3E&space;0″ />. Заметим, что внешне эти неравенства не похожи – одно из них логарифмическое, другое алгебраическое.
Другими словами, при x > 0 неравенства 0″ src=»https://latex.codecogs.com/png.latex?log_%3C2%3Ex-log_%3C2%3E5%3E0″ /> и 0″ src=»https://latex.codecogs.com/png.latex?x-5%3E0″ /> имеют одинаковые решения. Если какое-либо число x > 0 является решением одного из них, то оно будет и решением второго.
А это значит, что при любом x > 0 выражение будет иметь такой же знак, как и выражение x − 5. Следовательно, если в какое-либо сложное неравенство входит в качестве множителя выражение
то при выполнении условия x > 0 его можно заменить на более простое x − 5 и получить неравенство, равносильное исходному.
Вот ключевой момент. На этом и основан метод рационализации – замены множителей, содержащих сложные логарифмические или показательные выражения, на более простые алгебраические множители.
Например, выражение вида , где f и g – функции от x, a – число, можно заменить на более простое ( f − g) ( a − 1) – конечно, при условии, что f(x) > 0 и g(x) > 0. Доказательство легко провести самостоятельно.
А сейчас – самое главное: волшебная таблица, позволяющая заменять сложные логарифмические (или показательные) множители в неравенствах на более простые. Эта таблица является ключом к задаче С3. Вот увидите, она выручит вас на ЕГЭ по математике:
| Сложный множитель | На что заменить |
| log h f − log h g | ( h − 1) ( f − g) |
| log h f − 1 | ( h − 1) ( f − h) |
| log h f | ( h − 1) ( f − 1) |
| h f − h g | ( h − 1) ( f − g) |
| h f − 1 | ( h − 1) · f |
| f h − g h | ( f − g) · h |
| f, g — функции от x. h — функция или число. | |
Конечно же, все выражения, которые содержат логарифмы, существуют при f, g, h > 0 и h ≠ 1.
Когда на ЕГЭ по математике вы применяете метод рационализации (замены множителя), — обязательно поясните, что вы им воспользовались. И не забудьте доказать соответствующую формулу. Иначе можно потерять балл.
Обратите внимание, что мы говорим о замене множителя в неравенствах вида 
Перейдем к практике – к решению задач из вариантов ЕГЭ по математике Профильного уровня.
1.
ОДЗ неравенства:
Применим метод рационализации. В соответствии с нашей таблицей, множитель заменим на (2 − x − 1)( x + 2 − 1). Множитель вида
заменим на ( x + 3 − 1)(3 − x − 1). Таким образом, от логарифмического неравенства мы перешли к рациональному:
Решим его методом интервалов:
Ответ:
2.
Заметим, что выражение положительно при x ∈ ОДЗ. Умножим обе части неравенства на это выражение.
Упростим числитель правой части неравенства:
Поделим обе части неравенства на 5 x > 0:
Неравенство уже намного проще, чем исходное. Но основания степеней разные! Чтобы применить метод рационализации, нам придется представить 2 x − 1 в виде степени с основанием 3.
Неравенство примет вид:
Воспользуемся методом замены множителя. Множитель вида h f −h g можно заменить на ( h − 1) ( f − g). Да и логарифм в знаменателе можно заменить на выражение x + 1.
Оценим
. Это необходимо сделать, чтобы правильно расставить точки на числовой прямой.

3.
Постараемся упростить это неравенство. Область допустимых значений
0;\\ x+1\neq 0. \end
Преобразуем числители выражений в левой и правой части и сделаем замену log2 x = t
Теперь обе части неравенства можно сократить на 5 t > 0.
Поскольку , выражение 2 t−1 можно записать как 3 ( t−1)·log32
Заметим, что log32 − 2 t. Решим его:

Вернемся к переменной x:
или
Ответ:
4. Еще одна задача из той же серии.
Запишем ОДЗ:
Умножим обе части неравенства на 0″ src=»https://latex.codecogs.com/png.latex?log%5E%3C2%3E_%3C2%3E32x%3E0″ />. Постараемся упростить числители выражений в левой и правой части.
Поделим обе части неравенства на 0.» src=»https://latex.codecogs.com/png.latex?2%5E%3Clog_%3C2%3E(4x)%3E%3E0.» />
Хорошо бы сделать замену. Пусть log2(4 x) = t. Тогда:
Неравенство примет вид:
Мы уже знаем, как представить число 7 в виде степени числа 2:
Применим метод рационализации.
Оценим
Применим в левой части неравенства формулу перехода к другому основанию
Последовательно применим метод замены множителя, то есть метод рационализации.
Напомним, что множитель log h f можно заменить на ( h-1)( f-1), а множитель (log h f — 1) — на ( h — 1)( f — h).
Поскольку 0″ src=»https://latex.codecogs.com/png.latex?(x+5)%5E%3C2%3E%3E0″ /> при x ∈ ОДЗ, а 0″ src=»https://latex.codecogs.com/png.latex?2x%5E%3C2%3E+10x+14%3E0″ /> > 0 при всех x, получим:

Посмотрим, чем поможет метод замены множителя в решении сложного показательного неравенства.
6. Решите неравенство:
Числитель дроби в левой части — однородное выражение, где каждое слагаемое имеет степень 2х. Поделим обе части неравенства на
Поскольку , поделим обе части неравенства на
Применяя метод рационализации, множитель вида заменяем на
Остается решить неравенство методом интервалов. Но как сравнить и ?
Что больше? Давайте представим как логарифм с основанием
7. Теперь логарифмическое неравенство. Обратите внимание, что здесь лучше всего записывать решение в виде цепочки равносильных переходов. И само неравенство, которое мы упрощаем, и область его допустимых значений мы записываем в одну систему. И решаем ее.
Мы объединили в систему и область допустимых значений, и само неравенство. Применим формулу логарифма частного, учитывая, что
Используем также условия
Обратите внимание, как мы применили формулу для логарифма степени. Строго говоря,
Согласно методу замены множителя, выражение заменим
Решить ее легко.
8. А теперь неравенство с ловушкой. Мы надеемся, что вы помните — нельзя извлекать корень из неравенства.
Извлекать корень из неравенства нельзя! Можно перенести все в левую часть неравенства и разложить на множители как разность квадратов:
Применим формулы разности и суммы логарифмов, следя за областью допустимых значений. Все выражения под логарифмами в исходном неравенстве должны быть положительны.
Посмотрим на второе и третье неравенства системы. Поскольку х+5 положительно, то и выражение должно быть положительно.
Заметим, что решения неравенства — это все числа, кроме
По методу рационализации, каждый из множителей вида заменяем на
Просто равносильные преобразования. Выражение положительно всегда — так как в уравнении дискриминант отрицателен. Осталось применить метод интервалов.
http://thestudyway.com/education_ege/logarifmicheskie_trigonometricheskie_sistemy/
http://ege-study.ru/ru/ege/materialy/matematika/pokazatelnye-i-logarifmicheskie-neravenstva-chast-2/