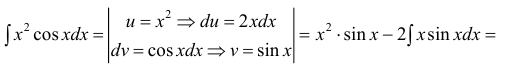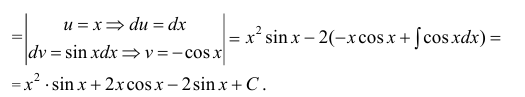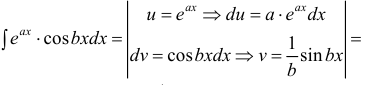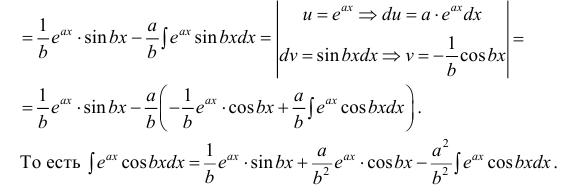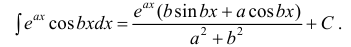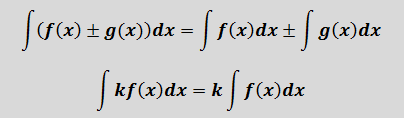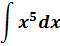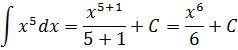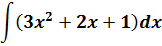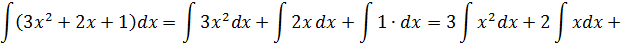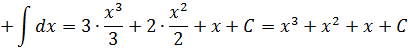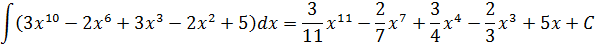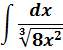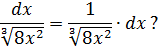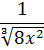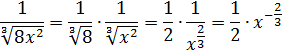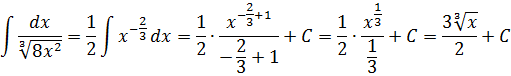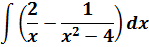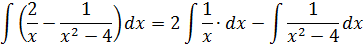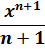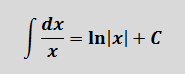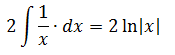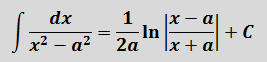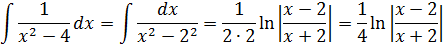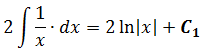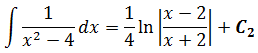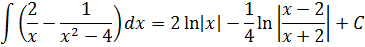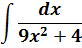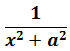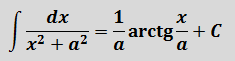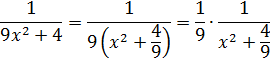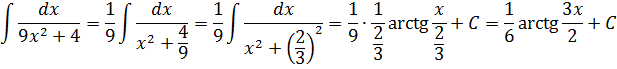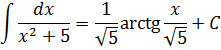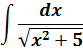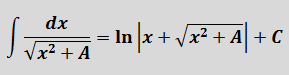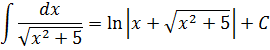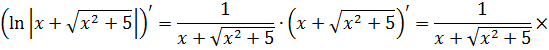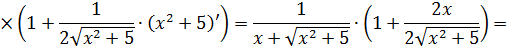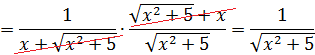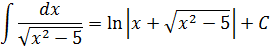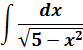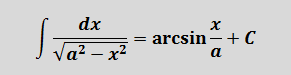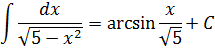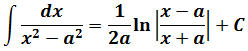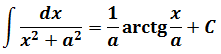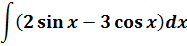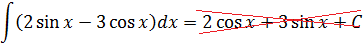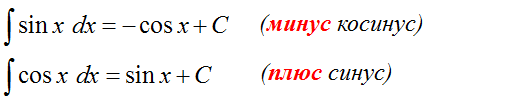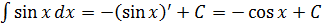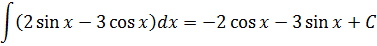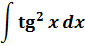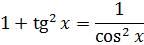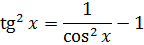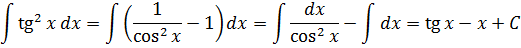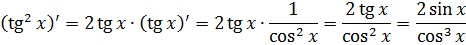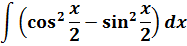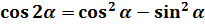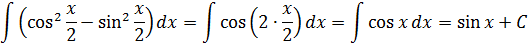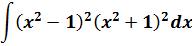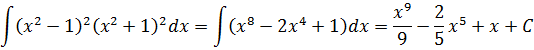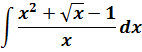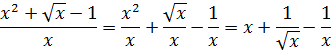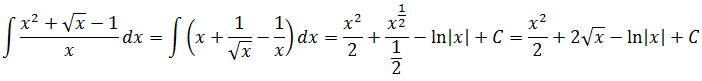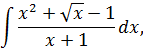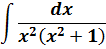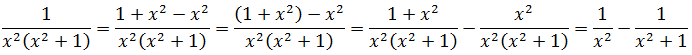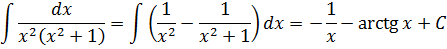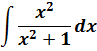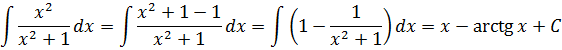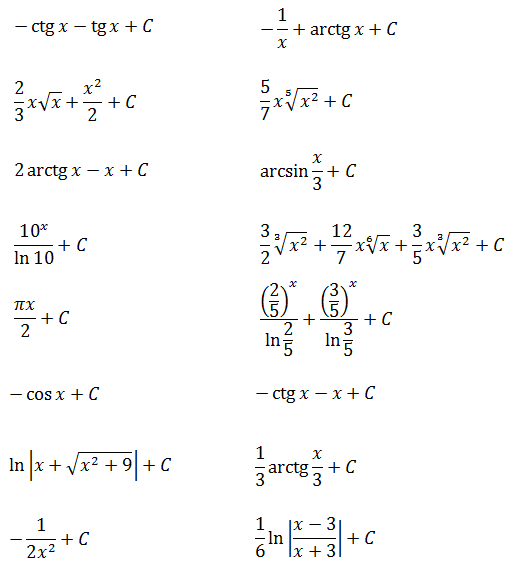Методы интегрирования неопределенного интеграла с примерами решения
Содержание:
При решении многих практических задач таких, как вычисление длин линий, площадей, отыскание траекторий движения и других, вводится понятие интегрирования.
Определения
Определение: Первообразной функции
Теорема: (о существовании первообразной) Если функция f(x) непрерывна на сегменте 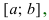
Теорема: Если F(x) — первообразная функции f(х), то функция F(x) + C (С -произвольная постоянная) также является первообразной функции f(х).
Доказательство:
ТЗ. Если 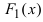
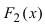
Доказательство: Пусть 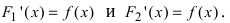
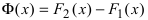
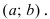
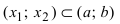
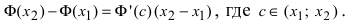
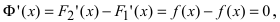
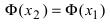
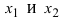
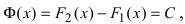
Пример:
Пусть дана функция 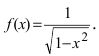
Решение:
В случае наличия двух первообразных показать, что они отличаются на постоянную величину.
Для функции существуют две первообразные 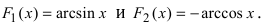
Определение: Совокупность всех первообразных функции 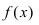
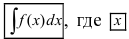
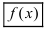
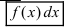
На основании теорем можно записать, что
Определение: Отыскание всех первообразных называется неопределенным интегрированием.
Выясним геометрический смысл неопределенного интеграла. Пусть дана функция 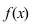
Пример:
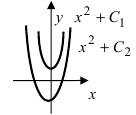
Построить кривые, которые задаются неопределенным интегралом
Решение:
Первообразной для под интегральной функции f(х) = 2х будет функция 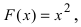
Рис. 1. Интегральные кривые
Свойства неопределенного интеграла
1. Производная от неопределенного интеграла равна под интегральной функции
Доказательство: По определению неопределенного интеграла
2. Дифференциал неопределенного интеграла равен под интегральному выра- жению
Доказательство: По определению дифференциала от неопределенного интеграла имеем
3. Если под интегральное выражение является дифференциалом некоторой функции F(x), тo неопределенный интеграл равен
Доказательство: Так как
4. Неопределенный интеграл от линейной комбинации функций равен той же самой линейной комбинации неопределенных интегралов от этих функций
- а) неопределенный интеграл от суммы (разности) функций равен сумме (разности) неопределенных интегралов от этих функций
- б) постоянный множитель можно выносить за знак неопределенного интеграла
5. Формула неопределенного интеграла не зависит от обозначения переменной интегрирования
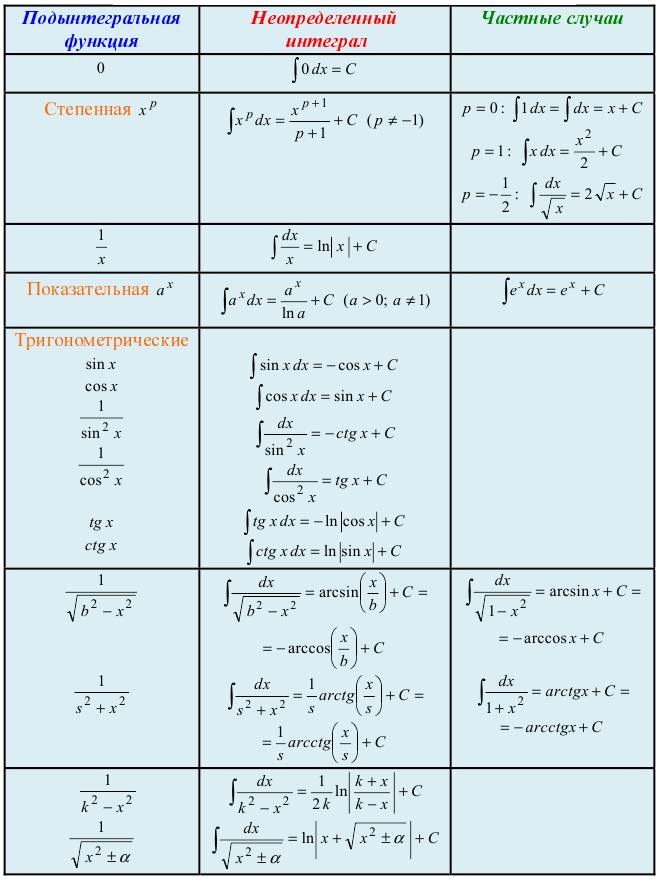
Таблица основных неопределенных интегралов
Методы интегрирования
Метод тождественных преобразований под интегральной функции
Данный метод основан на использовании простых приемов, алгебраических и тригонометрических формул, свойств подынтегральной функции, разложения полиномов на простые множители и свойств неопределенного интеграла. Рассмотрим этот метод на конкретных примерах.
1. Почленное деление числителя дроби на ее знаменатель
Замечание: Следует запомнить, что нет формулы почленного деления знаменателя дроби на ее числитель, т.е.
Пример:
Найти
Решение:
Выполним в под интегральной функции почленное деление числителя дроби на ее знаменатель и воспользуемся свойством линейности неопределенного интеграла
Замечание: Из этого примера видно, что слова «найти неопределенный интеграл” означают: за счет преобразований подынтегральной функции и использования свойств неопределенного интеграла данный интеграл надо привести к совокупности табличных интегралов и воспользоваться этой таблицей.
Замечание: Из примера также видно, что, несмотря на наличие двух табличных интегралов, константа интегрирования С пишется один раз, так как сумма или разность постоянных интегрирования все равно есть постоянная величина.
2. Использование противоположных арифметических операций (например, сложение-вычитание).
Пример:
Найти
Решение:
Анализ под интегральной функции показывает, что в числитель дроби надо добавить и вычесть 1 (при этом подынтегральная функция не изменится), а затем воспользоваться первым приемом (почленное деление числителя дроби на ее знаменатель)
3. Использование алгебраических и тригонометрических формул, например,
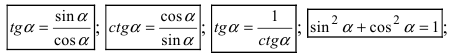
Пример:
Найти
Решение:
Воспользуемся формулой квадрата разности
Пример:
Найти
Решение:
4. Использование свойств функций, например,
Пример:
Вычислить
Решение:
Пример:
Вычислить
Решение:
5. Использование разложения полиномов на простые множители, например, 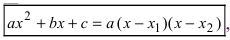
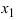
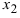
Пример:
Найти
Решение:
По теореме Виета уравнение 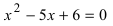
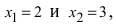
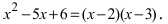
Метод замены переменной интегрирования
Данный метод основан на формуле
Метод замены переменной интегрирования применяется в двух случаях:
а) Если аргумент функции отличается от простого аргумента х, то этот сложный аргумент принимается в качестве новой переменной интегрирования t.
Пример:
Вычислить
Решение:
Так как показатель степени экспоненты отличается от простого аргумента х, то этот показатель степени принимаем в качестве новой переменной интегрирования, т.е.
Замечание: После нахождения первообразной с новой переменной интегрирования надо обязательно вернуться к старой переменной интегрирования.
Пример:
Вычислить
Решение:
Выражение, стоящее в круглых скобках, является аргументом степенной функции и отличается от простого аргумента х, поэтому принимаем его в качестве новой переменной интегрирования, т.е.
Пример:
Вычислить
Решение:
Выражение, стоящее в круглых скобках, является аргументом функции синус и отличается от простого аргумента х, поэтому принимаем его в качестве новой переменной интегрирования, т.е. 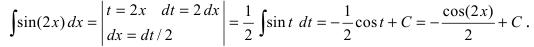
Пример:
Найти
Решение:
В подынтегральном выражении содержится элементарная функция tgx и в качестве множителя при dx присутствует ее первая производная 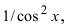
Пример:
Найти
Решение:
Данный пример объединяет первый метод с методом замены переменной интегрирования. Выполним почленное деление числителя дроби на ее знаменатель и разобьем интеграл на два интеграла, для которых применяются два случая замены переменной интегрирования
Замечание: Умение отыскивать подходящую замену вырабатывается в процессе многократных упражнений, однако можно указать ряд случаев, когда можно сразу увидеть необходимую замену переменной интегрирования при анализе подынтегрального выражения, например, 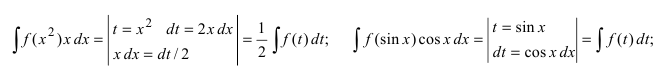
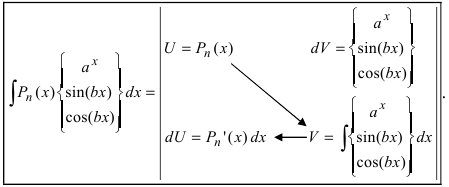
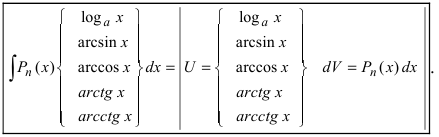
Метод интегрирования по частям
Интегрирование по частям основано на использовании формулы дифференциала от произведения двух функций 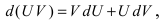
Таким образом, для неопределенного интеграла формула интегрирования по частям имеет вид:
Для того чтобы знать, какую из функций принимать за U (все остальное в подынтегральном выражении принимается за dV), рассмотрим наиболее часто встречающиеся случаи:
1. 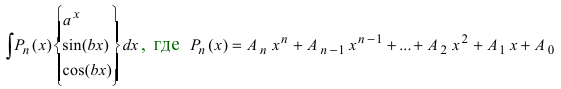
В этом случае
Замечание: Для нахождения функции dU используют определение дифференциала функции. При вычислении функции V интегрируют выражение dV, при этом постоянная интегрирования полагается равной нулю (С = 0). После выполнения этих действий применяют формулу интегрирования по частям.
Пример:
Вычислить
Решение:
Применим метод интегрирования по частям
Замечание: Из приведенного примера видно, что при необходимости метод интегрирования по частям применяется повторно.
2. Для интегралов вида
Пример:
Вычислить
Решение:
Действуя согласно методике, получим
3. Для интегралов вида 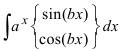
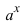
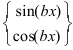
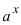
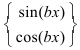
Пример:
Найти
Решение:
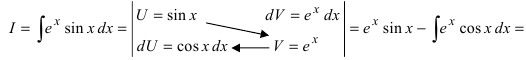
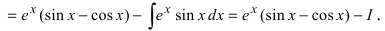
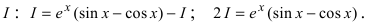
4. Нестандартные интегралы требуют для своего вычисления приобретения опыта на практических занятиях.
Пример:
Найти
Решение:
Неопределенный интеграл
Определение 1. Пусть Δ − промежуток действительной оси. Функция y=F(x) называется первообразной для функции y=f(x) на промежутке Δ, если F(x) − дифференцируема на Δ и 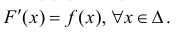
Пример:
а) F(x)=x − первообразная для 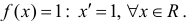
б) 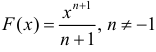
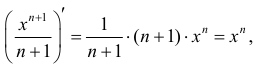
в) 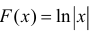
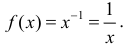
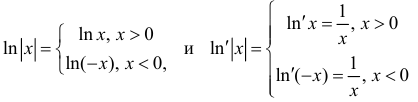
Замечание. Первообразная функция определена не однозначно. А именно,
F(x) = x+C , где С – любая константа также будет первообразной для 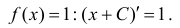
В общем случае верна теорема:
Теорема 1. Две дифференцируемые на промежутке Δ функции 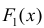
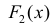
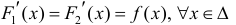
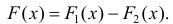
Тогда 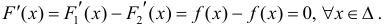
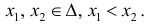
По теореме Лагранжа (теорема 4 § 12): 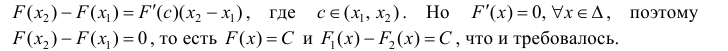
Достаточность. 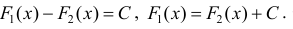
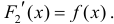
Тогда 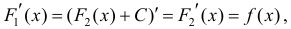
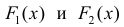
для одной и той же функции y=f(x), что и требовалось доказать.
Определение 2. Множество всех первообразных для функции y=f(x) на промежутке Δ называется неопределенным интегралом от функции f(x) и обозначается 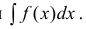
Если F(x) — одна из первообразных, то , согласно теореме 1, 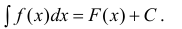
Свойства неопределенного интеграла
- Если ( ) F x — дифференцируема на Δ , то
(3) или
(4) здесь под записью
подразумеваем одну из первообразных.
- Если f (x) имеет первообразную на Δ, то λf(x) также имеет первообразную на Δ и ,если λ ≠ 0, то
(5)
- Если
имеют первообразную на Δ , тогда
также имеет первообразную на Δ и:
(6)
Свойства 1 – 4 легко выводятся из определения первообразной и интеграла
и соответствующих свойств производной.
Докажем, например, свойство 3.
Пусть F (x) — первообразная для f (x) на промежутке Δ. Тогда 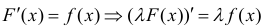
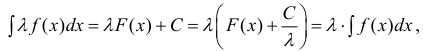
Из определений 1,2 следует, что интегрирование – действие обратное
дифференцированию (находится функция, производная которой равна данной).
Таблица интегралов
При вычислении интегралов в простых случаях применяют свойства 1 – 4.
Пример:
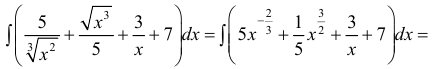
Пример:
Теорема 1. Если y=f(x) — непрерывна на промежутке Δ , то для нее ∃ первообразная функция y = F(x) на этом промежутке.
Замена переменной в неопределенном интеграле
Теорема 1. Пусть функция y = F(t) — первообразная для функции y = f(t) на промежутке 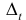
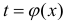
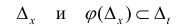
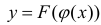
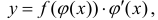
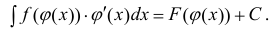
Доказательство. 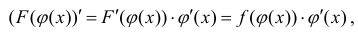
Замечание. Формулу (1) можно переписать в виде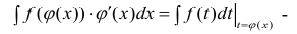
формула интегрирования с помощью подстановки 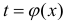
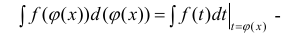
Формула интегрирования с помощью поднесения под дифференциал, когда
подынтегральную функцию 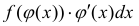
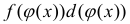
занося 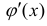
Пример:
Пример:
Пример:
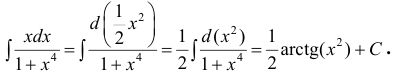
При поднесении под дифференциал можно использовать свойства
дифференциала (см. § 6) 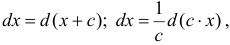
Пример:
Пример:
Пример:
Иногда в формуле (2) легче вычислять левую часть, чем правую:
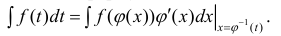
Формула (5) – формула интегрирования с помощью замены переменной 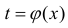
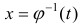
Пример:
Интегрирование по частям в неопределенном интеграле
Теорема 1. Пусть функция u(x) и v(x) – дифференцируемы на промежутке Δ и на этом промежутке 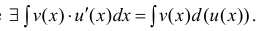
∃ и 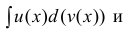
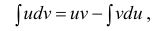
Доказательство. 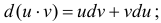
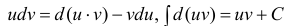
Пример:
Пример:
Замечание.
- При интегрировании выражений вида:
— многочлен степени n полагают:
После интегрирования по частям степень многочлена уменьшается на 1 (см. пример 1).
- При интегрирования выражений вида:
полагают:
(
— многочлен). После интегрирования по частям интеграл упрощается.
Пример:
Пример:
Таким образом, проинтегрировав дважды по частям, получили уравнение,
содержащее 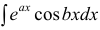
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Определённый интеграл
- Кратный интеграл
- Ряды в математике
- Дифференциальные уравнения с примерами
- Дифференциальное исчисление функций одной переменной
- Исследование функции
- Пространство R»
- Неопределённый интеграл
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Вычисление простейших неопределённых интегралов
И снова здравствуйте, друзья!
Как я и обещал, с этого урока мы начнём бороздить бескрайние просторы поэтического мира интегралов и приступим к решению самых разнообразных (порой, очень красивых) примеров. 🙂
Чтобы грамотно ориентироваться во всём интегральном многообразии и не заблудиться, нам потребуется всего четыре вещи:
1) Таблица интегралов. Все подробности о ней — в предыдущем материале. Как именно с ней работать — в этом.
2) Свойства линейности неопределённого интеграла (интеграл суммы/разности и произведения на константу).
3) Таблица производных и правила дифференцирования.
Да-да, не удивляйтесь! Без умения считать производные, в интегрировании ловить совершенно нечего. Согласитесь, бессмысленно, например, учиться делению, не умея умножать. 🙂 И очень скоро вы увидите, что без отточенных навыков дифференцирования не посчитать ни один сколь-нибудь серьёзный интеграл, выходящий за рамки элементарных табличных.
4) Методы интегрирования.
Их очень и очень много. Для конкретного класса функций — свой. Но среди всего их богатого разнообразия выделяется три базовых:
О каждом из них — в отдельных уроках.
А теперь, наконец, приступим к решению долгожданных примеров. Чтобы не скакать из раздела в раздел, я продублирую ещё разок весь джентльменский набор, который пригодится для нашей дальнейшей работы. Пусть весь инструментарий будет под рукой.)
Прежде всего, это таблица интегралов:
Кроме того, нам понадобятся базовые свойства неопределённого интеграла (свойства линейности):
Что ж, необходимая снаряга подготовлена. Пора в путь! 🙂
Прямое применение таблицы
В данном параграфе будут рассматриваться самые простые и безобидные примеры. Алгоритм здесь прост до ужаса:
1) Смотрим в таблицу и ищем нужную формулу (формулы);
2) Применяем свойства линейности (где требуется);
3) Осуществляем превращение по табличным формулам и прибавляем в конце константу С (не забываем!) ;
4) Записываем ответ.
Пример 1
Такой функции в нашей таблице нет. Зато есть интеграл от степенной функции в общем виде (вторая группа). В нашем случае n = 5. Вот и подставляем пятёрку вместо n и аккуратно считаем результат:
Разумеется, этот пример совсем примитивный. Чисто для знакомства.) Зато умение интегрировать степени позволяет легко считать интегралы от любых многочленов и прочих степенных конструкций.
Пример 2
Под интегралом сумма. Ну и ладно. У нас на этот случай есть свойства линейности. 🙂 Разбиваем наш интеграл на три отдельных, выносим все константы за знаки интегралов и считаем каждый по таблице (группа 1-2):
Прошу обратить внимание: константа С появляется именно в тот момент, когда исчезают ВСЕ знаки интеграла! Конечно, после этого приходится её постоянно таскать за собой. А что делать…
Разумеется, так подробно расписывать обычно не требуется. Это чисто для понимания сделано. Чтобы суть уловить.)
Например, очень скоро, особо не раздумывая, вы в уме будете давать ответ к монстрам типа:
Многочлены — самые халявные функции в интегралах.) А уж в диффурах, в физике, в сопромате и прочих серьёзных дисциплинах интегрировать многочлены придётся постоянно. Привыкайте.)
Следующий примерчик будет чуть покруче.
Пример 3
Надеюсь, всем понятно, что наше подынтегральное выражение можно расписать вот так:
Подынтегральная функция отдельно, а множитель dx (значок дифференциала) — отдельно.
Замечание: в этом уроке множитель dx в процессе интегрирования пока никак не участвует, и мы на него пока что мысленно «забиваем». 🙂 Работаем только с подынтегральной функцией. Но забывать про него не будем. Совсем скоро, буквально на следующем уроке, посвящённом подведению функции под знак дифференциала , мы про него вспомним. И ощутим всю важность и мощь этого значка в полную силу!)
А пока наш взор обращён на подынтегральную функцию
Не очень похоже на степенную функцию, но это она. 🙂 Если вспомнить школьные свойства корней и степеней, то вполне можно преобразовать нашу функцию:
А икс в степени минус две трети — это уже табличная функция! Вторая группа, n=-2/3. А константа 1/2 нам не помеха. Выносим её наружу, за знак интеграла, и прямо по формуле считаем:
В этом примере нам помогли элементарные свойства степеней. И так надо делать в большинстве случаев, когда под интегралом стоят одинокие корни или дроби. Посему пара практических советов при интегрировании степенных конструкций:
Заменяем дроби степенями с отрицательными показателями;
Заменяем корни степенями с дробными показателями.
А вот в окончательном ответе переход от степеней обратно к дробям и корням — дело вкуса. Лично я перехожу обратно — так эстетичнее, что ли.
И, пожалуйста, аккуратно считаем все дроби! Внимательно следим за знаками и за тем, что куда идёт — что в числитель, а что знаменатель.
Что? Надоели уже скучные степенные функции? Ну ладно! Берём быка за рога!
Пример 4
Если сейчас привести всё под интегралом к общему знаменателю, то можно застрять на этом примере всерьёз и надолго.) Но, присмотревшись повнимательнее к подынтегральной функции, можно заметить, что наша разность состоит из двух табличных функций. Так что не будем извращаться, а вместо этого разложим наш интеграл на два:
Первый интеграл — обычная степенная функция, (2-я группа, n = -1): 1/x = x -1 .
Традиционная наша формула для первообразной степенной функции
здесь не работает, но зато у нас для n = -1 есть достойная альтернатива — формула с натуральным логарифмом. Вот эта:
Тогда, согласно этой формуле, первая дробь проинтегрируется так:
А вторая дробь — тоже табличная функция! Узнали? Да! Это седьмая формула с «высоким» логарифмом:
Константа «а» в этой формуле равна двойке: a=2.
Важное замечание: Обратите внимание, константу С при промежуточном интегрировании я нигде не приписываю! Почему? Потому что она пойдёт в окончательный ответ всего примера. Этого вполне достаточно.) Строго говоря, константу надо писать после каждого отдельного интегрирования — хоть промежуточного, хоть окончательного: так уж неопределённый интеграл требует…)
Например, после первого интегрирования я должен был бы написать:
После второго интегрирования:
Но вся фишка в том, что сумма/разность произвольных констант — это тоже некоторая константа! В нашем случае для окончательного ответа нам надо из первого интеграла вычесть второй. Тогда у нас получится разность двух промежуточных констант:
И мы имеем полное право эту самую разность констант заменить одной константой! И просто переобозначить её привычной нам буквой «С». Вот так:
Вот и приписываем эту самую константу С к окончательному результату и получаем ответ:
Да-да, дроби они такие! Многоэтажные логарифмы при их интегрировании — самое обычное дело. Тоже привыкаем.)
Запоминаем:
При промежуточном интегрировании нескольких слагаемых константу С после каждого из них можно не писать. Достаточно включить её в окончательный ответ всего примера. В самом конце.
Следующий пример тоже с дробью. Для разминки.)
Пример 5
В таблице, понятное дело, такой функции нет. Но зато есть похожая функция:
Это самая последняя, восьмая формула. С арктангенсом. 🙂
И нам сам бог велел подстроить наш интеграл под эту формулу! Но есть одна проблемка: в табличной формуле перед х 2 никакого коэффициента нету, а у нас — девятка. Не можем пока что напрямую воспользоваться формулой. Но в нашем случае проблема вполне решаема. Вынесем эту девятку сначала за скобки, а потом вообще уведём за пределы нашей дроби.)
А новая дробь — уже нужная нам табличная функция под номером 8! Здесь а 2 =4/9. Или а=2/3.
Всё. Выносим 1/9 за знак интеграла и пользуемся восьмой формулой:
Вот такой ответ. Этот пример, с коэффициентом перед х 2 , я специально так подобрал. Чтобы ясно было, что делать в таких случаях. 🙂 Если перед х 2 никакого коэффициента нет, то такие дроби тоже будут в уме интегрироваться.
Здесь а 2 = 5, поэтому само «а» будет «корень из пяти». В общем, вы поняли.)
А теперь немного видоизменим нашу функцию: напишем знаменатель под корнем.) Вот такой интеграл теперь будем брать:
Пример 6
В знаменателе появился корень. Естественно, изменилась и соответствующая формула для интегрирования, да.) Опять лезем в таблицу и ищем подходящую. Корни у нас есть в формулах 5-й и 6-й групп. Но в шестой группе под корнями только разность. А у нас — сумма. Значит, работаем по пятой формуле, с «длинным» логарифмом:
Число А у нас — пятёрка. Подставляем в формулу и получаем:
И все дела. Это ответ. Да-да, так просто!)
Если закрадываются сомнения, то всегда можно (и нужно) проверить результат обратным дифференцированием. Проверим? А то вдруг, лажа какая-нибудь?
Дифференцируем (на модуль внимания не обращаем и воспринимаем его как обычные скобки):
Кстати, если в подынтегральной функции под корнем поменять знак с плюса на минус, то формула для интегрирования останется той же самой. Не случайно в таблице под корнем стоит плюс/минус. 🙂
Важно! В случае минуса, на первом месте под корнем должно стоять именно х 2 , а на втором — число. Если же под корнем всё наоборот, то и соответствующая табличная формула будет уже другая!
Пример 7
Под корнем снова минус, но х 2 с пятёркой поменялись местами. Похоже, но не одно и то же… На этот случай в нашей таблице тоже есть формулка.) Формула номер шесть, с ней мы ещё не работали:
А вот теперь — аккуратно. В предыдущем примере у нас пятёрка выступала в роли числа A. Здесь же пятёрка будет выступать уже в роли числа а 2 !
Поэтому для правильного применения формулы не забываем извлечь корень из пятёрки:
И теперь пример решается в одно действие. 🙂
Вот так вот! Всего лишь поменялись местами слагаемые под корнем, а результат интегрирования изменился существенно! Логарифм и арксинус… Так что, пожалуйста, не путайте эти две формулы! Хотя подынтегральные функции и очень похожи…
В табличных формулах 7-8 перед логарифмом и арктангенсом присутствуют коэффициенты 1/(2а) и 1/а соответственно. И в тревожной боевой обстановке при записи этих формул даже закалённые учёбой ботаны частенько путаются, где просто 1/а, а где 1/(2а). Вот вам простой приёмчик для запоминания.
в знаменателе подынтегральной функции стоит разность квадратов х 2 — а 2 . Которая, согласно боянной школьной формуле, раскладывается как (х-а)(х+а). На два множителя. Ключевое слово — два. И эти две скобки при интегрировании идут в логарифм: с минусом вверх, с плюсом — вниз.) И коэффициент перед логарифмом тоже 1/(2а).
А вот в формуле №8
в знаменателе дроби стоит сумма квадратов. Но сумма квадратов x 2 +a 2 неразложима на более простые множители. Поэтому, как ни крути, в знаменателе так и останется один множитель. И коэффициент перед арктангенсом тоже будет 1/а.
А теперь для разнообразия проинтегрируем что-нибудь из тригонометрии.)
Пример 8
Пример простой. Настолько простой, что народ, даже не глядя в таблицу, тут же радостно ответ пишет и… приехали. 🙂
Следим за знаками! Это самая распространённая ошибка при интегрировании синусов/косинусов. Не путаем с производными!
Но!
Поскольку производные народ обычно худо-бедно помнит, то, чтобы не путаться в знаках, приём для запоминания интегралов тут очень простой:
Интеграл от синуса/косинуса = минус производная от тех же синуса/косинуса.
Например, мы ещё со школы знаем, что производная синуса равна косинусу:
Тогда для интеграла от того же синуса будет справедливо:
И всё.) С косинусом то же самое.
Исправляем теперь наш пример:
Предварительные элементарные преобразования подынтегральной функции
До этого момента были самые простенькие примеры. Чтобы прочувствовать, как работает таблица и не ошибаться в выборе формулы.)
Конечно, мы делали кое-какие простенькие преобразования — множители выносили, на слагаемые разбивали. Но ответ всё равно так или иначе лежал на поверхности.) Однако… Если бы вычисление интегралов ограничивалось только прямым применением таблицы, то вокруг была бы сплошная халява и жить стало бы скучно.)
А теперь разберём примеры посолиднее. Такие, где впрямую, вроде бы, ничего и не решается. Но стоит вспомнить буквально пару-тройку элементарных школьных формул или преобразований, как дорога к ответу становится простой и понятной. 🙂
Продолжим развлекаться с тригонометрией.
Пример 9
Такой функции в таблице и близко нет. Зато в школьной тригонометрии есть такое малоизвестное тождество:
Выражаем теперь из него нужный нам квадрат тангенса и вставляем под интеграл:
Зачем это сделано? А затем, что после такого преобразования наш интеграл сведётся к двум табличным и будет браться в уме!
А теперь проанализируем наши действия. На первый взгляд, вроде бы, всё проще простого. Но давайте задумаемся вот над чем. Если бы перед нами стояла задача продифференцировать ту же самую функцию, то мы бы точно знали, что именно надо делать — применять формулу производной сложной функции:
И всё. Простая и безотказная технология. Работает всегда и гарантированно приводит к успеху.
А что же с интегралом? А вот тут нам пришлось порыться в тригонометрии, откопать какую-то малопонятную формулу в надежде, что она нам как-то поможет выкрутиться и свести интеграл к табличному. И не факт, что помогла бы она нам, совсем не факт… Именно поэтому интегрирование — более творческий процесс, нежели дифференцирование. Искусство, я бы даже сказал. 🙂 И это ещё не самый сложный пример. То ли ещё будет!
Пример 10
Что, внушает? Таблица интегралов пока бессильна, да. Но, если снова заглянуть в нашу сокровищницу тригонометрических формул, то можно откопать весьма и весьма полезную формулу косинуса двойного угла:
Вот и применяем эту формулу к нашей подынтегральной функции. В роли «альфа» у нас х/2.
Эффект потрясающий, правда?
Эти два примера наглядно показывают, что предварительное преобразование функции перед интегрированием вполне допускается и порой колоссально облегчает жизнь! И в интегрировании эта процедура (преобразование подынтегральной функции) на порядок более оправдана, чем при дифференцировании. В дальнейшем всё увидите.)
Разберём ещё парочку типовых преобразований.
Формулы сокращённого умножения, раскрытие скобок, приведение подобных и метод почленного деления.
Обычные банальные школьные преобразования. Но порой только они и спасают, да.)
Пример 11
Если бы мы считали производную, то никаких проблем: формула производной произведения и — вперёд. Но стандартной формулы для интеграла от произведения не существует. И единственный выход здесь — раскрыть все скобки, чтобы под интегралом получился многочлен. А уж многочлен мы как-нибудь проинтегрируем.) Но скобки раскрывать тоже будем с умом: формулы сокращённого умножения — штука мощная!
(x 2 — 1) 2 (x 2 + 1) 2 = ((x 2 — 1)(x 2 + 1)) 2 = ((x 2 ) 2 — 1 2 ) 2 = (x 4 — 1) 2 = x 8 — 2x 4 + 1
А теперь считаем:
Пример 12
Опять же, стандартной формулы для интеграла от дроби не существует. Однако в знаменателе подынтегральной дроби стоит одинокий икс. Это в корне меняет ситуацию.) Поделим почленно числитель на знаменатель, сведя нашу жуткую дробь к безобидной сумме табличных степенных функций:
Особо комментировать процедуру интегрирования степеней не буду: не маленькие уже.)
Интегрируем сумму степенных функций. По табличке.)
Вот и все дела.) Кстати, если бы в знаменателе сидел не икс, а, скажем, х+1, вот так:
то этот фокус с почленным делением уже так просто не прошёл бы. Именно из-за наличия корня в числителе и единицы в знаменателе. Пришлось бы замену вводить и избавляться от корня. Но такие интегралы гораздо сложнее. О них — в других уроках.
Видите! Стоит только чуть-чуть видоизменить функцию — тут же меняется и подход к её интегрированию. Порой кардинально!) Нету чёткой стандартной схемы. К каждой функции — свой подход. Иногда даже уникальный.)
В некоторых случаях преобразования в дробях ещё более хитрые.
Пример 13
А здесь как можно свести интеграл к набору табличных? Здесь можно ловко извернуться добавлением и вычитанием выражения x 2 в числителе дроби с последующим почленным делением. Очень искусный приём в интегралах! Смотрите мастер-класс! 🙂
И теперь, если заменить исходную дробь на разность двух дробей, то наш интеграл распадается на два табличных — уже знакомую нам степенную функцию и арктангенс (формула 8):
Ну, что тут можно сказать? Вау!
Этот трюк с добавлением/вычитанием слагаемых в числителе — очень популярен в интегрировании рациональных дробей. Очень! Рекомендую взять на заметку.
Пример 14
Здесь тоже рулит эта же технология. Только добавлять/вычитать надо единичку, чтобы из числителя выделить выражение, стоящее в знаменателе:
Вообще говоря, рациональные дроби (с многочленами в числителе и знаменателе) — отдельная очень обширная тема. Дело всё в том, что рациональные дроби — один из очень немногих классов функций, для которых универсальный способ интегрирования существует. Метод разложения на простейшие дроби вкупе с методом неопределённых коэффициентов. Но способ этот очень трудоёмкий и обычно применяется как тяжёлая артиллерия. Ему будет посвящён не один урок. А пока что тренируемся и набиваем руку на простых функциях.
Подытожим сегодняшний урок.
Сегодня мы подробно рассмотрели, как именно пользоваться таблицей, со всеми нюансами, разобрали множество примеров (и не самых тривиальных) и познакомились с простейшими приёмами сведения интегралов к табличным. И так мы теперь будем поступать всегда. Какая бы страшная функция ни стояла под интегралом, с помощью самых разнообразных преобразований мы будем добиваться того, чтобы, рано или поздно, наш интеграл, так или иначе, свёлся к набору табличных.
Несколько практических советов.
1) Если под интегралом дробь, в числителе которой сумма степеней (корней), а в знаменателе — одинокая степень икса, то используем почленное деление числителя на знаменатель. Заменяем корни степенями с дробными показателями и работаем по формулам 1-2.
2) В тригонометрических конструкциях в первую очередь пробуем базовые формулы тригонометрии — двойного/тройного угла, основные тригонометрические тождества:
Может очень крупно повезти. А может и нет…
3) Где нужно (особенно в многочленах и дробях), применяем формулы сокращённого умножения:
(a+b) 2 = a 2 +2ab+b 2
4) При интегрировании дробей с многочленами пробуем искусственно выделить в числителе выражение(я), стоящее(щие) в знаменателе. Очень часто дробь упрощается и интеграл сводится к комбинации табличных.
Ну что, друзья? Я вижу, интегралы вам начинают нравиться. 🙂 Тогда набиваем руку и решаем примеры самостоятельно.) Сегодняшнего материала вполне достаточно, чтобы успешно с ними справиться.
Что? Не знаете, как интегрировать арксинус/арккосинус ? Да! Мы этого ещё не проходили.) Но здесь их напрямую интегрировать и не нужно. И да поможет вам школьный курс!)
Ответы (в беспорядке):
Для лучших результатов настоятельно рекомендую приобрести сборник задач по матану Г.Н. Бермана. Классная штука!
Понятие и свойства неопределённого интеграла, таблица интегралов
Неопределённый интеграл: 8 фактов, которые надо знать студенту
Первообразная функция и неопределённый интеграл
Факт 1. Интегрирование — действие, обратное дифференцированию, а именно, восстановление функции по известной производной этой функции. Восстановленная таким образом функция F(x) называется первообразной для функции f(x).
Определение 1. Функция F(x) называется первообразной для функции f(x) на некотором промежутке X, если для всех значений x из этого промежутка выполняется равенство F ‘(x)=f(x), то есть данная функция f(x) является производной от первообразной функции F(x)..
Например, функция F(x) = sin x является первообразной для функции f(x) = cos x на всей числовой прямой, так как при любом значении икса (sin x)’ = (cos x) .
Определение 2. Неопределённым интегралом функции f(x) называется совокупность всех её первообразных. При этом употребляется запись
где знак ∫ называется знаком интеграла, функция f(x) – подынтегральной функцией, а f(x)dx – подынтегральным выражением.
Таким образом, если F(x) – какая-нибудь первообразная для f(x) , то
где C — произвольная постоянная (константа).
Для понимания смысла множества первообразных функции как неопределённого интеграла уместна следующая аналогия. Пусть есть дверь (традиционная деревянная дверь). Её функция — «быть дверью». А из чего сделана дверь? Из дерева. Значит, множеством первообразных подынтегральной функции «быть дверью», то есть её неопределённым интегралом, является функция «быть деревом + С», где С — константа, которая в данном контексте может обозначать, например, породу дерева. Подобно тому, как дверь сделана из дерева при помощи некоторых инструментов, производная функции «сделана» из первообразной функции при помощи формулы, которую мы узнали, изучая производную.
Тогда таблица функций распространённых предметов и соответствующих им первообразных («быть дверью» — «быть деревом», «быть ложкой» — «быть металлом» и др.) аналогична таблице основных неопределённых интегралов, которая будет приведена чуть ниже. В таблице неопределённых интегралов перечисляются распространённые функции с указанием первообразных, из которых «сделаны» эти функции. В части задач на нахождение неопределённого интеграла даны такие подынтегральные функции, которые без особых услилий могут быть проинтегрированы непосредственно, то есть по таблице неопределённых интегралов. В задачах посложнее подынтегральную функцию нужно предварительно преобразовать так, чтобы можно было использовать табличные интегралы.
Факт 2. Восстанавливая функцию как первообразную, мы должны учитывать произвольную постоянную (константу) C, а чтобы не писать список первообразной с различными константами от 1 до бесконечности, нужно записывать множество первообразных с произвольной константой C, например, так: 5x³+С . Итак, произвольная постоянная (константа) входит в выражение первообразной, поскольку первообразная может быть функцией, например, 5x³+4 или 5x³+3 и при дифференцировании 4 или 3, или любая другая константа обращаются в нуль.
Поставим задачу интегрирования: для данной функции f(x) найти такую функцию F(x), производная которой равна f(x).
Пример 1.Найти множество первообразных функции
Решение. Для данной функции первообразной является функция
Функция F(x) называется первообразной для функции f(x), если производная F(x) равна f(x), или, что одно и то же, дифференциал F(x) равен f(x) dx, т.е.

Следовательно, функция 


где С – произвольная постоянная. В этом можно убедиться дифференцированием.
Таким образом, если для функции существует одна первообразная, то для неё существует бесконечное множество первообразных, отличающихся на постоянное слагаемое. Все первообразные для функции 
Теорема (формальное изложение факта 2). Если F(x) – первообразная для функции f(x) на некотором промежутке Х, то любая другая первообразная для f(x) на том же промежутке может быть представлена в виде F(x) + C , где С – произвольная постоянная.
В следующем примере уже обращаемся к таблице интегралов, которая будет дана в параграфе 3, после свойств неопределённого интеграла. Делаем это до ознакомления со всей таблицей, чтобы была понятна суть вышеизложенного. А после таблицы и свойств будем пользоваться ими при интегрировании во всей полносте.
Пример 2. Найти множества первообразных функций:
1)
2)
3)
Решение. Находим множества первообразных функций, из которых «сделаны» данные функции. При упоминании формул из таблицы интегралов пока просто примите, что там есть такие формулы, а полностью саму таблицу неопределённых интегралов мы изучим чуть дальше.
1) Применяя формулу (7) из таблицы интегралов при n = 3, получим
2) Используя формулу (10) из таблицы интегралов при n = 1/3, имеем
то по формуле (7) при n = -1/4 найдём
Под знаком интеграла пишут не саму функцию f , а её произведение на дифференциал dx . Это делается прежде всего для того, чтобы указать, по какой переменной ищется первообразная. Например,


здесь в обоих случаях подынтегральная функция равна 
Процесс нахождения неопределённого интеграла функции называется интегрированием этой функции.
Геометрический смысл неопределённого интеграла
Пусть требуется найти кривую y=F(x) и мы уже знаем,что тангенс угла наклона касательной в каждой её точке есть заданная функция f(x) абсциссы этой точки.
Согласно геометрическому смыслу производной, тангенс угла наклона касательной в данной точке кривой y=F(x) равен значению производной F'(x). Значит, нужно найти такую функцию F(x), для которой F'(x)=f(x). Требуемая в задаче функция F(x) является первообразной от f(x). Условию задачи удовлетворяет не одна кривая, а семейство кривых. y=F(x) — одна из таких кривых, а всякая другая кривая может быть получена из неё параллельным переносом вдоль оси Oy.
Назовём график первообразной функции от f(x) интегральной кривой. Если F'(x)=f(x), то график функции y=F(x) есть интегральная кривая.
Факт 3. Неопределённый интеграл геометрически представлен семеством всех интегральных кривых , как на рисунке ниже. Удалённость каждой кривой от начала координат определяется произвольной постоянной (константой) интегрирования C.
Свойства неопределённого интеграла
Факт 4. Теорема 1. Производная неопределённого интеграла равна подынтегральной функции, а его дифференциал – подынтегральному выражению.
Факт 5. Теорема 2. Неопределённый интеграл от дифференциала функции f(x) равен функции f(x) с точностью до постоянного слагаемого , т.е.

Теоремы 1 и 2 показывают, что дифференцирование и интегрирование являются взаимно-обратными операциями.
Факт 6. Теорема 3. Постоянный множитель в подынтегральном выражении можно выносить за знак неопределённого интеграла , т.е.

Факт 7. Теорема 4. Неопределённый интеграл алгебраической суммы конечного числа функций равен алгебраической сумме неопределённых интегралов этих функций , т.е.

Таблица основных неопределённых интегралов
Факт 8. Пользусь таблицей неопределённых интегралов, свойствами неопределённого интеграла и методами интегрирования, можно отыскать неопределённый интеграл любой функции.
Из определения неопределённого интеграла вытекают следующие формулы, которые в дальнейшем будем называть табличными интегралами:
(6)
(7)
(8)
(9)
(10)
(11)
(12)
(13)
(14)
(15)
(16)
(17)
(18)
(19)
(20)
(21)
(22)
(23)
(24)
(25)
http://abudnikov.ru/studentam/matematicheskij-analiz/integralnoe-ischislenie-funkczij-odnoj-peremennoj/prostejshie-neopredelyonnyie-integralyi.html
http://function-x.ru/integral01.html
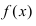
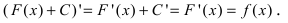
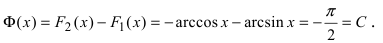
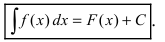
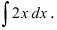
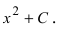
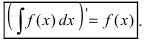
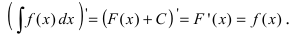
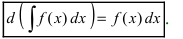
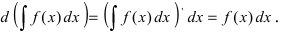
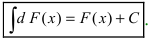
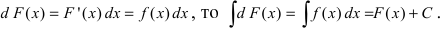
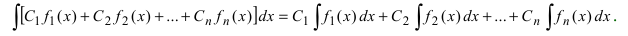
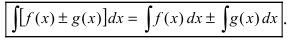
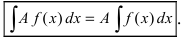
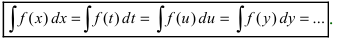
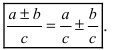
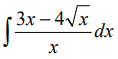
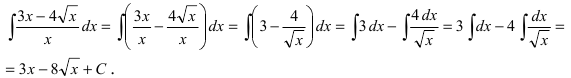
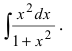
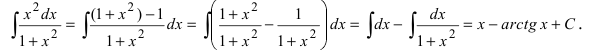
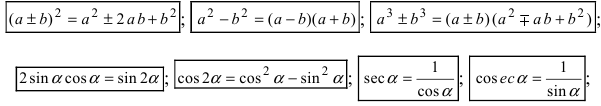
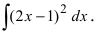
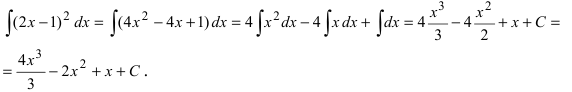
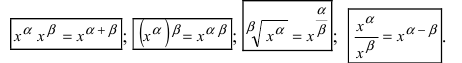
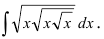
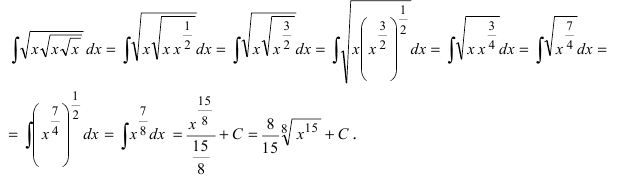
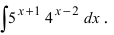
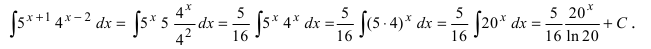
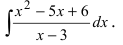
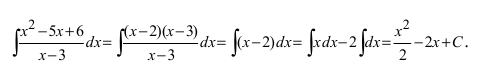
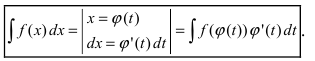
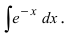
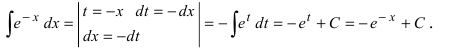
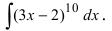
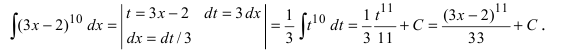
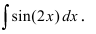
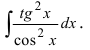
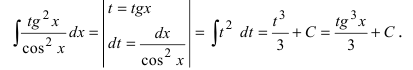
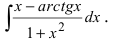
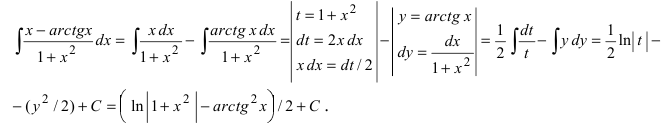
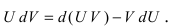
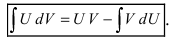
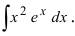
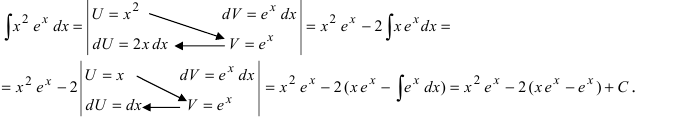
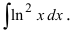
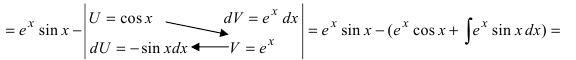
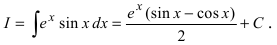
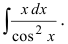
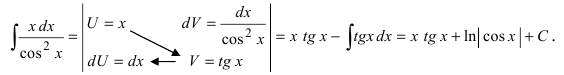
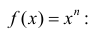
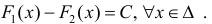
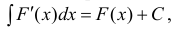 (3) или
(3) или 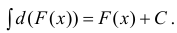
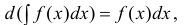 (4) здесь под записью
(4) здесь под записью 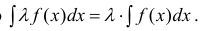 (5)
(5) имеют первообразную на Δ , тогда
имеют первообразную на Δ , тогда  также имеет первообразную на Δ и:
также имеет первообразную на Δ и: 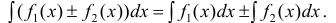 (6)
(6)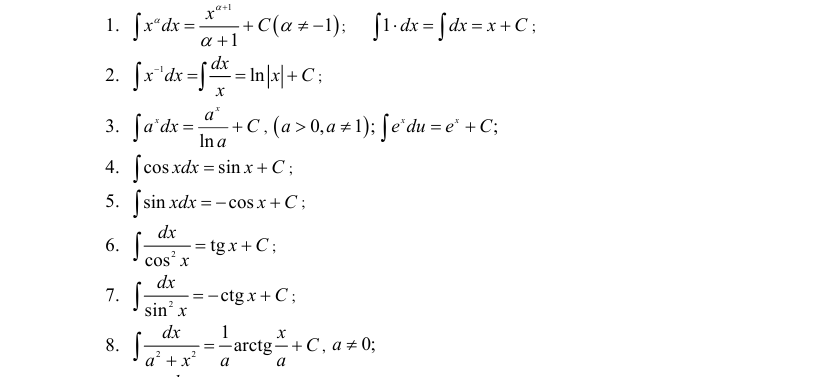
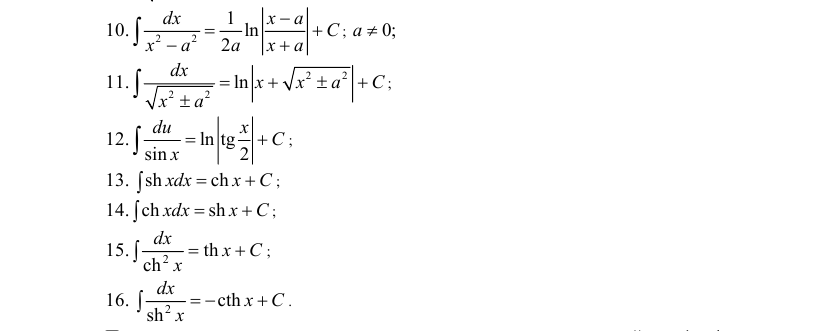
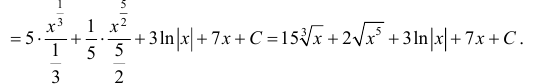
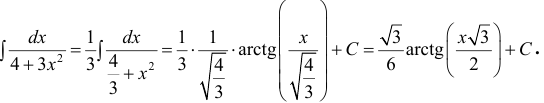
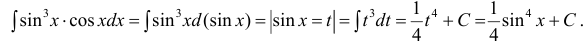
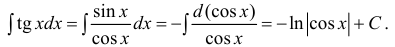
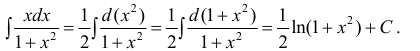
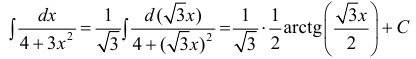
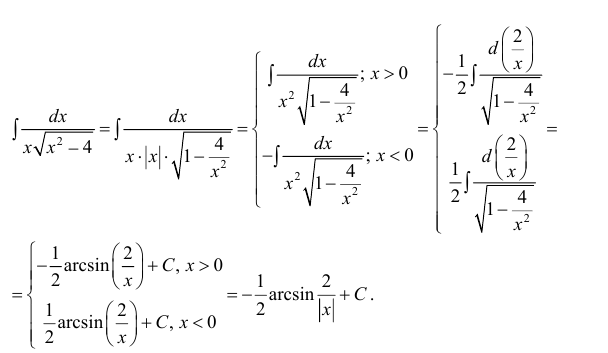
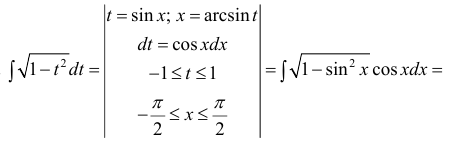
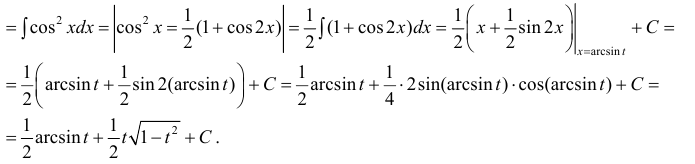
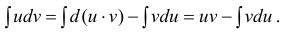
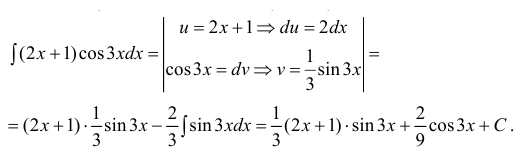
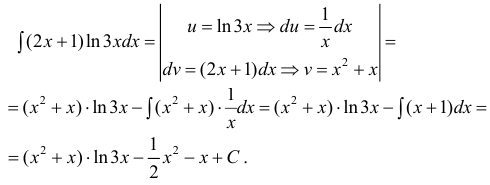
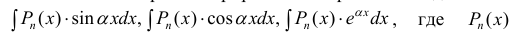 — многочлен степени n полагают:
— многочлен степени n полагают: 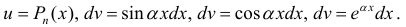 После интегрирования по частям степень многочлена уменьшается на 1 (см. пример 1).
После интегрирования по частям степень многочлена уменьшается на 1 (см. пример 1).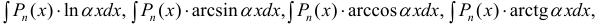
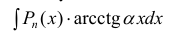 полагают:
полагают: 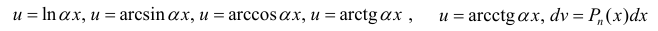 (
(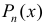 — многочлен). После интегрирования по частям интеграл упрощается.
— многочлен). После интегрирования по частям интеграл упрощается.