Извлечение корня из комплексного числа
Третий урок по комплексным числам. В этом уроке вы узнаете:
Начнём с ключевого определения.
1. Определение комплексного корня
Определение. Корнем $n$-й степени из комплексного числа $z$, где $n\in \mathbb
$, $n \gt 1$, называется такое комплексное число $\omega $, что
т.е. $n$-я степень числа $\omega $ равна $z$.
Таких корней на множестве комплексных чисел всегда будет ровно $n$ штук. Все они обозначаются привычным знаком радикала:
Пример. Вычислить $\sqrt[3]<-1>$ на множестве комплексных чисел.
Очевидно, привычная нам единица является таким корнем, потому что $<<\left( -1 \right)>^<3>>=-1$. Но есть ещё два корня:
Итого три корня. Как и предполагалось.
Теорема. Для любого комплексного числа $z\ne 0$ существует ровно $n$ комплексных чисел, каждое из которых является корнем $n$-й степени из числа $z.$
Все эти корни считаются по следующей формуле.
2. Формула корней
Теорема. Пусть комплексное число записано в тригонометрической форме:
\[z=\left| z \right|\cdot \left( \cos \varphi +i\sin \varphi \right)\]
Тогда все корни степени $n$ из этого числа можно найти по формуле:
По сути, эта теорема является обратной к формуле Муавра:
Почему степень всегда одна, а корней несколько — об этом в конце урока. Сейчас для нас главное — алгоритм извлечения корня из комплексного числа. Он состоит из четырёх шагов:
- Перевести комплексное число в тригонометрическую форму;
- Записать общую формулу корня степени $n$;
- Подставить в эту формулу $k=0$, затем $k=1$ и так до $k=n-1$.
- Получим $n$ комплексных корней. Вместе они и будут ответом.
В ответе всегда будет набор из $n$ чисел. Потому что невозможно однозначно извлечь корень из комплексного числа $z\ne 0$.
Представим число $-8i$ в тригонометрической форме:
\[\begin
Запишем формулу корней в общем виде:
\[\sqrt[3]<-8i>=2\cdot \left( \cos \left( -\frac<\pi > <6>\right)+i\sin \left( -\frac<\pi > <6>\right) \right)=\sqrt<3>-i\]
В ответе нужно указать все три числа: $-2i$; $\sqrt<3>-i$; $-\sqrt<3>-i$.
Ещё раз: подставляя разные $k$, мы будем получать разные корни. Всего таких корней будет ровно $n$. А если взять $k$ за пределами диапазона $\left\< 0,1. n-1 \right\>$, то корни начнут повторяться, и ничего нового мы не получим.
3. Геометрическая интерпретация
Если отметить на комплексной плоскости все значения корня $n$-й степени из некоторого комплексного числа $z\ne 0$, то все они будут лежать на окружности с центром в начале координат и радиусом $R=\sqrt[n]<\left| z \right|>$. Более того: эти точки образуют правильный $n$-угольник.
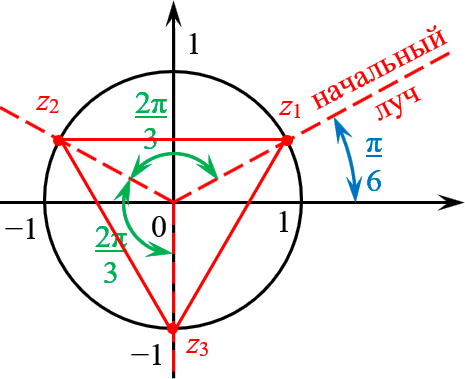
Отметить на комплексной плоскости все числа вида $\sqrt[3]$.
Представим число $z=i$ в тригонометрической форме:
\[\begin
Формула комплексных корней:
\[\sqrt[3]
Это три точки $<
Получили правильный треугольник. Его первая вершина лежит на пересечении окружности радиуса 1 и начального луча, который образован поворотом оси $OX$ на угол $<\pi >/<6>\;$.
Рассмотрим более сложный пример:
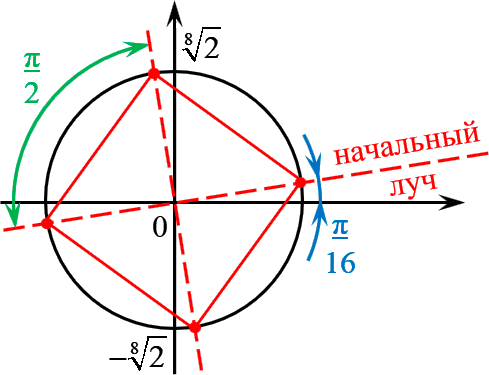
Отметить на комплексной плоскости все числа вида $\sqrt[4]<1+i>$.
Сразу запишем формулу корней с выделением начального луча:
\[\sqrt[4]
Отмечаем эти точки на комплексной плоскости. Радиус окружности $R=\sqrt[8]<2>$, начальный луч $<\pi >/<16>\;$:
И вновь всё чётко: четыре точки — правильный четырёхугольник, т.е. квадрат. С отклонением начального луча $<\pi >/<16>\;$.
Ну и ещё один пример — вновь без промежуточных вычислений. Только формулировка задачи, формула корней и окончательный чертёж:
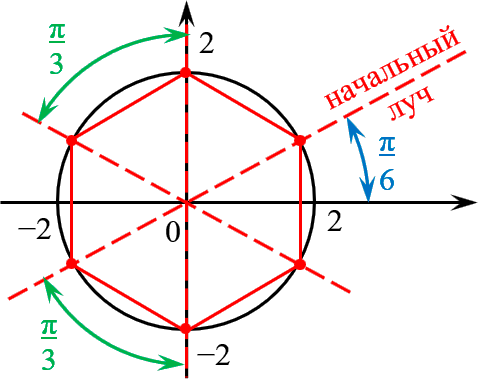
Отметить на комплексной плоскости все числа вида $\sqrt[6]<-64>$.
Формула корней с выделением начального луча:
\[\sqrt[6]
Получили правильный шестиугольник со стороной 2 и начальным лучом $<\pi >/<6>\;$.
Таким образом, мы получаем «графический» алгоритм извлечения корня $n$-й степени из комплексного числа $z\ne 0$:
- Перевести число в тригонометрическую форму;
- Найти модуль корня: $\sqrt[n]<\left| z \right|>$ — это будет радиусом окружности;
- Построить начальный луч с отклонением $\varphi =<\arg \left( z \right)>/
\;$; - Построить все остальные лучи с шагом $<2\pi >/
\;$; - Получим точки пересечения лучей с окружностью — это и есть искомые корни.
Такой алгоритм прекрасно работает, когда аргумент исходного числа и отклонение начального луча $\varphi $ — стандартные «табличные» углы вроде $<\pi >/<6>\;$. На практике чаще всего именно так и бывает. Поэтому берите на вооружение.:)
4. Почему корней всегда ровно n
С геометрической точки зрения, всё очевидно: если мы будем последовательно зачёркивать вершины правильного $n$-угольника, то ровно через $n$ шагов все вершины будут зачёркнуты. И для дальнейшего зачёркивания придётся выбирать вершину среди уже зачёркнутых.
Однако рассмотрим проблему с точки зрения алгебры. Ещё раз запишем формулу корня $n$-й степени:
Последовательно подставим в эту формулу указанные значения параметра $k$:
Очевидно, последняя строка получена при $k=n-1$. Подставим теперь $k=n$:
Поскольку синус и косинус — периодические функции с периодом $2\pi $, $<<\omega >_
5. Выводы
Ключевые факты из урока.
Определение. Корень степени $n$ из комплексного числа $z$ — это такое число $\omega $, что $<<\omega >^
>=z$.
Обозначение. Для обозначения комплексных корней используется знакомый знак радикала: $\omega =\sqrt[n]
Замечание. Если $z\ne 0$, таких чисел корней будет ровно $n$ штук.
Алгоритм нахождения корней состоит из двух шагов.
Шаг 1. Представить исходное число в тригонометрической форме:
\[z=\left| z \right|\cdot \left( \cos \varphi +i\sin \varphi \right)\]
Шаг 2. Воспользоваться формулой Муавра для вычисления корней:
Все полученные корни лежат на окружности радиуса $\sqrt[n]<\left| z \right|>$ с центром в начале координат и являются вершинами правильного $n$-угольника. Первая вершина лежит на т.н. «начальном луче», который отклонён от положительной полуоси $OX$ на угол $<\varphi >/
Геометрическую интерпретацию можно использовать для быстрого «графического» извлечения корней. Но это требует практики и хорошего понимания, что именно и зачем вы делаете. Технология такого извлечения корней описана выше в разделе «Геометрическая интерпретация».
Всё. В следующем уроке начнём решать уравнения в комплексных числах.:)
Извлечение корней: методы, способы, решения
Из этой статьи вы узнаете:
- что такое «извлечение корня»;
- в каких случаях он извлекается;
- принципы нахождения значения корня;
- основные способы извлечения корня из натуральных и дробных чисел.
Что такое «извлечение корня»
Для начала введем определение «извлечение корня».
Извлечение корня — процесс нахождения значения корня.
При извлечении корня n -ной степени из числа a, мы находим число b , n -ная степень которого равняется a . Если мы нашли такое число b , можно утверждать, что корень извлечен.
Выражения «извлечение корня» и «нахождение значения корня» равнозначны.
В каких случаях извлекается корень?
Корень n -ной степени можно извлечь из числа a точно в случае, если a можно представить в виде n -ной степени некоторого числа b .
4 = 2 × 2 , следовательно, из числа 4 можно точно извлечь квадратный корень, который равен 2
Когда корень n -ной степени из числа a невозможно представить в виде n -ной степени числа b , то такой корень не извлекается, либо извлекается только приближенное значение корня с точностью до любого десятичного разряда.
Принципы нахождения значения корня и способы их извлечения
- Использование таблицы квадратов, таблицы кубов и т.д.
- Разложение подкоренного выражения (числа) на простые множители
- Извлечение корней из дробных чисел
- Извлечение корня из отрицательного числа
- Поразрядное нахождение значения корня
Необходимо понять, по каким принципам находится значение корней, и каким образом они извлекаются.
Главный принцип нахождения значения корней — основываться на свойствах корней, в том числе на равенстве: b n n = b , которое является справедливым для любого неотрицательного числа b .
Начать следует с наиболее простого и очевидного способа: таблицы квадратов, кубов и т.д.
Когда таблицы под руками нет, вам поможет способ разложения подкоренного числа на простые множители (способ незатейливый).
Стоит уделить внимание извлечению корня из отрицательного числа, что является возможным для корней с нечетными показателями.
Изучим, как извлекать корни из дробных чисел, в том числе из смешанных чисел, обыкновенных и десятичных дробей.
И потихоньку рассмотрим способ поразрядного нахождения значения корня — наиболее сложного и многоступенчатого.
Использование таблицы квадратов, кубов и т.д.
Таблица квадратов включает в себя все числа от 0 до 99 и состоит из 2 зон: в первой зоне можно составить любое число до 99 с помощью вертикального столбца с десятками и горизонтальной строки с единицами, во второй зоне содержатся все квадраты образуемых чисел.
Таблица квадратов
| Таблица квадратов | единицы | ||||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||
| десятки | 0 | 0 | 1 | 4 | 9 | 16 | 25 | 36 | 49 | 64 | 81 |
| 1 | 100 | 121 | 144 | 169 | 196 | 225 | 256 | 289 | 324 | 361 | |
| 2 | 400 | 441 | 484 | 529 | 576 | 625 | 676 | 729 | 784 | 841 | |
| 3 | 900 | 961 | 1024 | 1089 | 1156 | 1225 | 1296 | 1369 | 1444 | 1521 | |
| 4 | 1600 | 1681 | 1764 | 1849 | 1936 | 2025 | 2116 | 2209 | 2304 | 2041 | |
| 5 | 2500 | 2601 | 2704 | 2809 | 2916 | 3025 | 3136 | 3249 | 3364 | 3481 | |
| 6 | 3600 | 3721 | 3844 | 3969 | 4096 | 4225 | 4356 | 4489 | 4624 | 4761 | |
| 7 | 4900 | 5041 | 5184 | 5329 | 5476 | 5625 | 5776 | 5929 | 6084 | 6241 | |
| 8 | 6400 | 6561 | 6724 | 6889 | 7056 | 7225 | 7396 | 7569 | 7744 | 7921 | |
| 9 | 8100 | 8281 | 8464 | 8649 | 8836 | 9025 | 9216 | 9409 | 9604 | 9801 | |
Существуют также таблицы кубов, четвертой степени и т.д., которые созданы по принципу, аналогичному таблице квадратов.
Таблица кубов
| Таблица кубов | единицы | ||||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||
| десятки | 0 | 0 | 1 | 8 | 27 | 64 | 125 | 216 | 343 | 512 | 729 |
| 1 | 1000 | 1 331 | 1 728 | 2 197 | 2 744 | 3 375 | 4 096 | 4 913 | 5 832 | 6 859 | |
| 2 | 8000 | 9 261 | 10 648 | 12 167 | 13 824 | 15 625 | 17 576 | 19 683 | 21 952 | 24 389 | |
| 3 | 27000 | 29 791 | 32 768 | 35 937 | 39 304 | 42 875 | 46 656 | 50 653 | 54 872 | 59 319 | |
| 4 | 64000 | 68 921 | 74 088 | 79 507 | 85 184 | 91 125 | 97 336 | 103 823 | 110 592 | 117 649 | |
| 5 | 125000 | 132 651 | 140 608 | 148 877 | 157 464 | 166 375 | 175 616 | 185 193 | 195 112 | 205 379 | |
| 6 | 216000 | 226 981 | 238 328 | 250 047 | 262 144 | 274 625 | 287 496 | 300 763 | 314 432 | 328 509 | |
| 7 | 343000 | 357 911 | 373 248 | 389 017 | 405 224 | 421 875 | 438 976 | 456 533 | 474 552 | 493 039 | |
| 8 | 512000 | 531 441 | 551 368 | 571 787 | 592 704 | 614 125 | 636 056 | 658 503 | 681 472 | 704 969 | |
| 729000 | 753 571 | 778 688 | 804 357 | 830 584 | 857 375 | 884 736 | 912 673 | 941 192 | 970 299 | ||
Принцип функционирования таких таблиц прост, однако их часто нет под рукой, что значительно усложняет процесс извлечение корня, поэтому необходимо владеть минимум несколькими способами извлечения корней.
Разложение подкоренного числа на простые множители
Наиболее удобный способ нахождения значения корня после таблицы квадратов и кубов.
Способ разложения подкоренного числа на простые множители подразумевает под собой представление числа в виде степени с необходимым показателем, что дает нам возможность получить значение корня.
Извлечем квадратный корень из 144 .
Разложим 144 на простые множители:
Таким образом: 144 = 2 × 2 × 2 × 2 × 3 × 3 = ( 2 × 2 ) 2 × 3 2 = ( 2 × 2 × 3 ) 2 = 12 2 . Следовательно, 144 = 12 2 = 12 .
Также при использовании свойств степени и корней можно записать преобразование немного по-другому:
144 = 2 × 2 × 2 × 2 × 3 × 3 = 2 4 × 3 2 = 2 4 × 3 2 = 2 2 × 3 = 12
144 = 12 — окончательный ответ.
Извлечение корней из дробных чисел
Запоминаем: любое дробное число должно быть записано в виде обыкновенной дроби.
Следуя свойству корня из частного, справедливым является следующее равенство:
p q n = p n q n . Исходя из этого равенства, необходимо воспользоваться правилом извлечения корня из дроби: корень из дроби равен от деления корня числителя на корень знаменателя.
Рассмотрим пример извлечения корня из десятичной дроби, поскольку извлечь корень из обыкновенной дроби можно с помощью таблицы.
Необходимо извлечь кубический корень из 474 , 552 . Первым делом, представим десятичную дробь в виде обыкновенной: 474 , 552 = 474552 / 1000 . Из этого следует: 474552 1000 3 = 474552 3 1000 3 . Затем можно приступить к процессу извлечения кубических корней в числителе и знаменателе:
474552 = 2 × 2 × 2 × 3 × 3 × 3 × 13 × 13 × 13 = ( 2 × 3 × 13 ) 3 = 78 3 и 1000 = 10 3 , то
474552 3 = 78 3 3 = 78 и 1000 3 = 10 3 3 = 10 .
Завершаем вычисления: 474552 3 1000 3 = 78 10 = 7 , 8 .
Извлечение корня из отрицательных чисел
Если знаменатель является нечетным числом, то число под знаком корня может оказаться отрицательным. Из этого следует: для отрицательного числа — a и нечетного показателя корня 2 n — 1 справедливо равенство:
— a 2 × n — 1 = — a 2 × n — 1
Правило извлечения нечетной степени из отрицательных чисел: чтобы извлечь корень из отрицательного числа необходимо извлечь корень из противоположного ему положительного числа и поставить перед ним знак минус.
— 12 209 243 5 . Для начала необходимо преобразовать выражение, чтобы под знаком корня оказалось положительно число:
— 12 209 243 5 = 12 209 243 — 5
Затем следует заменить смешанное число обыкновенной дробью:
12 209 243 — 5 = 3125 243 — 5
Пользуясь правилом извлечения корней из обыкновенной дроби, извлекаем:
3125 243 — 5 = — 3125 5 243 5
Вычисляем корни в числителе и знаменателе:
— 3125 5 243 5 = — 5 5 5 3 5 5 = — 5 3 = — 1 2 3
Краткая запись решения:
— 12 209 243 5 = 12 209 243 — 5 = 3125 243 — 5 = — 3125 5 243 5 = — 5 5 5 3 5 5 = — 5 3 = — 1 2 3 .
Ответ: — 12 209 243 5 = — 1 2 3 .
Поразрядное нахождение значения корня
Бывают случаи, когда под корнем находится число, которое не получается представить в виде n — ной степени некоторого числа. Но необходимо знать значение корня с точностью до некоторого знака.
В таком случае необходимо воспользоваться алгоритмом поразрядного нахождения значения корня, с помощью которого можно получить достаточное количество значений искомого числа.
Как это происходит, разберем на примере извлечения квадратного корня из 5 .
Сперва необходимо найти значение разряда единиц. Для этого начнем перебирать значения 0 , 1 , 2 , . . . , 9 , вычисляя при этом 0 2 , 1 2 , . . . , 9 2 до необходимого значения, которое больше, чем подкоренное число 5 . Все это удобно представить в виде таблицы:
| Возможное значение корня | 0 | 1 | 2 | 3 |
| Это значение в степени | 0 | 1 | 4 | 9 |
Значение ряда единиц равняется 2 ( т а к к а к 2 2 5 , а 2 3 > 5 ) . Переходим в разряду десятых — будем возводить в квадрат числа 2 , 0 , 2 , 1 , 2 , 2 , . . . , 2 , 9 , , сравнивая полученные значения с числом 5 .
| Возможное значение корня | 2,0 | 2,1 | 2,2 | 2,3 |
| Это значение в степени | 4 | 4,41 | 4,84 | 5,29 |
Поскольку 2 , 2 2 5 , а 2 , 3 2 > 5 , то значение десятых равняется 2 . Переходим к нахождению значения сотых:
| Возможное значение корня | 2.20 | 2,21 | 2,22 | 2,23 | 2,24 |
| Это значение в степени | 4,84 | 4,8841 | 4,8294 | 4,9729 | 5,0176 |
Таким образом, найдено значение корня из пяти — 2 , 23 . Можно находить значения корня дальше:
2 , 236 , 2 , 2360 , 2 , 23606 , 2 , 236067 , . . .
Итак, мы изучили несколько наиболее распространенных способов нахождения значения корня, воспользоваться которыми можно в любой ситуации.
Числа. Извлечение корней из комплексных чисел. Квадратное уравнение с комплексными корнями.
Рассматривать будем на таком примере:
Если говорить о действительных числах, то, вы знаете, что корень из отрицательного числа нельзя извлекать. Однако в комплексных числах можно. Если конкретнее, 2 корня:
Выполним проверку того, что эти корни и права оказываются решением уравнения:
Что и требовалось доказать.
Зачастую используют сокращенную запись, корни записывают в одну строчку в таком виде: 
Такие корни являются сопряженными комплексными корнями.
Теперь вы знаете как можно извлечь квадратный корень из отрицательного числа. Приведем еще несколько примеров:




В каждом случае получаем 2 сопряженных комплексных корня.
Решим квадратное уравнение 
Первым шагом определим дискриминант уравнения:
В нашем случае дискриминант оказался отрицательным, и в случае с действительными числами у уравнения нет решений, но у нас вариант с комплексными числами, поэтому можем продолжать решение:
Как известно из формул дискриминанта у нас образуется 2 корня:

Т.о., у уравнения 

Теперь можно решить любое квадратное уравнение!
У любого уравнения с многочленом n-ой степени 
Как извлечь корень из произвольного комплексного числа?
Рассмотрим уравнение z n = w, либо, записав в другом виде: 
В частности, при n = 2 получаем квадратный корень 
У уравнения типа 

где 
φ – его аргумент,
а параметр k принимает значения: 
Найдем корни уравнения: 
Перепишем уравнение как: 
В этом примере 



Далее найдем модуль и аргумент комплексного числа 
Число w находится в 1-ой четверти, значит:
Помним, что определяя тригонометрическую форму комплексного числа лучше делать чертеж.
Детализируем еще немного общую формулу:


Так подобно расписывать не обязательно. Здесь мы это сделали, что бы было ясно откуда что образовалось.
Подставляем в формулу значение k = 0 и получаем 1-й корень:

Подставляем в формулу значение k = 1 и получаем 2-й корень:

Ответ: 
Если необходимо, корни, которые мы получили можно перевести обратно в алгебраическую форму.
Часто вычисленные корни нужно изобразить геометрически:
Как выполнить чертеж?
Для начала на калькуляторе вычисляем, чему равен модуль корней 
Далее берем аргумент 1-го корня 

Отмеряем транспортиром 45° и ставим на чертеже точку z0.
Берем аргумент 2-го корня 

По этому же алгоритму ставим точку z2.
Видно, что корни располагаются геометрически правильно с интервалом 
http://zaochnik.com/spravochnik/matematika/korni/izvlechenie-kornej/
http://www.calc.ru/Chisla-Izvlecheniye-Korney-Iz-Kompleksnykh-Chisel-Kvadratnoy.html