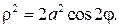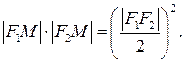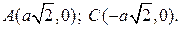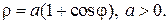Уравнение кардиоиды в параметрическом виде
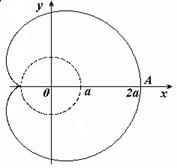
Кардиоида – плоская кривая, описываемая произвольной точкой М окружности радиуса r, катящейся без проскальзывания извне по другой, неподвижной, окружности того же радиуса – см. рис.
Кардиоида – частный случай эпициклоиды, одна из конхоид и улиток Паскаля.
Если над параболой выполнить преобразование инверсии с центром в фокусе параболы, то парабола перейдет в кардиоиду.
В прямоугольной декартовой системе координат кардиоиду можно задать уравнением
(x 2 + y 2 – 2rx) 2 = 4r 2 (x 2 + y 2 ),
где r – радиус окружности.
Как видно из уравнения, она является алгебраической кривой четвертого порядка и симметрична относительно оси абсцисс. Точка – точка возврата первого рода. Длина l дуги кардиоиды от точки K до точки М может быть вычислена по формуле
l = 16rsin 2 (φ/2),
a площадь, ограниченная кардиоидой, равна 6πr 2 .
Уравнение кардиоиды в полярных координатах (с полюсом на неподвижной окружности) имеет вид:
ρ = 2r(1 + cosφ).
Параметрические уравнения кардиоиды могут выглядеть так:
x = 2rcost – rcos2t; y = 2rsint – rsin2t.
Название кардиоиды происходит от греческих слов χαρδια – сердце, и ειδος – вид, вместе – сердцевидная.
Уравнения кривых. Кардиоида. Улитка Паскаля.
Если применить две окружности с равными радиусами и вращать одну вокруг другой, то образуется кардиоида(греч. кардиа — сердце) — математики считают, что сформированная кривая отдаленно схожа с сердцем.
Если брать точку не на самой катящейся окружности, а внутри ее, сместив в сторону от центра, тогда будет образована кривая, получившая название Улитка Паскаля или лимакона.
Пусть a – диаметр исходной окружности, а l — расстояние, на которое смещается точка вдоль радиус – вектора. Тогда возможны такие варианты улитки Паскаля: а > l, a = l и a 2 + у 2 +2аx) 2 – 4a 2 (х 2 + у 2 ) = 0;
в полярных координатах:
В прямоугольных координатах (параметрическая запись):
x = 2a cos t – a cos 2t;
Длина дуги одного витка кардиоиды, определяется формулой:
Площадь фигуры, ограниченной кардиоидой, определяется формулой:
.
Улитка Паскаля характеризуется уравнениями:
Площадь, ограниченная улиткой Паскаля:
.
При а > l площадь внутренней петли при вычислении по этой формуле считается дважды.
Уравнение окружности в параметрическом виде
Кардиоида
Лемниската Бернулли
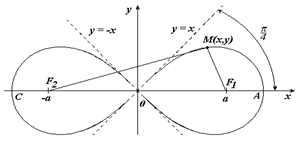
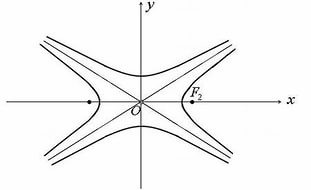
Лемниската Бернулли – линия, представляющая геометрическое место точек, расстояние которых от двух данных точек (фокусов) есть постоянная величина, равная квадрату половины межфокусного расстояния.
В полярных координатах
Укажем, что точка М лежит на кривой, если выполнено условие
Вершины кривой находятся в точках
Площадь каждой петли S=a 2 .
В полярных координатах
Вершина кардиоиды находится в точке А(2а,0).
Укажем, что площадь кардиоиды 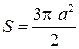
6. Параметрическое задание линий
Параметрические уравнения линий задаются в виде зависимости текущих координат x и y от некоторого параметра t. Каждому значению t соответствуют два значения: x и y. При изменении параметра t текущая точка M(x,y) описывает некоторую кривую на плоскости.
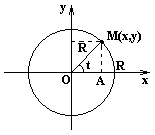 |
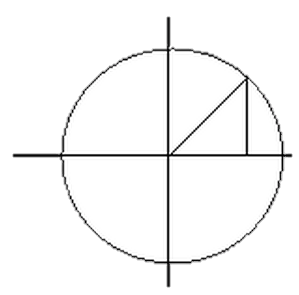
Пусть M(x,y) – текущая точка окружности с центром в начале координат и радиусом R. В качестве параметра t выберем угол, который составляет радиус-вектор точки М с осью ox 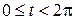
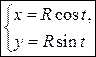
Исключим из параметрических уравнений параметр t. Для этого возведём эти уравнения в квадрат и сложим их:
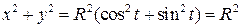
| | | следующая лекция ==> | |
| Четырехлепестковые розы | | | Астроида |
Дата добавления: 2013-12-13 ; Просмотров: 2896 ; Нарушение авторских прав? ;
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Параметрическое представление — используемая в математическом анализе разновидность представления переменных, когда их зависимость выражается через дополнительную величину — параметр.
Содержание
Параметрическое представление функции [ править | править код ]
Предположим, что функциональная зависимость y от x не задана непосредственно y = f(x), а через промежуточную величину — t. Тогда формулы
;> 
задают параметрическое представление функции одной переменной.
Если предположить, что обе эти функции φ и ψ имеют производные и для φ существует обратная функция θ, явное представление функции выражается через параметрическое как [1] :
y = ψ ( θ ( x ) ) = f ( x )
и производная функции может быть вычислена как
y ′ ( x ) = d y d x = y t ′ x t ′ = ψ ′ ( t ) ϕ ′ ( t ) >= >>= >
Параметрическое представление даёт такое важное преимущество, что позволяет изучать неявные функции в тех случаях, когда их приведение к явному виду иначе как через параметры затруднительно.
Параметрическое представление уравнения [ править | править код ]
Параметрическое представление для более общего случая: когда переменные связаны уравнением (или системы уравнений, если переменных больше двух).
Параметрическое уравнение [ править | править код ]
Близкое понятие — параметрическое уравнение [2] множества точек, когда координаты точек задаются как функции от некоторого набора свободных параметров. Если параметр один, мы получим параметрическое уравнение кривой.
x = x ( t ) ; y = y ( t ) 

Выражая координаты точек поверхности через два свободных параметра, мы получим параметрическое задание поверхности.
Примеры [ править | править код ]
Уравнение окружности имеет вид:
x 2 + y 2 = r 2 . +y^ =r^ .>
Параметрическое уравнение окружности:
;> 
Параметрическое уравнение правой ветви гиперболы :
t> 
Предположим, что функция $x=phi (t)$ имеет обратную функцию $t= (x)$. Тогда справедливо равенство:
Параметрический способ задания функций широко применяется в механике. Так, если в плоскости некоторая материальная точка находится в движении (время $t$), и законы движения проекций этой точки на оси координат известны:
Уравнения являются параметрическими уравнениями траекторий движущейся точки. Исключая временной параметр, получим уравнение траектории в форме $y = f(x)$.
Определить траекторию и место падения груза, сброшенного с самолета, движущегося горизонтально со скорость $v_0$ на высоте $y_0$.
Допустим, что груз сбрасывается с момент пересечения самолетом оси Oy. Тогда очевидно, что горизонтальное перемещение груза равномерно и имеет постоянную скорость:
А вертикальное перемещение:
Следовательно, расстояние от груза до земли в произвольный момент падения:
Уравнения горизонтального и вертикального перемещения тела являются параметрическими. Для того, чтобы исключить временной параметр $t$, найдем его значение из первого уравнения.
Полученное выражение подставим во второе параметрическое уравнение чтобы найти уравнение траектории:
Попробуй обратиться за помощью к преподавателям
Уравнения некоторых кривых в параметрической форме:
- Окружность
Параметрические кривые окружности:
Рисунок 1. Окружность и ее параметрические кривые
Уравнение гиперболы имеет вид:
Параметрические кривые гиперболы:
Рисунок 2. Гипербола и ее параметрические кривые
Записать уравнение окружности в параметрическом виде.
- Представим уравнение окружности в виде: [x^ +y^ =r^ ] [x^ +y^ =6^ ]
Значит, радиус $r$ равен 6.
Задай вопрос специалистам и получи
ответ уже через 15 минут!
Записать уравнение гиперболы в параметрическом виде.
Так и не нашли ответ
на свой вопрос?
Просто напиши с чем тебе
нужна помощь
http://www.calc.ru/Uravneniya-Krivykh-Kardioida-Ulitka-Paskalya.html
http://4apple.org/uravnenie-okruzhnosti-v-parametricheskom-vide/