Касательная и нормаль к графику функции
Основные формулы
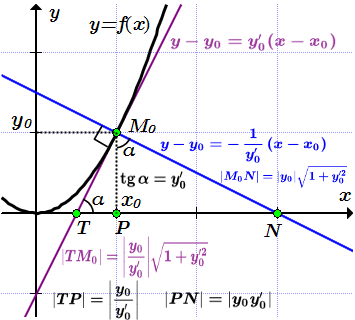
Пусть на некотором интервале X задана функция . Нас интересуют геометрические характеристики графика этой функции в некоторой заданной точке при значении аргумента , где . Пусть функция имеет в производную, которую будем обозначать как . Тогда через точку мы можем провести касательную к графику. Тангенс угла α между осью абсцисс x и касательной равен производной функции в точке :
(1) .
А само уравнение касательной имеет вид:
(2) .
В аналитической геометрии тангенс угла между прямой и осью абсцисс называют угловым коэффициентом прямой. Таким образом производная равна угловому коэффициенту касательной в .
См. Геометрический смысл производной
Прямая, перпендикулярная касательной, проведенной через точку , называется нормалью к графику функции в этой точке. Уравнение нормали имеет вид:
(3) .
См. Уравнение прямой с угловым коэффициентом ⇓
Пусть две кривые и пересекаются в точке . Тогда угол φ между касательными к этим кривым в точке называется углом между кривыми. Он определяется по формуле:
(4) , где .
Отсюда .
при .
Вывод формулы ⇓
Определения
Здесь мы приводим определения, которые встречаются в литературе, и имеют отношение к касательной и нормали. Вывод формул приводится в примере 1 ⇓.
Определение касательной приводится здесь. Уравнение касательной:
.
.
Отрезком касательной называют отрезок между точкой пересечения касательной с осью абсцисс и точкой .
.
Отрезком нормали называют отрезок между точкой пересечения нормали с осью абсцисс и точкой .
.
Подкасательной называют отрезок между точкой пересечения касательной с осью абсцисс и проекции точки на эту ось.
.
Поднормалью называют отрезок между точкой пересечения нормали с осью абсцисс и проекции точки на эту ось.
.
Углом между кривыми в точке их пересечения называют угол между касательными к кривым, проведенных через точку .
Полезные формулы из аналитической геометрии
Далее приводятся некоторые сведения из аналитической геометрии, которые могут оказаться полезными при решении задач.
Уравнение прямой, проходящей через две заданные точки и :
.
Здесь – направляющий вектор прямой.
Умножив это уравнение на , получим уравнение прямой в другом виде:
.
Здесь – вектор нормали прямой. Тогда само уравнение означает равенство нулю скалярного произведения векторов и .
Уравнение прямой, проходящей через точку параллельно вектору имеет вид:
.
Вектор называется направляющим вектором данной прямой. Это уравнение можно написать в параметрическом виде, введя параметр t :
Уравнение прямой, проходящей через точку перпендикулярно вектору имеет вид:
.
Вектор называется вектором нормали данной прямой.
Уравнение прямой с угловым коэффициентом k , проходящей через точку :
.
Угол α между прямой и осью x определяется по формуле:
.
Если две прямые взаимно перпендикулярны, то их угловые коэффициенты и связаны соотношением:
.
Уравнение прямой в отрезках, пересекающей оси координат в точках :
.
Примеры решения задач
Все примеры Ниже рассмотрены примеры решений следующих задач.
1. Найти уравнения касательной и нормали к кривой в точке . Найти длины отрезков касательной, нормали, подкасательной и поднормали. Решение ⇓
2. Составить уравнения касательной и нормали к циссоиде, заданной в параметрическом виде
, проведенных в точке . Решение ⇓
3. Заданной в неявном виде . Решение ⇓
4. Найти угол между кривыми и Решение ⇓
Пример 1
Составить уравнения касательной и нормали к кривой в точке . Найти длины отрезков касательной, нормали, подкасательной и поднормали.
Находим значение функции при :
.
Находим производную:
.
Находим производную в точке :
;
.
Находим уравнение касательной по формуле (2):
;
;
;
– уравнение касательной.
Строим касательную на графике. Поскольку касательная – это прямая, то нам нужно знать положения двух ее точек, и провести через них прямую.
При ;
при .
Проводим касательную через точки и .
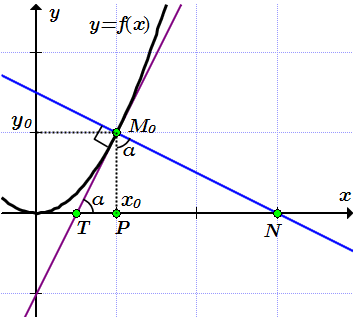
Найдем угол α между касательной и осью абсцисс по формуле (1):
.
Подставляем :
;
.
Находим уравнение нормали по формуле (3):
;
;
;
;
;
– уравнение нормали.
Строим нормаль по двум точкам.
При ;
при .
Проводим нормаль через точки и .
Находим длину отрезка касательной . Из прямоугольника имеем:
.
Поясним использованную формулу. Поскольку , то . Тогда
.
Подставляем :
.
Находим длину отрезка подкасательной . Из прямоугольника имеем:
.
Подставляем :
.
Находим длину отрезка нормали . Поскольку и , то треугольники и подобны. Тогда . Из прямоугольника имеем:
.
Подставляем :
.
Находим длину отрезка поднормали . Из прямоугольника имеем:
.
Примечание.
При выводе формул, можно сначала определить длины отрезков подкасательной и поднормали, а затем из прямоугольников, по теореме Пифагора, найти длины отрезков касательной и нормали:
;
.
Уравнение касательной: ; уравнение нормали: ;
длина отрезка касательной: ; длина отрезка нормали: ; длина подкасательной: ; длина поднормали: .
Пример 2
Составить уравнения касательной и нормали к циссоиде, заданной в параметрическом виде , проведенных в точке .
Находим значения переменных при .
;
.
Обозначим эту точку как .
Находим производные переменных x и y по параметру t .
;
;
;
;
.
Подставляя , находим производную y по x в точке .
.
Применяя формулу (2), находим уравнение касательной к циссоиде, проходящей через точку .
;
;
;
.
Применяя формулу (3), находим уравнение нормали к циссоиде в точке .
;
;
;
.
Уравнение касательной: .
Уравнение нормали: .
Пример 3
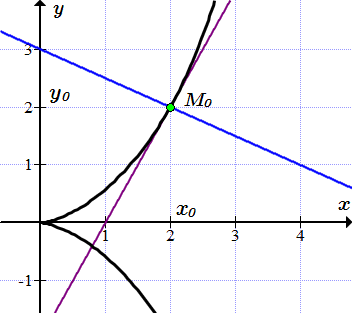
Составить уравнения касательной и нормали к циссоиде, заданной в неявном виде:
(П3) ,
проведенных в точке .
Для получения уравнение касательной и нормали, нам нужно знать значение производной функции в заданной точке. Функция (П3) задана неявно. Поэтому применяем правило дифференцирования неявной функции. Для этого дифференцируем (П3) по x , считая, что y является функцией от x .
;
;
;
.
Отсюда
.
Находим производную в заданной точке, подставляя .
;
.
Находим уравнение касательной по формуле (2).
;
;
;
.
Находим уравнение нормали по формуле (3).
;
;
;
.
Касательная и нормаль к циссоиде изображены на рисунке ⇑.
Уравнение касательной: .
Уравнение нормали: .
Пример 4
Найти угол между кривыми и .
Найдем множество точек пересечения кривых, решая систему уравнений.
Левые части равны. Приравниваем правые части и выполняем преобразования.
;
(П4) .
Поскольку функция строго монотонна, то уравнение (П4) имеет один корень:
.
При . Кривые пересекаются в единственной точке . Обозначим ее как , где .
Введем обозначения для функций, с помощью которых заданы кривые:
.
Найдем их производные.
;
.
Найдем значения производных в точке , подставляя .
;
.
Ниже приводятся графики функций ⇓ и вывод формулы угла между кривыми.
Вывод формулы для угла между кривыми
Изложим вывод формулы (4). Для иллюстрации используем только что рассмотренный пример ⇑, в котором .
Рассмотрим две кривые, заданные уравнениями и , и пересекающиеся в некоторой точке . Докажем, что угол между кривыми определяется по формуле (4):
, где .
Или ;
при .
Проведем касательные к графикам функций в точке . Углы, которые образуют касательные с осью x обозначим как и . За положительное направление выберем направление против часовой стрелки. На рисунке . Считаем, что значения углов принадлежат интервалам . Согласно геометрическому смыслу производной,
.
В аналитической геометрии принято, что угол φ между прямыми равен наименьшему значению угла между ними.
Если , то ;
если , то .
Таким образом величина угла φ между касательными может находиться только в пределах
(Ф2) .
На рисунке угол между лучами и больше 90°, а между лучами и – меньше. Поэтому .
При доказательстве мы будем использовать соотношение:
, которое выполняется при .
Тогда в силу (Ф2),
.
Случай мы рассмотрим отдельно.
1) Пусть .
Тогда угол между прямыми . И мы имеем:
.
В конце мы подставили (Ф1).
2) Пусть .
Тогда ; . Поэтому . Это можно записать так: . Также применим формулу: . В результате получаем:
.
Этот случай изображен на рисунке ⇑.
3) Пусть .
При этом касательные взаимно перпендикулярны, . В этом случае , что указано в (4).
Использованная литература:
П.Е. Данько, А.Г. Попов, Т.Я.Кожевникова. Высшая математика в упражнениях и задачах. Часть 1. Москва, Высшая школа, 1980.
Л.Д. Кудрявцев, А.Д. Кутасов, В.И. Чехлов, М.И. Шабунин. Сборник задач по математическому анализу. Том 1. Москва, Физматлит, 2003.
Автор: Олег Одинцов . Опубликовано: 30-06-2021
Уравнение касательной и уравнение нормали к графику функции
Как получить уравнение касательной и уравнение нормали
Касательная — это прямая, которая касается графика функции в одной точке и все точки которой находятся на наименьшем расстоянии от графика функции. Поэтому касательная проходит касательно графика функции под определённым углом и не могут проходить через точку касания несколько касательных под разными углами. Уравнения касательной и уравнения нормали к графику функции составляются с помощью производной.
Уравнение касательной выводится из уравнения прямой.
Выведем уравнение касательной, а затем — уравнение нормали к графику функции.
В нём k — угловой коэффициент.
Отсюда получаем следующую запись:
Значение производной f ‘(x 0 ) функции y = f(x) в точке x 0 равно угловому коэффициенту k = tgφ касательной к графику функции, проведённой через точку M 0 (x 0 , y 0 ) , где y 0 = f(x 0 ) . В этом состоит геометрический смысл производной.
Таким образом, можем заменить k на f ‘(x 0 ) и получить следующее уравнение касательной к графику функции:
В задачах на составление уравнения касательной к графику функции (а мы уже скоро к ним перейдём) требуется привести получившееся по вышеприведённой формуле уравнение к уравнению прямой в общем виде. Для этого нужно все буквы и числа перенести в левую часть уравнения, а в правой части оставить ноль.
Теперь об уравнении нормали. Нормаль — это прямая, проходящая через точку касания к графику функции перпендикулярно касательной. Уравнение нормали:
Переходим к примерам. Для решений потребуется таблица производных (откроется в новом окне).
Для разминки первый же пример прелагается решить самостоятельно, а затем посмотреть решение. Есть все основания надеяться, что для наших читателей эта задача не будет «холодным душем».
Пример 0. Составить уравнение касательной и уравнение нормали к графику функции 
Решаем задачи вместе
Пример 1. Составить уравнение касательной и уравнение нормали к графику функции 

Решение. Найдём ординату точки касания:

Найдём производную функции (функция представляет собой многочлен и её производную можно найти по формулам 1, 2 и 3 в таблице производных):

Найдём значение производной в точке касания, то есть угловой коэффициент касательной:

Теперь у нас есть всё, что требуется подставить в приведённую в теоретической справке запись, чтобы получить уравнение касательной. Получаем
В этом примере нам повезло: угловой коэффициент оказался равным нулю, поэтому отдельно приводить уравнение к общему виду не понадобилось. Теперь можем составить и уравнение нормали:
На рисунке ниже: график функции бордового цвета, касательная зелёного цвета, нормаль оранжевого цвета.
Следующий пример — тоже не сложный: функция, как и в предыдущем, также представляет собой многочлен, но угловой коэффициен не будет равен нулю, поэтому добавится ещё один шаг — приведение уравнения к общему виду.
Пример 2. Составить уравнение касательной и уравнение нормали к графику функции 

Решение. Найдём ординату точки касания:

Найдём производную функции:

Найдём значение производной в точке касания, то есть угловой коэффициент касательной:

Подставляем все полученные данные в «формулу-болванку» и получаем уравнение касательной:
Приводим уравнение к общему виду (все буквы и числа, отличные от нуля, собираем в левой части, а в правой оставляем ноль):
Составляем уравнение нормали:
Пример 3. Составить уравнение касательной и уравнение нормали к графику функции 

Решение. Найдём ординату точки касания:


Найдём значение производной в точке касания, то есть угловой коэффициент касательной:

Находим уравнение касательной:
Перед тем, как привести уравнение к общему виду, нужно его немного «причесать»: умножить почленно на 4. Делаем это и приводим уравнение к общему виду:
Составляем уравнение нормали:
Решить задачи самостоятельно, а затем посмотреть решения
Пример 4. Составить уравнение касательной и уравнение нормали к графику функции 

Пример 5. Составить уравнение касательной и уравнение нормали к графику функции 

Снова решаем задачи вместе
Пример 6. Составить уравнение касательной и уравнение нормали к графику функции 

Решение. Найдём ординату точки касания:


Найдём значение производной в точке касания, то есть угловой коэффициент касательной:

Получаем уравнение касательной:
Приводим уравнение к общему виду:
Составляем уравнение нормали:
Распространённая ошибка при составлении уравнений касательной и нормали — не заметить, что функция, данная в примере, — сложная и вычислять её производную как производную простой функции. Следующие примеры — уже со сложными функциями (соответствующий урок откроется в новом окне).
Пример 7. Составить уравнение касательной и уравнение нормали к графику функции 

Решение. Найдём ординату точки касания:

Внимание! Данная функция — сложная, так как аргумент тангенса ( 2x ) сам является функцией. Поэтому найдём производную функции как производную сложной функции (потребуется формула 9 в таблице производных сложной функции):

Найдём значение производной в точке касания, то есть угловой коэффициент касательной:

Получаем уравнение касательной:
Приводим уравнение к общему виду:
Составляем уравнение нормали:
Пример 8. Составить уравнение касательной и уравнение нормали к графику функции 

Решение. Найдём ординату точки касания:

Как и в предыдущем примере, данная функция — сложная, так как степень (

Найдём значение производной в точке касания, то есть угловой коэффициент касательной:

Уравнение касательной и нормали к неявной кривой
ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ
Пусть имеем функцию y=f(x), где x – независимая переменная. Тогда дифференциал этой функции dy=f‘(x)dx также зависит от переменной x, причем от x зависит только первый сомножитель f‘(x) , а dx = Δx от x не зависит (приращение в данной точке x можно выбирать независимо от этой точки). Рассматривая dy как функцию x, мы можем найти дифференциал этой функции.
Дифференциал от дифференциала данной функции y=f(x) называется вторым дифференциалом или дифференциалом второго порядка этой функции и обозначается d 2 y: d(dy)=d 2 y.
Найдем выражение второго дифференциала. Т.к. dx от x не зависит, то при нахождении производной его можно считать постоянным, поэтому
Аналогично третьим дифференциалом или дифференциалом третьего порядка функции называется дифференциал от ее второго дифференциала:
Вообще дифференциалом n-го порядка называется первый дифференциал от дифференциала (n – 1)-го порядка: d n (y)=d(d n-1 y)
| d n y = f (n) (x)dx n |
Отсюда, пользуясь дифференциалами различных порядков, производную любого порядка можно представить как отношение дифференциалов соответствующего порядка:
ПРОИЗВОДНАЯ НЕЯВНОЙ ФУНКЦИИ
Пусть значения двух переменных x и y связаны между собой некоторым уравнением, которое символически запишем так:
| F(x, y) = 0. | (1) |
Если на некотором множестве D каждому значению переменной x соответствует единственное значение y, которое вместе с x удовлетворяет уравнению (1), то будем говорить, что это уравнение задает неявную функцию y=f(x).
Из определения следует, что для любой неявной функции y=f(x), заданной уравнением (1), имеет место тождество F(x, f(x)) ≡ 0, справедливое при всех x Î D.
Например, уравнение x 2 + y 2 – a 2 = 0 неявно определяет две элементарные функции 
Однако, не всякую неявно заданную функцию можно представить явно, т.е. в виде y=f(x).
Например, функции, заданные уравнениями y 2 – y – x 2 =0 или 
Заметим, что каждая явная функция y=f(x) может быть представлена и как неявная y–f(x) = 0.
Таким образом, неявная функция – это определенный способ задания зависимости между переменными x и y.
Рассмотрим правило нахождения производной неявной функции, не преобразовывая ее в явную, т.е. не представляя в виде y=f(x).
Чтобы найти производную у‘ неявной функции F(x, y)=0, нужно обе части этого уравнения продифференцировать по x, рассматривая у как функцию от x, и из этого полученного уравнения найти искомую производную y‘. Чтобы найти y», нужно уравнение F(x, y)=0 дважды продифференцировать по x и выразить y» и т.д.
Примеры. Найти производные функций заданных неявно.
Итак, производная неявной функции выражается, как правило, не только через аргумент, но и через функцию.
ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИЙ, ЗАДАННЫХ ПАРАМЕТРИЧЕСКИ
Пусть даны два уравнения
| x=x(t),y=y(t), где t Î [T1, T2]. | (1) |
Каждому значению t из [T1, T2] соответствуют определенные значения x и y. Если рассматривать значения x и y как координаты точки на плоскости xOy, то каждому значению t будет соответствовать определенная точка плоскости. Когда t изменяется от T1 до T2, эта точка на плоскости описывает некоторую кривую. Уравнения (1) называются параметрическими уравнениями этой кривой, t называется параметром, а способ задания кривой уравнениями (1) называется параметрическим.
Предположим, что функция x=x(t) имеет обратную t=t(x). Тогда, очевидно, у является функцией от x: y=y[t(x)]. Следовательно, уравнения (1) определяют y как функцию от x, и говорят, что функция y от x задается параметрически.
При рассмотрении функций, заданных параметрически, исключение параметра не всегда возможно. Во многих случаях удобнее задавать различные значения t и затем вычислять соответствующие значения аргумента x и функции y.
Пример. Пусть кривая задана параметрическими уравнениями:
Построим эту кривую на плоскости, придавая различные значения параметру t и находя соответствующие значения х и у.
При t =0 M(R, 0).
Таким образом, получаем окружность с центром в начале координат, радиуса R. Здесь t обозначает угол, образованный радиусом, проведенным в некоторую точку окружности М(x, y), и осью Ox.
Если исключим из этих уравнений параметр t, то получим уравнение окружности, содержащее только x и y. Возводя в квадрат параметрические уравнения и складывая их, находим:
Выведем правило нахождения производных функций, заданных параметрически. Пусть x=x(t), y=y(t), причем на некотором отрезке [T1, T2] функции x(t) и y(t) дифференцируемы и x‘ ≠ 0.
Т.к. у – функция, зависящая от переменной x, то будем считать, что функция x=x(t) имеет обратную t=t(x).
Будем обозначать: yx‘ – производная функции по переменной x, yt‘, xt‘, tx‘ – соответственно производные по t и х.
Воспользовавшись правилом дифференцирования сложной функции, получим 

Окончательно, 
Полученную функцию 

Используя эту формулу, можно находить и производные высших порядков функций, заданных параметрически. Найдем 

 , y = arcsin (t–1). Найдем
, y = arcsin (t–1). Найдем  .
.Следовательно, 
Найти угловой коэффициент касательной к циклоиде x = a·(t – sin t), y = a·(1 – cost)
в произвольной точке (0 ≤t≤ 2·π).
Угловой коэффициент касательной 
x‘ = a·(1 – cost) ,y‘ = a·sin t. Поэтому 
Найти 
УРАВНЕНИЯ КАСАТЕЛЬНОЙ И НОРМАЛИ К КРИВОЙ
Рассмотрим кривую, уравнение которой есть y=f(x). Возьмем на этой кривой точку M(x0, y0), и составим уравнение касательной к данной кривой в точке M, предполагая, что эта касательная не параллельна оси Oy.
Уравнение прямой с угловым коэффициентом в общем виде есть у=kx + b. Поскольку для касательной k= f‘(x0), то получаем уравнение y= f‘(x0)·x + b. Параметр b найдем из условия, что касательная проходит через точку M(x0, y0). Поэтому ее координаты должны удовлетворять уравнению касательной: y0= f‘(x0)·x0 + b. Отсюда b=y0– f‘(x0)·x0.
| y = f ‘(x0)·(x – x0) + f(x0) |
Если касательная, проходящая через точку М(x0,y0) параллельна оси ординат (т.е. производная в этой точке не существует), то ее уравнение x= x0.
Наряду с касательной к кривой в данной точке часто приходится рассматривать нормаль.
Нормалью к кривой в данной точке называется прямая, проходящая через эту точку перпендикулярно к касательной в данной точке.
Из определения нормали следует, что ее угловой коэффициент kn связан с угловым коэффициентом касательной k равенством:

Учитывая, что нормаль также как и касательная проходит через точку M(x0, y0), то уравнение нормали к кривой y= f(x) в данной точке M имеет вид:
Ясно, что если касательная параллельна оси Ox, т.е.f‘(x0) = 0 и ее уравнение имеет вид y= y0, то нормаль в этой же точке будет перпендикулярна оси Ox. Значит, ее уравнение имеет вид x= x0.
- Составить уравнения касательной и нормали к графику функции у = tg 2 x в точке с абсциссой x0=π/4.
Уравнение касательной имеет вид y =4·(x – π/4) + 1 или y = 4x – π + 1.
Уравнение нормали будет y = –1/4·(x – π/4) + 1 или у = –1/4·x + π/16 + 1.
Составить уравнения касательной и нормали к графику функции у = 0.5·(x – 2) 2 + 5 в точке M(2; 5).
y‘= x – 2, y‘(2) = 0 . Следовательно, касательная параллельна оси Ox, а значит ее уравнение y= 5 . Тогда нормаль параллельна оси Oy и имеет уравнение x= 2 .
Найти уравнение касательной и нормали к эллипсу 
Найдем y‘ по правилу дифференцирования неявной функции 
Уравнение касательной: 

Уравнение нормали: 

Составить уравнения касательной и нормали к циклоиде x= t – sin t, y= 1 – cos tв точке М(x0; y0), которая соответствует значению параметра t = π/2.

Уравнение касательной: y = x – π/2 + 1 + 1, т.е. у = x – π/2 + 2.
Уравнение нормали: y = – x – π/2 – 1 + 1, т.е. у = – x – π/2.
ТЕОРЕМЫ О ДИФФЕРЕНЦИРУЕМЫХ ФУНКЦИЯХ
Теорема Ролля. Если функция y= f(x) непрерывна на отрезке [a; b], дифференцируема во всех внутренних точках этого отрезка (т.е. на (а; b)) и на концах отрезка обращается в нуль f(a) = f(b) = 0, то на (a; b) найдется хотя бы одна точка c Î (a; b), в которой f‘(c) = 0.
Доказательство. Так как функция f(x) непрерывна на [a; b], то по одной из теорем о непрерывных функциях она достигает на этом отрезке наибольшего значения и наименьшего. Пусть
Заметим, что если М = m, то f(x) = const = 0 (по условию теоремы f(a)=f(b)=0) и, следовательно, f‘(x)=0при всех x Î [a; b] .
Предположим, что M≠m, тогда, по крайней мере, одно из этих чисел отлично от нуля. Для определенности будем считать, что М ≠0 и М > 0.
Пусть в точке x = c f(c)=М, при этом c≠a и с ≠ b, т.к. f(a)=f(b)=0. Придадим значению c приращение Δx и рассмотрим новую точку c+Δx. Поскольку f(c) – наибольшее значение функции, то f(c+Δx) – f(c)≤0 для любого Δx. Отсюда следует, что
Переходя в этих неравенствах к пределу при Δx→0 и учитывая, что производная при x = c существует, будем иметь:
Но неравенства f‘(c) ≤ 0 и f‘(c) ≥ 0 одновременно возможны лишь в случае, когда
Эта теорема имеет простой геометрический смысл. Если непрерывная кривая, имеющая в каждой точке касательную, пересекает ось Ox в точках x=a и x=b, то на этой кривой найдется хотя бы одна точка с абсциссой c, a Î (a; b), что F‘(c)=0. Но F ‘(x) = f‘(x) – k, а значит,F‘(c) = f‘(c) – k = 0.
Подставляя в это равенство значение k, получим

что и требовалось доказать.
Теорему Лагранжа геометрически можно пояснить так. Рассмотрим график функции y=f(x), удовлетворяющий условиям теоремы и соединим концы графика на [a; b] хордой AB. Как мы уже отметили, отношение 
Теорема Коши. Если f(x) и g(x) – две функции, непрерывные на [a; b] и дифференцируемые внутри него, причем g‘(x) ≠ 0 при всех x Î (a; b), то внутри отрезка [a; b] найдется хотя бы одна точка c Î (a; b), что 
Доказательство.Определим число 
Составим вспомогательную функцию.
Несложно заметить, что F(a)=F(b)=0. Функция F(x) удовлетворяет на [a;b] всем условиям теоремы Ролля. Следовательно, найдется число сÎ(a; b) такое, что F‘(c) = 0. Но
откуда
Заметим, что теорему Коши нельзя 

http://function-x.ru/derivative_and_tangent.html
http://toehelp.ru/theory/math/lecture07/lecture07.html
































