Уравнение касательной и нормали плоской кривой

Лекция Плоские кривые. Способы задания плоской кривой.Длина плоской кривой. Касательная и нормаль к кривой. Кривизна кривой. Эволюта и эвольвента

III . ПЛОСКИЕ КРИВЫЕ.

1. Способы задания плоских кривых.

2. Уравнения касательной и нормали.

3. Формулы для нахождения единичного вектора нормали и кривизны.

4. Уравнение эволюты.

3.1 СПОСОБЫ ЗАДАНИЯ ПЛОСКОЙ КРИВОЙ.

Кривая, у которой кручение в каждой точке равно нулю, располагается в плоскости и поэтому называется плоской. В качестве такой плоскости выбирают плоскость хОу.

Геометрию плоских кривых можно получить как частный случай геометрии кривых в пространстве, но при таком подходе могут ускользнуть многие своеобразные их особенности. В связи с этим теория плоских кривых строится независимо от теории кривых в пространстве.

Кривую на плоскости можно задать уравнениями различных видов, наиболее распространенными из которых являются:

а) векторное уравнение , (3.1)

б) векторно-параметрическое уравнение (3.2)

в) координатно-параметрические уравнения

г) уравнение в несимметричной форме

или (3.5)

Заметим, что присоединив к уравнению (3.4) тождество х=х , получим параметрические уравнения х=х, y = f ( x ). Они отличаются от уравнений (3.3) тем, что за параметр принята абсцисса точка кривой.

В частности, если какая-либо точка кривой не является особой (т.е. отлична от нуля по крайней мере одна из производных в этой точке), то в ее окрестности уравнение (3.6) можно разрешить или относительно у (при ), и тогда получим уравнение (3.4), или относительно х (при ), тогда получим уравнение (3.5).

3.2 ДЛИНА ПЛОСКОЙ КРИВОЙ.

Длиной кривой называется верхняя грань всех возможных ломаных, вписанных в данную кривую. В частности, если кривая задана векторно-параметрическим уравнением и функция непрерывна вместе со своей производной на , то она спрямляема.

а) Длина кривой в прямоугольных координатах .

Если плоская кривая задана уравнением , где функция непрерывна вместе со своей производной на [ a , b ], то она спрямляема и ее длина выражается формулой

(3.7)

Если кривая задана параметрическими уравнениями и функции непрерывно дифференцируемы на [ T ₁ , T ₂ ], то ее длина выражается формулой:

(3.8)

б) Длина кривой в полярных координатах.

Если кривая задана в полярных координатах уравнением и функция непрерывна вместе со своей производной на , то ее длина выражается формулой

(3.9)

Пример 3.1 Найти длину полукубической параболы ay 2 = x 3 , a >0 от х =0 до х=5а .

Решение: Из уравнений кривой следует, что полукубическая парабола симметрична относительно оси абсцисс (замена у= ‑у не изменяет уравнения) и расположена в правой полуплоскости координатной полуплоскости хОу ( х не может быть отрицательным). Вычислим длину одной ветви кривой ОА.

Из уравнения кривой находим .

По формуле (3.7) получим:

.

Длина кривой равна S =670 а /27.

Пример 3.2 Вычислить длину кардиоиды .

Решение: Однозначная ветвь функции r соответствует изменению параметра в промежутке , при этом кривая симметрична относительно полярной оси. При изменении от 0 до полярный радиус r опишет половину кривой. Половину длины кардиоиды найдем, используя формулу (3.9):

Длина всей кардиоиды S =8 a .

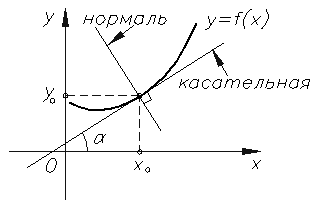
3.3 КАСАТЕЛЬНАЯ И НОРМАЛЬ К КРИВОЙ.

Единичный вектор направленной касательной, как мы показали выше (1.7), находится как орт производной радиус-вектора: .

На практике иногда удобнее в качестве направляющего вектора касательной брать вектор (или любой ему коллинеарный вектор) и уравнение касательной в точке записать в виде:

(3.10)

или . (3.11)

В качестве направляющего вектора нормали можно взять единичный вектор главной нормали , или, что на практике гораздо проще, вектор , ортогональный вектору , тогда уравнение нормали будет иметь вид:

(3.12)

или . (3.13)

Если кривая задана уравнением в несимметричной форме (3.4), то касательная и нормаль соответственно имеют уравнения

(3.14)

(3.15)

г) Если кривая задана уравнением в симметричной форме (3.6), то касательная и нормаль соответственно имеют уравнения

(3.16)

(3.17)

Пример 3.3 Составить уравнение касательной и нормали к кривой y = x 3 -2 в точке А(2,3).

Решение: Используем уравнение касательной (3.14) и нормали для кривой, заданной в несимметричной форме. Запишем уравнение пучка прямых, проходящих через данную точку А(2,3): y -3= k ( x -2),

где k – угловой коэффициент прямой (в данном случае произвольный параметр). Для определения k , соответствующего касательной и нормали к кривой, найдем производную при х =2:

Следовательно, для касательной k =12, для нормали k = ‑ 1/12. Подставляя эти значения в уравнение пучка прямых, получим уравнение касательной

.

Пример 3.4 Составить уравнение касательной и нормали к декартовому листу х 3 +у 3 -3аху=0, а>0 (рис.9) в точке А ( 3а/2;3а/2 ).

Решение. Используем уравнения касательной (3.16) и нормали (3.17) для кривой заданной в симметричной форме. Записав исходное уравнение в виде F( x,y )=0 , найдем:

Подставляя значения производных в уравнение касательной

и нормали: ,

получим уравнение касательной у=3а-х , и уравнение нормали у=х .

3.4 КРИВИЗНА КРИВОЙ. ЭВОЛЮТА И ЭВОЛЬВЕНТА КРИВОЙ.

Если кривая задана уравнением у=у(х), то ее кривизна определяется по формуле:

(3.18)

В случае векторно-параметрического задания кривой

(3.19)

Радиус кривизны в данной точке:

(3.20)

Всякая прямая, проходящая через точку кривой и перпендикулярная касательной в этой точке, называется нормалью к кривой в данной точке. Вектор нормали к кривой, направленный в сторону центра кривизны и указывающий направление, в котором кривая в окрестности рассматриваемой точки отклоняется от своей касательной, называется вектором главной нормали. Множество центров кривизны кривой образуют ее эволюту. В случае векторно-параметрического задания кривой уравнение эволюты имеет вид (2.17): , и координаты центра кривизны определяются формулами:

, (3.21)

Если кривая задана уравнением y = f ( x ) , то

, (3.22)

Исходная кривая по отношению к своей эволюте называется эвольвентой.

Пример 3.5 Найти кривизну и радиус кривизны параболы у=х 2 в произвольной точке х.

Решение: Кривизну параболы найдем, подставляя в (3.18):

Эта величина принимает наибольшее значение при х =0, для которого k =2. Радиус кривизны связан с кривизной соотношением (3.20), поэтому

Наименьший радиус кривизны в точке (0,0).

Пример 3.6 Найти радиус кривизны и эволюту эллипса .

Решение: Представим уравнение эллипса в параметрическом виде:

Подставляя в формулы (3.19) и (3.20), получим

.

Уравнение эволюты найдем по формуле (3.21):

Таким образом, эволютой эллипса является астроида.

Геометрическое применение производной: уравнения касательной и нормали, угол между кривыми

Касательная и нормаль к кривой

Касательная прямая — прямая, проходящая через точку кривой и совпадающая с ней в этой точке с точностью до первого порядка.

Прямая, проходящая через точку касания, перпендикулярно касательной, называется нормалью к кривой.

Если кривая определена уравнением $y=f(x)$, то уравнение касательной к ней в точке $M(x_0;y_0)$ имеет вид:

а уравнение нормали:

Задание. Написать уравнение касательной и нормали к кривой $y=x^2-3x+4$ в точке с абсциссой $x_0=0$.

Решение. Находим значение функции в заданной точке:

Далее вычислим значение производной функции в точке $x_0=0$:

а тогда уравнение касательной запишется в виде:

или после упрощения:

$$y-4=-\frac<1><-3>(x-0) \Rightarrow x-3 y+12=0$$

Ответ. Уравнение касательной: $3x+y-4=0$

Уравнение нормали: $x-3y+12=0$

Угол между кривыми

Углом между кривыми на плоскости в их общей точке $M(x_0;y_0)$ называется наименьший из двух возможных углов между касательными к этим кривым в данной точке. Если уравнения касательных, проведенных к кривым $y=f_1(x)$ и $y=f_2(x)$, соответственно $y=k_<1>x+b_<1>$ и $y=k_<2>x+b_2$, то тангенс угла между кривыми определяется соотношением:

Задание. Найти тангенс угла между кривыми $y=x^2-1$ и $y=x^3-1$ в точке их пересечения, которая имеет большую абсциссу.

Решение. Вначале найдем точки пересечения графиков заданных функций, для этого совместно разрешим уравнение заданных кривых:

Таким образом, искомая точка $x=1$.

Далее находим производные заданных функций в найденной точке:

Итак, искомый тангенс:

Ответ. $\operatorname \phi=\frac<1><7>$

Геометрическое применение производной

Вы будете перенаправлены на Автор24

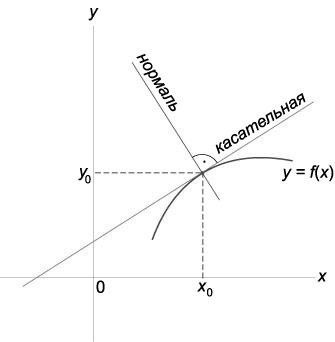
Что такое касательная и нормаль к кривой

Касательная — прямая которая совпадает и проходит через точку кривой с точностью до первого порядка.

Нормаль к кривой — прямая перпендикулярно проходящая через точку касания.

Рисунок 1. Нормаль и касательная к кривой

Для кривой вида y = f(x) уравнение касательной в точке М(x0,y0):

Для кривой вида y = f(x) уравнение касательной в точке М(x0,y0):

Написать уравнение касательной и нормали к кривой в точке с абсциссой $x_0=1$:

1. Найдем значение функции в точке: \[y_ <0>=3\cdot 1^ <2>-2\cdot 1+11=12\]
2. Найдем производную в данной точке: \[y'(x_ <0>)=\left(3x^ <2>-2x+11\right) <<'>> =6x-2\] \[y'(1)=6\cdot 1-2=4\]
3. Запишем уравнение касательной: \[y-y_ <0>=y`(x_ <0>)(x-x_ <0>)\] \[y-12=4(x-1)\] \[y-4x-8=0\]
4. Запишем уравнение нормали: \[y-12=-\frac<1><4>(x-1)\] \[4y+x-49=0\]

Угол между двумя кривыми в точке М(x0,y0) является наименьшим из возможных углов между касательными. Пусть уравнения касательных имеют вид:

Тогда тангенс угла между двумя кривыми находится по формуле:

Найти тангенс угла между кривыми, в точке имеющей большую абсциссу.

Для того чтобы определить точки пересечения кривых необходимо решить систему уравнений: \[\left\<\begin-3> \\ \end\right. \] \[2x^ <2>-3=4x-2\] \[2x^ <2>-4x=1\] \[2x(x-2)=1\]

Значит, кривые пересекаются в точках 0,5 и 2. Максимальной, из которых, является точка x = 2.

Готовые работы на аналогичную тему

Что такое длина касательной и нормали, подкасательная и поднормаль

Длина отрезка от пересечения касательной оси ОХ до пересечения с нормалью или кривой называется длиной касательной.

Проекция отрезка от пересечения касательной оси ОХ до пересечения с нормалью или кривой на ось Ох называется подкасательной (ST).

Длина отрезка от пересечения нормали с касательной или кривой до точки соприкосновения с осью Ох называется длиной нормали, а проекция отрезка на ось — поднормалью (SN).

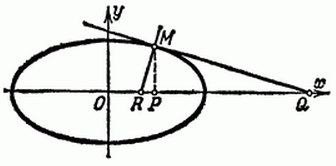
Найти длину подкасательной и поднормали для эллипса x = acost, y = bsint

Рисунок 2. Эллипс

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 15 12 2021