Касательная к кривой второго порядка
| Коэффициенты общей кривой второго порядка |
| Точка на кривой, через которую надо провести касательную |
| Заданная формула кривой второго порядка |
| Уравнение касательной в указанной точке |
Касательная к кривой
После того, как мы можем рассчитывать по произвольным координатам ту или иную кривую второго порядка на плоскости по точкам, возникла возможность рассчитать касательную в данной точке этой прямой.
Что же такое касательная? Касательная — это такая прямая которая перескает линию вида
в двух совпадающих точках ( либо целиком входит в состав этой линии)
Выше приведенная формула — есть уравнение кривой второго порядка, а значит при различных заданных коэффициентах, мы можем с помощью этого бота рассчитать уравнение касательной для:
В дальнейшем мы рассмотрим примеры, и Вы сами сможете проверить правильность вычислений.
Уравнение касательной в общем виде выглядит так:
Таким образом, зная все коэффициенты, мы очень легко найдем уравнение касательной в произвольной точке.
Синтаксис
kp2p коэффиценты;координата точки
Где коэффициенты кривой , разделенные как минимум одним пробелом, а координата точки это точка на кривой к которой и надо провести касательную.
Примеры
Вычислить уравнение касательной в точке (3:1) к окружности выраженной формулой
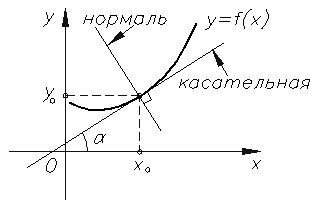
Геометрическое применение производной: уравнения касательной и нормали, угол между кривыми
Касательная и нормаль к кривой
Касательная прямая — прямая, проходящая через точку кривой и совпадающая с ней в этой точке с точностью до первого порядка.
Прямая, проходящая через точку касания, перпендикулярно касательной, называется нормалью к кривой.
Если кривая определена уравнением $y=f(x)$, то уравнение касательной к ней в точке $M(x_0;y_0)$ имеет вид:
а уравнение нормали:
Задание. Написать уравнение касательной и нормали к кривой $y=x^2-3x+4$ в точке с абсциссой $x_0=0$.
Решение. Находим значение функции в заданной точке:
Далее вычислим значение производной функции в точке $x_0=0$:
а тогда уравнение касательной запишется в виде:
или после упрощения:
$$y-4=-\frac<1><-3>(x-0) \Rightarrow x-3 y+12=0$$
Ответ. Уравнение касательной: $3x+y-4=0$
Уравнение нормали: $x-3y+12=0$
Угол между кривыми
Углом между кривыми на плоскости в их общей точке $M(x_0;y_0)$ называется наименьший из двух возможных углов между касательными к этим кривым в данной точке. Если уравнения касательных, проведенных к кривым $y=f_1(x)$ и $y=f_2(x)$, соответственно $y=k_<1>x+b_<1>$ и $y=k_<2>x+b_2$, то тангенс угла между кривыми определяется соотношением:
Задание. Найти тангенс угла между кривыми $y=x^2-1$ и $y=x^3-1$ в точке их пересечения, которая имеет большую абсциссу.
Решение. Вначале найдем точки пересечения графиков заданных функций, для этого совместно разрешим уравнение заданных кривых:
Таким образом, искомая точка $x=1$.
Далее находим производные заданных функций в найденной точке:
Итак, искомый тангенс:
Ответ. $\operatorname
Геометрическое применение производной
Вы будете перенаправлены на Автор24
Что такое касательная и нормаль к кривой
Касательная — прямая которая совпадает и проходит через точку кривой с точностью до первого порядка.
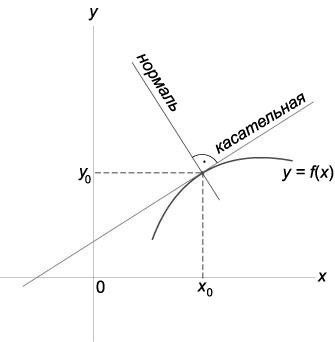
Нормаль к кривой — прямая перпендикулярно проходящая через точку касания.
Рисунок 1. Нормаль и касательная к кривой
Для кривой вида y = f(x) уравнение касательной в точке М(x0,y0):
Для кривой вида y = f(x) уравнение касательной в точке М(x0,y0):
Написать уравнение касательной и нормали к кривой в точке с абсциссой $x_0=1$:
- Найдем значение функции в точке: \[y_ <0>=3\cdot 1^ <2>-2\cdot 1+11=12\]
- Найдем производную в данной точке: \[y'(x_ <0>)=\left(3x^ <2>-2x+11\right) <<'>> =6x-2\] \[y'(1)=6\cdot 1-2=4\]
- Запишем уравнение касательной: \[y-y_ <0>=y`(x_ <0>)(x-x_ <0>)\] \[y-12=4(x-1)\] \[y-4x-8=0\]
- Запишем уравнение нормали: \[y-12=-\frac<1><4>(x-1)\] \[4y+x-49=0\]
Угол между двумя кривыми в точке М(x0,y0) является наименьшим из возможных углов между касательными. Пусть уравнения касательных имеют вид:
Тогда тангенс угла между двумя кривыми находится по формуле:
Найти тангенс угла между кривыми, в точке имеющей большую абсциссу.
- Для того чтобы определить точки пересечения кривых необходимо решить систему уравнений: \[\left\<\begin
Значит, кривые пересекаются в точках 0,5 и 2. Максимальной, из которых, является точка x = 2.
Готовые работы на аналогичную тему
Что такое длина касательной и нормали, подкасательная и поднормаль
Длина отрезка от пересечения касательной оси ОХ до пересечения с нормалью или кривой называется длиной касательной.
Проекция отрезка от пересечения касательной оси ОХ до пересечения с нормалью или кривой на ось Ох называется подкасательной (ST).
Длина отрезка от пересечения нормали с касательной или кривой до точки соприкосновения с осью Ох называется длиной нормали, а проекция отрезка на ось — поднормалью (SN).
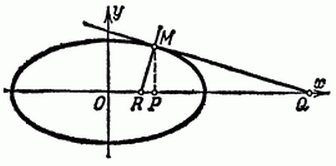
Найти длину подкасательной и поднормали для эллипса x = acost, y = bsint
Рисунок 2. Эллипс
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 15 12 2021
http://www.webmath.ru/poleznoe/formules_8_10.php
http://spravochnick.ru/matematika/proizvodnaya_i_differencial/geometricheskoe_primenenie_proizvodnoy/