Уравнение касательной к графику неявной функции

Касательная к графику функции, как составить уравнение, свойства, угловой коэффициент касательной проведенной к графику функции, формула, примеры решения

На экзаменах по дисциплинам с физико-математическим уклоном или при расчетах встречается тип задач о касательной к графику функции.

Однако следует разобраться в основных терминах и соотношениях.

Специалисты рекомендуют пользоваться специальным алгоритмом, позволяющим правильно находить точку касания прямой с какой-либо фигурой.

Общие сведения
- Определения и понятия
- Геометрический смысл
Касательные к фигурам и графикам
- Одна и несколько окружностей
- Эллипс, гипербола и парабола
Примеры решения
- Рекомендации специалистов
- Упражнения и ход вычислений

Общие сведения

Касательной называется прямая, имеющая с фигурой или графиком заданной функции одну общую точку. Однако иногда она проходит через 2 точки. В этом случае ее называют секущей. Прямая задается следующим уравнением: y = kx + b. Значение «k» — это угловой коэффициент.

Для решения задач следует разобрать основные понятия, определения, формулы и свойства касательной.

Кроме того, очень важно понять ее геометрический смысл, поскольку без него будет сложно разобраться в более сложных дисциплинах с физико-математическим уклоном.

Определения и понятия

У касательной есть определенный параметр — угол наклона (а).

Его необходимо отсчитывать от оси абсцисс (только положительное направление) к прямой, заданной графиком y = kx + b.

От него зависит ее расположение.

Коэффициент «к» равен значению тангенса угла наклона, т. е. tg(a).

Математики сделали некоторые выводы, которые основываются на значении углового коэффициента:

В первом, втором и третьем случаях коэффициент является положительным, а в последнем — отрицательным. Эти факты следует учитывать при решении задач. Касательная прямая может являться и секущей, т. е. соприкасаться с графиком функции сразу в двух и более точках. Следует отметить, что при параллельности прямой оси ОХ (y = b), она может пересекать функцию бесконечное число раз.

Существует еще одно определение: касательной к функции вида y = f(x) в точке (х0, f(x0)) является прямая, которая проходит через эту точку с тем условием, что отрезок имеет множество значений, близких к ней (х -> x0).

Геометрический смысл

Пусть дана некоторая функция y = f(x) и секущая АВ (рис. 1). Координаты последней в точках А и В следующие: А(х0;f(x0)) и В(х0+zx;f(x0+zx)). Величина «zx» — приращение аргумента по х, которое показано стрелками. Если подставить координаты в функцию, то она имеет такой вид: zy = zf(x) = f(x0+zx) — f(zx).

Рисунок 1. Геометрический смысл.

Соотношение, которое было получено выше, называется производной. Если к графику в точке проведена секущая или касательная, то тангенс угла будет равен самой производной заданной функции в точке с координатой х0.

Из этого определения можно сделать вывод о существовании производной. Если значение последней равно 0, то, следовательно, не существует общих точек с заданной фигурой.

Касательные к фигурам и графикам

При решении задач следует обратить внимание на частные случаи. Нужно произвести расчеты уравнения прямой или найти точки соприкосновения с окружностью, эллипсом, гиперболой или параболой. Очень распространенная задача встречается также в механике о ременной передаче.

Частные случаи позволят найти оптимальное решение и метод расчета, поскольку экономия времени является важным элементом при научных исследованиях, написании контрольных работ и сдаче экзаменов. Важный этап — идентификация типа задачи. Касательная к вышеперечисленным фигурам — основной тип заданий, но существуют и более сложные функции.

Например, сложно составить уравнение прямой, которая имеет точки касания с какой-либо сложной функцией.

В некоторых случаях необходимо перед выполнением расчетов ее упростить, т. е. привести подобные слагаемые, раскрыть скобки или воспользоваться другими приемами для упрощения выражения.

Одна и несколько окружностей

Радиус, который проводится через точку касания, составляет с касательной прямой угол (перпендикулярен). Перпендикуляр к касательной, проходящий через точку касания, является радиусом или диаметром заданного круга. Из этого следует, что радиус является нормалью по отношению к прямой. Секущая — прямая, которая проходит через график или фигуру, но имеет от двух и более точек пересечения.

Формула окружности с центром в точке О (xc;yc) и радиусом R имеет следующий вид: sqr(х-хc) + sqr(y-yc) = R^2.

Для решения следует выразить значение у, но при этом нужно рассматривать 2 случая:

y = sqrt[R^2 — (х-хc)^2] + yц.

y = -sqrt[R^2 — (х-хc)^2] + yц.

Две функции являются полукругами и вместе образуют окружность. Чтобы составить график круга в точке (х0;у0), нужно уравнение в этой точке. В точках с координатами (хц;yц+R) и (хц;yц-R) уравнения касательных к окружности задаются следующими уравнениями: y = yц + R и y = yц — R. Если взять точки (хц+R;yц) и (хц-R;yц), они будут иметь такую форму: x = xц + R и x = xц — R.

В случае для двух окружностей всего можно провести до 4 касательных (2 внешних и 2 внутренних). Это зависит от случая расположения фигур. Точкой пересечения внешних считается внешняя гомотетия (подобие), а внутренних — в центре внутреннего подобия. Внешними называются прямые, которые касаются внешних точек круга. Если касательные являются внутренними, то они пересекают линию, соединяющую центры окружностей.

Следует отметить, что внешний и внутренний центры гомотетии лежат на некоторой прямой. Она проходит через центры заданных окружностей. Это был рассмотрен случай, когда одна окружность меньше другой.

Однако при равенстве их диаметров появляются некоторые свойства: внешние касательные параллельны и внешнего центра гомотетии не существует.

Основные соотношения можно вывести, используя уравнение прямой (касательной) и расстояние от точки до прямой. Пусть окружности с радиусами R1 и R2 имеют следующие координаты центров: с1(х1;у1) и с2(х2;у2). Уравнение прямой записывается таким образом: ах + by + c = 0. Расстояния до прямой от точек с1 и с2 вычисляются таким образом: ах1 + by1 + c = R1 и ах2 + by2 + c = R2. Формула находится с помощью вычитания первого уравнения из второго: а(х2 — х1) + b(y2 — у1) = R2 — R1. Следовательно, расстояние вычисляется по следующей формуле: d = sqrt[(х2 — х1)^2 + (y2 — у1)^2].

Эллипс, гипербола и парабола

Пусть задан эллипс с полуосями a и b.

Его центром является точка с координатами (xц;уц). Уравнение, описывающее фигуру имеет такой вид: [(х — хц)^2 / a^2] + [(y — yц)^2 / b^2] = 1. Необходимо выразить переменную y. Функция будет состоять из двух полуэллипсов: y = (b/a) * sqrt[a^2 — (x-xц)^2] + yц и y = -(b/a) * sqrt[a^2 — (x-xц)^2] + yц. Касательные к геометрической фигуре могут быть параллельными оси ОХ или ОУ.

В некоторых случаях график задан уравнениями кривых, к которым относятся гипербола и парабола. Пусть первая имеет координаты центра (xц;уц) с вершинами (xц+а;уц) и (xц-a;уц). Ее уравнение принимает такой вид: [(х — хц)^2 / a^2] — [(y — yц)^2 / b^2] = 1. Если же ее вершины имеют такие координаты (xц;уц+b) и (xц;уц-b), то она описывается следующим равенством [(х — хц)^2 / a^2] — [(y — yц)^2 / b^2] = -1. В последнем равенстве меняется знак. При решении нужно разбить на две объединенные функции:

y = (b/a) * sqrt[(x-xц)^2 — a^2] + yц и y = -(b/a) * sqrt[(x-xц)^2 — a^2] + yц.

y = (b/a) * sqrt[(x-xц)^2 + a^2] + yц и y = -(b/a) * sqrt[(x-xц)^2 + a^2] + yц.

В первом случае прямые параллельны оси ординат, а во втором — абсцисс. Чтобы написать уравнение прямой, нужно определить, к какой из функций принадлежит точка, выполнив подстановку в текущие равенства. После этого их следует проверить на тождественность.

Чтобы записать уравнение прямой-касательной к параболе y = ax^2 + bx + c в точке с координатами (x0;y(x0)), нужно привести равенство к следующему виду: y = y'(x0) * (x-x0) + y(x0). Из формулы можно сделать вывод о том, что прямая параллельна оси абсцисс. Параболу нужно рассматривать, как объединение двух функций (x = ay^2 + by + c). Рекомендуется решить его относительно y. Дискриминант вычисляется таким образом: D = b^2 — 4a(c — x).

В зависимости от его значения находятся корни:

D>0: y = [-b + sqrt(D)] / 2a и y = [-b — sqrt(D)] / 2a.

D=0: y = -b / 2a.

Учитель физики, информатики и вычислительной техники. Победитель конкурса лучших учителей Российской Федерации в рамках Приоритетного Национального Проекта «Образование».

Уравнение касательной и уравнение нормали к графику функции

Как получить уравнение касательной и уравнение нормали

Касательная — это прямая, которая касается графика функции в одной точке и все точки которой находятся на наименьшем расстоянии от графика функции. Поэтому касательная проходит касательно графика функции под определённым углом и не могут проходить через точку касания несколько касательных под разными углами. Уравнения касательной и уравнения нормали к графику функции составляются с помощью производной.

Уравнение касательной выводится из уравнения прямой.

Выведем уравнение касательной, а затем — уравнение нормали к графику функции.

В нём k — угловой коэффициент.

Отсюда получаем следующую запись:

Значение производной f ‘(x 0 ) функции y = f(x) в точке x 0 равно угловому коэффициенту k = tgφ касательной к графику функции, проведённой через точку M 0 (x 0 , y 0 ) , где y 0 = f(x 0 ) . В этом состоит геометрический смысл производной.

Таким образом, можем заменить k на f ‘(x 0 ) и получить следующее уравнение касательной к графику функции:

В задачах на составление уравнения касательной к графику функции (а мы уже скоро к ним перейдём) требуется привести получившееся по вышеприведённой формуле уравнение к уравнению прямой в общем виде. Для этого нужно все буквы и числа перенести в левую часть уравнения, а в правой части оставить ноль.

Теперь об уравнении нормали. Нормаль — это прямая, проходящая через точку касания к графику функции перпендикулярно касательной. Уравнение нормали:

Переходим к примерам. Для решений потребуется таблица производных (откроется в новом окне).

Для разминки первый же пример прелагается решить самостоятельно, а затем посмотреть решение. Есть все основания надеяться, что для наших читателей эта задача не будет «холодным душем».

Пример 0. Составить уравнение касательной и уравнение нормали к графику функции в точке M (1, 1) .

Решаем задачи вместе

Пример 1. Составить уравнение касательной и уравнение нормали к графику функции , если абсцисса точки касания .

Решение. Найдём ординату точки касания:

Найдём производную функции (функция представляет собой многочлен и её производную можно найти по формулам 1, 2 и 3 в таблице производных):

Найдём значение производной в точке касания, то есть угловой коэффициент касательной:

Теперь у нас есть всё, что требуется подставить в приведённую в теоретической справке запись, чтобы получить уравнение касательной. Получаем

В этом примере нам повезло: угловой коэффициент оказался равным нулю, поэтому отдельно приводить уравнение к общему виду не понадобилось. Теперь можем составить и уравнение нормали:

На рисунке ниже: график функции бордового цвета, касательная зелёного цвета, нормаль оранжевого цвета.

Следующий пример — тоже не сложный: функция, как и в предыдущем, также представляет собой многочлен, но угловой коэффициен не будет равен нулю, поэтому добавится ещё один шаг — приведение уравнения к общему виду.

Пример 2. Составить уравнение касательной и уравнение нормали к графику функции , если абсцисса точки касания .

Решение. Найдём ординату точки касания:

Найдём производную функции:

Найдём значение производной в точке касания, то есть угловой коэффициент касательной:

Подставляем все полученные данные в «формулу-болванку» и получаем уравнение касательной:

Приводим уравнение к общему виду (все буквы и числа, отличные от нуля, собираем в левой части, а в правой оставляем ноль):

Составляем уравнение нормали:

Пример 3. Составить уравнение касательной и уравнение нормали к графику функции , если абсцисса точки касания .

Решение. Найдём ординату точки касания:

Найдём значение производной в точке касания, то есть угловой коэффициент касательной:

Находим уравнение касательной:

Перед тем, как привести уравнение к общему виду, нужно его немного «причесать»: умножить почленно на 4. Делаем это и приводим уравнение к общему виду:

Составляем уравнение нормали:

Решить задачи самостоятельно, а затем посмотреть решения

Пример 4. Составить уравнение касательной и уравнение нормали к графику функции , если абсцисса точки касания .

Пример 5. Составить уравнение касательной и уравнение нормали к графику функции , если абсцисса точки касания .

Снова решаем задачи вместе

Пример 6. Составить уравнение касательной и уравнение нормали к графику функции , если абсцисса точки касания .

Решение. Найдём ординату точки касания:

Найдём значение производной в точке касания, то есть угловой коэффициент касательной:

Получаем уравнение касательной:

Приводим уравнение к общему виду:

Составляем уравнение нормали:

Распространённая ошибка при составлении уравнений касательной и нормали — не заметить, что функция, данная в примере, — сложная и вычислять её производную как производную простой функции. Следующие примеры — уже со сложными функциями (соответствующий урок откроется в новом окне).

Пример 7. Составить уравнение касательной и уравнение нормали к графику функции , если абсцисса точки касания .

Решение. Найдём ординату точки касания:

Внимание! Данная функция — сложная, так как аргумент тангенса ( 2x ) сам является функцией. Поэтому найдём производную функции как производную сложной функции (потребуется формула 9 в таблице производных сложной функции):

Найдём значение производной в точке касания, то есть угловой коэффициент касательной:

Получаем уравнение касательной:

Приводим уравнение к общему виду:

Составляем уравнение нормали:

Пример 8. Составить уравнение касательной и уравнение нормали к графику функции , если абсцисса точки касания .

Решение. Найдём ординату точки касания:

Как и в предыдущем примере, данная функция — сложная, так как степень () сама является функцией. Поэтому найдём производную функции как производную сложной функции (используя формулу 1 в таблице производных сложной функции):

Найдём значение производной в точке касания, то есть угловой коэффициент касательной:

Касательная и нормаль к графику функции

Основные формулы

Пусть на некотором интервале X задана функция . Нас интересуют геометрические характеристики графика этой функции в некоторой заданной точке при значении аргумента , где . Пусть функция имеет в производную, которую будем обозначать как . Тогда через точку мы можем провести касательную к графику. Тангенс угла α между осью абсцисс x и касательной равен производной функции в точке :
(1) .
А само уравнение касательной имеет вид:
(2) .
В аналитической геометрии тангенс угла между прямой и осью абсцисс называют угловым коэффициентом прямой. Таким образом производная равна угловому коэффициенту касательной в .
См. Геометрический смысл производной

Прямая, перпендикулярная касательной, проведенной через точку , называется нормалью к графику функции в этой точке. Уравнение нормали имеет вид:
(3) .
См. Уравнение прямой с угловым коэффициентом ⇓

Пусть две кривые и пересекаются в точке . Тогда угол φ между касательными к этим кривым в точке называется углом между кривыми. Он определяется по формуле:
(4) , где .
Отсюда .
при .
Вывод формулы ⇓

Определения

Здесь мы приводим определения, которые встречаются в литературе, и имеют отношение к касательной и нормали. Вывод формул приводится в примере 1 ⇓.

Определение касательной приводится здесь. Уравнение касательной:
.

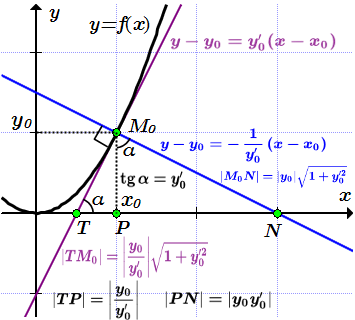
Касательная TM₀, нормаль M₀N, подкасательная TP, поднормаль PN. Нормалью к графику функции в точке называется прямая, перпендикулярная касательной, проведенной через эту точку. Уравнение нормали:
.
Отрезком касательной называют отрезок между точкой пересечения касательной с осью абсцисс и точкой .
.
Отрезком нормали называют отрезок между точкой пересечения нормали с осью абсцисс и точкой .
.
Подкасательной называют отрезок между точкой пересечения касательной с осью абсцисс и проекции точки на эту ось.
.
Поднормалью называют отрезок между точкой пересечения нормали с осью абсцисс и проекции точки на эту ось.
.
Углом между кривыми в точке их пересечения называют угол между касательными к кривым, проведенных через точку .

Полезные формулы из аналитической геометрии

Далее приводятся некоторые сведения из аналитической геометрии, которые могут оказаться полезными при решении задач.

Уравнение прямой, проходящей через две заданные точки и :
.
Здесь – направляющий вектор прямой.

Умножив это уравнение на , получим уравнение прямой в другом виде:
.
Здесь – вектор нормали прямой. Тогда само уравнение означает равенство нулю скалярного произведения векторов и .

Уравнение прямой, проходящей через точку параллельно вектору имеет вид:
.
Вектор называется направляющим вектором данной прямой. Это уравнение можно написать в параметрическом виде, введя параметр t :

Уравнение прямой, проходящей через точку перпендикулярно вектору имеет вид:
.
Вектор называется вектором нормали данной прямой.

Уравнение прямой с угловым коэффициентом k , проходящей через точку :
.
Угол α между прямой и осью x определяется по формуле:
.
Если две прямые взаимно перпендикулярны, то их угловые коэффициенты и связаны соотношением:
.

Уравнение прямой в отрезках, пересекающей оси координат в точках :
.

Примеры решения задач

Все примеры Ниже рассмотрены примеры решений следующих задач.
1. Найти уравнения касательной и нормали к кривой в точке . Найти длины отрезков касательной, нормали, подкасательной и поднормали. Решение ⇓
2. Составить уравнения касательной и нормали к циссоиде, заданной в параметрическом виде
, проведенных в точке . Решение ⇓
3. Заданной в неявном виде . Решение ⇓
4. Найти угол между кривыми и Решение ⇓

Пример 1

Составить уравнения касательной и нормали к кривой в точке . Найти длины отрезков касательной, нормали, подкасательной и поднормали.

Находим значение функции при :
.

Находим производную:
.
Находим производную в точке :
;
.

Находим уравнение касательной по формуле (2):
;
;
;
– уравнение касательной.
Строим касательную на графике. Поскольку касательная – это прямая, то нам нужно знать положения двух ее точек, и провести через них прямую.
При ;
при .
Проводим касательную через точки и .

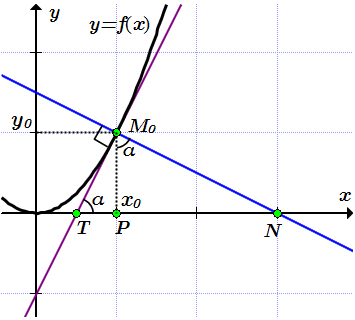
Касательная и нормаль к графику функции y=x 2 в точке M₀(1;1).

Найдем угол α между касательной и осью абсцисс по формуле (1):
.
Подставляем :
;
.

Находим уравнение нормали по формуле (3):
;
;
;
;
;
– уравнение нормали.
Строим нормаль по двум точкам.
При ;
при .
Проводим нормаль через точки и .

Находим длину отрезка касательной . Из прямоугольника имеем:
.
Поясним использованную формулу. Поскольку , то . Тогда
.
Подставляем :
.

Находим длину отрезка подкасательной . Из прямоугольника имеем:
.
Подставляем :
.

Находим длину отрезка нормали . Поскольку и , то треугольники и подобны. Тогда . Из прямоугольника имеем:
.
Подставляем :
.

Находим длину отрезка поднормали . Из прямоугольника имеем:
.

Примечание.
При выводе формул, можно сначала определить длины отрезков подкасательной и поднормали, а затем из прямоугольников, по теореме Пифагора, найти длины отрезков касательной и нормали:
;
.

Уравнение касательной: ; уравнение нормали: ;
длина отрезка касательной: ; длина отрезка нормали: ; длина подкасательной: ; длина поднормали: .

Пример 2

Составить уравнения касательной и нормали к циссоиде, заданной в параметрическом виде , проведенных в точке .

Находим значения переменных при .
;
.
Обозначим эту точку как .

Находим производные переменных x и y по параметру t .
;
;
;
;
.

Подставляя , находим производную y по x в точке .
.

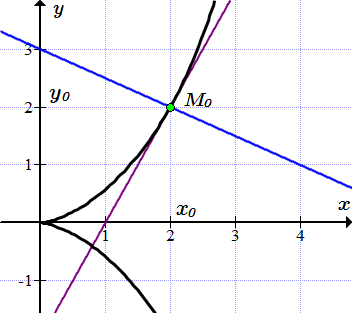
Касательная и нормаль к циссоиде в точке (2;2).

Применяя формулу (2), находим уравнение касательной к циссоиде, проходящей через точку .
;
;
;
.

Применяя формулу (3), находим уравнение нормали к циссоиде в точке .
;
;
;
.

Уравнение касательной: .
Уравнение нормали: .

Пример 3

Составить уравнения касательной и нормали к циссоиде, заданной в неявном виде:
(П3) ,
проведенных в точке .

Для получения уравнение касательной и нормали, нам нужно знать значение производной функции в заданной точке. Функция (П3) задана неявно. Поэтому применяем правило дифференцирования неявной функции. Для этого дифференцируем (П3) по x , считая, что y является функцией от x .
;
;
;
.
Отсюда
.

Находим производную в заданной точке, подставляя .
;
.

Находим уравнение касательной по формуле (2).
;
;
;
.

Находим уравнение нормали по формуле (3).
;
;
;
.

Касательная и нормаль к циссоиде изображены на рисунке ⇑.

Уравнение касательной: .
Уравнение нормали: .

Пример 4

Найти угол между кривыми и .

Найдем множество точек пересечения кривых, решая систему уравнений.

Левые части равны. Приравниваем правые части и выполняем преобразования.
;
(П4) .
Поскольку функция строго монотонна, то уравнение (П4) имеет один корень:
.
При . Кривые пересекаются в единственной точке . Обозначим ее как , где .

Введем обозначения для функций, с помощью которых заданы кривые:
.
Найдем их производные.
;
.
Найдем значения производных в точке , подставляя .
;
.

Ниже приводятся графики функций ⇓ и вывод формулы угла между кривыми.

Вывод формулы для угла между кривыми

Изложим вывод формулы (4). Для иллюстрации используем только что рассмотренный пример ⇑, в котором .

Рассмотрим две кривые, заданные уравнениями и , и пересекающиеся в некоторой точке . Докажем, что угол между кривыми определяется по формуле (4):
, где .
Или ;
при .

Проведем касательные к графикам функций в точке . Углы, которые образуют касательные с осью x обозначим как и . За положительное направление выберем направление против часовой стрелки. На рисунке . Считаем, что значения углов принадлежат интервалам . Согласно геометрическому смыслу производной,
.

В аналитической геометрии принято, что угол φ между прямыми равен наименьшему значению угла между ними.
Если , то ;
если , то .
Таким образом величина угла φ между касательными может находиться только в пределах
(Ф2) .

На рисунке угол между лучами и больше 90°, а между лучами и – меньше. Поэтому .

При доказательстве мы будем использовать соотношение:
, которое выполняется при .
Тогда в силу (Ф2),
.
Случай мы рассмотрим отдельно.

1) Пусть .
Тогда угол между прямыми . И мы имеем:
.
В конце мы подставили (Ф1).

2) Пусть .
Тогда ; . Поэтому . Это можно записать так: . Также применим формулу: . В результате получаем:

Этот случай изображен на рисунке ⇑.

3) Пусть .
При этом касательные взаимно перпендикулярны, . В этом случае , что указано в (4).

Использованная литература:
П.Е. Данько, А.Г. Попов, Т.Я.Кожевникова. Высшая математика в упражнениях и задачах. Часть 1. Москва, Высшая школа, 1980.
Л.Д. Кудрявцев, А.Д. Кутасов, В.И. Чехлов, М.И. Шабунин. Сборник задач по математическому анализу. Том 1. Москва, Физматлит, 2003.

Автор: Олег Одинцов . Опубликовано: 30-06-2021

источники:

http://function-x.ru/derivative_and_tangent.html

http://1cov-edu.ru/mat-analiz/proizvodnaya/kasatelnaya-i-normal-k-grafiku-funktsii/