Уравнение касательной к кривой сга

Уравнение касательной к кривой сга

Абсциссы стационарных точек функции равны
Абсциссы стационарных точек функции равны
В области определения число точек экстремума функции равно
В области определения число точек экстремума функции равно
Даны функции: 1) ; 2) ; 3) ; 4) . Из них четными являются
Даны функции: 1) ; 2) ; 3) ; 4) . Из них нечетными являются
Дифференциал функции равен
Дифференциал функции равен
Дифференциал функции равен
Дифференциал функции равен
Дифференциал второго порядка функции равен
Дифференциал второго порядка функции равен
Дифференциал первого порядка функции равен
Для того, чтобы стационарная точка дважды дифференцируемой функции была точкой максимума, достаточно чтобы
Для того, чтобы стационарная точка дважды дифференцируемой функции была точкой локального минимума, достаточно чтобы
Для функции односторонние пределы в точке равны
Для функции односторонние пределы в точке равны
Для функции односторонние пределы в точке равны
Для функции односторонние пределы в точке равны
Для функции односторонние пределы в точке равны
Если — точка экстремума дифференцируемой функции , тогда
Заданы функции: 1) ; 2) ; 3) ; 4) . Взаимнооднозначное соответствие между областью определения и областью значений задают функции с номерами
Касательная к кривой в точке пересекает ось под углом
Касательная к кривой в точке пересечения с осью параллельна
Касательная к кривой в точке пересечения с осью имеет вид
Касательная к кривой в точке параллельна
Касательная к кривой в точке параллельна
Касательная к кривой в точке параллельна
Касательная к кривой параллельна оси в точке с абсциссой
Касательная к кривой в точке с осью образует угол
Касательная к кривой параллельна прямой в точке с абсциссой
Касательная к кривой в точке с абсциссой параллельна
Касательная к кривой параллельна оси в точке с абсциссой
Касательная к кривой параллельна оси в точке с абсциссой
Касательная к кривой параллельна оси в точке с абсциссой
Кривая имеет касательную, параллельную оси в точке с абсциссой
Кривая имеет касательную, параллельную прямой , в точке с абсциссой
Множество является областью определения функции , а множество — областью значений этой функции. Областью определения функции , обратной к данной является множество
Множество является областью определения, а множество — областью значений функции . Областью определения функции , обратной к данной является множество
Наибольшее значение функции на отрезке равно
Наибольшее значение функции на отрезке равно
Наибольшее значение, монотонно возрастающей на отрезке функции , равно
Наибольшее значение, монотонно убывающей на отрезке функции , равно
Наименьшее значение функции на отрезке равно
Наименьшее значение функции на отрезке равно
Наименьшее значение, монотонно возрастающей на отрезке функции , равно
Наименьшее значение, монотонно убывающей на отрезке функции , равно
Областью определения функции является множество
Областью определения функции является множество
Областью определения функции является множество
Областью определения функции является множество
Областью определения функции является множество
Правило Лопиталя применяется непосредственно для раскрытия неопределенности типа
Приращение и дифференциал функции при и равны соответственно
Производная функции равна
Производная функции равна
Производная функции равна
Производная функции равна
Производная функции равна
Производная функции равна
Производная функции равна
Производная функции равна
Производная функции равна
Производная второго порядка функции равна
Производная второго порядка функции равна
Производная второго порядка функции равна
Производная второго порядка функции равна
Производная второго порядка функции равна
Производная второго порядка функции равна
Производная функции равна
Разность значений функции в точках локального максимума и локального минимума равна
Разность значений функций в точках локального максимума и локального минимума равна
Разность между наибольшим и наименьшим значениями функции на отрезке равна
Среди функций 1) 2) 3) ; 4) 5) в точке разрыв первого рода и скачек имеют функции
Среди функций 1) 2) 3) ; 4) 5) в точке разрыв второго рода имеют функции
Среди функций 1) 2) 3) ; 4) 5) в точке устранимый разрыв имеют функции
Среди функций 1) 2) 3) 4. 5) в точке разрыв второго рода имеют функции
Среди функций 1) 2) 3) 4) 5) в точке разрыв первого рода и скачек имеют функции
Среди функций: 1) ; 2) ; 3) ; 4) на интервале возрастающими являются
Среди функций: 1) ; 2) ; 3) ; 4) ; 5) ; 6) взаимно обратными являются следующие пары
Среди функций: 1) ; 2) ; 3) ; 4) ; 5) ; 6) взаимно обратными являются следующие пары
Среди функций: 1) 2) 3) 4) 5) в точке устранимый разрыв имеют функции
Точка является точкой локального минимума функции
Точка называется критической точкой функции , если
Точка называется стационарной точкой функции , если
Точка является точкой экстремума функции
Точка является точкой локального минимума функции
Точка является точкой локального максимума функции
Тригонометрические функции имеют следующую четность
Угловой коэффициент касательной к кривой в точке равен
Угловой коэффициент касательной к кривой в точке равен
Угловой коэффициент касательной к кривой в точке равен
Угловой коэффициент касательной к кривой в точке с абсциссой равен
Уравнение касательной к кривой в точке имеет вид
Уравнение касательной к кривой в точке имеет вид
Уравнение касательной к кривой в точке имеет вид
Уравнение касательной к кривой в точке имеет вид
Уравнение касательной к кривой в точке имеет вид
Уравнение касательной к кривой в точке с абсциссой имеет вид
Функция обладает следующими свойствами
Функция обладает следующими свойствами
Функция обладает следующими свойствами
Функция обладает следующими свойствами
Функция при обладает следующими свойствами
Функция при обладает следующими свойствами
Функция при обладает следующими свойствами
Функция при обладает следующими свойствами
Функция возрастает на интервале
Функция убывает на интервале
Функция возрастает на интервале
Функция убывает на интервале
Функция на отрезке не имеет стационарных точек при
Функция обладает следующими свойствами
Функция в точке имеет
Функция обладает следующими свойствами
Функция в точке терпит разрыв
Функция в точке
Функция в точке имеет
Функция обладает следующими свойствами
Функция будет непрерывной при значении параметра равном
Функция в точке имеет
Функция будет непрерывной при значении параметра равном
Функция будет непрерывной при
Функция будет непрерывной при
Функция будет непрерывной при
Функция будет непрерывной при
Функция будет непрерывной при
Функция будет непрерывной при
Функция будет непрерывной при
, тогда производная равна
возрастает на интервале

Уравнение касательной к кривой сга

Длину дуги кривой от точки с абсциссой до точки с абсциссой вычисляют с помощью интеграла
2
Абсциссы стационарных точек функции равны
Абсциссы стационарных точек функции равны
В области определения число точек экстремума функции равно
В области определения число точек экстремума функции равно
Все значения равны
Все значения равны
Все значения равны
Выражение в алгебраической форме имеет вид
Выражение в алгебраической форме имеет вид
Выражение в алгебраической форме имеет вид
Выражение в алгебраической форме имеет вид
Выражение в алгебраической форме имеет вид
Градиент функции в точке равен
Градиент функции в точке равен
Градиент функции в точке равен
Даны функции: 1) ; 2) ; 3) ; 4) . Из них четными являются
Даны функции: 1) ; 2) ; 3) ; 4) . Из них нечетными являются
Действительные решения уравнения равны
Действительные решения уравнения равны
Действительные решения уравнения равны
Действительные решения уравнения равны
Действительные решения уравнения равны
Дифференциал функции равен
Дифференциал функции равен
Дифференциал функции равен
Дифференциал функции равен
Дифференциал второго порядка функции равен
Дифференциал второго порядка функции равен
Дифференциал первого порядка функции равен
Длина дуги кривой y=lnx от точки М(1,0) до точки М(е,1) вычисляется с помощью интеграла
Длина дуги кривой от точки А(0,1) до точки B(1,2) вычисляют с помощью интеграла
Длина дуги параболы от начала координат до точки А(1,2) вычисляют с помощью интеграла
Длина дуги параболы с концами в точках О(0,0) и А(2,4) вычисляют с помощью интеграла
Длина дуги полукубической параболы от начала координат до начала координат до точки А(4,8) вычисляют с помощью интеграла
Длину дуги параболы , отсекаемую осями координат, вычислят с помощью интеграла
Для того, чтобы стационарная точка дважды дифференцируемой функции была точкой максимума, достаточно чтобы
Для того, чтобы стационарная точка дважды дифференцируемой функции была точкой локального минимума, достаточно чтобы
Для функции односторонние пределы в точке равны
Для функции односторонние пределы в точке равны
Для функции односторонние пределы в точке равны
Для функции односторонние пределы в точке равны
Для функции односторонние пределы в точке равны
Достаточное условие экстремума дважды дифференцируемой функции в стационарной точке заключается в следующем
Если — точка экстремума дифференцируемой функции , тогда
Заданы функции: 1) ; 2) ; 3) ; 4) . Взаимнооднозначное соответствие между областью определения и областью значений задают функции с номерами
Значение выражения в алгебраической форме равно
Значение выражения в алгебраической форме равно
Значение выражения в алгебраической форме равно
Значение выражения в алгебраической форме равно
Значение разности в точке для функции равно
Значение разности в точке для функции равно
Значение суммы в точке для функции равно
Интеграл равен сумме интегралов:
Интеграл равен сумме интегралов
Интеграл равен сумме интегралов
Интеграл заменой переменной t=sinx сводится к интегралу
Интеграл заменой переменной t=cosx сводится к интегралу
Касательная к кривой в точке пересечения с осью параллельна
Касательная к кривой в точке пересекает ось под углом
Касательная к кривой в точке пересечения с осью имеет вид
Касательная к кривой в точке параллельна
Касательная к кривой в точке параллельна
Касательная к кривой в точке параллельна
Касательная к кривой параллельна оси в точке с абсциссой
Касательная к кривой в точке с осью образует угол
Касательная к кривой параллельна прямой в точке с абсциссой
Касательная к кривой в точке с абсциссой параллельна
Касательная к кривой параллельна оси в точке с абсциссой
Касательная к кривой параллельна оси в точке с абсциссой
Касательная к кривой параллельна оси в точке с абсциссой
Кривая имеет касательную, параллельную оси в точке с абсциссой
Кривая имеет касательную, параллельную прямой , в точке с абсциссой
Матрица для функции имеет вид
Матрица для функции имеет вид
Матрица вторых производных для функции равна
Множество является областью определения функции , а множество — областью значений этой функции. Областью определения функции , обратной к данной является множество
Множество является областью определения, а множество — областью значений функции . Областью определения функции , обратной к данной является множество
Наибольшее значение функции на отрезке равно
Наибольшее значение функции на отрезке равно
Наибольшее значение, монотонно возрастающей на отрезке функции , равно
Наибольшее значение, монотонно убывающей на отрезке функции , равно
Наименьшее значение функции на отрезке равно
Наименьшее значение функции на отрезке равно
Наименьшее значение, монотонно возрастающей на отрезке функции , равно
Наименьшее значение, монотонно убывающей на отрезке функции , равно
Необходимое условие экстремума функции заключается в следующем
Область определения функции задается неравенствами
Область определения функции задается неравенствами
Область определения функции задается неравенством
Область определения функции задается неравенствами
Область определения функции задается неравенствами
Область определения функции задается неравенствами
Область определения функции задается неравенствами
Область определения функции задается неравенствами
Область определения функции задается неравенством
Область определения функции задается неравенством
Область определения функции задается неравенствами
Область определения функции задается неравенствами
Область определения функции задается неравенством
Область определения функции задается неравенствами
Область определения функции задается неравенством
Областью определения функции является множество
Областью определения функции является множество
Областью определения функции является множество
Областью определения функции является множество
Областью определения функции является множество
Объем тела, образованного вращением вокруг оси ОУ фигуры, ограниченной линиями вычисляют с помощью интеграла
Объем тела, образованного вращением вокруг оси ОУ фигуры, ограниченной линиями , х=0, х=1, у=0, вычисляют с помощью интеграла
Объем тела, образованного вращением вокруг оси ОХ одной полуволны синусоиды , равен
Объем тела, образованного вращением вокруг оси ОХ фигуры, ограниченной линиями , у=0, х=0, вычисляют с помощью интеграла
Объем тела, образованного вращением вокруг оси ОХ фигуры, ограниченной линиями , у=1, х=0, равен
Объем тела, образованного вращением вокруг оси ОХ фигуры, ограниченной линиями , х=1, х=0, равен
Объем тела, образованного вращением вокруг оси ОХ фигуры, ограниченной линиями , у=0, х=1, х=2 вычисляют с помощью интеграла
Объем тела, образованного вращением вокруг оси ОХ фигуры, ограниченной параболой и осью ОХ вычисляют с помощью определенного интеграла
Объем тела, образованного вращением вокруг оси ОХ фигуры, ограниченной линиями , х=0, х=1, у=0, равен
Объем тела, образованного вращения вокруг оси ОХ фигуры, ограниченной параболой и осью ОХ, равен
Первообразной для функции является функция
Площадь криволинейной трапеции, ограниченной кривой , линиями х=0, х=1, у=0, равна
Площадь криволинейной трапеции, ограниченной линиями , вычисляют с помощью определенного интеграла
Площадь криволинейной трапеции, ограниченной линиями , у=0, , х=3 равна
Площадь криволинейной трапеции, ограниченной линиями , у=0, , х=3 равна
Площадь криволинейной трапеции, ограниченной одной полуволной синусоиды и осью ОХ равна
Площадь области, ограниченной линиями , вычисляют с помощью определенного интеграла
Площадь области, ограниченной линиями , вычисляют с помощью определенного интеграла
Площадь области, ограниченной линиями равна
Площадь области, ограниченной линиями , вычисляют с помощью определенного интеграла
Площадь области, ограниченной линиями и , вычисляется с помощью определенного интеграла
Площадь области, ограниченной линиями , вычисляют с помощью определенного интеграла
Площадь параболического сегмента, ограниченного параболой и осью ОХ, равна
Площадь трапеции, ограниченной линиями , , х=2, у=0 равна
Площадь фигуры, ограниченной одной полуволной косинусоиды и осью ОХ равна
Полный дифференциал функции в точке равен
Полный дифференциал функции равен
Полный дифференциал функции в точке равен
Полный дифференциал функции в точке равен
Полный дифференциал функции равен
Полный дифференциал функции в точке равен
Полный дифференциал функции в точке равен
Полный дифференциал функции в точке равен
Полный дифференциал функции в точке равен
Правило Лопиталя применяется непосредственно для раскрытия неопределенности типа
Приращение и дифференциал функции при и равны соответственно
Произведение в алгебраической форме имеет вид
Производная функции равна
Производная функции равна
Производная функции равна
Производная функции равна
Производная функции равна
Производная функции равна
Производная функции равна
Производная функции равна
Производная функции равна
Производная второго порядка функции равна
Производная второго порядка функции равна
Производная второго порядка функции равна
Производная второго порядка функции равна
Производная второго порядка функции равна
Производная второго порядка функции равна
Производная функции равна
Разложение дроби на простейшие дроби с неопределенными коэффициентами имеет вид
Разность в алгебраической форме имеет вид
Разность — в алгебраической форме имеет вид
Разность значений функции в точках локального максимума и локального минимума равна
Разность значений функций в точках локального максимума и локального минимума равна
Разность между наибольшим и наименьшим значениями функции на отрезке равна
Среди функций 1) 2) 3) ; 4) 5) в точке разрыв первого рода и скачек имеют функции
Среди функций 1) 2) 3) ; 4) 5) в точке разрыв второго рода имеют функции
Среди функций 1) 2) 3) ; 4) 5) в точке устранимый разрыв имеют функции
Среди функций 1) 2) 3) 4. 5) в точке разрыв второго рода имеют функции
Среди функций 1) 2) 3) 4) 5) в точке разрыв первого рода и скачек имеют функции
Среди функций: 1) ; 2) ; 3) ; 4) на интервале возрастающими являются
Среди функций: 1) ; 2) ; 3) ; 4) ; 5) ; 6) взаимно обратными являются следующие пары
Среди функций: 1) ; 2) ; 3) ; 4) ; 5) ; 6) взаимно обратными являются следующие пары
Среди функций: 1) 2) 3) 4) 5) в точке устранимый разрыв имеют функции
Стационарная точка функции будет точкой максимума функции, если в точке
Стационарная точка функции будет точкой минимума функции, если в точке
Стационарная точка функции и значение функции в этой точке равны
Стационарной точкой функции является точка
Стационарной точкой функции является точка
Стационарной точкой функции является точка
Стационарной точкой функции является точка
Стационарными точками функции являются точки
Сумма равна
Сумма + в алгебраической форме имеет вид
Точка является точкой локального минимума функции
Точка называется критической точкой функции , если
Точка называется стационарной точкой функции , если
Точка является точкой экстремума функции
Точка является точкой локального минимума функции
Точка является точкой локального максимума функции
Точкой максимума функции является точка
Точкой максимума функции является точка
Точкой максимума функции является точка
Точкой минимума функции является точка
Точкой минимума функции является точка
Точкой минимума функции является точка
Точкой минимума функции является точка
Точкой минимума функции является точка
Тригонометрическая форма комплексного числа имеет вид
Тригонометрическая форма комплексного числа имеет вид
Тригонометрическая форма комплексного числа имеет вид
Тригонометрическая форма комплексного числа имеет вид
Тригонометрическая форма комплексного числа имеет вид
Тригонометрическая форма комплексного числа равна
Тригонометрическая форма комплексного числа имеет вид
Тригонометрические функции имеют следующую четность
Угловой коэффициент касательной к кривой в точке равен
Угловой коэффициент касательной к кривой в точке равен
Угловой коэффициент касательной к кривой в точке равен
Угловой коэффициент касательной к кривой в точке с абсциссой равен
Уравнение касательной к кривой в точке имеет вид
Уравнение касательной к кривой в точке имеет вид
Уравнение касательной к кривой в точке имеет вид
Уравнение касательной к кривой в точке имеет вид
Уравнение касательной к кривой в точке имеет вид
Уравнение касательной к кривой в точке с абсциссой имеет вид
Уравнение касательной плоскости к поверхности в точке имеет вид
Уравнение касательной плоскости к поверхности в точке имеет вид
Уравнение касательной плоскости к поверхности в точке имеет вид
Уравнение касательной плоскости к поверхности в точке имеет вид
Уравнение касательной плоскости к поверхности в точке имеет вид
Уравнение нормали к поверхности в точке имеет вид
Уравнение нормали к поверхности в точке имеет вид
Уравнения линий уровня функции имеют вид
Уравнения линий уровня функции имеют вид
Уравнения линий уровня функции имеют вид
Уравнения линий уровня функции имеют вид
Уравнения линий уровня функции имеют вид
Уравнения линий уровня функции имеют вид
Уравнения линий уровня функции имеют вид
Уравнения линий уровня функции имеют вид
Уравнения линий уровня функции имеют вид
Уравнения линий уровня функции имеют вид
Функция обладает следующими свойствами
Функция обладает следующими свойствами
Функция обладает следующими свойствами
Функция обладает следующими свойствами
Функция при обладает следующими свойствами
Функция при обладает следующими свойствами
Функция при обладает следующими свойствами
Функция при обладает следующими свойствами
Функция возрастает на интервале
Функция убывает на интервале
Функция возрастает на интервале
Функция убывает на интервале
Функция на отрезке не имеет стационарных точек при
Функция обладает следующими свойствами
Функция в точке имеет
Функция обладает следующими свойствами
Функция в точке терпит разрыв
Функция в точке
Функция в точке имеет
Функция обладает следующими свойствами
Функция будет непрерывной при значении параметра равном
Функция в точке имеет
Функция будет непрерывной при значении параметра равном
Функция будет непрерывной при
Функция будет непрерывной при
Функция будет непрерывной при
Функция будет непрерывной при
Функция будет непрерывной при
Функция будет непрерывной при
Функция будет непрерывной при
Функция F(x) называется первообразной для функции f(x) на интервале (a,b), если для всех выполняется равенство
Частное в алгебраической форме имеет вид
Частные производные второго порядка функции равны
Частные производные второго порядка функции равны
Частные производные второго порядка функции равны
Частные производные второго порядка функции равны
Частные производные второго порядка функции равны
Частные производные и полный дифференциал функции равны
Частные производные первого порядка функции равны
Частные производные функции равны
Частные производные функции равны
Частные производные функции равны
Частные производные функции равны
Частные производные функции равны
Частные производные функции равны
Частные производные функции равны
Частные производные функции равны
Частные производные функции равны
Число стационарных точек функции равно
, тогда производная равна
возрастает на интервале

VMath

Инструменты сайта

Основное

Навигация

Информация

Действия

Содержание

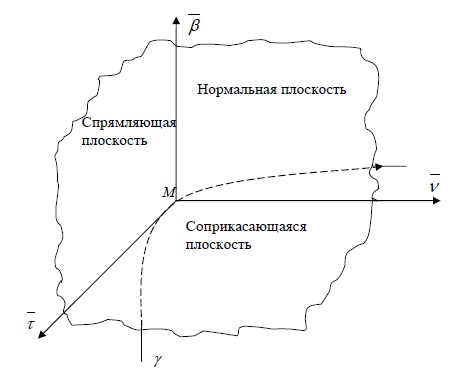
Касательная, нормальная плоскость, соприкасающаяся плоскость, бинормаль, главная нормаль, репер Френе

Краткие теоретические сведения

Кривая в пространстве

Рассмотрим в пространстве гладкую кривую $\gamma$.

Пусть точка $M$ принадлежит данной кривой и отвечает значению параметра $t=t_0$. Тогда радиус-вектор и координаты данной точки равны:

\begin \vec=\vec(t_0), \quad x_0=x(t_0),\, y_0=y(t_0), \, z_0=z(t_0). \end

Пусть в точке $M$ $ \vec(t_0)\neq\vec<0>$, то есть $M$ не является особой точкой.

Касательная к кривой

Касательная к кривой, проведенная в точке $M$, имеет направляющий вектор коллинеарный вектору $\vec(t_0)$.

Пусть $\vec$ — радиус-вектор произвольной точки касательной, тогда уравнение этой касательной имеет вид

Здесь $\lambda\in(-\infty,+\infty)$ — параметр, определяющий положение точки на касательной (то есть разным значениям $\lambda$ будут соответствовать разные значения $\vec$).

Если $\vec=\$, $M = (x(t_0), y(t_0), z(t_0))$, то можно записать уравнение касательной в каноническом виде:

Нормальная плоскость

Плоскость, проходящую через данную точку $M$ кривой $\gamma$ перпендикулярно касательной в этой точке, называют нормальной плоскостью.

Пусть $\vec$ — радиус-вектор произвольной точки нормальной плоскости, тогда ее уравнение можно записать в векторном виде через скалярное произведение векторов $\vec-\vec(t_0)$ и $\vec(t_0)$:

Если расписать покоординатно, то получим следующее уравнение:

\begin x'(t_0)\cdot(X-x(t_0))+y'(t_0)\cdot(Y-y(t_0))+z'(t_0)\cdot(Z-z(t_0))=0. \end

Соприкасающаяся плоскость

Плоскость, проходящую через заданную точку $M$ кривой $\gamma$ параллельно векторам $\vec(t_0)$, $\vec(t_0)$, когда они неколлинеарны, называют соприкасающейся плоскостью кривой.

Если $\vec$ — радиус-вектор произвольной точки соприкасающейся плоскости, то ее уравнение можно записать через смешанной произведение трех компланарных векторов $\vec-\vec(t_0)$, $\vec(t_0)$, $\vec(t_0)$:

Зная координаты точки и векторов, определяющих плоскость, запишем смешанное произведение через определитель. Получим следующее уравнение соприкасающейся плоскости:

\begin \left| \begin X-x(t_0) & Y-y(t_0) & Z-z(t_0) \\ x'(t_0) & y'(t_0) & z'(t_0)\\ x»(t_0) & y»(t_0) & z»(t_0) \\ \end \right|=0 \end

Бинормаль и главная нормаль

Прямая, проходящая через точку $M$ кривой $\gamma$ перпендикулярно касательной к кривой в этой точке, называется нормалью.

Таких кривых можно провести бесконечно много, все они образуют нормальную плоскость. Мы выделим среди нормалей две — бинормаль и главную нормаль.

Нормаль, перпендикулярную соприкасающейся плоскости, называют бинормалью.

Нормаль, лежащую в соприкасающейся плоскости, называют главной нормалью.

Из определения бинормали (перпендикулярна касательной и перпендикулярна соприкасающейся плоскости) следует, что в качестве ее направляющего вектора мы можем взять векторное произведение $ \vec(t_0)\times\vec(t_0)$, тогда ее уравнение можно записать в виде:

Как и раньше, $\vec$ — радиус-вектор произвольной точки бинормали. Каноническое уравнение прямой:

Из определения главной нормали (перпендикулярна касательной и перпендикулярна бинормали) следует, что в качестве ее направляющего вектора можно взять векторное произведение $\vec(t_0) \times\left[\vec(t_0),\vec(t_0)\right]$:

Уравнение в каноническом виде распишите самостоятельно.

Спрямляющая плоскость

Плоскость, проходящую через заданную точку $M$ кривой $\gamma$ перпендикулярно главной нормали, называют спрямляющей плоскостью.

Другое определение: Плоскость, определяемую касательной к кривой и бинормалью в той же точке, называют спрямляющей плоскостью.

Второе определение позволяет записать уравнение спрямляющей плоскости через смешанное произведение трех компланарных векторов, определяющих эту плоскость $\vec-\vec(t_0)$, $\vec(t_0)$, $\vec(t_0)\times\vec(t_0)$: \begin \left(\vec-\vec(t_0),\, \vec(t_0),\, \vec(t_0)\times\vec(t_0)\right)=0. \end Зная координаты соответствующих векторов, можно легко записать это смешанное произведение через определитель, раскрыв который, вы получите общее уравнение спрямляющей плоскости.

Репер Френе

Орт (то есть единичный вектор) касательной обозначим: $$ \vec<\tau>=\frac<\vec(t_0)><|\vec(t_0)|>. $$ Орт бинормали: $$ \vec<\beta>=\frac<\vec(t_0)\times\vec(t_0)><|\vec(t_0)\times\vec(t_0)|>. $$ Орт главной нормали: $$ \vec<\nu>=\frac<\vec(t_0) \times[\vec(t_0),\,\vec(t_0)]><|\vec(t_0) \times [\vec(t_0),\,\vec(t_0)]|>. $$

Правая тройка векторов $\vec<\tau>$, $\vec<\nu>$, $\vec<\beta>$ называется репером Френе.

Решение задач

Задача 1

Кривая $\gamma$ задана параметрически:

Точка $M$, принадлежащая кривой, соответствует значению параметра $t=0$. Записать уравнения касательной, бинормали, главной нормали, нормальной плоскости, соприкасающейся плоскости и спрямляющей плоскости, проведенных к данной кривой в точке $M$. Записать векторы репера Френе.

Решение задачи 1

Задачу можно решать разными способами, точнее в разном порядке находить уравнения прямых и плоскостей.

Начнем с производных.

\begin 1\cdot X+0\cdot Y+1\cdot (Z-1)=0\,\,\ \Rightarrow \,\, X+Z=1. \end

\begin \left| \begin X-0 & Y-0 & Z-1 \\ 1 & 0 & 1\\ 0 & 2 & 1 \\ \end \right|=0 \end Раскрываем определитель, получаем уравнение: \begin -2X-Y+2Z-2=0 \end

\begin 1\cdot X-4\cdot Y-1\cdot (Z-1)=0\,\,\ \Rightarrow \,\, X-4Y-Z+1=0. \end

Поскольку направляющий вектор главной нормали у нас был найден как векторное произведение направляющих векторов касательной и бинормали, тройка $\vec<\tau>$, $\vec<\nu>$, $\vec<\beta>$ не будет правой (по определению векторного произведения вектор $\vec<\tau>\times\vec<\beta>$ направлен так, что тройка векторов $\vec<\tau>$, $\vec<\beta>$, $\vec<\nu>=\vec<\tau>\times\vec<\beta>$

— правая). Изменим направление одного из векторов. Например, пусть

Теперь тройка $\vec<\tau>$, $\vec<\nu>$, $\vec<\tilde<\beta>>$ образует репер Френе для кривой $\gamma$ в точке $M$.

Задача 2

Написать уравнение соприкасающейся плоскости к кривой $$ x=t,\,\, y=\frac<2>,\,\, z=\frac<3>, $$ проходящей через точку $N(0,0,9)$.

Решение задачи 2

Нетрудно заметить, что точка $N$ не принадлежит заданной кривой $\gamma$. Следовательно соприкасающаяся плоскость проведена в какой-то точке $M(t=t_0)\in\gamma$, но при этом плоскость проходит через заданную точку $N(0,0,9)$.

Найдем значение параметра $t_0$.

Для этого запишем уравнение соприкасающейся плоскости, проведенной в произвольной точке $M(t=t_0)$. И учтем, что координаты $N$ должны удовлетворять полученному уравнению.

Соприкасающаяся плоскость определяется векторами $\vec(t_0)$, $\vec(t_0)$, поэтому записываем определитель \begin \left| \begin X-t_0 & Y-t_0^2/2 & Z-t_0^3/3 \\ &&\\ 1 & t_0 & t^2_0 \\ &&\\ 0 & 1 & 2t_0 \end \right|=0 \quad \Rightarrow \end

\begin (X-t_0)\cdot t_0^2 — (Y-t_0^2/2)\cdot 2t_0 + (Z-t_0^3/3)=0. \end Подставляем вместо $X$, $Y$, $Z$ координаты точки $N$: $X=0$, $Y=0$, $Z=9$, упрощаем и получаем уравнение относительно $t_0$: \begin 9-t_0^3/3=0 \quad \Rightarrow \quad t_0=3. \end Подставив найденное $t_0$ в записанное ранее уравнение, запишем искомое уравнение соприкасающейся плоскости: $$ 9X-6Y+Z-9=0. $$

Задача 3

Через точку $P\left(-\frac45,1,2\right)$ провести плоскость, являющуюся спрямляющей для кривой: $$ x=t^2,\,\, y=1+t,\,\, z=2t. $$

Решение задачи 3

Как и в предыдущей задаче нам неизвестны координаты точки, в которой проведена спрямляющая плоскость к заданной кривой. Найдем их.

Спрямляющая плоскость определяется касательной и бинормалью, то есть векторами $\vec(t_0)$ и $\vec(t_0)\times\vec(t_0)$.

Записываем уравнение спрямляющей плоскости: \begin \left| \begin X-t_0^2 & Y-1-t_0 & Z-2t_0 \\ 2t_0 & 1 & 2\\ 0 & 4 & -2 \end \right|= 0 \end

Раскрываем определитель. Подставляем в уравнение координаты точки $P$: $X=-4/5$, $Y=1$, $Z=2$. Упрощаем и получаем уравнение для нахождения $t_0$: \begin 5t_0^2-8t_0-4=0 \,\, \Rightarrow \,\, t_<01>=2,\, t_<02>=-\frac25. \end

Уравнения соприкасающихся плоскостей к заданной кривой, проходящих через $P$, принимают вид: \begin & 5X-4Y-8Z+24=0,\\ & 25X+4Y+8Z=0. \end