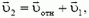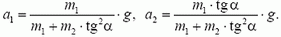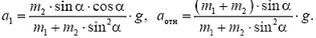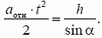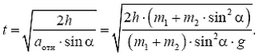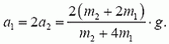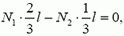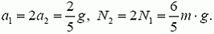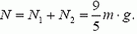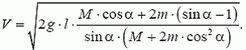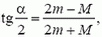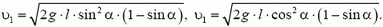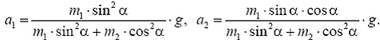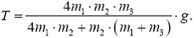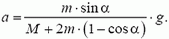Уравнение кинематической связи на ускорения

Кинематические связи

Кинематические связи – уравнения, связывающие между собой кинематические характеристики (координата, скорость, ускорение) тел системы.

Зачастую связи между кинематическими характеристиками различных тел системы возникают благодаря замене реальных тел на физические модели. Физическая модель – это упрощенная версия некоторого явления или тела, которая сохраняет свойства этого явления или тела, исследуемые в данной задаче.

Разберем наиболее распространенные физические модели и кинематические связи, появляющиеся при их использовании.

1. Модель абсолютно твердого тела (АТТ).

Абсолютно твердым телом называется тело, расстояние между любыми двумя точками которого постоянно. Надо понимать, что указанное свойство присуще абсолютно твердому телу всегда, независимо от взаимодействия его с другими телами и от способа движения этого тела. Поэтому если мы рассмотрим две произвольные точки АТТ \(A\) и \(B\) , то в любой момент времени проекции скоростей этих точек \(V_\) и \(V_\) на ось \(x\) , соединяющую \(A\) и \(B\) (см. рисунок 1), должны быть равны друг другу, иначе точка \(B\) будет «убегать» от точки \(A\) , или наоборот, точка \(A\) будет «догонять» точку \(B\) , что невозможно, так как расстояние между ними остается постоянным. Таким образом, в данном случае уравнение кинематической связи связывает проекции скоростей:

Если рассмотреть две оси, — \(y\) и \(z\) — перпендикулярные скоростям \(V_A\) и \(V_B\) точек \(A\) и \(B\) соответственно и проходящие через эти точки, и точку пересечения этих осей обозначить как \(O\) (см. рисунок 2), то, записывая аналогичные (1) уравнения кинематической связи для точек \(O\) и \(A\) на оси \(y\) и \(O\) и \(B\) на оси \(z\) , получим:

Отсюда следует, что скорость точки \(O\) равна нулю: \(V_O=0\) . Такой показатель скорости, а также то обстоятельство, что вокруг точки \(O\) в данный момент происходит вращение, позволяют назвать точку \(O\) мгновенным центром вращения (МЦВ) изучаемого нами тела. Стоит понимать, что с течением времени положение МЦВ в пространстве способно изменяться, и к тому же он не обязан быть одной из точек тела и может лежать вне его (например, МЦВ колеса автомобиля при торможении).

В силу того, что тело вращается вокруг точки \(O\) , для описания его вращения можно использовать понятия угла поворота \(φ\) , угловой скорости \(ω\) и углового ускорения \(ε\) . Учитывая тот факт, что расстояние между любыми двумя точками тела постоянно, для любых двух точек \(A\) и \(B\) , находящихся на одинаковом расстоянии от МЦВ, мы вправе записать:

а для любых двух точек \(B\) и \(C\) , лежащих на одной прямой с точкой \(O\) на расстояниях \(OB=r\) и \(OC=R\) , следующее:

Выражения (2) и (3), как и предыдущие, являются уравнениями кинематической связи. Геометрическая интерпретация уравнения (3) представлена на рисунке 2: скорости и расстояния являются катетами подобных прямоугольных треугольников.

2. Нерастяжимая нить.

Нерастяжимая нить – это частный случай, разновидность абсолютно твердого тела, в которой расстояние между точками сохраняется вдоль единственного направления – контура нити. Для этой модели равными будут проекции скоростей любых двух точек \(A\) и \(B\) на направление нити в данных точках, что является следствием уравнения (1):

Разберем пример задачи с использованием кинематических связей.

Задача 1 («3800 задач по физике для школьников и поступающих в вузы», 1.90º). Тяжелый ящик перемещают с помощью двух тракторов, движущихся со скоростями \(\overrightarrow \) и \(\overrightarrow \) , образующими угол \(α\) . Как направлена и чему равна скорость ящика в тот момент, когда канаты натянуты и параллельны векторам \(\overrightarrow \) и \(\overrightarrow \) ?

Решение задачи 1.

Точка \(O\) (см. рисунок 4) является точкой ящика, движущегося поступательно, поэтому для определения скорости ящика достаточно найти скорость этой точки. В то же время \(O\) — это точка обоих канатов, поэтому ее скорость \(v\) удовлетворяет двум уравнениям кинематической связи, для каждого из канатов. Введя угол \(β\) между скоростями \(v\) и \(v_1\) , можно записать эти уравнения в виде:

\(\begin v_2=vcos(α-β)=v(cosα \ cosβ+sinα \ sinβ), \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ v_1=vcosβ\\ \end\) (4)

Разделив первое уравнение системы (4) на второе, получим:

Особенно важными являются задачи, в которых фигурируют системы блоков. Написание уравнения кинематической связи при их решении является нетривиальной проблемой. Рассмотрим два основных способа получения уравнения кинематической связи на примере простейшей задачи с блоками.

Задача 2 («Задачи по физике» под ред. О.Я. Савченко, 1.5.1.).

Скорость груза \(A\) (см. рисунок 5) равна \(v_A\) . Чему равна скорость груза \(B\) ?

Решение задачи 2.

Способ 1. Уравнение длины нити.

Введем ось \(x\) , направленную, как на рисунке 6. Введем обозначения: \(x_1\) – координата подвижного блока, \(x_2\) – координата неподвижного блока, \(x_B\) – координата груза \(B\) . Тогда, приняв длину зеленой нити за \(L\) , рассмотрим два близких момента времени \(t\) и \(t’\) ( \(t’-t=∆t→0\) ) и запишем:

\(\begin L = x_1 + (x_1 — x_2) + (x_B — x_2) + πR_1 + πR_2, \\ L = > + (> — x_2) + (> — x_2) + πR_1 + πR_2 \\ \end\) , (5)

где \(R_1\) и \(R_2\) – радиусы блоков. Вычитаем из первого уравнения системы (5) второе и делим результат на \(∆t\) . Получаем:

Таким образом, мы вывели уравнение кинематической связи (6) для грузов \(A\) и \(B\) , где \(v_A\) и \(v_B\) – проекции скоростей грузов на ось \(x\) (то есть уравнение (6) связывает также направления скоростей грузов). Аналогичную связь можно записать и для ускорений грузов, если рассмотреть изменение скорости за некоторый период времени точно так же, как мы рассматривали изменение координаты.

Способ 2. Метод малых (виртуальных) перемещений.

Представим мысленно, что за некоторый малый промежуток времени \(∆t\) груз \(A\) сместился вниз на расстояние \(∆x\) (см. рисунок 7). Для того чтобы такое смещение произошло, вертикальные участки зеленой нити должны увеличиться на \(∆x\) справа и слева от подвижного блока. В нашей системе длина нити в левой части системы увеличилась на \(2∆x\) . Из-за этого в силу нерастяжимости нити длина нити в правой части системы должна уменьшиться на \(2∆x\) , а это означает, что груз \(B\) за интервал времени \(∆t\) сместится вверх на расстояние \(2∆x\) . Таким образом:

Разделив обе части уравнения (7) на \(∆t\) , получим:

Мы получили уравнение кинематической связи, аналогичное уравнению (6), но в этот раз не учитывающее направление скоростей. Направление скоростей мы учли при выводе этого уравнения.

Список использованной литературы:

1. «3800 задач по физике для школьников и поступающих в вузы».
2. «Задачи по физике» под редакцией О.Я. Савченко.

Задачи для самостоятельного решения:

1) «Задачи по физике» под редакцией О.Я. Савченко.

1.5.4, 1.5.5*, 1.5.9*, 1.5.14*, 1.5.16

2) «Задачи Московских городских олимпиад по физике. 1986-2005» Варламов С.Д. и др.

3) «1001 задача по физике с решениями» Гельфгат И.М. и др.

Вопросы по содержанию статьи:

1) Выберите верное уравнение кинематической связи для двух точек АТТ, изображенного на рисунке.

2) Где находится МЦВ колеса, движущегося горизонтально без проскальзывания?

II. \(B\) .

3) Зависит ли положение МЦВ тела в пространстве от системы отсчета, в которой мы рассматриваем движение данного тела?

Черноуцан А.И. Кинематические связи в задачах динамики // Квант

Черноуцан А.И. Кинематические связи в задачах динамики // Квант. — 1988. — № 2. — С. 57-62.

По специальной договоренности с редколлегией и редакцией журнала «Квант»

В задачах по механике часто встречается ситуация, когда движение тел не является свободным. Ограничения могут создавать твердые поверхности, нерастяжимые нити, жесткие стержни и т. п.

В простейших случаях мы учитываем подобные ограничения автоматически, часто даже не оговаривая их существования. Например, ускорение тела на плоскости мы направляем вдоль плоскости (учитывая наличие твердой поверхности), скорости буксира и баржи считаем одинаковыми (принимая во внимание присутствие нерастяжимого троса) и т. д. Однако иногда возникает необходимость выразить эти ограничения в виде специального уравнения, которое мы будем называть «кинематической связью». Начнем с такой задачи.

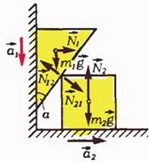
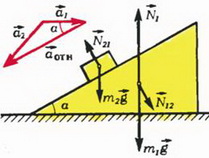
Задача 1. Найдите ускорения призмы массой m₁ и куба массой m₂, изображенных на рисунке 1, а. Трением пренебречь.

Запишем второй закон Ньютона для каждого тела (в проекции на направление, совпадающее с соответствующим ускорением):

Мы учли, что по третьему закону Ньютона 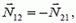т. е. N₁₂ = N₂₁ = N. Написанные два уравнения содержат три неизвестных. Третье уравнение — кинематическая связь между а₁ и a₂ — должно отразить тот факт, что куб и призма остаются все время в контакте друг с другом. Это можно сделать несколькими способами.

1) Рассмотрим два близких положения системы, разделенные промежутком времени Δt (рис. 1, б). В треугольнике ABC сторона АВ равна перемещению призмы Δx₁, а сторона ВС — перемещению куба Δx₂. Имеем

Разделив обе части равенства на Δt, получаем

Так как это соотношение справедливо для произвольного момента времени, из него следует искомое соотношение

Такой подход к получению кинематической связи будем называть прямым методом.

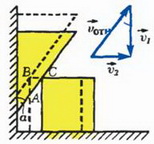
2) Другой способ получения необходимой связи основан на переходе в такую систему отсчета, где условие контакта становится тривиальным. В системе отсчета, связанной с призмой (см. рис. 1, б), скорость куба 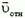направлена вдоль ее поверхности, т. е. под углом α к вертикали. Записывая закон сложения скоростей

из соответствующего векторного треугольника получаем

Решаем совместно уравнения (1)-(3) и находим

В этой задаче второй метод выглядит несколько искусственно. Однако в некоторых случаях именно правильный выбор системы отсчета позволяет существенно упростить проблему кинематических связей. Вот пример.

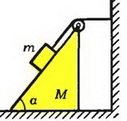
Задача 2. Клин высотой h с углом наклона α стоит на гладкой горизонтальной плоскости (рис. 2). Масса клина m₁. С вершины клина начинает соскальзывать без трения брусок массой m₂. Найдите ускорение клина и время соскальзывания бруска.

Начнем со второго закона Ньютона. Запишем его для клина в проекции на горизонтальное направление, а для бруска пока что в векторной форме:

(5)

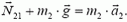
Как и раньше, 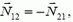т. е. N₁₂ = N₂₁ = N. Выбор направления осей для бруска связан с решением вопроса о кинематической связи.

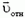
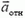
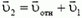
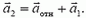
Кинематическая связь между ускорениями должна отразить тот факт, что в процессе движения брусок все время остается на поверхности клина. Записать это в виде прямого уравнения оказывается непросто. Вместо этого перейдем в систему отсчета, связанную с клином. В этой системе скорость бруска и его ускорение направлены вдоль клина. Тогда из закона сложения скоростей получаем закон сложения ускорений (см. рис. 2)

(6)

Отсюда видно, что от неизвестных a₁ и a₂ удобнее перейти к неизвестным a₁ и a_отн, решив тем самым проблему кинематической связи. Подставляя равенство (6) в уравнение (5) и проектируя это уравнение на направления вдоль поверхности клина и перпендикулярно к ней, получаем

Из уравнений (4), (5′) и (5″) находим

Для ответа на второй вопрос задачи нам не надо искать a₁, так как время соскальзывания выражается как раз через a_отн:

Как уже говорилось, ограничение на движение может определяться не только прямым контактом рассматриваемых тел, но и наличием в системе соединительных элементов — стержней, нитей и т. п. В большинстве случаев, даже если в условии это не оговорено, соединительные элементы считаются идеальными, т. е. нити — невесомыми и нерастяжимыми, стержни — невесомыми и абсолютно жесткими, для блоков кроме невесомости предполагается также отсутствие трения на оси. (На самом деле слово «невесомый» означает, что масса данного элемента пренебрежимо мала по сравнению с массами других тел системы, слово «нерастяжимый» — что удлинение элемента мало по сравнению с перемещениями тел системы и т. д.) Перед тем, как разбирать конкретные примеры, выясним, что следует из идеальности соединительных элементов. Рассмотрим три частных случая.

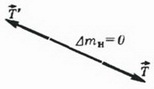
1. Невесомость нити. Напишем второй закон Ньютона для участка нити массой Δm_н (рис. 3, а):

Так как Δm_н = 0, то T – T´, т. е. сила натяжения не меняется вдоль нити.

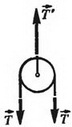
2. Невесомость подвижного блока и отсутствие трения на его оси. Для раскручивания невесомого блока, в котором нет трения, не нужен вращательный момент. Из этого следует, что натяжение одной и той же нити по обе стороны блока одинаково (рис. 3, б), кроме того

3. Невесомость стержня. Это условие означает, что сумма сил и сумма моментов сил, действующих на стержень, равны нулю. Например, если к стержню приложены две силы, то они равны по модулю, противоположны по направлению и действуют вдоль стержня (рис. 3, в). (В отличие от нити, стержень может быть не только в растянутом, но и в сжатом состоянии.)

Нерастяжимость и жесткость нитей и стержней приводит к появлению кинематических связей, которые мы разберем отдельно в следующих задачах.

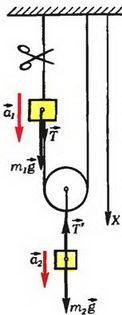
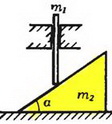
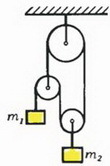
Задача 3. Найдите ускорения грузов массой m₁ и m₂ после перерезания верхней нити (рис. 4). Нити и блок считать идеальными.

Выберем положительное направление оси вертикально вниз и запишем второй закон Ньютона для обоих тел:

(мы учли свойства блока и нити, описанные выше).

Для нахождения кинематической связи между a₁ и а₂ применим, как мы его назвали, прямой метод. Запишем длину нити в виде

где х₁ — координата груза массой m₁, x₂ — координата центра блока, R — его радиус, и учтем, что длина нити при движении грузов не изменяется. Тогда для перемещений грузов получим соотношение

Решая уравнения (7)-(9) совместно, находим

(Обратите внимание на то, что a₁ > g. Подумайте, почему получился такой ответ.)

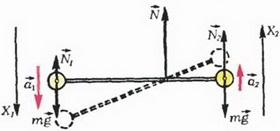
Задача 4. Невесомый стержень с одинаковыми грузами массой m на концах шарнирно закреплен на оси, которая делит его длину в отношении 2:1 (рис. 5). Стержень удерживают в горизонтальном положении и в некоторый момент освобождают. Найдите ускорения грузов сразу после этого, а также давление стержня на ось в этот момент.

Запишем второй закон Ньютона для грузов, выбрав положительные направления осей в сторону соответствующих ускорений:

где N₁ и N₂ — силы, действующие на грузы со стороны стержня. Так как сумма моментов сил, действующих на невесомый стержень, равна нулю, то

где l — длина стержня. Отсюда

Осталось записать кинематическую связь между a₁ и а₂. Для этого изобразим на рисунке 5 положение стержня через малый промежуток времени Δt после начала движения. Из подобия получаем

Решая совместно уравнения (10)-(13), находим

Так как сумма сил, действующих на невесомый стержень, равна нулю, то сила реакции оси (равная по модулю силе давления на ось) равна

Во многих задачах, рассчитанных на применение закона сохранения энергии, требуется найти скорости тел к определенному моменту времени. В этом случае надо установить кинематические связи не между ускорениями, а между скоростями тел. При решении таких задач полезно использовать тот факт, что полная работа, совершаемая любым идеальным соединительным элементом, равна нулю. Физическая причина этого состоит в том, что в таком элементе не может запасаться никакая энергия — ни кинетическая (его масса равна нулю), ни потенциальная (элемент не деформируется).

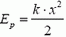
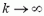
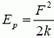
Последнее утверждение требует пояснения. Может показаться, что даже при малой деформации очень жесткого стержня (или другого элемента) потенциальная анергия его деформации может быть велика — ведь она пропорциональна жесткости стержня k. Но если учесть, что сила F = k·x, возникающая при деформации, остается конечной при (она определяется движением тел, закрепленных на стержне), то потенциальная энергия при больших k оказывается очень малой.

Эта и следующая задачи по своему уровню несколько выходят за пределы задач, предлагаемых обычно на вступительных экзаменах в вузы. Однако знакомство с ними для абитуриентов окажется небесполезным.

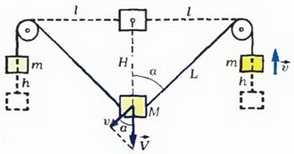
Задача 5. Груз массой М сначала удерживают на уровне блоков, а затем освобождают (рис. 6). Считая нити и блоки идеальными, размеры блоков малыми по сравнению с расстоянием 2l между ними, а массу m грузиков, висящих на концах нитей, известной, найдите скорость груза в тот момент, когда нити составляют угол α с вертикалью. Полученный ответ исследуйте.

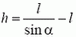
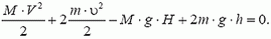
К рассматриваемому моменту груз массой М опустился на H = l·ctg α, а грузики массой m поднялись на каждый. Согласно закону сохранения энергии,

(14)

Для того чтобы найти связь между υ и V, можно, например, применить прямой метод. Из рисунка 6

Дифференцируя по времени (и учитывая, что l´ = 0), находим

Так как L´ = υ, H´ = V, a H/L = cos α, то получаем искомую связь

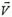
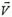
Однако проще получить это соотношение из следующих соображений. Раз расстояние L от груза массой М до блока в рассматриваемый момент увеличивается со скоростью υ (с такой скоростью вытягивается нить), то проекция скорости этого груза на направление нити должна быть равна υ. Учитывая, что скорость направлена вертикально, получаем уравнение (15).

Из уравнений (14) и (15) находим

Выясним, будет ли центральный груз все время опускаться (мы считаем нити очень длинными) или при каком-то α он остановится и начнет подниматься. Уравнение V = 0 (условие остановки) преобразуется к виду

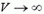
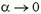
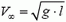
т. е. остановка и обратное движение грузов происходят только при М 2m, то центральный груз будет все время перевешивать и его скорость будет неограниченно возрастать ( при — проверьте это сами). Если же М = 2m, то при опускании центрального груза система все ближе подходит к равновесию, ускорения грузов стремятся к нулю, а их скорости — к предельному значению (убедитесь в этом самостоятельно).

Хотелось бы обратить внимание на то, что при использовании закона сохранения энергии сила натяжения нити вообще не вошла в расчеты.

Последний пример иллюстрирует методы получения кинематических связей при движении твердых стержней (или других твердых связей). Напомним, что при движении твердого тела расстояние между любыми двумя его точками не изменяется.

Задача 6. Невесомый стержень длиной l с грузами массой m на концах соскальзывает по сторонам прямого двугранного угла (рис. 7, а). Найдите скорости грузов в тот момент, когда стержень составляет с горизонтом угол α. Трения нет. В начальный момент стержень находился в вертикальном положении.

Из закона сохранения энергии получаем

(16)

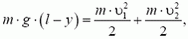
где y = l·sin α — координата второго груза в рассматриваемый момент. Для получения кинематической связи можно применить прямой метод, как это было сделано в предыдущей задаче (проделайте это сами). Быстрее же и нагляднее кинематическая связь получается из таких соображений. Раз расстояние между грузами остается неизменным, то в каждый момент скорость, с которой первый груз «удаляется» от второго, равна скорости, с которой второй груз «приближается» к первому. Иначе говоря, проекции скоростей грузов на стержень в любой момент времени одинаковы (см. рис. 7, a):

Подставляя (17) в (16), находим

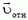
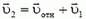
В кинематике твердого тела часто используется «разложение» сложного движения на поступательное и вращательное. Чтобы продемонстрировать этот метод, применим его для получения кинематической связи (17). В системе отсчета, связанной с первым грузом, стержень совершает чисто вращательное движение. Значит, в этой системе скорость второго груза направлена перпендикулярно стержню. Применяя закон сложения скоростей (см. рис. 7, б), получаем соотношение (17).

Может показаться, что найденные выражения для скоростей дают полное решение задачи. Однако в этой задаче содержится поучительный подвох, разбором которого мы и закончим статью.

Решение было бы полным, если бы второй груз не мог оторваться от вертикальной стены. (Для этого можно было бы, например, посадить грузы на гладкие штанги, а стержень присоединить к ним шарнирно). Однако в нашем варианте задачи (см. рис. 7, а) при некотором угле произойдет отрыв второго груза от вертикальной стены, после чего найденный ответ будет неприменим. Дело в том, что горизонтальный импульс системы определяется только движением первого груза, скорость которого, в соответствии с выражением для υ₁, до некоторого угла возрастает, а потом начинает убывать. Это означает, что в какой-то момент должна изменить направление внешняя горизонтальная сила, действующая на систему. Но есть только одна горизонтальная сила — сила реакции вертикальной стенки, которая не может изменить свое направление. Таким образом, в тот момент, когда реакция стенки обращается в нуль, происходит отрыв второго груза от стенки. Дифференцируя выражение для υ₁ по времени, находим, что υ₁ максимальна при sin α = 2/3. При угле 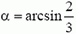и происходит отрыв стержня от вертикальной стенки.

1. Найдите ускорения стержня и клина, изображенных на рисунке 8. Трения нет.

2. Найдите натяжение нити в системе, изображенной на рисунке 9.

3. (для любителей каверз и ловушек). Чему равны ускорения грузов в системе, изображенной на рисунке 10?

4. Найдите ускорение клина на рисунке 11. Трения нет. Указание. Примените метод, использованный при решении задачи 2 в статье.

1.

2.

4.

Приемы решения задач с использованием кинематических связей

МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ГОРОДА КЕРЧИ РЕСПУБЛИКИ КРЫМ «ШКОЛА-ГИМНАЗИЯ №1»

Приемы решения задач с использованием кинематических связей

Подборка задач с примерами решений

Приемы решения задач с использованием кинематических связей

Кинематическими связями называют определенные ограничения свободы передвижения тела или системы тел.

Рассматривая задачи, где такие связи есть, будем придерживаться следующих идей:

Известно из определения, что у твердого тела расстояние между любыми двумя его точками сохраняется в случае движения этого тела (жесткий стержень, натянутая нить А это значит, что с какой скоростью первая точка при движении тела удаляется от второй, с такой же скоростью вторая точка приближается к первой. Следовательно, проекции этих скоростей на линию, соединяющую данные точки, должны быть одинаковыми. Иначе твердое тело деформировалось бы.

Пусть таким твердым телом будет жесткий стержень или натянутая нить. Тогда

использование мгновенного центра вращения.

Что подразумевает переход в такую систему отсчета, в которой есть неподвижная в данный момент времени точка, относительно которой все остальные точки твердого тела движутся. Тогда проектируя скорость точки С и точки В на прямую СВ получаем уравнение вида:

то есть при движении твердого тела скорости всех его точек направлены перпендикулярно прямым, которые соединяют точки с мгновенным центром вращения. Фактически тело проворачивается возле мгновенного центра.

Местоположение мгновенного центра вращения можно находить двумя способами:

если известны скорости двух точек твердого тела и эти скорости не параллельны, то мгновенный центр вращения лежит на пересечении перпендикуляров, проведенным к этим скоростям. Точка С — неподвижна, она является центром вращения, ВС и АС – радиусы окружностей, по которым

вращаются соответственно точки А и В. Скорости х1 и х2 перпендикулярны радиусам.

Так как тело проворачивается возле мгновенного центра, то это означает, что у всех его точек одинаковая угловая скорость. А так как линейная скорость связана с угловой соотношением

то следует пропорция: во сколько раз больше расстояние между данной точкой и мгновенным центром, во столько раз больше ее линейная скорость. Поэтому в случае параллельных скоростей мгновенный центр вращения можно находить через пропорцию скоростей и расстояний.

Если одно тело катится по поверхности другого без проскальзывания, то в точках их соприкосновения и них одинаковая линейная скорость и по величине и по направлению.

Если при движении одного тела по поверхности другого есть проскальзывание, то проекции скоростей соприкасающихся точек на перпендикуляр, восстановленный к этим двум поверхностям, должны быть одинаковы: по оси Y тела должны двигаться только совместно, иначе будет наблюдаться отрыв одного тела от другого.

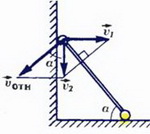
Стержень длиной L шарнирно соединён с муфтами А и В, которые перемещаются по двум взаимно перпендикулярным рейкам. Муфта А движется с постоянной скоростью х1. Найдите зависимость скорости муфты В от угла б.

Использование первой идеи для решения данной задачи: проекции скоростей точек А и В на линию АВ должны быть одинаковыми.

Понятно, что точка В скользит вниз, в то время как точка А движется в горизонтальном направлении. Обозначенные на чертеже углы равны как углы, образованные взаимно перпендикулярными сторонами.

Применение второй идеи для решения данной задачи: использование мгновенного центра вращения.

Представим, что палочка – это элемент, видимая линия, проведенная на большом твердом прозрачном теле. Так как известны скорости двух точек твердого тела, точек А и В, и эти скорости не параллельны, то мгновенный центр вращения лежит на пересечении перпендикуляров, проведенным к этим скоростям. Точка С — мгновенный центр вращения, вокруг которой точка А вращается по окружности радиуса СА, а точка

В вращается по окружности, радиусом ВС. Угловые скорости этих точек равны. Поэтому можно записать:

Еще один способ решения данной задачи: переход в другую систему отсчета.

Перейдем в систему отсчета, которая движется вправо со скоростью V0. (Для перехода от скорости каждой точки надо отнять скорость V0)

Тогда точка А неподвижна, а стенка, и вместе с ней точка В, движется влево со скоростью V0. А так как длина палочки ℓ постоянна, то точка В движется по окружности с линейной скоростью u, которая перпендикулярна радиусу окружности ℓ. Из треугольника скоростей следует:

Палочка АВ длины ℓ движется в плоскости чертежа так, что в данный момент времени скорость её конца А направлена под углом б, а скорость конца В — под углом в к палочке. Величина скорости конца А равна х. Определить величину скорости u конца В. Начертить распределение скоростей вдоль палочки.

На основании первой идеи можно утверждать, что проекции скоростей точек А и В на линию АВ одинаковы. А значит, можно записать:

Скорость точки А и точки В можно разложить на составляющие вдоль палочки и перпендикулярно ей. Тогда движение палочки можно представить как два движения: каждая точка палочки движется поступательно со скоростью u∙Cos в и палочка совершает вращательное движение вокруг точки С. Скорости, перпендикулярные палочке –это линейные скорости. Их величина уменьшается при приближении к точке С. И у точки С только скорость поступательного движения.

Второй способ решения состоит в том, что движение полочки можно рассмотреть только как вращательное движение возле мгновенного центра вращения. Для нахождения мгновенного центра вращения точки С проведем перпендикуляры в точку А к скорости u и в точку В к скорости х. Все точки палочки имеют одинаковую угловую скорость, но линейные скорости у них разные. Чем меньше радиус окружности, по которым они двигаются возле точки С, тем меньше их линейная скорость. То есть для любой точке выполняется х

Лодку подтягивают к крутому берегу высотой h = 3 м с помощью верёвки, выбирая её со скоростью 60 см/с. С какой скоростью двигалась лодка в тот момент, когда верёвка составляла с горизонтом угол 600? Найти также ускорение лодки в этот момент.

На основании первой идеи проекции скорости х и скорости х0 на нерастяжимую веревку должны быть одинаковыми.

Рабочие поднимают груз с помощью двух канатов, за концы которых они тянут с одинаковыми скоростями х. Какую скорость u имеет груз в тот момент, когда угол между канатами, к которым он прикреплён, равен 2б

На основании первой идеи можно утверждать, что проекции скоростей точек А и В на линию АВ одинаковы. Но точка В движется со скоростью х, так как с этой скоростью движется конец каната. Значит, и точка А движется с этой же скоростью. Аналогично для второго каната: точка А движется вдоль него со скоростью х.

Казалось бы, что результирующую скорость точки А можно найти, складывая два вектора х по правилу параллелограмма…

Но этого делать нельзя! Так как в этом случае, если бы б был равен нулю (б=0), тот канаты были бы параллельны, и груз бы двигался со скоростью 2х. А последнее, при наличии неподвижных блоков, невозможно.

Скорость U такова, что скорости х являются ее проекциями на канаты. С учетом этого, можно записать:

Тяжёлый ящик перемещают с помощью двух тракторов, движущихся со скоростями х1 и х2, составляющими угол б. Как направлена и чему равна скорость ящика в тот момент, когда канаты параллельны векторам х1 и х2?

Понятно, что точка А имеет скорость х1 вдоль первого каната и скорость х2 направленную вдоль второго каната. Но, так же, как и в предыдущей задаче, находить результирующую скорость ящика, складывая выше упомянутые скорости по правилу параллелограмма нельзя. В этом случае, если угол б=0, то ящик должен двигаться со скоростью х1+ х1, а это противоречить здравому смыслу.

Следовательно, у результирующей скорости проекции на канаты должны быть равны х1и х2. Проводим перпендикуляры из концов этих векторов и в их пересечение утыкается конец результирующей скорости х, с которой движется ящик. Теперь, зная х1 и х, а так же угол между ними надо найти скорость х. Это геометрическая задача

Точки А, D, С и В лежат на одной окружности и в этой окружности результирующая скорость х – диаметр. Эта окружность описана возле треугольника АВD, в котором известны две стороны х1 и х2, и угол между ними. Тогда по теореме косинусов можно определить сторону ВD:

Известно, что диаметр описанной окружности равен:

Колечки О и О’ надеты на вертикально закреплённые стержни АВ и А’В’. Нерастяжимая нить привязана к кольцу О, пропущена через кольцо О’ и закреплена в точке А’. В тот момент, когда угол AOO’ = б, кольцо О’ движется вниз со скоростью х. Найти скорость u0 кольца О в этот момент.

Так как в колечке О’ нитка преломляется, то использовать первую идею о том, что проекции скорости точки О’ и скорости точки О (проекции скоростей х и u) на нить О’О равны, нельзя.

Используем следующий способ решения: переход в другую систему отсчета.

Перейдем в СО, которая движется со скоростью х вниз ( то есть, от каждой скорости вычитаем скорость х). В такой системе отсчета колечко О’ останавливается, оно неподвижно, а со скоростью х в точке А’ вытягиваем веревку. Тогда веревка в точке О так же движется со скоростью х.

Теперь надо перейти в СО, связанную с землей (надо ко всем скоростям теперь прибавить скорость х, направленную вниз)

Один конец шарнирной конструкции из двух одинаковых звеньев длины 2ℓ закреплён, а дру­гой движется с постоянной скоростью х по прямой, расстояние до которой от неподвижного конца конструкции равно 3ℓ. Найдите ускорение шарнира в тот момент, когда: 1) левое звено горизонтально, 2) скорость шарнира равна нулю.

1). Так как левый конец звена конструкции закреплен в точке О, то шарнир А будет двигаться по окружности радиуса R=2ℓ и в любой момент времени вектор его скорости будет перпендикулярен ОА. В интересующий нас момент времени, когда левое звено ОА горизонтально, скорость шарнира А направлена вверх. И конец правого звена, точка 2, также имеет вертикально направленную скорость х0

На основании первой идеи, из-за не растяжимости правого звена, можно утверждать, что проекции скоростей х и х0 на правое звено (то есть вдоль оси у), равны.

Но это равенство скоростей имеет место только для данного момента времени.

Центростремительное ускорение шарнира А может быть определено по формуле:

И направлено это ускорение вдоль левого звена, то есть по оси х. Но так как скорость шарнира А меняется по величине, а не только по направлению, есть и тангенциальное (касательное) ускорение. Согласно условию, надо найти полное ускорение шарнира А.

Используем переход в другую систему отсчета, которая движется вверх со скоростью х вместе с правым концом правого звена (от каждой скорости надо вычитать х, направленную вверх). Тогда, в этой системе отсчета, точка О движется вниз со скоростью х, а шарнир А неподвижен. Поэтому вектор его ускорения может быть лишь перпендикулярен правому звену.

Вектор полного ускорения шарнира будет точно таким же и в неподвижной системе отсчета. Проекция вектора полного ускорения шарнира на направление левого звена (на ось х) представляет собой центростремительное ускорение, и равна:

Значит, вектор полного ускорения шарнира в момент времени, когда левое звено горизонтально, будет равен:

2). В момент времени, когда скорость шарнира А равна нулю, правое звено будет горизонтально. А вектор ускорения шарнира будет перпендикулярен неподвижному левому звену (рис. б).

Составляющая ускорения шарнира на правое звено будет равна

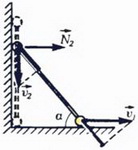
Два стержня длины L соединены шарнирно. Свободный конец одного из стержней шарнирно прикреплён к стене, а свободный конец другого стержня двигают перпендикулярно стене с постоянной по величине скоростью х0. Найти величину и направление вектора ускорения шарнира, соединяющего стержни, в момент, когда угол между стержнями равен 2а.

У левой палочки ее правый конец движется со скоростью х, которая перпендикулярно этой палочке. У правой палочки по условию скорость х0 направлена горизонтально.

На основании первой идеи, из-за не растяжимости стороны АВ, можно утверждать, что проекции скоростей х и х0 на АВ равны.

Тогда

Определяем проекции ускорения на координатные оси. На ось х:

Чтобы найти проекцию ускорения на вторую ось, перейдем в СО, которая движется вправо со скоростью х0.Тогда точка В неподвижна, а стенка движется влево со скоростью х0. И для точки А составляем треугольник скоростей. И в этой системе вектор ускорения шарнира будет перпендикулярен неподвижному левому звену

На неподвижном клине, образующем угол б с горизонтом, лежит груз, прикреплённый к стене перекинутой через закреплённый на клине блок нерастяжимой нитью. В некоторый момент времени клин начинает двигаться вправо с постоянной скоростью х. С какой скоростью движется груз, пока он находится на клине?

Предположим, что клин движется вправо со скоростью х. При этом надо понимать, что расстояние между точками А и В все время меняется, несмотря на то, что веревка нерастяжима. Меняется потому, что есть перегиб на блоке. Перейдем в систему отсчета, которая движется вправо со скоростью х. В этой системе клин неподвижен, а стенка уходит вправо со скоростью х. Тогда очевидно, что по неподвижному клину груз может двигаться только вдоль наклонной плоскости, то есть вдоль веревки со скоростью х. Скорость груза относительно земли, согласно классическому закону сложения скоростей равна:

В этом треугольнике скоростей ( см. рис.)

Определим результирующую скорость по теореме косинусов:

Нитку тянут со скоростью х0. Найдите угловую скорость катушки и скорость её центра. Катушка по столу и нитка по катушке не проскальзывают. Внут­ренний радиус катушки r, внешний — R.

На основании второй идеи, используя понятие мгновенного центра вращения, можно утверждать, что результирующая скорость точки А равно 0, то есть точка А — это мгновенный центр вращения. Следовательно, все остальные точки катушки проворачиваются возле точки А с одинаковой угловой скоростью, но линейная скорость у них разная, так как разный радиус вращения. Угловая скорость точки С равна:

Угловая скорость точки O равна:

Точка А, лежащая на пересечении рельса с внеш­ним ободом колеса поезда, движется в данный момент вре­мени со скоростью и =5,0 м/с (см. рис). Определить, с ка­кой скоростью и в каком направлении движется поезд, если r = 50 см, R = 56 см.

Скорость реборды u, заданная по условию, является результирующей скоростью двух скоростей: скорости поступательного движения хпоступ и линейной скорости хкасат вращательного движения вокруг точки О. Так как точка А лежит на ободе реборды, эти две скорости численно равны.

Используя вторую идею, можно считать точку С мгновенным центром вращения. Тогда скорость u будет линейной скорость точки А, вращающейся вокруг тоски С, а скорость поступательного движения так же будет линейной скоростью для точки О вращающейся вокруг точки С. И у точки А, и у точки О в этом случае будет одна и та же угловая скорость.

Следовательно, можно записать:

Кривошип ОА, вращаясь с угловой скоростью щ, приводит в движение колесо радиуса r, катящееся по неподвижному колесу радиуса R = 3r. Найдите скорость точки В.

Точка С принадлежит всем трем телам: колесу радиусом R, колесу радиусом r, и кривошипу ОА. И скорость точки А такая же, как у кривошипа, вращающегося относительно точки О с угловой скоростью щ. То есть его точка А движется с линейной скоростью, равной:

На основании второй идеи, можно считать точку С мгновенным центром вращения для колеса радиусом r. Тогда точки А и В проворачиваются относительно точки С с одинаковой угловой скоростью:

Тяжёлый диск радиуса R скатывается на двух не растяжимых нитях, намотанных на него. Свободные концы нитей закреплены. Нити при движении диска постоянно натянуты. В некоторый момент угловая скорость диска равна щ, а угол между нитями б. Какова в этот момент скорость центра диска?

Нить касается диска в точке А. Тогда, согласно третьей идеи, если одно тело катится по поверхности другого без проскальзывания, то в точках их соприкосновения и них одинаковая линейная скорость и по величине и по направлению. Величина этой скорости

Нить АА1 натянута, это значит, на основании первой идеи, что проекции скоростей точек А и А1 на нить должны быть равными. Но точка А1 неподвижна и нет у нее проекции на нить, значит не должно быть проекции и скорости в точке А. А это возможно только в том случае, если хА перпендикулярна нити.

Аналогично и для второй нити, то есть хВ перпендикулярно нити ВВ1

Значит, скорости хА и хВ направлены по радиусу диска. И после этого про нити можно забыть есть диск, две точки на нем А и В, и скорости в этих точках имеют радиальные направления.

Согласно второй идее о мгновенном центре вращения, если скорости двух точек твердого тела и эти скорости не параллельны, а образуют некоторый угол б, то мгновенный центр вращения лежит на пересечении перпендикуляров, проведенным к этим скоростям. Точка С — неподвижна, она является центром вращения, ВС и АС – радиусы окружностей, по которым вращаются соответственно точки А и В. Скорости хА и хВ перпендикулярны радиусам. В четырехугольнике угол ОАВ равен углу между нитями б как углы, образованные взаимно перпендикулярными сторонами. В этот момент скорость центра диска, то есть скорость точки О равна:

Цилиндр с намотанной на него нитью, второй конец которой закреплён, находится на горизонтальной подставке, движущейся поступательно с постоянной горизонтальной скоростью V. Найти скорость оси цилиндра в зависимости от угла б, образуемого нитью с вертикалью. Относительно подставки цилиндр не проскальзывает.

Точка С – точка соприкосновения цилиндра с подставкой. Третья идея заключается в том, что если одно тело катится по поверхности другого без проскальзывания, то в точках их соприкосновения и них одинаковая линейная скорость и по величине, и по направлению. Раз подставка движется со скоростью V. то и у точки С такая же скорость. И про доску можно забыть. То есть рассматриваем цилиндр с намотанной на него нитью. Нить касается цилиндра в точке А. В этой точке, так же как в точке С качение без проскальзывания, а это снова означает, что скорость этой точки нити равно скорости

этой точки диска. Нить не растяжима, на основании первой идеи, проекции скоростей точек А и В на нить должны быть равными. Но точка В неподвижна и нет у нее проекции на нить, значит не должно быть проекции и скорости в точке А. Это возможно только в том случае, если хА перпендикулярна нити.

Определим положение мгновенного центра вращения: он лежит на пересечении перпендикуляров ОС и ОА, проведенным к скоростям хА и хС. Мгновенным центром вращения является точка О. Ось цилиндра описывает вокруг мгновенного центра вращения окружность радиусом R1

У оси цилиндра и точки С одинаковые угловые скорости щ относительно мгновенного центра вращения.

Но точка С описывает вокруг точки О окружность радиусом (R1 +R)

Задачи для самостоятельного решения

Концы А и В стержня АВ скользят по сторонам прямого угла. Как зависит от угла б скорость х и ускорение а середины стержня, если конец В движется с постоянной скоростью. Длина стержня равна L. Нерастяжимая нить длины L соединяет две бусинки А и В. Бусинку В передвигают с посто­янной скоростью х0 по прямой спице МО. В результате этого бусинка А движется по спице CD, изогнутой в виде дуги окружности радиуса Найти ускорение бусинки А в тот момент, когда бусинка В будет на расстоянии L от точки О. Два стержня длины L соединены шарнирно. Свободный конец одного из стержней шарнирно закреплён на вертикальной стене, а свободный конец другого стержня двигают с постоянной по величине вертикальной скоростью х0. Найти величину и направление вектора ускорения шарнира, соединяющего стержни, в момент, когда их концы окажутся на одной горизонтали, если угол между стержнями в этом момент равен 2б.

Два жёстких стержня длины ℓ каждый шарнирно скреплены в точке А. жёстко закреплён в точке В, а точка С стержня АС может скользить по направляющей ВС. Стержень ВА начинают вращать в плоскости рисунка вокруг точки В с постоянной угловой скоростью щ. Чему будут равны максимальная скорость и ускорение точки С, если в начальный момент стержни вытянуты вдоль направляющей ВС (