Уравнение кинематики поступательного движения материальной точки
лЙОЕНБФЙЛБ ЙЪХЮБЕФ ТБЪМЙЮОЩЕ НЕИБОЙЮЕУЛЙЕ ДЧЙЦЕОЙС ФЕМ ВЕЪ ТБУУНПФТЕОЙС РТЙЮЙО ЧЩЪЩЧБАЭЙИ ЬФЙ ДЧЙЦЕОЙС.
1.1.1 лЙОЕНБФЙЛБ РПУФХРБФЕМШОПЗП ДЧЙЦЕОЙС
рТЙ РПУФХРБФЕМШОПН ДЧЙЦЕОЙЙ ФЕМБ ЧУЕ ФПЮЛЙ ФЕМБ ДЧЙЦХФУС ПДЙОБЛПЧП, Й, ЧНЕУФП ФПЗП ЮФПВЩ ТБУУНБФТЙЧБФШ ДЧЙЦЕОЙЕ ЛБЦДПК ФПЮЛЙ ФЕМБ, НПЦОП ТБУУНБФТЙЧБФШ ДЧЙЦЕОЙЕ ФПМШЛП ПДОПК ЕЗП ФПЮЛЙ.
пУОПЧОЩЕ ИБТБЛФЕТЙУФЙЛЙ ДЧЙЦЕОЙС НБФЕТЙБМШОПК ФПЮЛЙ: ФТБЕЛФПТЙС ДЧЙЦЕОЙС, РЕТЕНЕЭЕОЙЕ ФПЮЛЙ, РТПКДЕООЩК ЕА РХФШ, ЛППТДЙОБФЩ, УЛПТПУФШ Й ХУЛПТЕОЙЕ.
мЙОЙА, РП ЛПФПТПК ДЧЙЦЕФУС НБФЕТЙБМШОБС ФПЮЛБ Ч РТПУФТБОУФЧЕ, ОБЪЩЧБАФ ФТБЕЛФПТЙЕК.
рЕТЕНЕЭЕОЙЕН НБФЕТЙБМШОПК ФПЮЛЙ ЪБ ОЕЛПФПТЩК РТПНЕЦХФПЛ ЧТЕНЕОЙ ОБЪЩЧБЕФУС ЧЕЛФПТ РЕТЕНЕЭЕОЙС ∆r=r-r0, ОБРТБЧМЕООЩК ПФ РПМПЦЕОЙС ФПЮЛЙ Ч ОБЮБМШОЩК НПНЕОФ ЧТЕНЕОЙ Л ЕЕ РПМПЦЕОЙА Ч ЛПОЕЮОЩК НПНЕОФ.
уЛПТПУФШ НБФЕТЙБМШОПК ФПЮЛЙ РТЕДУФБЧМСЕФ УПВПК ЧЕЛФПТ, ИБТБЛФЕТЙЪХАЭЙК ОБРТБЧМЕОЙЕ Й ВЩУФТПФХ РЕТЕНЕЭЕОЙС НБФЕТЙБМШОПК ФПЮЛЙ ПФОПУЙФЕМШОП ФЕМБ ПФУЮЕФБ. чЕЛФПТ ХУЛПТЕОЙС ИБТБЛФЕТЙЪХЕФ ВЩУФТПФХ Й ОБРТБЧМЕОЙЕ ЙЪНЕОЕОЙС УЛПТПУФЙ НБФЕТЙБМШОПК ФПЮЛЙ ПФОПУЙФЕМШОП ФЕМБ ПФУЮЕФБ.
1.1.2 тБЧОПНЕТОПЕ РТСНПМЙОЕКОПЕ ДЧЙЦЕОЙЕ
тБЧОПНЕТОЩН РТСНПМЙОЕКОЩН ДЧЙЦЕОЙЕН ОБЪЩЧБЕФУС ФБЛПЕ РТСНПМЙОЕКОПЕ ДЧЙЦЕОЙЕ, РТЙ ЛПФПТПН НБФЕТЙБМШОБС ФПЮЛБ (ФЕМП) ДЧЙЦЕФУС РП РТСНПК Й Ч МАВЩЕ ТБЧОЩЕ РТПНЕЦХФЛЙ ЧТЕНЕОЙ УПЧЕТЫБЕФ ПДЙОБЛПЧЩЕ РЕТЕНЕЭЕОЙС.
чЕЛФПТ УЛПТПУФЙ ТБЧОПНЕТОПЗП РТСНПМЙОЕКОПЗП ДЧЙЦЕОЙС НБФЕТЙБМШОПК ФПЮЛЙ ОБРТБЧМЕО ЧДПМШ ЕЕ ФТБЕЛФПТЙЙ Ч УФПТПОХ ДЧЙЦЕОЙС. чЕЛФПТ УЛПТПУФЙ РТЙ ТБЧОПНЕТОПН РТСНПМЙОЕКОПН ДЧЙЦЕОЙЙ ТБЧЕО ЧЕЛФПТХ РЕТЕНЕЭЕОЙС ЪБ МАВПК РТПНЕЦХФПЛ ЧТЕНЕОЙ, РПДЕМЕООПНХ ОБ ЬФПФ РТПНЕЦХФПЛ ЧТЕНЕОЙ:
рТЙНЕН МЙОЙА, РП ЛПФПТПК ДЧЙЦЕФУС НБФЕТЙБМШОБС ФПЮЛБ, ЪБ ПУШ ЛППТДЙОБФ пи, РТЙЮЕН ЪБ РПМПЦЙФЕМШОПЕ ОБРТБЧМЕОЙЕ ПУЙ ЧЩВЕТЕН ОБРТБЧМЕОЙЕ ДЧЙЦЕОЙС ФПЮЛЙ. фПЗДБ, УРТПЕГЙТПЧБЧ ЧЕЛФПТЩ r Й v, ОБ ЬФХ ПУШ, ДМС РТПЕЛГЙК ∆rx = |∆r| Й ∆vx = |∆v| ЬФЙИ ЧЕЛФПТПЧ НЩ НПЦЕН ЪБРЙУБФШ:

ф.Л. РТЙ ТБЧОПНЕТОПН РТСНПМЙОЕКОПН ДЧЙЦЕОЙЙ S = |∆r|, НПЦЕН ЪБРЙУБФШ: Sx = vx · t. фПЗДБ ДМС ЛППТДЙОБФЩ ФЕМБ Ч МАВПК НПНЕОФ ЧТЕНЕОЙ ЙНЕЕН:
ЗДЕ И0 — ЛППТДЙОБФБ ФЕМБ Ч ОБЮБМШОЩК НПНЕОФ t = 0.
рТЙНЕТ 1. хТБЧОЕОЙЕ ДЧЙЦЕОЙС ФЕМБ ДБОП Ч ЧЙДЕ И = 4 — 3t. пРТЕДЕМЙФШ ОБЮБМШОХА ЛППТДЙОБФХ ФЕМБ, УЛПТПУФШ ДЧЙЦЕОЙС Й РЕТЕНЕЭЕОЙС ФЕМБ ЪБ 2 УЕЛХОДЩ.
тЕЫЕОЙЕ: уТБЧОЙН ДБООПЕ ХТБЧОЕОЙЕ ДЧЙЦЕОЙС ФЕМБ У ХТБЧОЕОЙЕН ДЧЙЦЕОЙС Ч ПВЭЕН ЧЙДЕ: И = И0 + vx t Й И = 4 — 3t.
пЮЕЧЙДОП, ЮФП И0 = 4Н, vx = — 3Н/У (ЪОБЛ «-» ПЪОБЮБЕФ, ЮФП ОБРТБЧМЕОЙЕ УЛПТПУФЙ ОЕ УПЧРБДБЕФ У ОБРТБЧМЕОЙЕН ПУЙ пи, Ф.Е. ПОЙ РТПФЙЧПРПМПЦОП ОБРТБЧМЕОЩ). рЕТЕНЕЭЕОЙЕ ФЕМБ ОБКДЕН РП ЖПТНХМЕ: S = И — И0. лПОЕЮОХА ЛППТДЙОБФХ И НПЦОП ПРТЕДЕМЙФШ, РПДУФБЧМСС Ч ХТБЧОЕОЙЕ ДЧЙЦЕОЙС ЧТЕНС t1: И = 4 — 3t1. ч ПВЭЕН ЧЙДЕ ЖПТНХМБ РЕТЕНЕЭЕОЙС: S = 4 — 3t1 — И0 = 4 — 3t1 — 4 = — 3t1 = -3 · 2 = — 6 Н (фЕМП ДЧЙЦЕФУС Ч ПФТЙГБФЕМШОПН ОБРТБЧМЕОЙЙ ПУЙ пи).
рТЙНЕТ 2.мПДПЮОЙЛ РЕТЕЧПЪЙФ РБУУБЦЙТПЧ У ПДОПЗП ВЕТЕЗБ ОБ ДТХЗПК ЪБ ЧТЕНС t =10 НЙО. РП ФТБЕЛФПТЙЙ бч. уЛПТПУФШ ФЕЮЕОЙС ТЕЛЙ vТ = 0,3 Н/У, ЫЙТЙОБ ТЕЛЙ 240 Н. у ЛБЛПК УЛПТПУФША v ПФОПУЙФЕМШОП ЧПДЩ Й РПД ЛБЛЙН ХЗМПН α Л ВЕТЕЗХ ДПМЦОБ ДЧЙЗБФШУС МПДЛБ, ЮФПВЩ ДПУФЙЮШ ДТХЗПЗП ВЕТЕЗБ ЪБ ХЛБЪБООПЕ ЧТЕНС?
t = 10 НЙО = 660 У.
v’ — ? α — ?

тЕЫЕОЙЕ: рТЙНЕН ВЕТЕЗ ЪБ ОЕРПДЧЙЦОХА УЙУФЕНХ ПФУЮЕФБ. фПЗДБ ПФОПУЙФЕМШОП ВЕТЕЗБ УЛПТПУФШ МПДЛЙ ТБЧОБ:
ьФБ УЛПТПУФШ (ТЙУХОПЛ 1.1), СЧМСЕФУС УХННПК ДЧХИ УЛПТПУФЕК: УЛПТПУФЙ МПДЛЙ ПФОПУЙФЕМШОП ЧПДЩ v’ (УЛПТПУФЙ ПФОПУЙФЕМШОП РПДЧЙЦОПК УЙУФЕНЩ ПФУЮЕФБ) Й УЛПТПУФЙ ТЕЛЙ vТ (УЛПТПУФЙ УБНПК РПДЧЙЦОПК УЙУФЕНЩ ПФУЮЕФБ ПФОПУЙФЕМШОП ОЕРПДЧЙЦОПК). рП ЪБЛПОХ УМПЦЕОЙС УЛПТПУФЕК: v =vТ + v’. фБЛ ЛБЛ РП ХУМПЧЙА ЪБДБЮЙ УЛПТПУФШ МПДЛЙ ПФОПУЙФЕМШОП ВЕТЕЗБ ОБРТБЧМЕОБ ЧДПМШ бч, Б УЛПТПУФШ ТЕЛЙ РЕТРЕОДЙЛХМСТОП бч, ФП УЛПТПУФШ МПДЛЙ ПФОПУЙФЕМШОП ЧПДЩ(РП ФЕПТЕНЕ рЙЖБЗПТБ):
йУЛПНЩК ХЗПМ НПЦОП ОБКФЙ ЙЪ ЧЩТБЦЕОЙС:

пФЧЕФ: v’ = 0.5 Н /У, α = arctg ≈ 53 0 .
1.1.3 оЕТБЧОПНЕТОПЕ ДЧЙЦЕОЙЕ
дЧЙЦЕОЙЕ, РТЙ ЛПФПТПН ЪБ ТБЧОЩЕ РТПНЕЦХФЛЙ ЧТЕНЕОЙ ФЕМП УПЧЕТЫБЕФ ОЕТБЧОЩЕ РЕТЕНЕЭЕОЙС ОБЪЩЧБАФ ОЕТБЧОПНЕТОЩН ЙМЙ РЕТЕНЕООЩН. уТЕДОЕК УЛПТПУФША vУТ ОБЪЩЧБЕФУС ЧЕМЙЮЙОБ, ТБЧОБС ПФОПЫЕОЙА РЕТЕНЕЭЕОЙС ФЕМБ ∆r ЪБ ОЕЛПФПТЩК РТПНЕЦХФПЛ ЧТЕНЕОЙ ∆t Л ЬФПНХ РТПНЕЦХФЛХ:
нПДХМШ УТЕДОЕК УЛПТПУФЙ ПРТЕДЕМСЕФУС ЛБЛ ПФОПЫЕОЙЕ РХФЙ ∆S, РТПКДЕООПЗП ФЕМПН ЪБ ОЕЛПФПТЩК РТПНЕЦХФПЛ ЧТЕНЕОЙ, Л ЬФПНХ РТПНЕЦХФЛХ:
оБРТБЧМЕОЙЕ ЧЕЛФПТБ УТЕДОЕК УЛПТПУФЙ vУТ УПЧРБДБЕФ У ОБРТБЧМЕОЙЕН ∆r (ТЙУХОПЛ 1.2).
рТЙ ОЕПЗТБОЙЮЕООПН ХНЕОШЫЕОЙЙ ∆t, vУТ УФТЕНЙФУС Л РТЕДЕМШОПНХ ЪОБЮЕОЙА, ЛПФПТПЕ ОБЪЩЧБЕФУС НЗОПЧЕООПК УЛПТПУФША. йФБЛ, НЗОПЧЕООБС УЛПТПУФШ v ЕУФШ РТЕДЕМ, Л ЛПФПТПНХ УФТЕНЙФУС УТЕДОСС УЛПТПУФШ vУТ, ЛПЗДБ РТПНЕЦХФПЛ ЧТЕНЕОЙ ДЧЙЦЕОЙС УФТЕНЙФУС Л ОХМА:
йЪ ЛХТУБ НБФЕНБФЙЛЙ ЙЪЧЕУФОП, ЮФП РТЕДЕМ ПФОПЫЕОЙС РТЙТБЭЕОЙС ЖХОЛГЙЙ Л РТЙТБЭЕОЙА БТЗХНЕОФБ, ЛПЗДБ РПУМЕДОЙК УФТЕНЙФУС Л ОХМА РТЕДУФБЧМСЕФ УПВПК РЕТЧХА РТПЙЪЧПДОХА ЬФПК ЖХОЛГЙЙ РП ДБООПНХ БТЗХНЕОФХ. рПЬФПНХ:
нЗОПЧЕООБС УЛПТПУФШ v ЕУФШ ЧЕЛФПТОБС ЧЕМЙЮЙОБ, ТБЧОБС РЕТЧПК РТПЙЪЧПДОПК ТБДЙХУБ — ЧЕЛФПТБ ДЧЙЦХЭЕКУС ФПЮЛЙ РП ЧТЕНЕОЙ. фБЛ ЛБЛ УЕЛХЭБС Ч РТЕДЕМЕ УПЧРБДБЕФ У ЛБУБФЕМШОПК, ФП ЧЕЛФПТ УЛПТПУФЙ v ОБРТБЧМЕО РП ЛБУБФЕМШОПК Л ФТБЕЛФПТЙЙ Ч УФПТПОХ ДЧЙЦЕОЙС (ТЙУХОПЛ 1.2).
рП НЕТЕ ХНЕОШЫЕОЙЕ ∆t РХФШ ∆S ЧУЕ ВПМШЫЕ ВХДЕФ РТЙВМЙЦБФШУС Л |∆r|, РПЬФПНХ НПДХМШ НЗОПЧЕООПК УЛПТПУФЙ:
фБЛЙН ПВТБЪПН, НПДХМШ НЗОПЧЕООПК УЛПТПУФЙ v ТБЧЕО РЕТЧПК РТПЙЪЧПДОПК РХФЙ РП ЧТЕНЕОЙ :
рТЙ ОЕТБЧОПНЕТОПН ДЧЙЦЕОЙЙ ФЕМБ ЕЗП УЛПТПУФШ ОЕРТЕТЩЧОП ЙЪНЕОСЕФУС. лБЛ ВЩУФТП ЙЪНЕОСЕФУС УЛПТПУФШ ФЕМБ, РПЛБЪЩЧБЕФ ЧЕМЙЮЙОБ, ЛПФПТБС ОБЪЩЧБЕФУС ХУЛПТЕОЙЕН. уТЕДОЙН ХУЛПТЕОЙЕН ОЕТБЧОПНЕТОПЗП ДЧЙЦЕОЙС Ч ЙОФЕТЧБМЕ ПФ t ДП t + ∆t ОБЪЩЧБЕФУС ЧЕЛФПТОБС ЧЕМЙЮЙОБ, ТБЧОБС ПФОПЫЕОЙА ЙЪНЕОЕОЙС УЛПТПУФЙ ∆v Л ЙОФЕТЧБМХ ЧТЕНЕОЙ ∆t:
нЗОПЧЕООЩН ХУЛПТЕОЙЕН Б Ч НПНЕОФ ЧТЕНЕОЙ t ВХДЕФ РТЕДЕМ УТЕДОЕЗП ХУЛПТЕОЙС:
фБЛЙН ПВТБЪПН, ХУЛПТЕОЙЕ ∆Б ЕУФШ ЧЕЛФПТОБС ЧЕМЙЮЙОБ, ТБЧОБС РЕТЧПК РТПЙЪЧПДОПК УЛПТПУФЙ РП ЧТЕНЕОЙ. ч ДБООПК УЙУФЕНЕ ПФУЮЕФБ ЧЕЛФПТ ХУЛПТЕОЙС НПЦЕФ ВЩФШ ЪБДБО РТПЕЛГЙСНЙ ОБ УППФЧЕФУФЧХАЭЙЕ ЛППТДЙОБФОЩЕ ПУЙ (РТПЕЛГЙСНЙ БИ, БХ, Бz).
уПУФБЧМСАЭБС Бτ ЧЕЛФПТБ ХУЛПТЕОЙС, ОБРТБЧМЕООБС ЧДПМШ ЛБУБФЕМШОПК Л ФТБЕЛФПТЙЙ Ч ДБООПК ФПЮЛЕ, ОБЪЩЧБЕФУС ФБОЗЕОГЙБМШОЩН (ЛБУБФЕМШОЩН) ХУЛПТЕОЙЕН. фБОЗЕОГЙБМШОПЕ ХУЛПТЕОЙЕ ИБТБЛФЕТЙЪХЕФ ЙЪНЕОЕОЙЕ ЧЕЛФПТБ УЛПТПУФЙ РП НПДХМА. чЕЛФПТ Бτ ОБРТБЧМЕО Ч УФПТПОХ ДЧЙЦЕОЙС ФПЮЛЙ РТЙ ЧПЪТБУФБОЙЙ ЕЕ УЛПТПУФЙ (ТЙУХОПЛ 1.3 — Б) Й Ч РТПФЙЧПРПМПЦОХА УФПТПОХ — РТЙ ХВЩЧБОЙЙ УЛПТПУФЙ (ТЙУХОПЛ 1.3 — В).
 Б) |  В) | ||||||
 тЕЫЕОЙЕ: рХУФШ ПУШ пи УПЧРБДБЕФ У ОБРТБЧМЕОЙЕН ДЧЙЦЕОЙС РЕТЧПЗП ЧЕМПУЙРЕДЙУФБ, Б ОБЮБМП ЛППТДЙОБФ У ФПЮЛПК O, Ч ЛПФПТПК ПО ОБИПДЙМУС Ч НПНЕОФ ЧТЕНЕОЙ t = 0 (ТЙУХОПЛ 1.4). фПЗДБ ХТБЧОЕОЙС ДЧЙЦЕОЙС ЧЕМПУЙРЕДЙУФБ ФБЛПЧЩ : ч НПНЕОФ ЧУФТЕЮЙ Ч ФПЮЛЕ б: t = t1; x1 = x2. фПЗДБ РПМХЮЙН ТБЧЕОУФЧП:
пРТЕДЕМЙН РЕТЕНЕЭЕОЙЕ ЛБЦДПЗП ДП ЧУФТЕЮЙ. 1.1.5 уЧПВПДОПЕ РБДЕОЙЕ ФЕМ. дЧЙЦЕОЙЕ ФЕМБ, ВТПЫЕООПЗП ЧЕТФЙЛБМШОП ЧЧЕТИуЧПВПДОЩН РБДЕОЙЕН ОБЪЩЧБЕФУС ДЧЙЦЕОЙЕ, ЛПФПТПЕ УПЧЕТЫЙМП ВЩ ФЕМП ФПМШЛП РПД ДЕКУФЧЙЕН УЙМЩ ФСЦЕУФЙ ВЕЪ ХЮЕФБ УПРТПФЙЧМЕОЙС ЧПЪДХИБ. рТЙ УЧПВПДОПН РБДЕОЙЙ ФЕМБ У ОЕВПМШЫПК ЧЩУПФЩ h ПФ РПЧЕТИОПУФЙ ъЕНМЙ (h ≪RЪ, ЗДЕ RЪ — ТБДЙХУ ъЕНМЙ) ПОП ДЧЙЦЕФУС У РПУФПСООЩН ХУЛПТЕОЙЕН g, ОБРТБЧМЕООЩН ЧЕТФЙЛБМШОП ЧОЙЪ. хУЛПТЕОЙЕ g ОБЪЩЧБЕФУС ХУЛПТЕОЙЕН УЧПВПДОПЗП РБДЕОЙС. пОП ПДОП Й ФПЦЕ ДМС ЧУЕИ ФЕМ Й ЪБЧЙУЙФ МЙЫШ ПФ ЧЩУПФЩ ОБД ХТПЧОЕН НПТС Й ПФ ЗЕПЗТБЖЙЮЕУЛПК ЫЙТПФЩ. еУМЙ Ч НПНЕОФ ОБЮБМБ ПФУЮЕФБ ЧТЕНЕОЙ (t0 = 0) ФЕМП ЙНЕМП УЛПТПУФШ v0, ФП РП ЙУФЕЮЕОЙЙ РТПЙЪЧПМШОПЗП РТПНЕЦХФЛБ ЧТЕНЕОЙ ∆t = t — t0 УЛПТПУФШ ФЕМБ РТЙ УЧПВПДОПН РБДЕОЙЙ ВХДЕФ: v = v0 + g·t. рХФШ h, РТПКДЕООЩК ФЕМПН Ч УЧПВПДОПН РБДЕОЙЙ, Л НПНЕОФХ ЧТЕНЕОЙ t: нПДХМШ УЛПТПУФЙ ФЕМБ РПУМЕ РТПИПЦДЕОЙС Ч УЧПВПДОПН РБДЕОЙЙ РХФЙ h ОБИПДЙФУС ЙЪ ЖПТНХМЩ: рТПДПМЦЙФЕМШОПУФШ ∆t УЧПВПДОПЗП РБДЕОЙС ВЕЪ ОБЮБМШОПК УЛПТПУФЙ (v0 = 0) У ЧЩУПФЩ h: рТЙНЕТ 1. фЕМП РБДБЕФ ЧЕТФЙЛБМШОП ЧОЙЪ У ЧЩУПФЩ 20 Н ВЕЪ ОБЮБМШОПК УЛПТПУФЙ. пРТЕДЕМЙФШ: 1) РХФШ h, РТПКДЕООЩК ФЕМПН ЪБ РПУМЕДОАА УЕЛХОДХ РБДЕОЙС, 2) УТЕДОАА УЛПТПУФШ РБДЕОЙС vУТ, 3) УТЕДОАА УЛПТПУФШ ОБ ЧФПТПК РПМПЧЙОЕ РХФЙ vУТ2. |  тЕЫЕОЙЕ: оБРТБЧЙН ПУШ Х ЧЕТФЙЛБМШОП ЧОЙЪ, Й РХУФШ ОБЮБМП ЛППТДЙОБФ УПЧРБДБЕФ У ОБЮБМШОЩН РПМПЦЕОЙЕН ФЕМБ (ТЙУХОПЛ 1.5). 1) уПЗМБУОП ЖПТНХМЕ: ХТБЧОЕОЙЕ ДЧЙЦЕОЙС ЪБРЙЫЕФУС Ч ЧЙДЕ: Ч НПНЕОФ РБДЕОЙС ОБ ЪЕНМА Х = h0. пФУАДБ ЧТЕНС ДЧЙЦЕОЙС ФЕМБ: ъБ ЧТЕНС ( t — ∆t) ФЕМП РТПЫМП РХФШ рХФШ ЪБ РПУМЕДОАА УЕЛХОДХ ТБЧЕО: 2) фЕМП РТПЫМП РХФШ h0. чТЕНС ДЧЙЦЕОЙС
3) дМС ПРТЕДЕМЕОЙС УТЕДОЕК УЛПТПУФЙ ОБ ЧФПТПК РПМПЧЙОЕ РХФЙ, ОЕПВИПДЙНП ХЪОБФШ ЧТЕНС, ЪБ ЛПФПТПЕ ЬФБ ЮБУФШ РХФЙ РТПКДЕОБ. чТЕНС ДЧЙЦЕОЙС ОБ ЧФПТПК РПМПЧЙОЕ РХФЙ ТБЧОП РПМОПНХ ЧТЕНЕОЙ РПМЕФБ t НЙОХУ ЧТЕНС t1, ЪБФТБЮЕООПЕ ОБ РТПИПЦДЕОЙЕ РЕТЧПК РПМПЧЙОЩ РХФЙ. чТЕНС t1 ОБИПДЙФУС ЙЪ ХТБЧОЕОЙС: | ,Ф.Е. |  |
 |
 |
рТЙ ДЧЙЦЕОЙЙ ФЕМБ ЧЕТФЙЛБМШОП ЧЧЕТИ У ОБЮБМШОПК УЛПТПУФША v0, ХУЛПТЕОЙЕ ФЕМБ ТБЧОП ХУЛПТЕОЙА УЧПВПДОПЗП РБДЕОЙС g. оБ ХЮБУФЛЕ ДП ОБЙЧЩУЫЕК ФПЮЛЙ РПДЯЕНБ ДЧЙЦЕОЙЕ ФЕМБ СЧМСЕФУС ТБЧОПЪБНЕДМЕООЩН, Б РПУМЕ ДПУФЙЦЕОЙС ЬФПК ФПЮЛЙ — УЧПВПДОЩН РБДЕОЙЕН ВЕЪ ОБЮБМШОПК УЛПТПУФЙ.
уЛПТПУФШ ФЕМБ Ч РТПЙЪЧПМШОЩК НПНЕОФ ЧТЕНЕОЙ t ПФ ОБЮБМБ ДЧЙЦЕОЙС ОЕЪБЧЙУЙНП ПФ ФПЗП, ТБУУНБФТЙЧБЕФУС МЙЫШ РПДЯЕН ФЕМБ ЙМЙ ЕЗП ПРХУЛБОЙЕ РПУМЕ ДПУФЙЦЕОЙС ОБЙЧЩУЫЕК ФПЮЛЙ, ТБЧОБ v = v0 + g·t.
чЕЛФПТ РЕТЕНЕЭЕОЙС ∆r ФЕМБ ЪБ РТПЙЪЧПМШОЩК РТПНЕЦХФПЛ ЧТЕНЕОЙ ∆t = t — t0, РТЙ ХУМПЧЙЙ t0 = 0, ТБЧЕО:
ч НПНЕОФ ЧТЕНЕОЙ tРПД, УППФЧЕФУФЧХАЭЙК ОБЙВПМШЫЕНХ РПДЯЕНХ ФЕМБ ОБД ФПЮЛПК ВТПУБОЙС (ЛПЗДБ Х = ХНБИ ЙМЙ ЧЩУПФБ РПДЯЕНБ ФЕМБ НБЛУЙНБМШОБ h = hmax = Хmax — Х0) УЛПТПУФШ ФЕМБ УФБОЕФ ТБЧОБ ОХМА: v = v0 — g·tРПД = 0, ПФЛХДБ tРПД = v0/g, Ч ЬФПФ НПНЕОФ ОБРТБЧМЕОЙЕ ДЧЙЦЕОЙС ФЕМБ ЙЪНЕОСЕФУС ОБ РТПФЙЧПРПМПЦОПЕ.
нБЛУЙНБМШОБС ЧЩУПФБ РПДЯЕНБ ФЕМБ ОБД ФПЮЛПК ВТПУБОЙС:
1.1.6 дЧЙЦЕОЙЕ ФЕМБ, ВТПЫЕООПЗП РПД ХЗМПН Л ЗПТЙЪПОФХ Й ВТПЫЕООПЗП ЗПТЙЪПОФБМШОП У ОЕЛПФПТПК ЧЩУПФЩ
дЧЙЦЕОЙЕ ФЕМБ, ВТПЫЕООПЗП У ОЕЛПФПТПК ЧЩУПФЩ, НПЦОП ТБЪМПЦЙФШ ОБ ДЧБ ОЕЪБЧЙУЙНЩИ ДЧЙЦЕОЙС: ТБЧОПНЕТОПЕ РТСНПМЙОЕКОПЕ, РТПЙУИПДСЭЕЕ Ч ЗПТЙЪПОФБМШОПН ОБРТБЧМЕОЙЙ УП УЛПТПУФША υИ , ТБЧОПК ОБЮБМШОПК УЛПТПУФЙ ВТПУБОЙС υ0 (υИ = υ0), Й УЧПВПДОПЕ РБДЕОЙЕ У ЧЩУПФЩ, ОБ ЛПФПТПК ОБИПДЙМПУШ ФЕМП Ч НПНЕОФ ВТПУБОЙС, У ХУЛПТЕОЙЕН g. дМС ПРЙУБОЙС ЬФПЗП ДЧЙЦЕОЙС ЧЩВЙТБАФ РТСНПХЗПМШОХА УЙУФЕНХ ЛППТДЙОБФ ИпХ. фТБЕЛФПТЙС ДЧЙЦЕОЙС СЧМСЕФУС ЧЕФЧШ РБТБВПМЩ (ТЙУХОПЛ 1.6).
хТБЧОЕОЙЕ ДЧЙЦЕОЙС РП ПУСН пИ Й пХ:
уЛПТПУФШ ФЕМБ Ч МАВПК ФПЮЛЕ ФТБЕЛФПТЙЙ НПЦОП ПРТЕДЕМЙФШ РП ЖПТНХМЕ:
рТЙ ЬФПН ЧТЕНС РПМЕФБ УЧСЪБОП У ЧЕТФЙЛБМШОПК УПУФБЧМСАЭЕК ДЧЙЦЕОЙС. дБМШОПУФШ РПМЕФБ — У ЗПТЙЪПОФБМШОПК.
рТЙНЕТ 1. у ВБЫОЙ ЧЩУПФПК о = 25 Н ЗПТЙЪПОФБМШОП ВТПЫЕО ЛБНЕОШ УП УЛПТПУФША υ0 = 15 Н/У. оБКФЙ: УЛПМШЛП ЧТЕНЕОЙ ЛБНЕОШ ВХДЕФ Ч ДЧЙЦЕОЙЙ; ОБ ЛБЛПН ТБУУФПСОЙЙ Sx ПФ ПУОПЧБОЙЙ ВБЫОЙ ПО ХРБДЕФ ОБ ЪЕНМА; У ЛБЛПК УЛПТПУФША υ ПО ХРБДЕФ ОБ ЪЕНМА; ЛБЛПК ХЗПМ φ УПУФБЧЙФ ФТБЕЛФПТЙС ЛБНОС У ЗПТЙЪПОФПН Ч ФПЮЛЕ ЕЗП РБДЕОЙС ОБ ЪЕНМА.
рЕТЕНЕЭЕОЙЕ ВТПЫЕООПЗП ЗПТЙЪПОФБМШОП ЛБНОС НПЦОП ТБЪМПЦЙФШ ОБ ДЧБ (ТЙУХОПЛ 1.7): ЗПТЙЪПОФБМШОПЕ Sx Й ЧЕТФЙЛБМШОПЕ Sy.
рТЙНЕОСС ЪБЛПО ОЕЪБЧЙУЙНПУФЙ ДЧЙЦЕОЙС, ЙНЕЕН:


1)

2) Sx = L = v0·t = 15 · 2,26 = 33,9 Н;
3) vХ = g · t = 9,81 · 2,26 = 22,1 Н/У,
4)

дЧЙЦЕОЙЕ ФЕМБ, ВТПЫЕООПЗП РПД ХЗМПН Л ЗПТЙЪПОФХ, ФБЛЦЕ НПЦОП ТБЪМПЦЙФШ ОБ ДЧБ ОЕЪБЧЙУЙНЩИ ДЧЙЦЕОЙС: ТБЧОПНЕТОПЕ РТСНПМЙОЕКОПЕ, РТПЙУИПДСЭЕЕ Ч ЗПТЙЪПОФБМШОПН ОБРТБЧМЕОЙЙ У ОБЮБМШОПК УЛПТПУФША v0И = v0·Cosα Й УЧПВПДОПЕ РБДЕОЙЕ У ОБЮБМШОПК УЛПТПУФША v0Х = v0·Sinα, (ТЙУХОПЛ 1.8). зДЕ α — ХЗПМ НЕЦДХ ОБРТБЧМЕОЙСНЙ ЧЕЛФПТБ УЛПТПУФЙ υ0 Й ПУША пИ. фТБЕЛФПТЙЕК ФБЛПЗП ДЧЙЦЕОЙС СЧМСЕФУС РБТБВПМБ. хТБЧОЕОЙС ДЧЙЦЕОЙС РТЙНХФ ЧЙД:
уЛПТПУФШ ФЕМБ Ч МАВПК ФПЮЛЕ ФТБЕЛФПТЙЙ:
рТЙНЕТ 2. фЕМП ВТПЫЕОП РПД ХЗМПН α Л ЗПТЙЪПОФХ У ОБЮБМШОПК УЛПТПУФША υ0. пРТЕДЕМЙФШ ЧТЕНС РПМЕФБ t, НБЛУЙНБМШОХА ЧЩУПФХ о РПДЯЕНБ Й ДБМШОПУФШ L РПМЕФБ.
тЕЫЕОЙЕ: лБЛ ПВЩЮОП ЪБДБЮБ ОБЮЙОБЕФУС У ЧЩСЧМЕОЙС УЙМ, ДЕКУФЧХАЭЙИ ОБ ФЕМП. оБ ФЕМП ДЕКУФЧХЕФ ФПМШЛП УЙМБ ФСЦЕУФЙ, РПЬФПНХ Ч ЗПТЙЪПОФБМШОПН ОБРТБЧМЕОЙЙ ПОП РЕТЕНЕЭБЕФУС ТБЧОПНЕТОП, Б Ч ЧЕТФЙЛБМШОПН — ТБЧОПРЕТЕНЕООП У ХУЛПТЕОЙЕН g.
вХДЕН ТБУУНБФТЙЧБФШ ЧЕТФЙЛБМШОХА Й ЗПТЙЪПОФБМШОХА УПУФБЧМСАЭЙЕ ДЧЙЦЕОЙС ФЕМБ РП ПФДЕМШОПУФЙ, ДМС ЬФПЗП ТБЪМПЦЙН ЧЕЛФПТ ОБЮБМШОПК УЛПТПУФЙ ОБ ЧЕТФЙЛБМШОХА ( υ0·Sinα ) Й ЗПТЙЪПОФБМШОХА ( υ0·Cosα ) УПУФБЧМСАЭЙЕ (ТЙУХОПЛ 1.9).
оБЮОЕН ТБУУНБФТЙЧБФШ ЧЕТФЙЛБМШОХА УПУФБЧМСАЭХА ДЧЙЦЕОЙС. чТЕНС РПМЕФБ t = t1 + t2, ЗДЕ t1 — ЧТЕНС РПДЯЕНБ (ФЕМП ДЧЙЦЕФУС РП ЧЕТФЙЛБМЙ ТБЧОПЪБНЕДМЕООП), t2 — ЧТЕНС УРХУЛБ (ФЕМП ДЧЙЦЕФУС РП ЧЕТФЙЛБМЙ ТБЧОПХУЛПТЕООП).
чЕТФЙЛБМШОБС УЛПТПУФШ ФЕМБ Ч ОБЙЧЩУЫЕК ФПЮЛЕ ФТБЕЛФПТЙЙ (РТЙ t = t1) ТБЧОБ ПЮЕЧЙДОП ОХМА. у ДТХЗПК УФПТПОЩ, ЬФБ УЛПТПУФШ НПЦЕФ ВЩФШ ЧЩТБЦЕОБ РТЙ РПНПЭЙ ЖПТНХМЩ ЪБЧЙУЙНПУФЙ УЛПТПУФЙ ТБЧОПЪБНЕДМЕООПЗП ДЧЙЦЕОЙС ПФ ЧТЕНЕОЙ.
пФУАДБ, РПМХЮБЕН: 0 = υ0Sinα — g·t1 ЙМЙ
рПДУФБЧЙН (1.1) Ч (1.2)
чТЕНС УРХУЛБ t2 НПЦОП ЧЩЮЙУМЙФШ, ТБУУНПФТЕЧ РБДЕОЙЕ ФЕМБ У ЙЪЧЕУФОПК ЧЩУПФЩ о ВЕЪ ОБЮБМШОПК ЧЕТФЙЛБМШОПК УЛПТПУФЙ:
рПМОПЕ ЧТЕНС РПМЕФБ:
дМС ОБИПЦДЕОЙС ДБМШОПУФЙ РПМЕФБ L ОЕПВИПДЙНП ПВТБФЙФШУС Л ЗПТЙЪПОФБМШОПК УПУФБЧМСАЭЕК ДЧЙЦЕОЙС ФЕМБ. лБЛ ХЦЕ ПФНЕЮБМПУШ, РП ЗПТЙЪПОФБМЙ ФЕМП РЕТЕНЕЭБЕФУС ТБЧОПНЕТОП.
1.1.7 тБЧОПРЕТЕНЕООПЕ ДЧЙЦЕОЙЕ ФПЮЛЙ РП ПЛТХЦОПУФЙ
дЧЙЦЕОЙЕ РП ПЛТХЦОПУФЙ СЧМСЕФУС РТПУФЕКЫЙН РТЙНЕТПН ЛТЙЧПМЙОЕКОПЗП ДЧЙЦЕОЙС. уЛПТПУФШ υ ДЧЙЦЕОЙС РП ПЛТХЦОПУФЙ ОБЪЩЧБЕФУС МЙОЕКОПК (ПЛТХЦОПК) УЛПТПУФША. рТЙ ТБЧОПНЕТОПН ДЧЙЦЕОЙЙ РП ПЛТХЦОПУФЙ НПДХМШ НЗОПЧЕООПК УЛПТПУФЙ НБФЕТЙБМШОПК ФПЮЛЙ У ФЕЮЕОЙЕН ЧТЕНЕОЙ ОЕ ЙЪНЕОСЕФУС. дЧЙЦХЭБСУС ФПЮЛБ ЪБ ТБЧОЩЕ РТПНЕЦХФЛЙ ЧТЕНЕОЙ РТПИПДЙФ ТБЧОЩЕ РП ДМЙОЕ ДХЗЙ ПЛТХЦОПУФЙ. фБОЗЕОГЙБМШОПЕ ХУЛПТЕОЙЕ РТЙ ТБЧОПНЕТОПН ДЧЙЦЕОЙЙ ФПЮЛЙ РП ПЛТХЦОПУФЙ ПФУХФУФЧХЕФ ( aτ ). йЪНЕОЕОЙЕ ЧЕЛФПТБ УЛПТПУФЙ υ РП ОБРТБЧМЕОЙА ИБТБЛФЕТЙЪХЕФУС ОПТНБМШОЩН ХУЛПТЕОЙЕН an, ЛПФПТПЕ ОБЪЩЧБЕФУС ФБЛЦЕ ГЕОФТПУФТЕНЙФЕМШОЩН ХУЛПТЕОЙЕН.
ч ЛБЦДПК ФПЮЛЕ ФТБЕЛФПТЙЙ ЧЕЛФПТ an ОБРТБЧМЕО РП ТБДЙХУХ Л ГЕОФТХ ПЛТХЦОПУФЙ, Б ЕЗП НПДХМШ ТБЧЕО:
рТЙ ПРЙУБОЙЙ НЕИБОЙЮЕУЛПЗП ДЧЙЦЕОЙС, Ч ЮБУФОПУФЙ ДЧЙЦЕОЙС РП ПЛТХЦОПУФЙ, ОБТСДХ У РТСНПХЗПМШОПК ДЕЛБТФПЧПК УЙУФЕНПК ЛППТДЙОБФ ЙУРПМШЪХЕФУС РПМСТОБС УЙУФЕНБ ЛППТДЙОБФ. рПМПЦЕОЙЕ ФПЮЛЙ н ОБ ЛБЛПК-ФП РМПУЛПУФЙ (ОБРТЙНЕТ, ипх) ПРТЕДЕМСЕФУС ДЧХНС РПМСТОЩНЙ ЛППТДЙОБФБНЙ: НПДХМЕН r ТБДЙХУБ ЧЕЛФПТБ ФПЮЛЙ Й ХЗМПН φ — ХЗМПЧПК ЛППТДЙОБФПК, ЙМЙ РПМСТОЩН ХЗМПН (ТЙУХОПЛ 1.10).
хЗПМ φ ПФУЮЙФЩЧБЕФУС ПФ ПУЙ пи ДП ТБДЙХУБ-ЧЕЛФПТБ r РТПФЙЧ ЮБУПЧПК УФТЕМЛЙ. фПЮЛХ п Ч ЬФПН УМХЮБЕ ОБЪЩЧБАФ РПМАУПН УЙУФЕНЩ ЛППТДЙОБФ. уПЧНЕУФЙН РПМАУ ЛППТДЙОБФ УЙУФЕНЩ У ГЕОФТПН ПЛТХЦОПУФЙ, РП ЛПФПТПК ДЧЙЦЕФУС НБФЕТЙБМШОБС ФПЮЛБ; ФПЗДБ r = R (ТЙУХОПЛ 1.11), Б ЙЪНЕОЕОЙЕ РПМПЦЕОЙС ФПЮЛЙ ОБ ПЛТХЦОПУФЙ НПЦЕФ ВЩФШ ПИБТБЛФЕТЙЪПЧБОП ЙЪНЕОЕОЙЕН ∆φ ХЗМПЧПК ЛППТДЙОБФЩ ФПЮЛЙ: ∆φ = φ2 -φ1.
хЗПМ ∆φ ОБЪЩЧБЕФУС ХЗМПН РПЧПТПФБ ТБДЙХУБ — ЧЕЛФПТБ ФПЮЛЙ. ьМЕНЕОФБТОЩЕ (ВЕУЛПОЕЮОП НБМЩЕ) ХЗМЩ РПЧПТПФБ ТБУУНБФТЙЧБАФУС ЛБЛ ЧЕЛФПТЩ.
нПДХМШ ЧЕЛФПТБ dφ ТБЧЕО ХЗМХ РПЧПТПФБ. оБРТБЧМЕОЙЕ ЧЕЛФПТБ dφ УПЧРБДБЕФ У ОБРТБЧМЕОЙЕН РПУФХРБФЕМШОПЗП ДЧЙЦЕОЙС ПУФТЙС ЧЙОФБ, ЗПМПЧЛБ ЛПФПТПЗП, ЧТБЭБЕФУС Ч ОБРТБЧМЕОЙЙ ДЧЙЦЕОЙС ФПЮЛЙ РП ПЛТХЦОПУФЙ, Ф.Е. РПДЮЙОСЕФУС РТБЧЙМХ РТБЧПЗП ЧЙОФБ (ТЙУХОПЛ 1.12).
CТЕДОЕК ХЗМПЧПК УЛПТПУФША ДЧЙЦЕОЙС ФПЮЛЙ РП ПЛТХЦОПУФЙ ЧПЛТХЗ ПУЙ ОБЪЩЧБЕФУС ЧЕМЙЮЙОБ ωcp, ТБЧОБС ПФОПЫЕОЙА ХЗМБ РПЧПТПФБ ∆φ ТБДЙХУ-ЧЕЛФПТБ ФПЮЛЙ ЪБ РТПНЕЦХФПЛ ЧТЕНЕОЙ ∆t Л ДМЙФЕМШОПУФЙ ЬФПЗП РТПНЕЦХФЛБ:
хЗМПЧПК УЛПТПУФША (НЗОПЧЕООПК ХЗМПЧПК УЛПТПУФША) ω ОБЪЩЧБЕФУС РТЕДЕМ, Л ЛПФПТПНХ УФТЕНЙФУС УТЕДОСС ХЗМПЧБС УЛПТПУФШ РТЙ ВЕУЛПОЕЮОПН ХНЕОШЫЕОЙЙ РТПНЕЦХФЛБ ЧТЕНЕОЙ ∆t, ЙМЙ РЕТЧБС РТПЙЪЧПДОБС ПФ ХЗМБ РПЧПТПФБ РП ЧТЕНЕОЙ:
чЕЛФПТ ω ОБРТБЧМЕО ЧДПМШ ПУЙ ЧТБЭЕОЙС РП РТБЧЙМХ РТБЧПЗП ЧЙОФБ, Ф.Е. ФБЛЦЕ ЛБЛ Й dφ (ТЙУХОПЛ 1.13).
рТЙ ТБЧОПНЕТОПН ДЧЙЦЕОЙЙ ФПЮЛЙ РП ПЛТХЦОПУФЙ ЪБ МАВЩЕ ТБЧОЩЕ РТПНЕЦХФЛЙ ЧТЕНЕОЙ ХЗМЩ РПЧПТПФБ ЕЕ ТБДЙХУ-ЧЕЛФПТБ ПДЙОБЛПЧЩ. уМЕДПЧБФЕМШОП, РТЙ ФБЛПН ДЧЙЦЕОЙЙ НЗОПЧЕООБС ХЗМПЧБС УЛПТПУФШ ТБЧОБ УТЕДОЕК ХЗМПЧПК УЛПТПУФЙ: ω = ωcp. хЗПМ РПЧПТПФБ ∆ω ТБДЙХУ-ЧЕЛФПТБ ФПЮЛЙ, ТБЧОПНЕТОП ДЧЙЦХЭЕКУС РП ПЛТХЦОПУФЙ, ТБЧЕО:
рТПНЕЦХФПЛ ЧТЕНЕОЙ ф, Ч ФЕЮЕОЙЙ ЛПФПТПЗП ФПЮЛБ УПЧЕТЫБЕФ ПДЙО РПМОЩК ПВПТПФ РП ПЛТХЦОПУФЙ, ОБЪЩЧБЕФУС РЕТЙПДПН ПВТБЭЕОЙС (РЕТЙПДПН ЧТБЭЕОЙС), Б ЧЕМЙЮЙОБ υ, ПВТБФОБС РЕТЙПДХ:

ЮБУФПФПК ПВТБЭЕОЙС (ЮБУФПФПК ЧТБЭЕОЙС). ъБ ПДЙО РЕТЙПД ХЗПМ РПЧПТПФБ ТБДЙХУ-ЧЕЛФПТБ ФПЮЛЙ ТБЧЕО 2π ТБД, РПЬФПНХ 2π = ωT, ПФЛХДБ T = 2π/ω, ЙМЙ ω = 2π/ф = 2πν.
мЙОЕКОБС υ Й ХЗМПЧБС ω УЛПТПУФЙ УЧСЪБОЩ УППФОПЫЕОЙЕН: υ = ω·R. ьФП ЧЙДОП ЙЪ УМЕДХАЭЕЗП ЧЩЧПДБ:
рТЙНЕТ 1. пРТЕДЕМЙФШ НПДХМШ УЛПТПУФЙ Й ГЕОФТПУФТЕНЙФЕМШОПЗП ХУЛПТЕОЙС ФПЮЕЛ ЪЕНОПК РПЧЕТИОПУФЙ ОБ ЬЛЧБФПТЕ. тБДЙХУ ъЕНМЙ РТЙОСФШ ТБЧОЩН 6400 ЛН.
R = 6400 ЛН = 6,4·10 6 Н;
ф = 24 Ю = 8,64·10 4 У;
тЕЫЕОЙЕ: фПЮЛЙ ЪЕНОПК РПЧЕТИОПУФЙ ОБ ЬЛЧБФПТЕ ДЧЙЦХФУС РП ПЛТХЦОПУФЙ ТБДЙХУБ R, РПЬФПНХ НПДХМШ ЙИ УЛПТПУФЙ:
пФЧЕФ: υ = 465 Н/У, БГУ = 0,034 Н /У 2 .
1.1.8 чТБЭБФЕМШОПЕ ДЧЙЦЕОЙЕ БВУПМАФОП ФЧЕТДПЗП ФЕМБ ЧПЛТХЗ ОЕРПДЧЙЦОПК ПУЙ
дМС ЛЙОЕНБФЙЮЕУЛПЗП ПРЙУБОЙС ЧТБЭБФЕМШОПЗП ДЧЙЦЕОЙС БВУПМАФОП ФЧЕТДПЗП ФЕМБ ЧПЛТХЗ ЛБЛПК-ФП ОЕРПДЧЙЦОПК ПУЙ ЙУРПМШЪХАФУС ФЕ ЦЕ ЧЕМЙЮЙОЩ (Й ХТБЧОЕОЙС УЧСЪЙ НЕЦДХ ОЙНЙ), ЮФП Й ДМС ПРЙУБОЙС ДЧЙЦЕОЙС ФПЮЛЙ РП ПЛТХЦОПУФЙ. рТЙ ЧТБЭБФЕМШОПН ДЧЙЦЕОЙЙ БВУПМАФОП ФЧЕТДПЗП ФЕМБ ЧПЛТХЗ ОЕРПДЧЙЦОПК ПУЙ ЪБ РТПНЕЦХФПЛ ЧТЕНЕОЙ ∆t ХЗМЩ РПЧПТПФБ ТБДЙХУ-ЧЕЛФПТПЧ ТБЪМЙЮОЩИ ФПЮЕЛ ФЕМБ ПДЙОБЛПЧЩ. хЗПМ РПЧПТПФБ ∆φ, УТЕДОСС ωcp Й НЗОПЧЕООБС ω ХЗМПЧЩЕ УЛПТПУФЙ ИБТБЛФЕТЙЪХАФ ЧТБЭБФЕМШОПЕ ДЧЙЦЕОЙЕ ЧУЕЗП БВУПМАФОП ФЧЕТДПЗП ФЕМБ Ч ГЕМПН.
мЙОЕКОБС УЛПТПУФШ υ ЛБЛПК-МЙВП ФПЮЛЙ БВУПМАФОП ФЧЕТДПЗП ФЕМБ РТПРПТГЙПОБМШОП ТБУУФПСОЙА R ФПЮЛЙ ПФ ПУЙ ЧТБЭЕОЙС:
рТЙ ТБЧОПНЕТОПН ЧТБЭБФЕМШОПН ДЧЙЦЕОЙЙ БВУПМАФОП ФЧЕТДПЗП ФЕМБ ХЗМЩ РПЧПТПФБ ФЕМБ ЪБ МАВЩЕ ТБЧОЩЕ РТПНЕЦХФЛЙ ЧТЕНЕОЙ ПДЙОБЛПЧЩ ( ∆φ = const ) Й НЗОПЧЕООБС ХЗМПЧБС УЛПТПУФШ ФЕМБ ТБЧОБ УТЕДОЕК ХЗМПЧПК УЛПТПУФЙ ( ω = ωcp ). фБОЗЕОГЙБМШОЩЕ ХУЛПТЕОЙС aτ Х ТБЪМЙЮОЩИ ФПЮЕЛ БВУПМАФОП ФЧЕТДПЗП ФЕМБ ПФУХФУФЧХАФ ( aτ = 0 ), Б ОПТНБМШОПЕ (ГЕОФТПУФТЕНЙФЕМШОПЕ ) ХУЛПТЕОЙЕ an ЛБЛПК-МЙВП ФПЮЛЙ ФЕМБ ЪБЧЙУЙФ ПФ ЕЕ ТБУУФПСОЙС R ДП ПУЙ ЧТБЭЕОЙС:
чЕЛФПТ an ОБРТБЧМЕО Ч ЛБЦДЩК НПНЕОФ ЧТЕНЕОЙ РП ТБДЙХУХ ФТБЕЛФПТЙЙ ФПЮЛЙ Л ПУЙ ЧТБЭЕОЙС.
рТЙ ОЕТБЧОПНЕТОПН ЧТБЭБФЕМШОПН ДЧЙЦЕОЙЙ БВУПМАФОП ФЧЕТДПЗП ФЕМБ ХЗМЩ РПЧПТПФБ ФЕМБ ЪБ МАВЩЕ ТБЧОЩЕ РТПНЕЦХФЛЙ ЧТЕНЕОЙ ОЕПДЙОБЛПЧЩ. хЗМПЧБС УЛПТПУФШ ФЕМБ ω У ФЕЮЕОЙЕН ЧТЕНЕОЙ ЙЪНЕОСЕФУС.
уТЕДОЙН ХЗМПЧЩН ХУЛПТЕОЙЕН εУТ Ч РТПНЕЦХФЛЕ ЧТЕНЕОЙ ∆t = t2 — t1 ОБЪЩЧБЕФУС ЖЙЪЙЮЕУЛБС ЧЕМЙЮЙОБ, ТБЧОБС ПФОПЫЕОЙА ЙЪНЕОЕОЙС ХЗМПЧПК УЛПТПУФЙ ∆ω = ω2 — ω1 ЧТБЭБАЭЕЗПУС ФЕМБ ЪБ РТПНЕЦХФПЛ ЧТЕНЕОЙ ∆t Л ДМЙФЕМШОПУФЙ ЬФПЗП РТПНЕЦХФЛБ:
еУМЙ ХЗМПЧБС УЛПТПУФШ ЪБ РТПЙЪЧПМШОЩЕ ПДЙОБЛПЧЩЕ РТПНЕЦХФЛЙ ЧТЕНЕОЙ ЙЪНЕОСЕФУС ПДЙОБЛПЧП ( ∆ω12 = ∆ω34 Й Ф.Д.), ФП εУТ = const (ТБЧОПРЕТЕНЕООПЕ ЧТБЭЕОЙЕ).
хЗМПЧЩН ХУЛПТЕОЙЕН (НЗОПЧЕООЩН ХЗМПЧЩН ХУЛПТЕОЙЕН) ЧТБЭБАЭЕЗПУС ФЕМБ Ч НПНЕОФ ЧТЕНЕОЙ t ОБЪЩЧБЕФУС ЧЕМЙЮЙОБ ε, ТБЧОБС РТЕДЕМХ, Л ЛПФПТПНХ УФТЕНЙФУС УТЕДОЕЕ ХЗМПЧПЕ ХУЛПТЕОЙЕ ЪБ РТПНЕЦХФПЛ ЧТЕНЕОЙ ПФ t ДП t + ∆t РТЙ ВЕУЛПОЕЮОПН ХНЕОШЫЕОЙЙ ∆t, ЙМЙ, ХЗМПЧПЕ ХУЛПТЕОЙЕ — ЬФП РЕТЧБС РТПЙЪЧПДОБС ПФ ХЗМПЧПК УЛПТПУФЙ РП ЧТЕНЕОЙ ЙМЙ ЧФПТБС РТПЙЪЧПДОБС ПФ ХЗМБ РПЧПТПФБ РП ЧТЕНЕОЙ:
йЪНЕОЕОЙЕ ∆ω ХЗМПЧПК УЛПТПУФЙ БВУПМАФОП ФЧЕТДПЗП ФЕМБ ЪБ РТПНЕЦХФПЛ ЧТЕНЕОЙ ∆t = t — t0 РТЙ ТБЧОПРЕТЕНЕООПН ЧТБЭБФЕМШОПН ДЧЙЦЕОЙЙ У ХЗМПЧЩН ХУЛПТЕОЙЕН ε: ∆ω = ε·∆t = ε(t — t0). еУМЙ РТЙ t0 = 0 ОБЮБМШОБС ХЗМПЧБС УЛПТПУФШ ФЕМБ ТБЧОБ ω0, ФП Ч РТПЙЪЧПМШОЩК НПНЕОФ ЧТЕНЕОЙ t ХЗМПЧБС УЛПТПУФШ ФЕМБ ВХДЕФ ω = ω0 + ε·t.
хЗПМ РПЧПТПФБ ∆φ ФЕМБ ЧПЛТХЗ ПУЙ ЪБ РТПНЕЦХФПЛ ЧТЕНЕОЙ ∆t = t — t0 РТЙ ТБЧОПРЕТЕНЕООПН ДЧЙЦЕОЙЙ:
фБОЗЕОГЙБМШОБС УПУФБЧМСАЭБС ХУЛПТЕОЙС:

оПТНБМШОБС УПУФБЧМСАЭБС ХУЛПТЕОЙС:
фБЛЙН ПВТБЪПН, УЧСЪШ НЕЦДХ МЙОЕКОЩНЙ Й ХЗМПЧЩНЙ ЧЕМЙЮЙОБНЙ ЧЩТБЦБЕФУС УМЕДХАЭЙНЙ ЖПТНХМБНЙ: S = R·φ, υ = ω·R, aτ = R·ε, an = ω 2 ·R.
Кинематика поступательного движения
Тема 3
«Кинематика поступательного движения»
В соответствии с изложенным во второй лекции начнем изучение с поступательного движения.
Кинематика – раздел механики, описывающий механическое движение без изучения причин его вызвавших.
Для описания перемещения тела в пространстве (а это и есть механическое движение) введем систему отсчета и будем использовать модель матеиальной точки.
По отношению к системе отсчета положение точки А в данный момент времени в декартовой системе координат, используемой наиболее часто, определяется тремя координатами: 

При движении материальной точки ее координаты с течением времени изменяются. Уравнение выражающие зависимость радиус – вектора движущийся точки от времени 
 |
называются уравнениями движения точки или законом движения.
Введем еще несколько необходимых понятий.
Траектория движения материальной точки – линия, описываемая этой точкой в пространстве. Это не очень точное, хотя простое и понятное определение. Точнее было бы сказать, что траектория – это геометрическое место точек, последовательно занимаемых телом в процессе движения.
В зависимости от формы траектории движения подразделяются на прямолинейные и криволинейные. Если все точки траектории лежат в одной плоскости, движение называется плоским.
Траектории механического движения в различных системах отсчета могут иметь неодинаковую форму. Исследуя пространственно – временное перемещение тел, кинематика оперирует следующими физическими величинами – время, длина пути, перемещение, скорость движения и ускорение.
Рассмотрим движение материальной точки по произвольной траектории. Отсчет времени начнем с момента, когда точка находилась в положении А (см. рисунок 2).
Длиной пути называется длина участка траектории АВ, пройденного материальной точкой с момента начала отсчета времени. Длина пути является скалярной функцией времени
Перемещением называется вектор 
Средней скоростью 
называется физическая величина
 |
Направление вектора средней скорости совпадает с направлением вектора перемещения 

Мгновенной скоростью в момент времени называется физическая величина, равная пределу, к которому стремится средняя скорость при бесконечном уменьшение интервала времени
В математике такой предел называется производной, поэтому
 |
Вектор мгновенной скорости 


Мгновенным ускорением материальной точки в момент времени t называется физическая величина, равная пределу, к которому стремится среднее ускорение при бесконечном уменьшении интервала времени
 |
Направление среднего ускорения совпадает с направлением вектора 
С мгновенным ускорением дело обстоит сложнее, поэтому рассмотрим это подробно.
Как всякий вектор, вектор ускорения при произвольном плоском движении (например, вращательном) материальной точки можно представить в виде суммы его составляющих по двум взаимно перпендикулярным направлениям. В качестве одного направления выберем направление касательной в рассматриваемой точке траектории, тогда другим перпендикулярным направлением окажется направление нормали к кривой в этой же точке.
Составляющая ускорения, направленная по касательной к траектории, называется тангенциальной составляющей ускорения (
Вектор направлен в сторону движения точки при возрастании ее скорости и в противоположенную сторону – при убывании скорости.
Тангенциальная составляющая ускорения численно равна производной скорости по времени и характеризует быстроту изменения скорости по численному значению.
 |
Вторая составляющая называется нормальной составляющей ускорения (

где R – радиус криволинейной траектории в данной точке (радиус вписанной окружност и). Способ определения радиуса кривизны произвольной кривой излагается в специальной математической дисциплине, которая называется дифференциальная геометрия.
Таким образом, мгновенное ускорение представляется в следующем виде
 |
При этом величина ускорения равна
Рассмотренная процедура определения скорости и ускорения по заданному закону движения называется прямой задачей кинематики.
Данное определение можно представить в виде диаграммы
Прямая задача кинематики
 |
Указанная задача решается с помощью операции дифференцирования.
Задачу определения скорости и закона движения по заданному ускорению естественно называть обратной задачей кинематики.
Обратная задача кинематики
 |
Естественно, что эта задача решается с помощью операции интегрирования
 |
 |
 |
 |
Первая и третья формулы соответствуют решению в общем случае, а вторая и четвертая — для постоянного ускорения.
Следует отметить, что указанное решение обратной задачи справедливо только в том случае когда ускорение является функцией только времени. Однако, в большинстве интересных для приложений задач ускорение является функцией координат или скорости. Окончательное решение обратной задачи, поэтому, возможно только в рамках динамики, о чем будет рассказано в соответствующем месте.
Рассмотренные в данной лекции определения позволяют ввести новое понятие – понятие состояния. Под состоянием обычно понимают минимальный набор величин, который дает возможность предсказывать дальнейшее поведение системы.
Для классической механики таким набором будут радиус-вектор и скорость (или радиус-вектор и импульс), а для квантовой механики – волновая функция 
Кинематика поступательного движения материальной точки
Механика представляет собой учение о простейшей форме движения материи, которое состоит в перемещении тел или их частей друг относительно друга. Кинематика изучает движение тел вне зависимости от тех причин, которые обусловливают это движение.
Иногда при рассмотрении движения тел можно пренебречь их размерами. Тело, размерами которого в условиях данной задачи можно пренебречь, называется материальной точкой.
Поступательное движение – это такое движение, при котором любая прямая, связанная с движущимся телом, остается параллельной самой себе.
Материальная точка при своем движении описывает некоторую линию – траекторию.
Путь (S) – это длина траектории.
Если тело движется из точки 1 в точку 2, то вектор, проведенный из точки 1 в точку 2, называется перемещением ( 
Векторный способ описания движения.
Положение материальной точки в пространстве можно задать с помощью ее радиус-вектора 



Пусть тело движется из точки с радиус-вектором 





 |
D



При бесконечно малом перемещении бесконечно малый промежуток времени можно обозначить как dt, тогда ½d
Скорость 



Модуль скорости: v = ½ 

Вектор скорости 


Движение, при котором скорость, изменяясь как угодно по направлению, остается постоянной по величине, называется равномерным. При таком движении скорость равна пути S, деленному на время t, за которое он пройден:
Если при движении тела изменяется величина скорости, то такое движение называют ускоренным.
Ускорение 

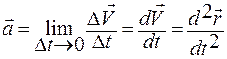
Прямолинейное движение с постоянным ускорением называется равнопеременным.
Кинематика движения материальной точки с постоянным ускорением:


Прямая задача кинематики позволяет найти при заданном уравнении траектории скорость и ускорение материальной точки:

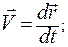

Обратная задача кинематики позволяет найти при заданных ускорении или скорости уравнение траектории материальной точки:
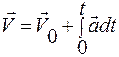
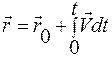
Координатный способ описания движения.
Если с телом отсчета жестко связать какую-нибудь координатную систему (например, декартову), то положение частицы (материальной точки) в любой момент времени определяется тремя ее координатами x(t), y(t), z(t):



Здесь 
Формулы для определения пройденного пути, модулей скорости частицы и ее ускорения:


Обратная задача кинематики:
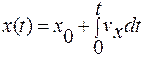

Кинематика движения материальной точки с постоянным ускорением:


В случае движения материальной точки по произвольной плоской кривой вектор полного ускорения будет равен
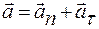


Вектор 


Вектор 
Модуль полного ускорения:


Между линейными и угловыми величинами существует следующая связь:
Здесь w – угловая скорость тела, e – угловое ускорение.
Пример 10. Радиус-вектор частицы изменяется со временем по закону 
Дано: 
А = 1 м/с 2 , В = 2 м/с, С = 1 м;
Решение. Путь, пройденный частицей за 2 секунды после начала движения найдем из (1.3.23) с учетом (1.3.21):

Подставим полученные значения координат частицы в (1.3.23) и рассчитаем пройденный частицей путь:

Величину скорости и ускорения частицы через указанный в условии задачи промежуток времени также найдем, используя формулу (1.3.23) с учетом (1.3.22):


v = (4 2 + 2 2 + 0 2 ) 1/2 = 4,5 (м/с).
a = (2 2 + 0 2 + 0 2 ) 1/2 = 2 (м/с 2 ).
Ответ: 5,7 м; 4,5 м/с; 2 м/с 2 .
Пример 11. Частица начала движение из начала координат по плоской криволинейной траектории радиуса 1 м. Радиус-вектор частицы зависит от времени по закону 
Дано: 
А = 1 м/с 3 , В = 2 м/с, С = 3 м;
Решение. Модуль нормального ускорения найдем с помощью формулы (1.3.30), учитывая (1.3.23) и (1.3.22):

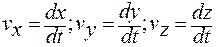
Подставим в вышеприведенные формулы числовые данные, получим:
v = (3 2 + 2 2 + 0 2 ) 1/2 = 3,6 (м/с); an = v 2 /R = 3,6 2 /1 = (13 м/с 2 ).
1.3.6. Кинематика вращательного движения вокруг неподвижной оси
Абсолютно твердое тело (АТТ) – это система частиц, расстояния между которыми в процессе движения тела неизменны.
Всякое движение твердого тела можно разложить на два основных движения – поступательное и вращательное.
При вращательном движении все точки тела движутся по окружностям, центры которых лежат на одной и той же прямой, называемой осью вращения. Ось вращения может находиться вне тела.
Радиус-вектор каждой точки (вектор, проведенный из центра соответствующей окружности в данную точку) поворачиваются за время Dt на один и тот же угол Dj – угол поворота твердого тела.
Поворот тела на некоторый угол (бесконечно малый) dj задают в виде отрезка, длина которого равна dj , а направление совпадает с осью, вокруг которой совершен поворот.
Векторы типа 

называется угловой скоростью АТТ. Вектор 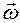

При равномерном вращении
При одном полном обороте на время t = T тело поворачивается на угол j = 2p:
где Т – период вращения.
Число оборотов в единицу времени называется частотой вращения:
При неравномерном вращении говорят, что тело вращается с ускорением (угловым)

При увеличении угловой скорости со временем вектор угловой скорости и вектор углового ускорения сонаправлены (ускоренное движение). В случае замедленного движения эти векторы противонаправлены.
Обратная задача кинематики вращательного движения:
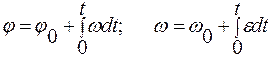
Для равноускоренного (равнозамедленного) вращения:
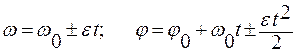
Пример 12. Частица из состояния покоя начала ускоренное вращение по окружности радиуса 1 м, угол поворота зависит от времени по закону j(t) = Аt 3 . Найти через 1 секунду после начала движения: 1) отношение тангенциального и нормального ускорений; 2) величину полного ускорения частицы. А = 1 рад/с 3 .
Решение. Тангенциальное и нормальное ускорения частицы найдем с помощью формул (1.3.28) и (1.3.30) с учетом (1.3.29), (1.3.31) и (1.3.35):
Нормальное ускорение: an = v 2 /R, связь между линейной и угловой скоростями: v = wR = 3 (м/с), поэтому an= 3 2 /1 = 9 (м/с 2 ).
Отношение тангенциального и нормального ускорений:
Полное ускорение частицы найдем из (1.3.27):

Ответ: 0,67; 10,8 м/с 2 .
Пример 13. Диск радиуса 1 м начал вращаться вокруг своей оси так, что угол его поворота зависит от времени по закону
j(t) = Аt 3 – Вt 2 . Через сколько секунд диск остановится, если
А = 1 рад/с 3 , В = 1 рад/с 2 ?
А = 1 рад/с 3 , В = 1 рад/с 2 .
Решение. Время остановки диска находим из условия, что его конечная угловая скорость равна нулю: w = 0.
Вращение диска по условию задачи не является равнопеременным, поэтому для нахождения зависимости угловой скорости от времени используем формулу (1.3.31):

Теперь используем условие равенства нулю угловой скорости, приравняв к нулю полученное выражение, и найдем время остановки диска:
Имеем два корня уравнения:
Ответ: диск остановится через 0,67 секунды.
http://pandia.ru/text/79/107/20640.php
http://lektsii.org/3-129488.html


























 (Ф.Л. Б1И= — Б1; И01 = 0);
(Ф.Л. Б1И= — Б1; И01 = 0); (Ф.Л. v2x = — v02 Й a2x = — a2).
(Ф.Л. v2x = — v02 Й a2x = — a2). , ПФЛХДБ v01·t1 + v02·t1 = И02, Ф.Л. Б1 = Б2,
, ПФЛХДБ v01·t1 + v02·t1 = И02, Ф.Л. Б1 = Б2,


































































