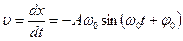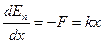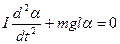Уравнение кинетической энергии для гармонических колебаний

Кинетическая, потенциальная и полная энергии гармонических колебаний

Лекция 5. Механические колебания

План лекции

5.1. Основные характеристики колебательного движения.

5.2. Кинетическая, потенциальная и полная энергии гармонических колебаний.

5.3. Уравнение гармонических колебаний. Маятники.

5.4. Затухание колебания.

5.5. Вынужденные колебания. Резонанс.

5.6. Явление резонанса в строительстве.

Основные характеристики колебательного движения

Процессы точно или приблизительно повторяющиеся через одинаковые промежутки времени называются колебаниями.В зависимости от физической природы различают механические, электромагнитные и другие виды колебаний. Несмотря на разную природу колебаний, в них обнаруживаются одни и те же физические закономерности, они описываются одними и теми же математическими уравнениями и исследуются общими методами, разработка и применение которых составляют задачу теории колебаний.

В данном курсе физики мы будем изучать два наиболее распространенных класса колебаний: механические и электрические.

Среди разнообразных колебаний основную и существенную роль играют так называемые гармонические колебания, то есть такие, при которых колеблющаяся величина изменяется с течением времени по закону синуса или косинуса.

Рассмотрим гармонические колебания на примере колеблющейся точки.

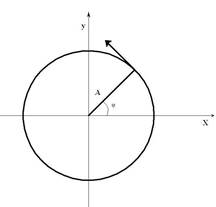
Пусть точка вращается по окружности радиуса А с угловой скоростью ω₀ (рис.5.1).

Рис.5.1.

Если точку спроецировать на оси X и Y, то ее проекции будут совершать колебания и удовлетворяют следующим уравнениям соответственно

, (5.1)

и (5.2)

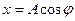
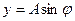
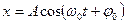
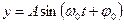
где х и y – смещения колеблющейся точки от положения равновесия;

А – амплитуда колебания (максимальное смещение);

ω₀ – круговая (циклическая) частота колебаний.

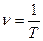
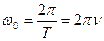
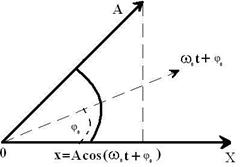
Точка совершает одно полное колебание за время Τ, называемое периодом колебания. Частота колебаний ν (число колебаний в единицу времени) есть . Между указанными величинами существует взаимосвязь

(5.3)

Геометрический смысл параметров уравнений (5.2) можно объяснить с помощью векторных диаграмм. Выберем на оси Х точку О и из этой точки под углом φ₀ проведем вектор А. Будем вращать вектор А с угловой скоростью ω₀ и тогда его проекция на ось будет смещаться на величину x (рис. 5.2).

Рис.5.2.

Колеблющаяся точка обладает скоростью и ускорением. Скорость материальной точки

(5.4)

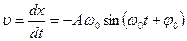
Ускорение материальной точки

(5.5)

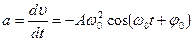
С учетом формулы (5.2) получим

(5.6)

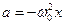
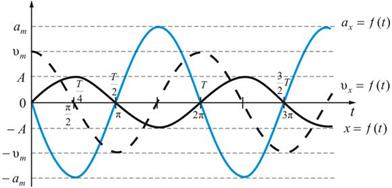
Сравнивая уравнения (5.2), (5.4) и (5.5) замечаем, что скорость опережает смещение на π/2. Фазы ускорения и смещения различаются на π (изменяются в противофазе). Графические зависимости смещения, скорости и ускорения от времени показаны на рис.5.3.

Умножив обе части равенства уравнения (5.6) на массу m материальной точки получим

(5.7)

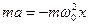
Используя II закон Ньютона, получаем

(5.8)

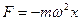
Рис.5.3.

Таким образом, чтобы совершались гармонические колебания на материальную точку должна действовать сила F, пропорциональная смещению x, которая возвращает ее в положение равновесия

(5.9)

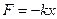
где, k – некоторый коэффициент (зависящий от свойств колеблющейся системы) и называемой жесткостью.

Из уравнения (5.7) и (5.8) видно, что .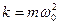

Кинетическая, потенциальная и полная энергии гармонических колебаний

Полная энергия Е колеблющейся материальной точки равна сумме кинетической Е_к и потенциальной Е_п энергий

Кинетическую энергию можно найти, зная массу m и скорость u

(5.11)

(5.12)

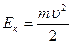
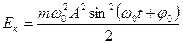
Выражение для потенциальной энергии можно найти из соотношений между потенциальной энергией и силой.

(5.13)

(5.14)

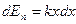
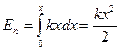
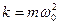
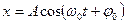
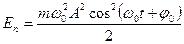
Учитывая, что и получаем

(5.15)

Полную энергию получим сложив (5.12) и (5.15)

(5.16)

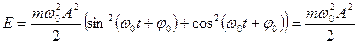
Таким образом, полная энергия пропорциональна квадрату амплитуды колебаний.

Из формул (5.12) и (5.15) видно, что когда 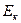увеличивается Е_п уменьшается и наоборот.

5.3. Уравнение гармонических колебаний.
Маятники

На колеблющуюся материальную точку массой m действует возвращающая сила F = — kx. Эта сила вызывает ускорение 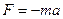. Равенство этих сил позволяет записать

где, k – жесткость системы, 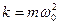; х – смещение; а – ускорение материальной точки.

Сделав соответствующие подстановки в (5.17), получим

или (5.18)

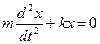
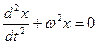
Уравнение (5.18) представляет собой дифференциальное уравнение второго порядка незатухающих гармонических колебаний материальной точки.

Решением этого дифференциального уравнения как раз и является уравнение (5.2): .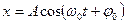

Колебания любого гармонического осциллятора (или гармонического вибратора) описываются дифференциальным уравнением второго порядка

(5.19)

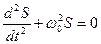
Решением этого уравнения является

(5.20)

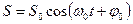
где S₀ – амплитудное (максимальное) значение параметра S.

Примерами гармонических осцилляторов являются маятники, колебательный контур.

В качестве примера малых колебаний рассмотрим колебания маятников.

Пружинный маятник

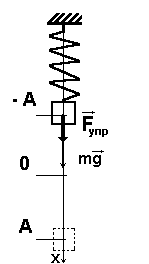
Груз массой m, подвешенный на упругой пружине представляет собой пружинный маятник (рис.5.4). Если груз оттянуть вниз и отпустить, то под действием силы F = -kx маятник будет совершать колебания; k – коэффициент жесткости (в данном случае коэффициент упругости).

Рис.5.4.

Уравнение движения маятника имеет вид

или ,

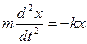
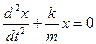
Его решением является

Это значит, что пружинный маятник совершает гармонические колебания с циклической частотой ω₀

, с другой стороны .

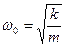
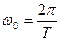
Период колебаний пружинного маятника

(5.21).

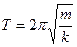
Физический маятник

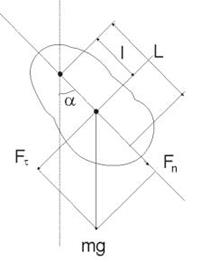
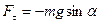
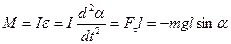
Физическим маятником называется твердое тело, которое может колебаться под действием силы тяжести вокруг оси, не проходящей через центр масс. При отклонении маятника относительно оси О угол α, на него действует М – момент возвращающей силы (рис.5.5)

(5.22)

где, I – момент инерции относительно оси О;

l – плечо силы F_τ; при малых углах .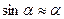

Рис.5.5.

Из (5.22) получаем дифференциальное уравнение

(5.23)

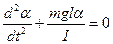
Сравнив уравнение (5.23) с уравнением гармонического осциллятора (5.19), получим

, (5.24)

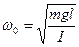
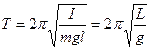
где, 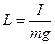– приведенная длина физического маятника.

От точки подвеса О на линии ОС на расстоянии L находится точка О₁, называемая центром качения. Точки О и О₁ обладает свойством взаимозаменяемости.

Гармонические колебания

О чем эта статья:

9 класс, 11 класс, ЕГЭ/ОГЭ

Механические колебания

Механические колебания — это физические процессы, которые точно или приблизительно повторяются через одинаковые интервалы времени.

Колебания делятся на два вида: свободные и вынужденные.

Свободные колебания

Это колебания, которые происходят под действием внутренних сил в колебательной системе.

Они всегда затухающие, потому что весь запас энергии, сообщенный в начале, в конце уходит на совершение работы по преодолению сил трения и сопротивления среды (в этом случае механическая энергия переходит во внутреннюю). Из-за этого свободные колебания почти не имеют практического применения.

Вынужденные колебания

А вот вынужденные колебания восполняют запас энергии внешним воздействием. Если это происходит каждый период, то колебания вообще затухать не будут.

Вынужденные колебания — это колебания, которые происходят под действием внешней периодически меняющейся силы.

Частота, с которой эта сила воздействует, равна частоте, с которой система будет колебаться.

Например, качели. Если вас кто-то будет на них качать, каждый раз давая толчок, когда вы приходите в одну и ту же точку — такое колебание будет считаться вынужденным.

Это колебание все еще будет считаться вынужденным, если вас будут раскачивать из положения равновесия. Просто в данном случае амплитуда (о которой речь пойдет чуть ниже) будет увеличиваться с каждым колебанием.

Автоколебания

Иногда вынужденному колебанию не нужно внешнего воздействия, чтобы случиться. Бывают такие системы, в которых это внешние воздействие возникает само из-за способности регулировать поступление энергии от постоянного источника.

У автоколебательной системы есть три важных составляющих:

• сама колебательная система
• источник энергии
• устройство обратной связи, обеспечивающей связь между источником и системой

Часы с кукушкой — пример автоколебательной системы. Гиря на ниточке (цепочке) стремится вращать зубчатое колесо (храповик). При колебаниях маятника анкер цепляет за зубец, и вращение приостанавливается.

Но в результате маятник получает толчок, компенсирующий потери энергии из-за трения. Потенциальная энергия гири, которая постепенно опускается, расходуется на поддержание незатухающих колебаний.

Характеристики колебаний

Чтобы перейти к гармоническим колебаниям, нам нужно описать величины, которые помогут нам эти колебания охарактеризовать. Любое колебательное движение можно описать величинами: период, частота, амплитуда, фаза колебаний.

Период — это время одного полного колебания. Измеряется в секундах и обозначается буквой T.

Формула периода колебаний

T = t/N

N — количество колебаний [—]

Также есть величина, обратная периоду — частота. Она показывает, сколько колебаний совершает система в единицу времени.

Формула частоты

ν = N/t = 1/T

N — количество колебаний [—]

Амплитуда — это максимальное отклонение от положения равновесия. Измеряется в метрах и обозначается либо буквой A, либо x max .

Она используется в уравнении гармонических колебаний:

Гармонические колебания

Простейший вид колебательного процесса — простые гармонические колебания, которые описывают уравнением:

Уравнение гармонических колебаний

x — координата в момент времени t [м]

t — момент времени [с]

(2πνt) в этом уравнении — это фаза. Ее обозначают греческой буквой φ

Фаза колебаний

t — момент времени [с]

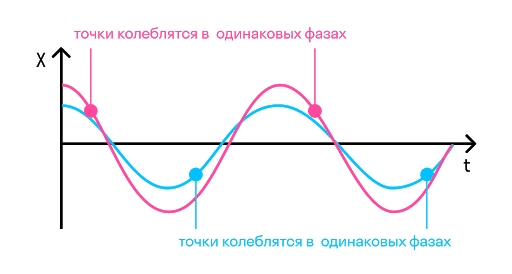
Фаза колебаний — это физическая величина, которая показывает отклонение точки от положения равновесия. Посмотрите на рисунок, на нем изображены одинаковые фазы:

Например, в тех же самых часах с кукушкой маятник совершает колебания. Он качается слева направо и приходит в самую правую точку. В той же фазе он будет находиться, когда придет в ту же точку, идя справа налево. Если мы возьмем точку на сантиметр левее самой правой, то идя в нее не слева направо, а справа налево, мы получим уже другую фазу.

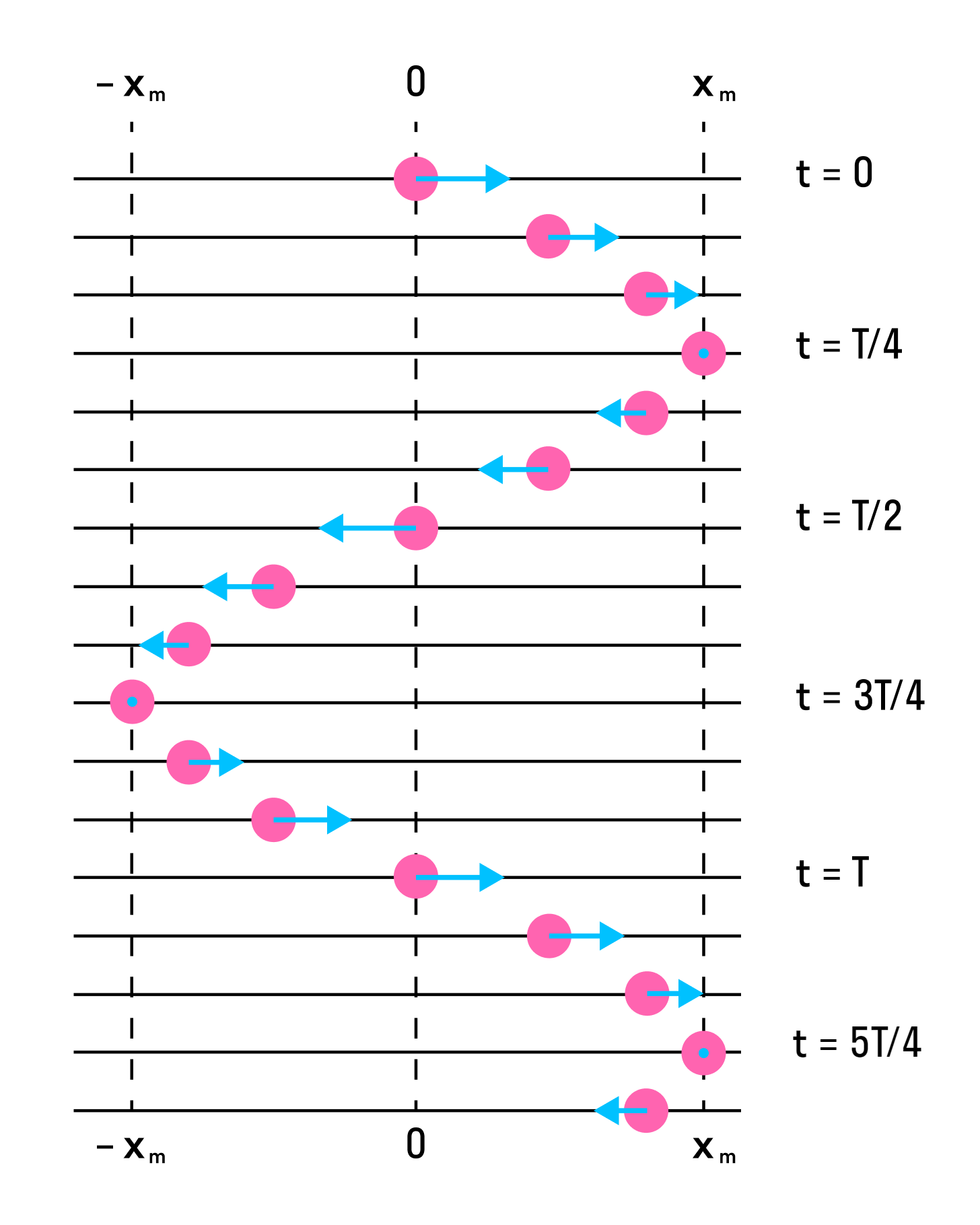
На рисунке ниже показаны положения тела через одинаковые промежутки времени при гармонических колебаниях. Такую картину можно получить при освещении колеблющегося тела короткими периодическими вспышками света (стробоскопическое освещение). Стрелки изображают векторы скорости тела в различные моменты времени.

Если изменить период, начальную фазу или амплитуду колебания, графики тоже изменятся.

На рисунке ниже во всех трех случаях для синих кривых начальная фаза равна нулю, а в последнем (с) — красная кривая имеет меньшую начальную фазу.

В первом случае (а) красная кривая описывает колебание, у которого амплитуда больше колебания, описанного синей линией.

Во втором случае (b) красная кривая отличается от синей только значением периода — у красной период в два раза меньше.

Математический маятник

Математический маятник — отличный пример гармонических колебаний. Если мы подвесим шарик на нити, то это еще не будет математическим маятником — пока он только физический.

Математическим этот маятник станет, если размеры шарика много меньше длины нити (тогда этими размерами можно пренебречь и рассматривать шарик как материальную точку), растяжение нити очень мало, а масса нити во много раз меньше массы шарика.

Математическим маятником называется система, которая состоит из материальной точки массой m и невесомой нерастяжимой нити длиной l, на которой материальная точка подвешена, и которая находится в поле силы тяжести (или других сил).

Период малых колебаний математического маятника в поле силы тяжести Земли определяется по формуле:

Формула периода колебания математического маятника

l — длина нити [м]

g — ускорение свободного падения [м/с 2 ]

На планете Земля g = 9,8 м/с 2

Пружинный маятник

Пружинный маятник — это груз, прикрепленный к пружине, массой которой можно пренебречь.

В пружинном маятнике колебания совершаются под действием силы упругости.
Пока пружина не деформирована, сила упругости на тело не действует.

Формула периода колебания пружинного маятника

m — масса маятника [кг]

k — жесткость пружины [Н/м]

Закон сохранения энергии для гармонических колебаний

Физика — такая клевая наука, в которой ничего не исчезает бесследно и не появляется из ниоткуда. Эту особенность описывает закон сохранения энергии.

Рассмотрим его на примере математического маятника.

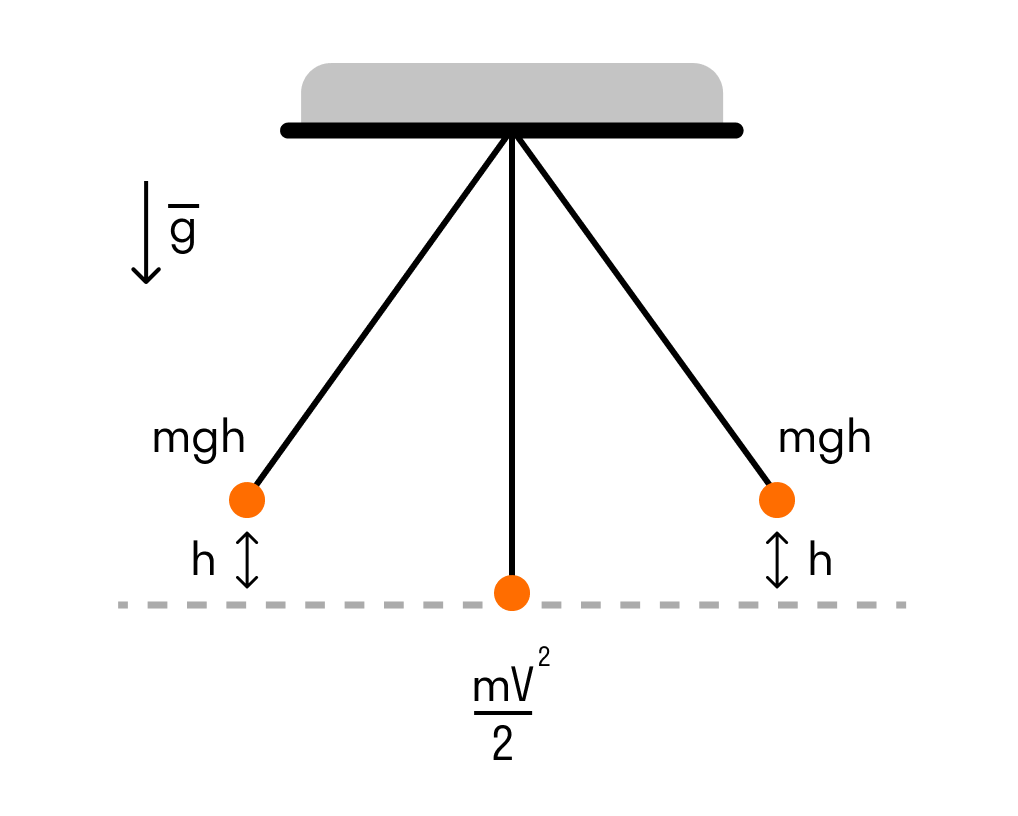
• Когда маятник отклоняют на высоту h, его потенциальная энергия максимальна.
• Когда маятник опускается, потенциальная энергия переходит в кинетическую. Причем в нижней точке, где потенциальная энергия равна нулю, кинетическая энергия максимальна и равна потенциальной энергии в верхней точке. Скорость груза в этой точке максимальна.

Онлайн-курсы физики в Skysmart не менее увлекательны, чем наши статьи!

Энергия гармонических колебаний

Вы будете перенаправлены на Автор24

Колебания — это самая общая форма движения динамических систем около положения равновесия. При малых отклонениях от положения равновесия колебания обычно являются гармоническими. В этом заключается их особенная значимость.

где $\omega^2$ — циклическая частота колебаний; $x$ -расстояние положения равновесия

называют уравнением механических гармонических колебания. Колебания происходят вдоль оси $X$.

Решением уравнения (1) можно считать функции:

$x=A\sin (\omega t+\varphi)$ или

$x=A\cos (\omega t+\varphi_1)$,

где $A$ — амплитуда колебаний.

Систему, которая реализует данные малые колебания, называют линейным или гармоническим осциллятором. Примером гармонического осциллятора может служить

1. малое тело, подвешенное на упругую пружину (Пружинный маятник);
2. физический маятник (Тело, которое совершает колебания относительно точки (или оси, проходящей через точку тела), не являющейся его центром масс);
3. математический маятник; (Малое тело, совершающее колебания на длинном, нерастяжимом, невесомом подвесе).

Собственными называют колебания системы под воздействием только внутренних сил при отсутствии внешних воздействий.

В полной механической энергии гармонического осциллятора выделяют:

• потенциальную энергию;
• и кинетическую энергию.

Потенциальная энергия

Говорить о потенциальной энергии можно только, если действующие силы потенциальны. Если колебательные движения между двумя точками являются одномерным, то автоматически обеспечивается условие потенциальности и всякую силу, зависящую только от координат, можно считать потенциальной.

Если рассматривается линейный осциллятор, то обычно считают, что потенциальная энергия точки равна нулю в положении равновесия. Считая, что осциллятор заставляет совершать колебания сила упругости;

и зная, как связана потенциальная энергия и потенциальная сила, (для одномерного случая: $F=-\frac$), потенциальную энергию линейного осциллятора определим как:

Готовые работы на аналогичную тему

Из формулы (3) видно, что потенциальная энергия при колебаниях изменяется с течением времени, так как изменяется $x$. Частота колебаний потенциальной энергии $2\omega$.

Кинетическая энергия.

Кинетическая энергия тела – это энергия движения, она зависит от скорости перемещения материальной точки, задается выражением:

Кинетическая энергия является переменной во времени физической величиной. Колебания ее происходят с частотой $2\omega$ (эта частота в два раза больше, чем частота колебаний $x$)

Закон сохранения энергии при гармонических колебаниях

Как было отмечено, кинетическая энергия и потенциальная энергия являются переменными во времени величинами, однако, их сумма у гармонического осциллятора, выполняющего свободные колебания, не изменяется:

Полная энергия системы ($E$) не изменяется, поскольку при гармонических колебаниях выполняется закон сохранения механической энергии, так как сила упругости является консервативной.

Закон сохранения энергии позволяет сделать два существенных вывода

Вывод первый. Наибольшая кинетическая энергия осциллятора равна его наибольшей энергии потенциальной энергии.

Данный вывод очевиден, так как потенциальная энергия осциллятора максимальна при смещении точки выполняющей колебания на максимально возможное расстояние, при этом скорость, а соответственно и кинетическая энергия осциллятора равна нулю.

Наибольшую кинетическую энергию колебательная система имеет тогда, когда она проходит положение равновесия ($x=0$), то есть потенциальная энергия равна нулю.

где $V$ — максимальная скорость.

Вывод второй. Средняя кинетическая энергия осциллятора равна его средней потенциальной энергии.

Средняя кинетическая энергия.

Пусть параметр $f$ функция времени, тогда средняя ее величина на отрезке времени от $t_1$ до $t_2$ равна:

где пределы интегрирования обозначают 1 — время $t_1$; 2 — $t_2$.

Если функцию $f(t)$ изобразить на графике (рис.1), то ее среднее значение будет соответствовать высоте прямоугольника, площадь которого ограничивают функция $f$ и ось $t$ на заданном отрезке времени.

Площадь под осью $t$ считают отрицательной.

Рисунок 1. График. Автор24 — интернет-биржа студенческих работ

Запишем закон движения осциллятора как:

$x(t)=A\cos (\omega t+\varphi) (7)$,

его скорость равна:

$\dot=-A\omega\sin (\omega t+\varphi) (8).$

Выражение для потенциальной энергии представим как:

Кинетическую энергию представит выражение:

Отрезком времени, на котором будем брать среднее, станет период колебаний, вернее одного колебания. Нахождение средних значений кинетической и потенциальной энергии сводят к поиску средних от $\cos^2 (\omega t+\varphi)$ и $\sin^2 (\omega t+\varphi)$:

$(\sin^2 (\omega t+\varphi))_=\frac<1>\int_0^T \cos^2 (\omega t+\varphi)dt=\frac<1>\int_0^T\frac<1><2>(1-\cos 2(\omega t+\varphi)dt)=\frac<1><2>,$

где $T$ — период колебаний; $\omega T=2\pi.$

По аналогии получаем:

$\sin^2 (\omega t+\varphi)_sr=\frac<1><2>.$

В результате имеем:

средняя по времени потенциальная энергия гармонического колебания за один период равна:

средняя по времени кинетическая энергия составила:

Сравнивая (10) и (11) мы видим, что:

где $E$ — полная механическая энергия гармонических колебаний.

то есть средняя по времени кинетическая энергия осциллятора равна средней по времени потенциальной энергии.

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 22 05 2021