Техническая механика
Динамика системы материальных точек
Уравнение поступательного движения твердого тела
Механической системой материальных точек называется совокупность материальных точек, каким-то образом связанных межу собой.
Всякое твердое тело можно считать неизменяемой механической системой материальных точек. Силы взаимодействия точке данной системы называются внутренними силами; силы, с которыми действуют на данную систему другие точки, не входящие в эту систему, — внешними.
Пусть твердое тело массой m движется под действием силы F поступательно с ускорением а (рис. 1) .
Разобьем тело на ряд материальных точек с массами m1 и применим принцип Даламбера, не забывая при этом, что внутренние силы в уравнение равновесия не входят, так как на основании третьего закона Ньютона их сумма для системы в целом равна нулю.
В каждой материальной точке приложим силу инерции Fi ин = — mia и составим уравнение равновесия:
ΣX = 0 ; F – ΣFi ин = 0 ,
Так как при поступательном движении все точки тела имеют одинаковые ускорения, то а можно вынести за знак суммы, т. е.
Согласно второму закону Ньютона векторы силы F и ускорения а совпадают по направлению, поэтому можно записать:
Это и есть уравнение поступательного движения твердого тела. Очевидно, что это уравнение ничем не отличается от основного уравнения динамики точки, следовательно, все формулы динамики точки применимы для тела, движущегося поступательно.
Уравнение вращательного движения твердого тела
Пусть твердое тело под действием системы сил вращается вокруг неподвижной оси z с угловым ускорением α (рис. 2) .
Разобьем тело на ряд материальных точек с массами mi и применим, как и в предыдущем случае, принцип Даламбера (Д’Аламбера).
К каждой материальной точке приложены касательная и нормальная силы инерции. Составим уравнение равновесия:
Моменты реакций подшипника и подпятника, а также сил Fτi ин относительно оси z равны нулю, так как линии действия этих сил пересекают ось; сумма моментов внешних сил относительно оси вращения называется вращающим моментом .
Тогда
Выражение Σ(miri 2 ) называют моментом инерции тела относительно оси и обозначают J :
Момент инерции тела относительно оси есть сумма произведений масс материальных точек, составляющих это тело, на квадрат расстояния от них до этой оси.
В результате получим формулу:
которая называется уравнением вращательного движения твердого тела. В этой формуле J – момент инерции тела относительно оси вращения.
Единица момента инерции — [J] = [mr 2 ] = [m][r 2 ] = кг×м 2 .
Момент инерции играет во вращательном движении такую же роль, какую масса играет в поступательном движении, т. е. момент инерции есть мера инертности вращающегося тела.
В качестве примера определим момент инерции тонкого однородного сплошного диска, радиус которого R , толщина s , масса m , относительно оси, перпендикулярной плоскости диска и проходящей через его центр О (см. рис 3) .
Разобьем диск на элементарные кольца переменного радиуса r , шириной dr и толщиной s . Согласно определению момент инерции такого кольца равен
dJ = dΣ(mir 2 ) = r 2 dΣmi = r 2 dm = r 2 2πr drsρ = 2πsρ r 3 dr ,
где ρ – плотность материала диска.
Просуммировав моменты инерции всех элементарных колец, получим момент инерции всего диска:
J = ∫ 2πsρ r 3 dr = 2πsρ ∫ r 3 dr = 2πsρ r 4 /4 = πsρ r 4 /2 .
Так как масса диска m = πr 2 sρ , то можно записать: J = mR 2 /2 .
Нетрудно понять, что момент инерции однородного сплошного прямоугольного кругового цилиндра радиусом R и массой m любой высоты определяют по такой же формуле. Чтобы убедиться в этом, достаточно мысленно разбить цилиндр плоскостями, параллельными основанию на тонкие диски, и просуммировать моменты инерции всех дисков.
Моменты инерции тел вращения
На основе теоретических выкладок, изложенных выше, мы установили, что момент инерции круглого диска и цилиндрического тела можно определить по формуле
Аналогичные формулы можно вывести для определения моментов инерции других геометрических тел, наиболее часто встречающихся при расчетах и решении задач технической механики.
Моменты инерции для некоторых других однородных тел можно определить по формулам, которые приводятся здесь без вывода.
Шар массой m , радиусом R относительно диаметра:
Тонкий стержень массой m , длиной l относительно оси, проходящей перпендикулярно стержню через его конец:
Тонкая сферическая оболочка массой m , радиусом R относительно диаметра:
Пустотелый вал массой m , наружным радиусом R и радиусом отверстия r относительно оси:
Момент инерции Jz тела относительно какой-либо оси z , параллельной центральной (т. е. проходящей через центр тяжести С тела), равен сумме центрального момента инерции Jc и произведения массы m тела на квадрат расстояния а между этими осями:
Из этой формулы (ее вывод здесь не приводится) следует, что из всех моментов инерции тела относительно параллельных осей наименьшим будет момент инерции относительно центральной оси , т. е. центральный момент инерции.
Иногда момент инерции определяют по формуле: J = mrи 2 , где rи – радиус инерции тела :
Физический смысл радиуса инерции следующий: если массу тела сосредоточить в одной точке (такая масса называется приведенной) и поместить ее от оси вращения на расстоянии, равном радиусу инерции, то момент инерции приведенной массы будет равен моменту инерции данного тела относительно той же оси.
Удвоенный радиус инерции тела называется диаметром инерции : Dи = 2rи .
В практике иногда вместо момента инерции пользуются понятием махового момента GDи 2 .
Маховым моментом называется произведение силы тяжести G вращающегося тела на квадрат его диаметра инерции.
Единица махового момента — Н×м 2 .
Между маховым моментом и моментом инерции существует простая зависимость:
GDи 2 = 4g J = 39,24 J .
Кинетическая энергия твердого тела
Кинетическая энергия твердого тела равна сумме кинетических энергий материальных точек, составляющих данное тело:
Определим выражения для кинетической энергии твердого тела для трех случаев движения.
Тело движется поступательно
Учитывая, что при поступательном движении тела все его точки имеют одинаковую траекторию и одинаковые скорости, можно записать:
Следовательно, при поступательном движении твердого тела его кинетическая энергия вычисляется по той же формуле, что и кинетическая энергия материальной точки.
Тело вращается вокруг неподвижной оси
Кинетическая энергия твердого тела, вращающегося вокруг неподвижной оси, равна половине произведения момента инерции тела относительно оси вращения на квадрат его угловой скорости.
Тело движется плоскопараллельно
Как известно из кинематики, сложное плоскопараллельное движение твердого тела в каждый данный момент времени можно считать простейшим вращательным движением вокруг мгновенной оси (метод мгновенных центров скоростей) .
Допустим, что известна скорость vс центра тяжести тела, тогда мгновенная угловая скорость
где ОС – расстояние центра тяжести С тела от мгновенной оси вращения О .
Момент инерции Jо относительно мгновенной оси вращения определяют по формуле:
где Jс — момент инерции относительно центральной оси или центральный момент инерции.
Кинетическую энергию тела, движущегося плоскопараллельно, определяют следующим образом:
Кпп = Jоω 2 /2 = (Jс + mОС 2 ) ω 2 /2 = (Jсω 2 )/2 + mOC 2 /2×vс 2 /ОС 2 ,
Кинетическая энергия твердого тела, движущегося плоскопараллельно, равна сумме кинетических энергий в поступательном движении вместе с центром тяжести и вращательном движении вокруг центральной оси, перпендикулярной основной плоскости.
В заключение сформулируем теорему об изменении кинетической энергии системы тел:
Изменение кинетической энергии системы тел при некотором перемещении равно алгебраической сумме работ всех внешних (активных и реактивных) и внутренних сил, действовавших на систему при указанном перемещении:
Кинетическая энергия системы тел равна сумме кинетических энергий каждого тела в отдельности.
Если тело твердое, то сумма работ его внутренних сил равна нулю. При некоторых связях, называемых идеальными, работа реактивных сил тоже будет равна нулю.
Кинетическая и потенциальная энергии
Энергия — важнейшее понятие в механике. Что такое энергия. Существует множество определений, и вот одно из них.
Что такое энергия?
Энергия — это способность тела совершать работу.
Кинетическая энергия
Рассмотрим тело, которое двигалось под действием каких-то сил изменило свою скорость с v 1 → до v 2 → . В этом случае силы, действующие на тело, совершили определенную работу A .
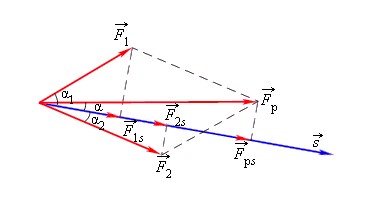
Работа всех сил, действующих на тело, равна работе равнодействующей силы.
F р → = F 1 → + F 2 →
A = F 1 · s · cos α 1 + F 2 · s · cos α 2 = F р cos α .
Установим связь между изменением скорости тела и работой, совершенной действующими на тело силами. Для простоты будем считать, что на тело действует одна сила F → , направленная вдоль прямой линии. Под действием этой силы тело движется равноускоренно и прямолинейно. В этом случае векторы F → , v → , a → , s → совпадают по направлению и их можно рассматривать как алгебраические величины.
Работа силы F → равна A = F s . Перемещение тела выражается формулой s = v 2 2 — v 1 2 2 a . Отсюда:
A = F s = F · v 2 2 — v 1 2 2 a = m a · v 2 2 — v 1 2 2 a
A = m v 2 2 — m v 1 2 2 = m v 2 2 2 — m v 1 2 2 .
Как видим, работа, совершенная силой, пропорционально изменению квадрата скорости тела.
Определение. Кинетическая энергия
Кинетическая энергия тела равна половине произведения массы тела на квадрат его скорости.
Кинетическая энергия — энергия движения тела. При нулевой скорости она равна нулю.
Теорема о кинетической энергии
Вновь обратимся к рассмотренному примеру и сформулируем теорему о кинетической энергии тела.
Теорема о кинетической энергии
Работа приложенной к телу силы равна изменению кинетической энергии тела. Данное утверждение справедливо и тогда, когда тело движется под действием изменяющейся по модулю и направлению силы.
A = E K 2 — E K 1 .
Таким образом, кинетическая энергия тела массы m , движущегося со скоростью v → , равна работе, которую сила должна совершить, чтобы разогнать тело до этой скорости.
A = m v 2 2 = E K .
Чтобы остановить тело, нужно совершить работу
A = — m v 2 2 =- E K
Потенциальная энергия
Кинетическая энергия — это энергия движения. Наряду с кинетической энергией есть еще потенциальная энергия, то есть энергия взаимодействия тел, которая зависит от их положения.
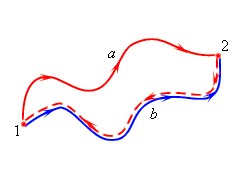
Например, тело поднято над поверхностью земли. Чем выше оно поднято, тем больше будет потенциальная энергия. Когда тело падает вниз под действием силы тяжести, эта сила совершает работу. Причем работа силы тяжести определяется только вертикальным перемещением тела и не зависит от траектории.
Вообще о потенциальной энергии можно говорить только в контексте тех сил, работа которых не зависит от формы траектории тела. Такие силы называются консервативными.
Примеры консервативных сил: сила тяжести, сила упругости.
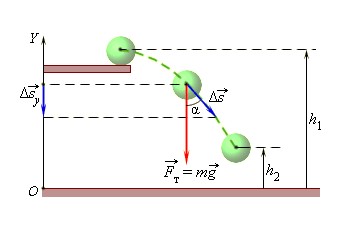
Когда тело движется вертикально вверх, сила тяжести совершает отрицательную работу.
Рассмотрим пример, когда шар переместился из точки с высотой h 1 в точку с высотой h 2 .
При этом сила тяжести совершила работу, равную
A = — m g ( h 2 — h 1 ) = — ( m g h 2 — m g h 1 ) .
Эта работа равна изменению величины m g h , взятому с противоположным знаком.
Величина Е П = m g h — потенциальна энергия в поле силы тяжести. На нулевом уровне (на земле) потенциальная энергия тела равна нулю.
Определение. Потенциальная энергия
Потенциальная энергия — часть полной механической энергии системы, находящейся в поле консервативных сил. Потенциальная энергия зависит от положения точек, составляющих систему.
Можно говорить о потенциальной энергии в поле силы тяжести, потенциальной энергии сжатой пружины и т.д.
Работа силы тяжести равна изменению потенциальной энергии, взятому с противоположным знаком.
A = — ( E П 2 — E П 1 ) .
Ясно, что потенциальная энергия зависит от выбора нулевого уровня (начала координат оси OY). Подчеркнем, что физический смысл имеет изменение потенциальной энергии при перемещении тел друг относительно друга. При любом выборе нулевого уровня изменение потенциальной энергии будет одинаковым.
При расчете движения тел в поле гравитации Земли, но на значительных расстояниях от нее, во внимание нужно принимать закон всемирного тяготения (зависимость силы тяготения от расстояния до цента Земли). Приведем формулу, выражающую зависимость потенциальной энергии тела.
Здесь G — гравитационная постоянная, M — масса Земли.
Потенциальная энергия пружины
Представим, что в первом случае мы взяли пружину и удлинили ее на величину x . Во втором случае мы сначала удлинили пружину на 2 x , а затем уменьшили на x . В обоих случаях пружина оказалась растянута на x , но это было сделано разными способами.
При этом работа силы упругости при изменении длины пружины на x в обоих случаях была одинакова и равна
A у п р = — A = — k x 2 2 .
Величина E у п р = k x 2 2 называется потенциальной энергией сжатой пружины. Она равна работе силы упругости при переходе из данного состояния тела в состояние с нулевой деформацией.
5 1 Кинетическая энергия твердого тела при поступательном движении
| Назва | 5 1 Кинетическая энергия твердого тела при поступательном движении |
| Дата конвертації | 04.10.2013 |
| Розмір | 159.26 Kb. |
| Тип | Лекция |
mir.zavantag.com > Математика > Лекция
5.3 Кинетическая энергия твердого тела Получим выражения для кинетической энергии твердого тела, которое совершает поступательное движение, вращение вокруг неподвижной оси и плоское движение Кинетическая энергия тела равна сумме кинетических энергий всех материальных точек, на которые это тело разбито:
Если тело движется поступательно, то скорость каждой его точки i одинакова и равна скорости движения центра масс, С. Тогда формула (5.16) для кинетической энергии поступательного движения примет вид:
где ^ 5.3.2 Кинетическая энергия твердого тела вращающегося вокруг неподвижной оси
где Iz момент инерции тела относительно оси вращения. Таким образом, кинетическая энергия твердого тела вращающегося вокруг неподвижной оси, пропорциональна квадрату угловой скорости.
где ω – угловая скорость. Согласно (5.13)
Если Mz и dφ имеют одинаковые знаки, то δA >0; если же их знаки противоположны, то δA ^ 5.3.4 Кинетическая энергия при поступательно-вращательном движении где ^ 1с — момент инерции тела относительно оси вращения, проходящей через его центр масс,ω — угловая скорость тела, m — его масса, υС – скорость движения центра масс. ^ Кинетическая энергия твердого тела при плоском движении складывается из энергии вращения в системе центра масс и энергии движения центра масс. Пример 5.3 Найти кинетическую энергию однородного цилиндра с массой m, катящегося без скольжения с постоянной скоростью υ. Используем формулу (5.22), в которую подставим IC=mR 2 /2 – момент инерции цилиндра относительно оси, проходящей через его центр масс, и υС = υ = ωR:
Течение жидкостей и газов. Ламинарный и турбулентный Раздел физики, в котором рассматривают законы равновесия и движения жидких и газообразных сред, а также их взаимодействия с твердыми телами, называют гидроаэромеханикой. ^ Внешнее давление, производимое на жидкость или газ, передается ими во все стороны равномерно (закон Паскаля). Наглядно течение жидкости изображается линиями тока, которые проводят так, что касательные к ним совпадают по направлению с векторами скоростей жидкости в соответствующих точках пространства. Поверхность, которая образована линиями тока, проведенными через все точки малого замкнутого контура, называют трубкой тока. Часть жидкости, ограниченную трубкой тока, называют струей. ^ В реальных жидкостях между отдельными слоями потока действует внутреннее (вязкое) трение. Причиной внутреннего трения является перенос молекулами импульса из одного слоя в другой. Жидкость, в которой отсутствует внутреннее трение, называют идеальной жидкостью. ^ Наблюдается два вида течения жидкости (или газа) — ламинарное и турбулентное. При ламинарном (слоистом) течении каждый выделенный слой скользит относительно соседних слоев, не перемешиваясь с ними. Ламинарное течение является стационарным и характеризуется постоянным во времени распределением поля скоростей по объему жидкости. ^ Турбулентное (вихревое) течение жидкости возникает когда вдоль потока происходит интенсивное вихреобразование и перемешивание жидкости. При этом режиме течения частицы жидкости приобретают составляющие скоростей, перпендикулярные течению. ^ Установлено, что характер течения зависит от значения числа Рейнольдса: где Рассмотрим трубку тока с сечениями dS1 и dS2 (рис.6.1) скорости жидкости в этих сечениях обозначим через υ1 и υ2, а плотность жидкости – соответственно ρ1 и ρ2. Масса жидкости
где dmсек – секундный массовый расход жидкости вдоль струи. Так как сечения были выбраны произвольно, то :
Соотношение (6.2) называется уравнением неразрывности.
В случае несжимаемой жидкости плотность одинакова во всех сечениях трубки тока и уравнение неразрывности имеет вид:
Если плотность жидкости и скорость постоянны по всему поперечному сечению S, то
Выделим объем жидкости, которая в некоторый момент времени t заполняет участок, ограниченный сечениями S1 и ^ S2 (рис. 6.2). Давление в сечении S1 равно P1 , а в сечении S2 — P2 . Если течение стационарное, то объем жидкости к моменту времени t+Δt переместится и будет заключен между сечениями Определим изменение полной механической энергии за малый промежуток времени t. За это время масса жидкости, заключенная между сечениями S1 и где T – кинетическая энергия выделенного объема жидкости, U — потенциальная энергия этого объема. Втекающая в выделенный объем и вытекающая из этого объема массы жидкости m равны, поэтому формулу (6.4) можно переписать через массу:
Где υ2 и υ1 – скорости объема в сечениях S2 и S1 , h1 и h2 – высота сечений S1 и S2 относительно некоторого уровня, соответственно. Изменение полной механической энергии равно работе A внешних сил по перемещению массы m На данный объем жидкости Сила ^ F1 совершает работу A 1 по перемещению втекающей массы на пути При перемещении вытекающей массы совершается работа A2 против силы F2 на пути 2 t. Работа сил давления, приложенных к боковой поверхности трубки тока, равна нулю, так как эти силы направлены перпендикулярно к направлению течения жидкости. Приравнивая (6.4) и (6.5), получим
Выразив Δm через плотность (Δm = V), получим
Поскольку сечения S1 и S2 выбраны произвольно, то в общем случае можно записать: Соотношение (6.6) представляет собой уравнение Бернулли. Для горизонтальной трубки тока уравнение Бернулли имеет вид При отсутствии течения (υ=0) из (6.7)получим p = const. Это давление в выражениях (6.6) и (6.7) p называют статическим. Величина 2 /2 — динамическое давление, gh ‑ гидростатическое давление. Можно показать, что в случае установившегося течения константа в правой части уравнения (6.6) одинакова для всех трубок тока, т. е. что уравнение Бернулли справедливо для всего потока. ограниченного стенками трубы. Из уравнений Бернулли и неразрывности следует, что в местах сужения трубопровода (или уменьшения сечения трубки тока) скорость течения жидкости возрастает, а давление понижается.
Для двух сечений 1‑1 и 2‑2 запишем уравнение Бернулли
Из уравнения неразрывности
где S1 и S2 ‑ площади поперечных сечений сосуда и отверстия. Поскольку S1 >> S2 , то членом Полученное уравнение имеет название формулы Торричелли. Из нее видно, что частицы жидкости, выходя из отверстия, имеют такую же скорость, какую они приобрели бы, свободно падая с высоты Н. ^ Течение вязких жидкостей и газов в трубах. Формула Пуазейля Рассмотрим течение жидкости вблизи плоской поверхности (рис.6.3). В направлении, перпендикулярном оси ^ X, скорость движения во всех точках одинакова. Это значит, что скорость υ является функцией только х. Как показывает опыт, импульс P, переносимый в единицу времени через единицу площади сечения, перпендикулярного оси X, определяется уравнением
где Вязкость проявляется в том, что любой слой газа или жидкости, движущийся относительно соседнего, испытывает действие некоторой силы. Эта сила и представляет собой силу трения между слоями газа. Уравнение (6.10) следует поэтому записать в виде
Выражение (6.11) — закон Ньютона для вязкого течения жидкости или газа. Коэффициент динамической вязкости согласно (6.11) численно равен силе трения между слоями площадью 1 м 2 при величине градиента скорости (в направлении, перпендикулярном к слоям), равном единице (1 м/сек на 1 м длины). Размерность в СИ []= Па · с (паскаль-секунда). В случае стационарного ламинарного течения жидкости по трубке небольшого радиуса ^ R объем жидкости, протекший за секунду через сечение трубки прямо пропорционален разности давлений p 1 и p2 у входа в трубку и на выходе из нее, четвертой степени радиуса R трубки и обратно пропорционален длине l трубки и коэффициенту вязкости
где Vсек – секундный расход жидкости. Соотношение (6.12) представляет собой формулу Пуазейля. Формула Пуазейля используется для определения коэффициента динамической вязкости сред η путем измерения объема V вытекающей жидкости за некоторое время t при заданном перепаде давлений. Этот метод называется вискозиметрическим. Пример 6.2. Вывод формулы Пуазейля с помощью закона Ньютона для вязкого трения Выделим объем жидкости или газа в виде цилиндра длиной l и радиусом r. При стационарном течении с постоянной скоростью сумма всех сил, действующих на выделенный объем, равна нулю. На данный объем действуют сила вязкого трения Fтр, , которая уравновешивается силой Fд, возникающей из-за перепада давления на длине трубки (рис. 6.4).
Сила Fтр, действует вдоль поверхности выделенного цилиндра с площадью S = 2lr и согласно закону Ньютона (6.11) равна
Так как Fтр,по модулю равна силе Fд, то приравнивая два последних выражения, получим
Разделяя переменные и интегрируя это уравнение, получим распределение скорости течения в радиальном направлении:
Постоянную С определим из условия равенства нулю скорости на стенке трубы:
С учетом последнего равенства:
Объем жидкости dV, протекший за секунду через кольцевое сечение шириной dr (рис. 5-4), с учетом (6.14) равен:
Интегрирование последнего соотношения в пределах от 0 до R приводит к формуле (6.12). ^ 6.4 Движение тел в жидкостях и газах
Силу На рис. 5-5 показан вид линий тока идеальной жидкости, обтекающей длинный круговой цилиндр, ось которого расположена перпендикулярно к плоскости чертежа. Скорость жидкости отлична от нуля во всех точках поверхности цилиндра, за исключением критических точек а и b, в которых она равна нулю. На участках ас и ad скорость жидкости возрастает, а статическое давление убывает в соответствии с уравнением Бернулли. В точках с и d скорость максимальна, а давление минимально. На участках cb и db скорость убывает, а давление возрастает. Линии тока симметричны относительно плоскостей аb и cd. Поэтому результирующая всех элементарных сил давления жидкости на цилиндр равна нулю. Так как жидкость идеальная, то нет и сил трения, т. е.
Сила лобового сопротивления тела, обтекаемого реальной жидкостью, всегда отлична от нуля. В вязкой жидкости возникает сила лобового сопротивления Сила лобового сопротивления, действующей на небольшой шарик, движущийся в вязкой жидкости с малой скоростью, определяется законом Стокса:
где η — коэффициент динамической вязкости жидкости, υ — скорость ‘шара, а r — его радиус. Соотношение (6.14) справедливо при малых значениях числа Рейнольдса Re = ρυd/η источники: http://zaochnik.com/spravochnik/fizika/zakony-sohranenija-v-mehanike/kineticheskaja-i-potentsialnaja-energii/ http://mir.zavantag.com/matematika/41913/index.html |
. (5.16)
, (5.17)
— масса тела.
, то линейная скорость i-ой точки равна I = ri , где ri расстояние от этой точки до оси вращения. Поэтому, из (4.17) следует:
, (5.18)
,
. Подставив это выражение в последнее уравнение для δA и учитывая, что 
, получим
. (5.19)
, (5.22)
.
плотность жидкости (газа), 
средняя по сечению трубы скорость жидкости, l характерный размер канала (например, диаметр трубы), 
коэффициент динамической вязкости. Переход от ламинарного течения к турбулентному происходит при Re> Reкр. Например, значение критического числа Reкр для гладких цилиндрических труб составляет примерно 2300.
, поступившей через сечение dS1 за единицу времени, будет равна массе жидкости
, которая вытекла за единицу времени через сечение dS2.:
,
. (6.2)
. (6.3)
и 
. Промежуток Δt выберем настолько малым, что скорости течения жидкости в пределах объема трубки тока, ограниченного сечениями S1 и 
, (6.4)
действуют силы F1 = p1 S1 в сечении S1 , F2 = p2 S2 в сечении S2 и силы давления, приложенные к боковой поверхности трубки тока.
.
.
.
.
. (6.8)
,
в левой части уравнения (6.8) можно пренебречь. Тогда
и 
. (6.9)
, (6.10)
— градиент скорости вдоль оси X, характеризующий быстроту изменения скорости вдоль этой оси (изменение скорости на каждую единицу длины). Знак минус означает, что импульс переносится в направлении уменьшения скорости. Коэффициент — коэффициент динамической вязкости, который зависит от свойств газа или жидкости.
, (6.11)
, (6.12)
. (6.13)
.
.
.
. (6.14)
.
, действующая на тело со стороны встречного потока жидкости, равна векторной сумме равнодействующих сил давления, 
, и сил трения, 
, приложенных к поверхности тела:
.
, противоположную по направлению вектора скорости тела, и подъемную силу, направленную перпендикулярно этой скорости. Эти силы зависят от скорости потока, формы тела, его размеров, а также от свойств жидкости. Если жидкость идеальная, то, как показывают расчеты, сила лобового сопротивления тела равна нулю, т.е. в идеальной жидкости тело должно двигаться без всякого сопротивления.
, которая равна векторной сумме силы сопротивления трения и силы сопротивления давления. Сила сопротивления трения есть результирующая сил трения, действующих на все малые элементы поверхности тела. Сила сопротивления давления обусловлена тем, что из-за торможения жидкости, происходящего в пограничном слое, давление жидкости на лобовую часть поверхности тела не равно давлению на заднюю часть тела.
, (6.15)