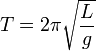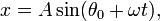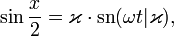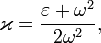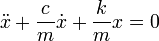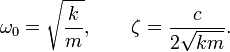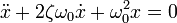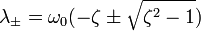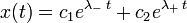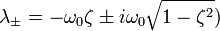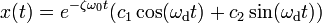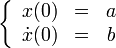Уравнение колебаний маятника
Рис.1
Исследуем выражение (2) в зависимости от разности фаз (φ2 — φ1):
1) φ2 — φ1 = ±2mπ (m = 0, 1, 2, . ), тогда A=A1+A2, т. е. амплитуда результирующего колебания А будет равна сумме амплитуд складываемых колебаний;
2) φ2 — φ1 = ±(2m+1)π (m = 0, 1, 2, . ), тогда A=|A1–A2|, т. е. амплитуда результирующего колебания будет равна разности амплитуд складываемых колебаний.
Для практики представляет особый интерес случай, когда два складываемых гармонических колебания одинакового направления мало отличаются по частоте. После сложения этих колебаний получаются колебания с периодически изменяющейся амплитудой. Периодические изменения амплитуды колебания, которые возникают при сложении двух гармонических колебаний с близкими частотами, называются биениями.
Пусть амплитуды складываемых колебаний равны А, а частоты равны ω и ω+Δω, причем Δω
23 Колебания физического маятника.
Физический маятник — осциллятор, представляющий собой твёрдое тело, совершающее колебания в поле каких-либо сил относительно точки, не являющейся центром масс этого тела, или неподвижной оси, перпендикулярной направлению действия сил и не проходящей через центр масс этого тела.
Определения
— угол отклонения маятника от равновесия;
— начальный угол отклонения маятника;
— масса маятника;
— расстояние от точки подвеса до центра тяжести маятника;
— радиус инерции относительно оси, проходящей через центр тяжести.
— ускорение свободного падения.
Момент инерции относительно оси, проходящей через точку подвеса:

[править] Дифференциальное уравнение движения физического маятника
Основная статья: Приведённая длина
Пренебрегая сопротивлением среды, дифференциальное уравнение колебаний физического маятника в поле силы тяжести записывается следующим образом:
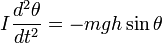
Полагая 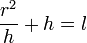
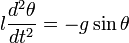
Последнее уравнение аналогично уравнению колебаний математического маятника длиной 

[править] Центр качания физического маятника
Центр качания — точка, в которой надо сосредоточить всю массу физического маятника, чтобы его период колебаний не изменился.
Поместим на луче, проходящем от точки подвеса через центр тяжести точку на расстоянии 
Действительно, если всю массу сосредоточить в центре качания, то центр качания будет совпадать с центром масс. Тогда момент инерции относительно оси подвеса будет равен 
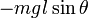
[править] Теорема Гюйгенса
[править] Формулировка
Если физический маятник подвесить за центр качания, то его период колебаний не изменится, а прежняя точка подвеса сделается новым центром качания.
[править] Доказательство
Вычислим приведенную длину для нового маятника:
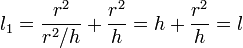
Совпадение приведённых длин для двух случаев и доказывает утверждение, сделанное в теореме.
[править] Период колебаний физического маятника
Для того, чтобы найти период колебаний физического маятника, необходимо решить уравнение качания. Для этого умножим левую часть этого уравнения на 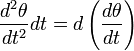
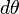
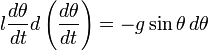
Интегрируя это уравнение, получаем.
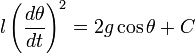
где 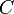
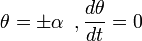
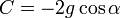
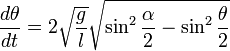
Отделяем переменные и интегрируем это уравнение:
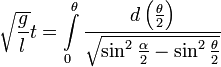
Удобно сделать замену переменной, полагая 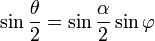
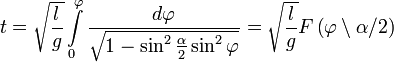
Здесь 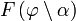
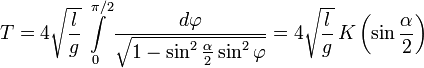
Здесь 
[править] Период малых колебаний физического маятника
Если амплитуда колебаний 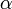
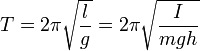
24 Колебания математического маятника
Математи́ческий ма́ятник — осциллятор, представляющий собой механическую систему, состоящую из материальной точки, находящейся на невесомой нерастяжимой нити или на невесомом стержне в однородном поле сил тяготения. Период малых собственных колебаний математического маятника длины l неподвижно подвешенного в однородном поле тяжести с ускорением свободного падения g равен
и не зависит [1] от амплитуды и массы маятника.
Плоский математический маятник со стержнем — система с одной степенью свободы. Если же стержень заменить на растяжимую нить, то это система с двумя степенями свободы со связью. Пример школьной задачи, в которой важен переход от одной к двум степеням свободы.
При малых колебаниях физический маятник колеблется так же, как математический с приведённой длиной.
Уравнение колебаний маятника
Колебания математического маятника описываются обыкновенным дифференциальным уравнением вида
где ω ― положительная константа, определяемая исключительно из параметров маятника. Неизвестная функция x(t) ― это угол отклонения маятника в момент t от нижнего положения равновесия, выраженный в радианах; 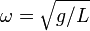
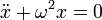
[править] Решения уравнения движения
[править] Гармонические колебания
Маятник, совершающий малые колебания, движется по синусоиде. Поскольку уравнение движения является обыкновенным ДУ второго порядка, для определения закона движения маятника необходимо задать два начальных условия — координату и скорость, из которых определяются две независимых константы:
где A — амплитуда колебаний маятника, θ0 — начальная фаза колебаний, ω — циклическая частота, которая определяется из уравнения движения. Движение, совершаемое маятником, называется гармоническими колебаниями
[править] Нелинейный маятник
Для маятника, совершающего колебания с большой амплитудой, закон движения более сложен:
где 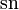

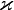
Параметр 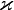
где 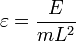
Период колебаний нелинейного маятника
где K — эллиптический интеграл первого рода.
[править] Движение по сепаратрисе
Движение маятника по сепаратрисе является непериодическим. В бесконечно далёкий момент времени он начинает падать из крайнего верхнего положения в какую-то сторону с нулевой скоростью, постепенно набирает её, и останавливается, возвратившись в исходное положение.
25 Затухающие колебания. Зависимость амплитуды от времени.
Затухающие колебания — колебания, энергия которых уменьшается с течением времени. Бесконечно длящийся процесс вида 
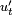
Пускай имеется система, состоящая из пружины (подчиняющейся закону Гука), один конец которой жёстко закреплён, а на другом находится тело массой m. Колебания совершаются в среде, где сила сопротивления пропорциональна скорости с коэффициентом c (см. вязкое трение).
Тогда второй закон Ньютона для рассматриваемой системы запишется так:
где Fc — сила сопротивления, Fy — сила упругости
или в дифференциальной форме
где k — коэффициент упругости в законе Гука, c — коэффициент сопротивления, устанавливающий соотношение между скоростью движения грузика и возникающей при этом силой сопротивления.
Для упрощения вводятся следующие обозначения:
Величину ω называют собственной частотой системы, ζ — коэффициентом затухания.
Тогда дифференциальное уравнение принимает вид
Сделав замену x = e λt , получают характеристическое уравнение
Корни которого вычисляются по следующей формуле
[править] Решения
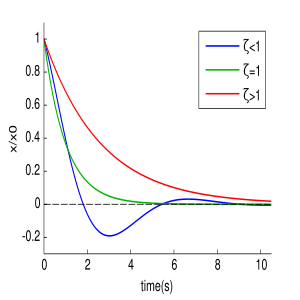
Зависимость графиков колебаний от значения ζ.
В зависимости от величины коэффициента затухания решение разделяется на три возможных варианта.
Если 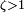
В этом случае колебания с самого начала экспоненциально затухают.
- Граница апериодичности
Если 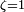
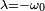
В данном случае может иметь место вре́менный рост, но потом — экспоненциальное затухание.
Если 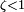
Тогда решением исходного дифференциального уравнения является
Где 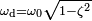
Константы c1 и c2 в каждом из случаев определяются из начальных условий:
26 Вынужденные колебания. Понятие резонанса.
Вынужденные колебания — колебания, происходящие под воздействием внешних сил, меняющихся во времени.
Автоколебания отличаются от вынужденных колебаний тем, что последние вызваны периодическим внешним воздействием и происходят с частотой этого воздействия, в то время как возникновение автоколебаний и их частота определяются внутренними свойствами самой автоколебательной системы.
Наиболее простой и содержательный пример вынужденных колебаний можно получить из рассмотрения гармонического осциллятора и вынуждающей силы, которая изменяется по закону: 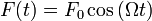
Электронная библиотека
Пример 1. Материальная точка массой m = 10 г совершает гармонические колебания с частотой n = 0,2 Гц. Амплитуда колебаний равна 5 см. Определить: 1) максимальную силу, действующую на точку; 2) полную энергию колеблющейся точки.
Дано: m = 10 г = 10 -2 кг; n = 0,2 Гц; А = 5 см = 5×10 -2 м.
Решение. Уравнение гармонического колебания имеет вид:
Тогда скорость и ускорение колеблющейся точки равна:
Согласно второму закону Ньютона сила, действующая на точку, равна:
при , поэтому максимальное искомое значение силы:
Полная энергия колеблющейся точки равна:
Подставив сюда , найдем искомую полную энергию:
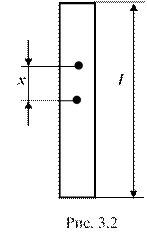
Пример 2. Физический маятник представляет собой тонкий однородный стержень.
Определить длину стержня (l), если частота колебаний маятника максимальна, когда точка подвеса О находится от центра масс С на расстоянии 20,2 см (рис. 3.2).
Дано: х = 20,2 см = 0,202 м; .
Решение. Циклическая частота колебаний физического маятника равна:
где m – масса маятника; J – момент его инерции.
Согласно теореме Штейнера, момент инерции стержня относительно точки подвеса, отстоящей от центра масс на расстоянии х, равен:
Подставив (2) в (1), получим:
Найдем экстремум функции (3):
т.е. искомая длина маятника равна:
Вычисляя, получим: l = 70 см.
Срочно?
Закажи у профессионала, через форму заявки
8 (800) 100-77-13 с 7.00 до 22.00
Лабораторная работа № 5
Лабораторная работа № 5
изучение закона колебаний
5.1. Цель работы: Экспериментальная проверка закона колебаний физического маятника при малой угловой амплитуде. Освоить метод определения ускорения силы тяжести с помощью физического маятника.
5.2. Краткое теоретическое введение
5.2.1. Период колебаний физического маятника
Физическим маятником называется твердое тело произвольной формы, укрепленное на неподвижной горизонтальной оси (не проходящей через его центр масс) и способное совершать колебания относительно этой оси.
В состоянии устойчивого равновесия физического маятника линия, проходящая через точки подвеса «О» и центра масс «С», направлена вертикально (см. рис.5.1).
Если маятник отклонить от положения равновесия на некоторый угол a и отпустить, то он будет совершать колебательное движение (рис.5.1) под действием момента силы тяжести относительно оси вращения. Проекция на ось вращения момента силы тяжести равна:

где m – масса маятника,
g – ускорение свободного падения,
a – расстояние от точки подвеса «О» до центра масс «С».
Уравнение движения (уравнение моментов) физического маятника в проекции на ось вращения имеет следующий вид (см. Приложение):

где I – момент инерции маятника относительно оси вращения.
Если угол отклонения достаточно мал (a ;
4) периода Ti колебаний;
Число необходимых измерений – 25.
· Перемещая призму подвеса последовательно на одну проточку(10мм), двигаясь к центру масс, проведите измерения времени 10 периодов колебаний маятника по 3 раза для каждого положения призмы подвеса. Занести результаты в таблицу. Кронштейн (5) также надо перемещать вверх так, чтобы нижний конец стержня пересекал луч фотодатчика.
5.5. Математическая обработка результатов измерений
5.5.1. По средним значениям определить период колебаний Ti и занести эти значения в таблицу.
5.5.2. Построить график зависимости периода колебаний Тi от расстояния между точкой подвеса и центром масс аi, используя все экспериментальные точки.
5.5.3. Построить в более крупном масштабе (увеличив масштаб Т в 20¸50 раз) отдельно область зависимости Т=f(а), в которой одному и тому же периоду Тi отвечают два значения величины аi.
5.5.4. Проведя 5-6 горизонтальные прямые, найти значения а1i и a2i, соответствующие точкам пересечения этих прямых с графиком Т=f(а) и определить приведённые длины l0i=a1i+a2i для каждого значения Ti.
5.5.5. Подставив полученные значения l0i и Ti в формулу (5.15), найти экспериментальные значения ускорения свободного падения.
5.5.6. Определить среднее значение и доверительный интервал Dg по методу прямых измерений для заданного значения доверительной вероятности.
5.5.7. Сравниваем полученное значение с табличным значением для города Алматы (g=9,804 м/с2).
5.5.8. Используя формулу для момента инерции тонкого стержня относительно оси вращения, перпендикулярной стержню, проходящей через центр масс:
(где m — масса стержня, а l — его длина), рассчитать по формулам (5.14) теоретическое значение минимального периода колебаний Tmin и соответствующее ему расстояние а* от точки подвеса до центра масс; сравнить их с полученными экспериментально по графику.
5.6. Вопросы для самоконтроля
5.6.1. Дайте определение физического и математического маятников.
5.6.2. Как выглядят кривые зависимости периода колебаний от расстояния а между точкой подвеса и центром масс для математического и физического маятников, изображенных на одном и том же графике? Объясните, почему именно так?
5.6.3. Остается ли момент инерции физического маятника одинаковым относительно осей, проходящих через разные точки подвеса? Почему?
5.6.4. Каков физический смысл термина «приведенная длина физического маятника»?
5.6.5. Каким образом может влиять масса и форма подвеса маятника на его движение? Приведет ли учет наличия подвеса к увеличению или уменьшению периода колебаний?
5.6.6. Объясните, почему кривая зависимости периода T колебаний от величины а на рис.5.2. симметрична относительно центра масс, хотя сам физический маятник такой симметрией может и не обладать?
5.7.1. Ñèâóõèí Ä.Â. Îáùèé êóðñ ôèçèêè, Ò.1.-Ì.: Íàóêà, 1974.
5.7.2. Ãîëüäèí Ë.Ë. Ðóêîâîäñòâî ê ëàáîðàòîðíûì çàíÿòèÿì ïî ôèçèêå. -Ì.: Íàóêà, 1973.
П Р И Л О Ж Е Н И Е
Основным уравнением движения твердого тела, закрепленного в точке, в частности способного совершать лишь вращение вокруг неподвижной оси, является уравнение моментов:

где 

Для тела, вращающегося вокруг неподвижной оси, имеем:

где I— момент инерции тела относительно оси вращения;

Поэтому, подставляя (П2) в (П1), получим основное уравнение вращательного движения в следующем виде:

Принимая во внимание, что по определению 

Существует лишь одна сила (если пренебречь трением), создающая момент относительно оси вращения — это сила тяжести, приложенная к центру масс, поэтому

где 


Проекция М вектора 

Знак «минус» в выражении (П.5) показывает, что эта проекция направлена против выбранного направления углового перемещения при отклонении от положения равновесия.
Таким образом, уравнение (П.3), записанное в проекции на ось вращения примет вид:
или в других обозначениях

где 

Уравнение (П6) описывает колебания физического маятника вокруг неподвижной оси вращения.
http://libraryno.ru/3-1-10-primery-resheniya-zadach-2013_fiz_electro/
http://pandia.ru/text/80/315/303.php
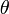 — угол отклонения маятника от равновесия;
— угол отклонения маятника от равновесия; — масса маятника;
— масса маятника;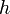 — расстояние от точки подвеса до центра тяжести маятника;
— расстояние от точки подвеса до центра тяжести маятника; — радиус инерции относительно оси, проходящей через центр тяжести.
— радиус инерции относительно оси, проходящей через центр тяжести.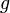 — ускорение свободного падения.
— ускорение свободного падения.