Спец главы математики колебания мембраны матлаб. СГМ — Лаб_3_Почапская_Евгения_ВИАС22. Лабораторная работа 3 по дисциплине Специальные главы математики Вариант 18 Студент Почапская Е. А. Группа виас22 Проверил
| Название | Лабораторная работа 3 по дисциплине Специальные главы математики Вариант 18 Студент Почапская Е. А. Группа виас22 Проверил |
| Анкор | Спец главы математики колебания мембраны матлаб |
| Дата | 26.10.2021 |
| Размер | 499.5 Kb. |
| Формат файла |  |
| Имя файла | СГМ — Лаб_3_Почапская_Евгения_ВИАС22.docx |
| Тип | Лабораторная работа #256689 |
 С этим файлом связано 1 файл(ов). Среди них: ОС Почапская лаба 4.doc. С этим файлом связано 1 файл(ов). Среди них: ОС Почапская лаба 4.doc.  Показать все связанные файлы Подборка по базе: Практическая работа № 2.docx, Практические работа 6.docx, Практическая работа 1.docx, Самостоятельная работа 4-2. История.docx, Практическая работа 10.docx, Самостоятельная работа 4-3. История.docx, Лабораторная работа 1..docx, Контрольная работа по экономике 5 курс.doc, Лабораторная работа №2 208.docx, Практическая работа по конституционному праву.docx Показать все связанные файлы Подборка по базе: Практическая работа № 2.docx, Практические работа 6.docx, Практическая работа 1.docx, Самостоятельная работа 4-2. История.docx, Практическая работа 10.docx, Самостоятельная работа 4-3. История.docx, Лабораторная работа 1..docx, Контрольная работа по экономике 5 курс.doc, Лабораторная работа №2 208.docx, Практическая работа по конституционному праву.docx Федеральное государственное бюджетное образовательное учреждение «ДОНСКОЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ» Кафедра «Информационные технологи» Выполнила: Лабораторная работа № 3 Тема: Уравнение колебаний мембраныЦель работы: Изучение инструмента pdetool, получение навыков решения задач математической физики методом конечных элементов. Решение в среде MatLab. 1) Задаем область 3) Введем краевые условия 4) Введем начальные условия и промежуток времени. Для этого в окне PDE Modeler выбираем меню «Solve — Parameters…» и в строке Time вводим 0:5; в строке u(t0): вводим формулу -sin((pi*x)/3).*y*(y–2); в строке u’(t0): вводим 0. 5) Введем сеточную область. Разобъем область на треугольные элементы. После выберем меню «Plot — Parameters…» и отметим флажки «Height(3-D plot», «Plot in x-y grid», «Shou mesh». Для построения нажимаем кнопку «Plot». Выполните эксперименты и ответьте на вопросы 1) Какие изменения надо внести в программу, чтобы колебания были долгими? 2) Какие изменения надо внести в программу, чтобы получить нулевое решение (мембрана находится в покое)? 3) Какие изменения надо внести в программу, чтобы амплитуда колебаний была больше? 4) Какие изменения надо внести в программу, чтобы амплитуда колебаний была меньше? 5) Какие изменения надо внести в программу, чтобы получить свободные колебания? Колебания круглой мембраны По этой ссылке вы найдёте полный курс лекций по математике: Метод Фурье разделения переменных применяется также при изучении колебаний ограниченных тел, плоских или объемных. Рассмотрим в качестве примера задачу о свободных колебаниях под действием начальных возмущений однородной круглой мембраны радиуса г о с центром в начале координат, закрепленной по краю. Уравнение колебаний мембраны имеет вид Введем полярные координаты г, (р. Тогда отклонение точек мембраны будет функцией полярных координат г, и времени ). Пользуясь выражением для оператора Лапласа в полярных координатах, запишем уравнение колебаний мембраны в сле/ующем виде: Колебания круглой мембраны (мембрана закреплена по краю) и начальным условиям Таким образом, задача о колебаниях мембраны ставится так: найти фу нкцию ti(r, удовлетворяющую уравнению граничным условиям. Ограничимся важным частным случаем осесимметричных колебаний, когда начальные функции f nF не зависят от Ясно, что тогда в любой момент времени t > О величина отклонения мембраны не будет зависеть от полярного угла а будет только функцией г и t, и = u(r, t). Это означает, что при любом фиксированном t форма колеблющейся мембраны будет описываться поверхностью вращения. При этом предположении задача сводится к отысканию решения ti(r, t) уравнения (4) при граничном условии (5) и начальныхусловиях ди I Применяя метод разделения переменных, будем искать нетривиальные решения уравнения (4),удовлетворяющие граничному условию (5), в виде Подставляя функцию «(г, t) в форме (7) в уравнение (4) и разделяя переменные, получим Равенства (8) приводят к двум обыкновенным дифференциальным уравнениям (условие выражает естественное требование ограниченности решения u(r, t) в центре мембраны, т. е. при г = 0).
Итак, мы пришли к задаче на собственные значения: найти те значения параметра А, при которых существуют нетривиальные решения задачи (10)—(11), и отыскать эти решения. Запишем уравнение (10) в следующем виде: Это дифференциальное уравнение Бесселя с v = 0. Его общее решение . Из условия |+оо следует, что Сг = 0 (функция Неймана . Возможно вам будут полезны данные страницы: Таким образом, Граничное условие Д(г0) = 0 дает откуда следует, что число л/Аго должно быть одним из нулей функции Бесселя т.е. где Рк — нуль функции Jo имеет вид Колебания круглой мембраны Функция будет решением уравнения (4), удовлетворяющим граничному условию (5). Она определяет стоячие осесимметричные вол ны круглой мембраны. Решение исходной задачи (4)-(6) ищем в виде формального ряда (12) коэффициенты Ап и Вп которого определяются из начальных условий т.е. мы приходим к разложению данных функций /r) в ряды по функциям Бесселя. Нетрудно проверить, что при т ф п функции Jr) ортогональны на [0, го] с весом г. Известно, что всякая функция Ф(, удовлетворяющая граничным условиям задачи, может быть разложена в абсолютно и равномерно сходящийся ряд Фурье—Бесселя Колебания круглой мембраны Пользуясь этим, при достаточно гладких начальных условиях /(г) и F(r) получаем для коэффициентов Фурье—Бесселя функций /(г) и F(r) сле/^гощие формулы: Подставим найденные значения An и Bn в формулу (12). Если при этом ряд (12) сходится равномерно, так же как и ряды, получаемые из него двукратным почленным дифференцированием по каждому из аргументов t и г, то мы получаем решение задачи (4)-(6). Присылайте задания в любое время дня и ночи в ➔ Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института. Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды. Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги. Дата добавления: 2013-12-23 ; просмотров: 3527 ; Нарушение авторских прав Б) Уравнение колебаний струны. Неявная схема А) Уравнение колебаний струны. Явная схема Рассмотрим задачу о малых колебаниях натянутой струны с распределенной по длине нагрузкой f(x, t) (рис. 8.1): utt(xi, tk)= uxx(xi, tk)= Обозначим через ui,k приближенные значения искомой (функции в точках (xi, tk). Тогда из уравнения (8.11) получим разностное уравнение (разностную схему), которое аппроксимирует уравнение (8.11) с порядком О(h 2 + τ 2 ): На рис. 8.2, б изображен шаблон «крест» разностного уравнения (8.16). Разностное уравнение (8.16) связывает значения неизвестной функции на трех слоях (k – 1, k, k + 1) Чтобы найти значения неизвестной функции на слое k = 1, используем условие для производной ut(x, 0) из (8.12). Для этого построим разложение в ряд Тейлора: u(xi, t1) = u(xi, τ) = u(xi, 0) + ut(хi, 0)τ + Из уравнения (8.11), учитывая первое условие в (8.12), выразим вторую производную Теперь, учитывая условие ut(x, 0) = μ0(x) в (8.12), из (8.18), (8.19) выводим формулу для вычисления значений функции на первом слое: u(xi, t1) = μ(xi) + μ0(xi)τ + С учетом (8.13) окончательно получим для приближенных значений искомой функции на первом слое формулы ui, 1 = μ(xi) + μ0(xi)τ + Учитывая граничные условия (8.13), из (8.16) выводим формулы для вычисления значений на слоях k = 2. М: ui, k = 2ui, k — 1 — ui, k — 2 + Таким образом, получены явные формулы (8.17), (8.21), (8.22) решения разностной задачи. Разностная схема называется устойчивой, если она имеет единственное решение и малым изменениям исходных данных отвечают малые изменения решения. Известен следующий факт: для выполнения условия устойчивости разностной схемы (8.16) необходимо и достаточно, чтобы выполнялось условие Куранта сτ 0 находим методом прогонки. 2.1. Вычислим правые части (8.26): 2.2. Вычислим прогоночные коэффициенты; Рассмотрим задачу для уравнения колебаний однородной прямоугольной мембраны: |
Не нашли то, что искали? Google вам в помощь!
http://natalibrilenova.ru/kolebaniya-krugloj-membranyi/
http://life-prog.ru/1_17684_raznostniy-metod-dlya-uravneniya-kolebaniy-membrani.html


 (1)
(1) (2)
(2) на границе области
на границе области  (условие Дирихле) (3)
(условие Дирихле) (3)























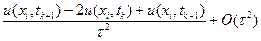
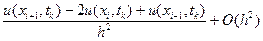
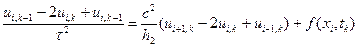




 На слое k = 0 заданы начальные условия (8.12), из которых следует, что
На слое k = 0 заданы начальные условия (8.12), из которых следует, что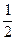 utt(xi, 0)τ 2 + O(τ 3 ). (8.18)
utt(xi, 0)τ 2 + O(τ 3 ). (8.18)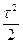 (с 2 μ»(хi) + f(хi, 0)) + О(τ 3 ). (8.20)
(с 2 μ»(хi) + f(хi, 0)) + О(τ 3 ). (8.20)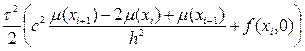
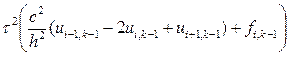
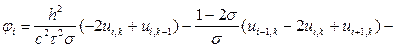
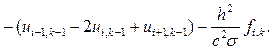 (8.29)
(8.29)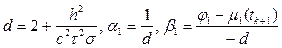 (8.30)
(8.30)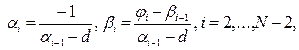 (8.31)
(8.31)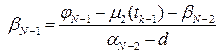 . (8.32)
. (8.32)