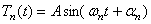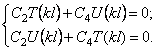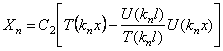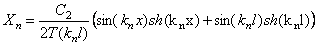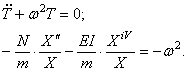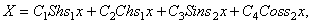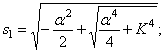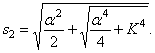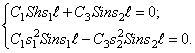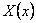Уравнение колебаний стержня с распределенной массой

Раздел 6. Свободные колебания систем с распределёнными параметрами

Основная особенность процесса свободных колебаний систем с бесконечным числом степеней свободы выражается в бесконечности числа собственных частот и форм колебаний. С этим связаны и особенности математического характера: вместо обыкновенных дифференциальных уравнений, описывающих колебания систем с конечным числом степеней свободы, здесь приходится иметь дело с дифференциальными уравнениями в частных производных. Кроме начальных условий, определяющих начальные смещения и скорости, необходимо учитывать и граничные условия, характеризующие закрепление системы.

6.1. Продольные колебания стержней

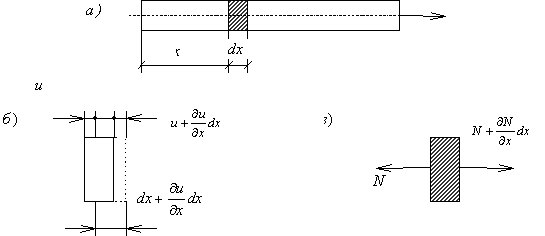
При анализе продольных колебаний прямолинейного стержня (рис.67,а) будем считать, что поперечные сечения остаются плоскими и что частицы стержня не совершают поперечных движений, а перемещаются только в продольном направлении.

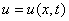
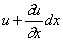
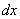
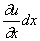
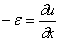
Пусть u — продольное перемещение текущего сечения стержня при колебаниях; это перемещение зависит от расположения сечения (координаты x ) и от времени t . Таким образом, есть функция двух переменных; её определение и представляет основную задачу. Перемещение бесконечно близкого сечения равно , следовательно, абсолютное удлинение бесконечно малого элемента равно (рис.67,б), а относительное его удлинение .

Соответственно продольная сила в сечении с координатой х может быть записана в виде

, (173)

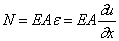
где 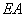жёсткость стержня при растяжении (сжатии). Сила N также является функцией двух аргументов – координаты х и времени t .

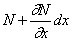
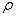
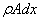
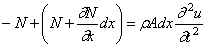
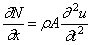
Рассмотрим элемент стержня, расположенный между двумя бесконечно близкими сечениями (рис.67,в). К левой грани элемента приложена сила N, а к правой – сила . Если обозначить через плотность материала стержня, то масса рассматриваемого элемента составляет . Поэтому уравнение движения в проекции на ось х

. (174)

Учитывая (173) и принимая A = const , получим

, (175)

. (176)

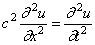
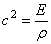
Следуя методу Фурье, ищем частное решение дифференциального уравнения (175) в виде

, (177)

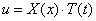
т.е. предположим, что перемещение u можно представить в виде произведения двух функций, одна из которых зависит только от аргумента х , а другая только от аргумента t . Тогда вместо определения функции двух переменных u ( x , t ) необходимо определять две функции X( x ) и T( t ), каждая из которых зависит только от одной переменной.

Подставив (177) в (174), получим

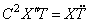
где штрихами обозначена операция дифференцирования по x , а точками – по t . Перепишем это уравнение таким образом:

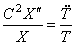
Здесь левая часть зависит только от x,а правая – только от t . Для тождественного выполнения этого равенства (при любых x и t ) необходимо, чтобы каждая из его частей была равна постоянной, которую обозначим через :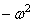

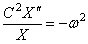
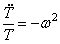
; . (178)

Отсюда следуют два уравнения:

; . (179)

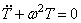
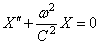
Первое уравнение имеет решение:

, (180)

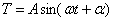
указывающее на колебательный характер, причём из (180) видно, что неизвестная величина 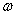имеет смысл частоты свободных колебаний.

Второе из уравнений (179) имеет решение:

, (181)

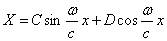
определяющее форму колебаний.

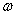
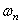
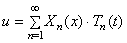
Частотное уравнение, определяющее величину , составляется путём использования граничных условий. Это уравнение всегда трансцендентное и имеет бесконечное число корней. Таким образом, число собственных частот бесконечно, причём каждому значению частоты соответствует своя функция T_n ( t ), определяемая зависимостью (180), и своя функция Xn ( x ), определяемая зависимостью (181). Решение (177) является лишь частным и не даёт полного описания движения. Полное решение получается путём наложения всех частных решений:

Функции X_n ( x ) называются собственными функциями задачи и описывают собственные формы колебаний. Они не зависят от начальных условий и удовлетворяют условию ортогональности, которое при А=const имеет вид

, если .

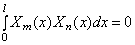
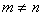
Рассмотрим некоторые варианты граничных условий.

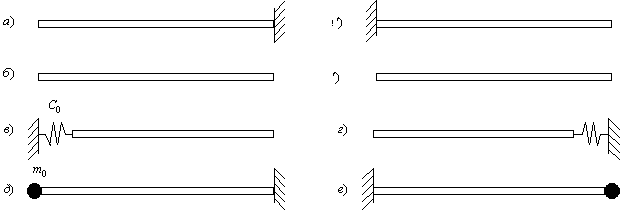
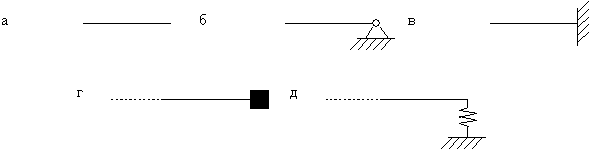
Закреплённый конец стержня (рис.68,а). В концевом сечении перемещение u должно быть равно нулю; отсюда следует, что в этом сечении

Свободный конец стержня (рис.68,б). В концевом сечении продольная сила

(183)

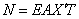
должна тождественно равняться нулю, что возможно, если в концевом сечении X’=0.

Упругозакреплённый конец стержня (рис.68,в).

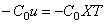
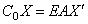
При перемещении u концевого стержня возникает упругая реакция опоры , где С_о — жёсткость опоры. Учитывая (183) для продольной силы, получим граничное условие

если опора расположена на левом конце стержня (рис.68,в), и

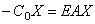
если опора расположена на правом конце стержня (рис.68,г).

Сосредоточенная масса 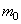на конце стержня.

Развиваемая массой сила инерции:

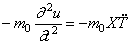
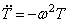
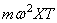
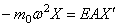
Так как, согласно первому из уравнений (179), , то сила инерции может быть записана в виде . Получаем граничное условие

если масса находится на левом конце (рис.68,д), и

, (184)

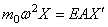
если масса связана с правым концом (рис.68,е).

Определим собственные частоты консольного стержня (рис.68,a’).

Согласно (182) и (183), граничные условия

X’=0 при х= .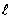

Подставляя поочерёдно эти условия в решение (181), получим

D=0; .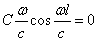

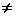
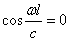
Условие С 0 приводит к частотному уравнению:

Корни этого уравнения

(n=1,2,…)

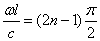
определяют собственные частоты:

(n=1,2,…). (185)

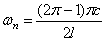
Первая (низшая) частота при n=1:

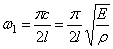
Вторая частота (при n=2):

и т. д.

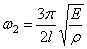
Определим собственные частоты стержня с массой 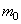на конце (рис.68,е).

Согласно (182) и (184), имеем

при х= .

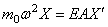
Подставляя эти условия в решение (181), получим:

D=0; .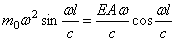

Следовательно, частотное уравнение при учёте (176) имеет вид

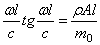
Здесь правая часть представляет собой отношение массы стержня к массе концевого груза.

Для решения полученного трансцендентного уравнения необходимо воспользоваться каким-либо приближённым способом.

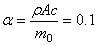
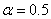
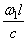
При и значения наиболее важного низшего корня будут соответственно 0.32 и 0.65 .

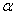
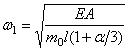
При малом отношении решающее влияние оказывает груз и хорошие результаты даёт приближённое решение

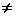
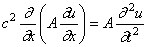
Для стержней переменного сечения, т.е. при А const , из (173) и (174) получается уравнение движения в виде

Это дифференциальное уравнение не поддаётся решению в замкнутом виде. Поэтому в подобных случаях приходится прибегать к приближённым методам определения собственных частот.

6.2. Крутильные колебания валов

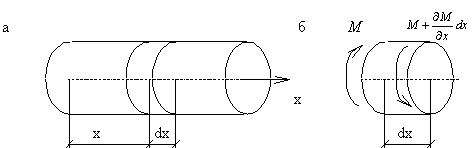
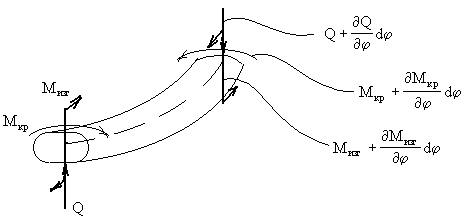
Крутильные колебания вала с непрерывно распределенной массой (рис.69,а) описываются уравнениями, которые по структуре полностью совпадают с приведенными выше уравнениями продольных колебаний стержней.

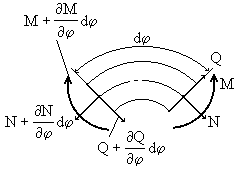
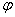
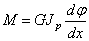
Крутящий момент М в сечении с абсциссой х связан с углом поворота дифференциальной зависимостью, аналогичной (173):

, (186)

где J_p-полярный момент инерции поперечного сечения.

В сечении, расположенном на расстоянии dx , крутящий момент равен (рис.69,б):

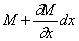
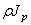
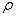
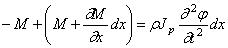
Обозначая через (где — плотность материала вала) интенсивность момента инерции массы вала относительно его оси (т.е. момент инерции единицы длины), уравнение движения элементарного участка вала можно записать так:

или подобно (174):

Подставляя сюда выражение (186), при Jp=const получим, аналогично (175):

, (187)

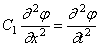
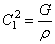
Общее решение уравнения (187), как и уравнения (175), имеет вид

(188)

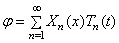
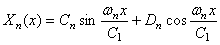
Собственные частоты и собственные функции при этом определяются конкретными граничными условиями.

В основных случаях закрепления концов аналогично случаю продольных колебаний получим

а) закрепленный конец ( 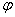=0): Х=0;

б) свободный конец (М=0): Х’=0;

в) упругозакрепленный левый конец: СоХ=GJpX ‘ ( Со-коэффициент жёсткости);

г) упругозакрепленный правый конец: — СоХ=GJpX ‘;

д ) диск на левом конце: 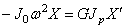(Jo-момент инерции диска относительно оси стержня);

е) диск на правом конце: .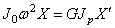

Если вал закреплён на левом конце (х=0), а правый конец ( х= ) свободен, то Х=0 при х=0 и Х’=0 при x= ; собственные частоты определяются аналогично (185):

(n=1,2,…).

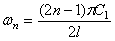
Если левый конец закреплён, а на правом конце имеется диск, получим трансцендентное уравнение:

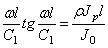
Если оба конца вала закреплены, то граничные условия будут X=0 при х=0 и х= . В этом случае из (188) получим

; D=0,

(n=1,2,…),

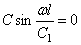
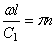
отсюда находим собственные частоты:

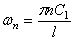
Если левый конец вала свободен, а на правом конце имеется диск, то X’=0 при х=0 ; Jo 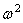X=GJpX ‘ при х= .

При помощи (188) находим

С=0; ,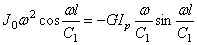

или трансцендентное частотное уравнение:

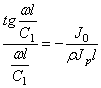
6.3.Изгибные колебания балок

6.3.1.Основное уравнение

Из курса сопротивления материалов известны дифференциальные зависимости при изгибе балок:

; (189)

, (190)

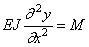
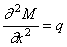
где EJ — жёсткость при изгибе; y=y ( x , t ) — прогиб; M=M( x , t ) — изгибающий момент; q — интенсивность распределённой нагрузки.

Объединяя (189) и (190), получим

. (191)

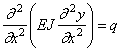
В задаче о свободных колебаниях нагрузкой для упругого скелета являются распределённые силы инерции:

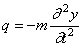
где m — интенсивность массы балки (масса единицы длины), и уравнение (191) принимает вид

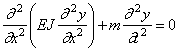
В частном случае постоянного поперечного сечения, когда EJ = const , m = const , имеем:

. (192)

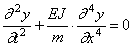
Для решения уравнения (192) полагаем, как и выше,

y = X ( x ) × T ( t ). (193)

Подставляя (193) в (192), приходим к уравнению:

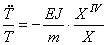
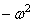
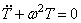
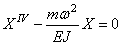
Для тождественного выполнения этого равенства необходимо, чтобы каждая из частей равенства была постоянной. Обозначая эту постоянную через , получим два уравнения:

; (194)

. (195)

Первое уравнение указывает на то, что движение носит колебательный характер с частотой .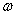

Второе уравнение определяет форму колебаний. Решение уравнения (195) содержит четыре постоянных и имеет вид

. (196)

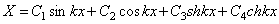
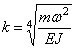
Удобно использовать вариант записи общего решения, предложенный А.Н.Крыловым:

, (197)

(198)

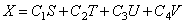
представляют собой функции А.Н.Крылова.

Обратим внимание на то, что S=1, T=U=V=0 при x=0. Функции S,T,U,V связаны между собой следующим образом:

(199)

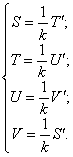
Поэтому производные выражения (197) записываются в виде

(200)

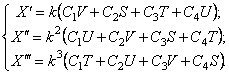
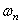
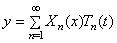
В задачах рассматриваемого класса число собственных частот бесконечно велико; каждой из них отвечает своя функция времени T_n и своя фундаментальная функция X_n . Общее решение получится путём наложения частных решений вида (193)

. (201)

Для определения собственных частот и формул необходимо рассмотреть граничные условия.

6.3.2. Граничные условия

Для каждого конца стержня можно указать два граничных условия .

Свободный конец стержня (рис. 70,а). Нулю равны поперечная сила Q=EJX»’T и изгибающий момент M=EJX»T. Поэтому граничные условия имеют вид

Шарнирно-опёртый конец стержня (рис.70,б). Нулю равны прогиб y=XT и изгибающий момент M=EJX»T. Следовательно, граничные условия таковы:

Защемленный конец (рис.70,в). Нулю равны прогиб y=XT и угол поворота 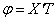. Граничные условия:

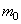
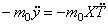
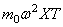
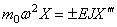
На конце стержня имеется точечный груз массы (рис.70,г). Его сила инерции может быть при помощи уравнения (194) записана так: ; она должна быть равна поперечной силе Q=EJX»’T , поэтому граничные условия принимают вид

; X»=0 . (205)

В первом условии знак плюс принимается в случае, когда точечный груз связан с левым концом стержня, и знак минус, когда он связан с правым концом стержня. Второе условие вытекает из отсутствия изгибающего момента .

Упруго-опертый конец стержня (рис.70,д). Здесь изгибающий момент равен нулю, а поперечная сила Q=EJX»’T равна реакции опоры 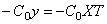(C_o-коэффициент жёсткости опоры).

X»=0 ; 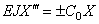(206)

(знак минус принимается в случае, когда упругая опора является левой, и знак плюс, когда она является правой).

6.3.3. Частотное уравнение и собственные формы

Развёрнутая запись граничных условий приводит к однородным уравнениям относительно постоянных C₁, C₂, C₃, C₄.

Чтобы эти постоянные не равнялись нулю, должен равняться нулю определитель, составленный из коэффициентов системы; это приводит к частотному уравнению. При этих операциях выясняются соотношения между C₁, C₂, C₃, C₄, т.е. определяются собственные формы колебаний (с точностью до постоянного множителя).

Проследим составление частотных уравнений на примерах.

Для балки с шарнирно-опёртыми концами согласно (203) имеем следующие граничные условия: X=0; X»=0 при x=0 и x= . При помощи (197)-(200) получим из первых двух условий: C₁=C₃=0. Два оставшихся условия можно записать в виде

Чтобы C₂ и C₄ не были равны нулю, необходимо равенство нулю определителя:

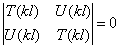
Таким образом, частотное уравнение имеет вид

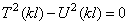
Подставляя выражения T и U, получим

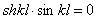
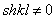
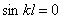
Так как , то окончательно частотное уравнение записывается так:

. (207)

Корни этого уравнения:

, ( n =1,2,3. ).

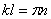
Учитывая (196), получим

. (208)

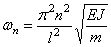
Перейдём к определению собственных форм. Из записанных выше однородных уравнений вытекает следующее соотношение между постоянными C₂ и C₄:

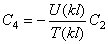
Следовательно, (197) приобретает вид

Согласно (207), имеем

, (209)

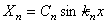
где 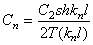— новая постоянная, значение которой остаётся неопределённым, пока не введены в рассмотрение начальные условия.

6.3.4. Определение движения по начальным условиям

Если требуется определить движение, следующее после начального возмущения, то необходимо указать для всех точек балки как начальные смещения, так и начальные скорости:

(210)

и использовать свойство ортогональности собственных форм:

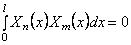
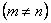
Общее решение (201) запишем так:

. (211)

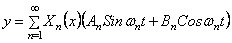
Скорость определяется выражением

. (212)

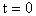
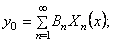
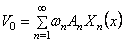
Подставляя в правые части уравнений (211) и (212) , а в левые части — предполагаемые известными начальные смещения и скорости, получим

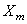
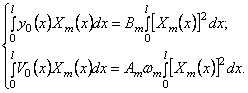
Умножая эти выражения на и интегрируя по всей длине, имеем

(213)

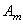
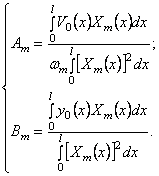
Бесконечные суммы в правых частях исчезли вследствие свойства ортогональности. Из (213) следуют формулы для постоянных и

(214)

Теперь эти результаты нужно подставить в решение (211).

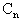
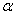
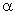
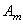
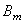
Снова подчеркнём, что выбор масштаба собственных форм несущественен. Если, например, в выражении собственной формы (209) принять вместо величину в раз большую, то (214) дадут результаты в раз меньшие; после подстановки в решение (211) эти различия компенсируют друг друга. Тем не менее часто пользуются нормированными собственными функциями, выбирая их масштаб таким, чтобы знаменатели выражений (214) равнялись единице, что упрощает выражения и .

6.3.5. Влияние постоянной продольной силы

Рассмотрим случай, когда колеблющаяся балка испытывает действие продольной силы N , величина которой не меняется в процессе колебаний. В этом случае уравнение статического изгиба усложняется и приобретает вид (при условии, что сжимающая сила считается положительной)

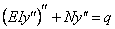
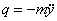
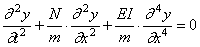
Полагая и считая жёсткость постоянной, получаем уравнение свободных колебаний

. (215)

Принимаем по-прежнему частное решение в виде .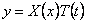

Тогда уравнение (215) распадается на два уравнения:

Первое уравнение выражает колебательный характер решения, второе определяет форму колебаний, а также позволяет найти частоты. Перепишем его таким образом:

(216)

где K определяется формулой (196), а

. (217)

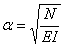
Решение уравнения (216) имеет вид

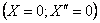
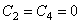
Рассмотрим случай, когда оба конца стержня имеют шарнирные опоры. Условия на левом конце дают . Удовлетворяя те же условия на правом конце, получим

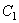
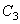
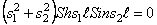
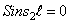
Приравнивая нулю определитель, составленный из коэффициентов при величинах и , приходим к уравнению

. (218)

Корни этого частотного уравнения:

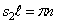
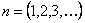
Следовательно, собственная частота определится из уравнения

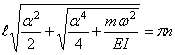
Отсюда при учёте (217) находим

. (219)

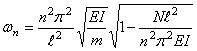
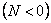
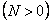
При растяжении частота увеличивается, при сжатии уменьшается. Когда сжимающая сила N приближается к критическому значению, корень стремится к нулю.

6.3.6. Влияние цепных усилий

Ранее продольная сила считалась заданной и не зависящей от перемещений системы. В некоторых практических задачах сопровождающая процесс поперечных колебаний продольная сила возникает вследствие изгиба балки и носит характер реакции опоры. Рассмотрим, например, балку на двух шарнирно-неподвижных опорах. При её изгибе возникают горизонтальные реакции опор, вызывающие растяжение балки; соответствующее горизонтальное усилие принято называть цепным усилием. Если балка совершает поперечные колебания, то цепное усилие будет изменяться во времени.

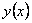
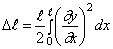
Если в мгновение t прогибы балки определяются функцией , то удлинение оси можно найти по формуле

Соответствующее цепное усилие найдём при помощи закона Гука

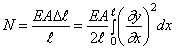
Подставим этот результат в (215) вместо продольной силы N (с учётом знака)

. (220)

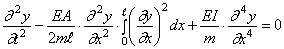
Полученное нелинейное интегродифференциальное уравнение упрощается при помощи подстановки

, (221)

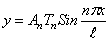
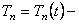
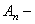
где безразмерная функция времени, максимальное значение которой можно положить равным любому числу, например, единице; амплитуда колебаний.

Подставляя (221) в (220), получим обыкновенное дифференциальное уравнение

, (222)

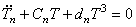
коэффициенты которого имеют следующие значения:

; .

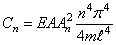
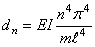
Дифференциальное уравнение (222) является нелинейным, следовательно, частота свободных колебаний зависит от их амплитуды.

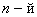
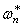
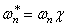
Точное решение для частоты поперечных колебаний имеет вид

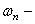
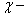
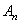
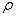
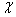
где частота поперечных колебаний, вычисленная без учёта цепных усилий; поправочный коэффициент, зависящий от отношения амплитуды колебаний к радиусу инерции поперечного сечения ; величина приводится в справочной литературе.

При соизмеримости амплитуды и радиуса инерции поперечного сечения поправка к частоте становится значительной. Если, например, амплитуда колебаний стержня круглого сечения равна его диаметру, то 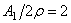, и частота почти в два раза больше, чем в случае свободного смещения опор.

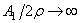
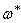
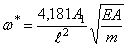
Случай соответствует нулевому значению радиуса инерции, когда изгибная жёсткость балки исчезающе мала — струна. При этом формула для даёт неопределённость. Раскрывая эту неопределённость, получим формулу для частоты колебаний струны

Эта формула относится к случаю, когда в положении равновесия натяжение равно нулю. Часто задачу о колебаниях струны ставят в других предположениях: считают, что перемещения малы, а растягивающая сила задана и остаётся неизменной в процессе колебаний.

При этом формула для частоты имеет вид

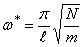
где N — постоянная растягивающая сила.

6.4. Влияние вязкого трения

Ранее предполагалось, что материал стержней идеально упругий и трение отсутствует. Рассмотрим влияние внутреннего трения, считая, что оно является вязким; тогда связь напряжений с деформациями описывается соотношениями

; . (223)

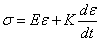
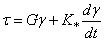
Пусть стержень с распределёнными параметрами совершает свободные продольные колебания. В этом случае продольная сила запишется в виде

. (224)

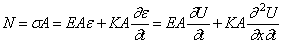
Из уравнения движения элемента стержня было получено соотношение (174)

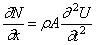
Подставляя сюда (224), приходим к основному дифференциальному уравнению

, (225)

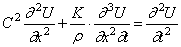
которое отличается от (175) вторым слагаемым, выражающим влияние сил вязкого трения.

Следуя методу Фурье, ищем решение уравнения (225) в виде

, (226)

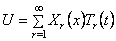
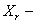
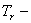
где функция только координаты x , а функция только времени t .

При этом каждый член ряда должен удовлетворять граничным условиям задачи, а вся сумма — также и начальным условиям. Подставляя (226) в (225) и требуя, чтобы равенство удовлетворялось для любого номера r , получим

, (227)

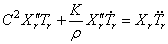
где штрихи обозначают дифференцирование по координате x , а точки — дифференцирование по времени t .

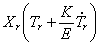
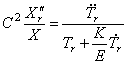
Разделив (227) на произведение , приходим к равенству

, (228)

левая часть, которого может зависеть только от координаты x , а правая — только от времени t . Для тождественного выполнения равенства (228) необходимо, чтобы обе части были равны одной и той же постоянной, которую обозначим через .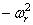

Из этого следуют уравнения

(229)

. (230)

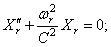
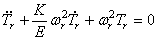
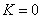
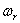
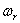
Уравнение (229) не зависит от коэффициента вязкости K и, в частности, остаётся таким же в случае идеально упругой системы, когда . Поэтому числа полностью совпадают с найденными ранее; однако, как будет показано ниже, величина даёт лишь приближённое значение собственной частоты. Отметим, что собственные формы совершенно не зависят от вязких свойств стержня, т.е. формы свободных затухающих колебаний совпадают с формами свободных незатухающих колебаний.

Теперь перейдём к уравнению (230), описывающему процесс затухающих колебаний; его решение имеет вид

, (231)

; (232)

. (233)

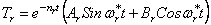
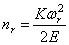
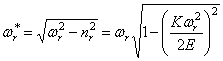
Выражение (232) определяет темп затухания, а (233) — частоту колебаний.

Таким образом, полное решение уравнения задачи

. (234)

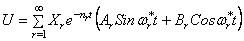
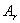
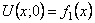
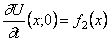
Постоянные и всегда можно найти по заданным начальным условиям. Пусть начальные смещения и начальные скорости всех сечений стержня заданы следующим образом:

; , (235)

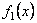
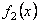
где и — известные функции.

Тогда при 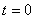, согласно (211) и (212), имеем

умножая обе части этих равенств на 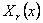и интегрируя в пределах всей длины стержня, получим

(236)

Соответственно условию ортогональности собственных форм все остальные слагаемые, входящие в правые части этих равенств, обращаются в нуль. Теперь из равенств (236) легко найти 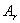и для любого номера r .

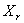
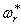
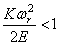
Рассматривая (232) и (234), заметим, что чем выше номер формы колебаний , тем быстрее её затухание. Кроме того, слагаемые, входящие в (234), описывают затухающие колебания, если есть действительное число. Из (233) видно, что это имеет место лишь для нескольких начальных значений r , пока выполняется неравенство

. (237)

При достаточно больших значениях r неравенство (237) нарушается и величина 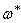становится мнимой. При этом соответствующие члены общего решения (234) уже не будут описывать затухающие колебания, но будут представлять апериодическое затухающее движение. Другими словами, колебания, в обычном смысле слова, выражает только некоторая конечная часть суммы (234).

Все эти качественные выводы относятся не только к случаю продольных колебаний, но и к случаям крутильных и изгибных колебаний.

6.5. Колебания стержней переменного сечения

В тех случаях, когда распределённая масса и сечение стержня переменны по его длине, следует вместо уравнения продольных колебаний (175) исходить из уравнения

. (238)

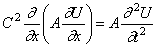
Уравнение крутильных колебаний (187) должно быть заменено уравнением

, (239)

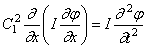
а уравнение поперечных колебаний (192) – уравнением

. (240)

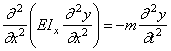
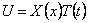
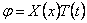
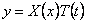
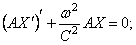
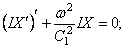
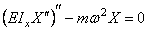
Уравнения (238)-(240) при помощи однотипных подстановок ; ; можно привести к обыкновенным дифференциальным уравнениям для функции

(241)

(242)

(243)

и одному однотипному уравнению для функции .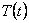

Уравнения (241)-(243) в отличие от уравнений, решённых выше, имеют переменные коэффициенты.

Замкнутую форму решений можно получить лишь в отдельных случаях, когда переменные 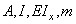определены специальными зависимостями. В общем случае неизбежен переход к приближённым методам. В частности, возможен путь, основанный на сосредоточении распределённой массы в ряде точек по длине стержня, после чего система сохраняет лишь конечное число степеней свободы, равное числу точек приведения. Используются также различные варианты вариационного метода и некоторые другие приближённые методы, о которых речь пойдёт ниже.

6.6. Колебания круговых колец

6.6.1. Колебания в плоскости кольца

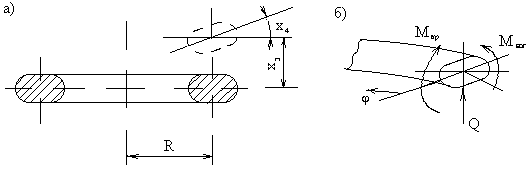
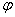
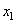
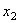
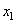
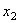
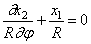
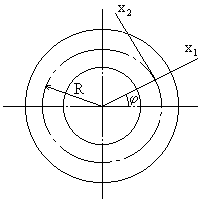
Рассмотрим круговой брус малой кривизны постоянного сечения с радиусом R осевой линии (рис.71,а). Будем считать груз нерастяжимым. Перемещение центра тяжести поперечного сечения, зафиксированного угловой координатой , можно разложить на радиальный и окружной компоненты — соответственно и . Из условия нерастяжимости оси бруса следует, что перемещения и связаны зависимостью:

. (244)

Угол поворота поперечного сечения бруса в процессе движения определяется формулой

. (245)

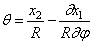
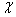
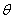
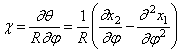
Изменение кривизны бруса равно производной от по дуге:

. (246)

Изгибающий момент в поперечном сечении кольца:

. (247)

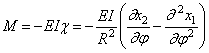
Теперь составим уравнение движения элемента 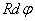бруса (рис.71,б).

Помимо перечисленных сил, на элемент действует также сила инерции:

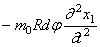
где 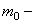масса единицы длины бруса.

Проектируя приложенные к элементу силы на радиус, получим

. (248)

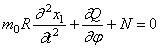
Равенство нулю суммы проекций всех сил на направление касательной приводит к уравнению:

. (249)

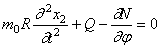
Уравнение моментов имеет вид

. (250)

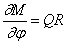
Исключим из (248) и (249) нормальную силу N , а поперечную силу Q заменим её значением из (250):

. (251)

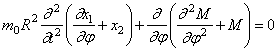
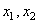
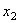
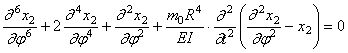
Подставляя сюда значение M из (247), получим уравнение движения в перемещениях , и, наконец, исключая один из компонентов перемещения, с помощью условия нерастяжимости (244) придём к уравнению, в которое входит единственная переменная :

. (252)

Решение уравнения движения (252) будем искать в виде

; .

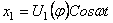
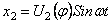
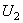
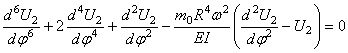
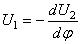
При этом для получается обыкновенное дифференциальное уравнение

, (253)

Согласно общим правилам решения дифференциальных уравнений, следует найти общее решение уравнения (253), включающее шесть постоянных, и подчинить его граничным условиям. На каждом конце бруса должны быть равны нулю либо компоненты перемещений 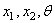, либо соответствующие им внутренние силы. Равенство нулю определителя системы, выражающей граничные условия, приводит к частотному уравнению.

Для замкнутого кольца граничные условия заменяются условиями периодичности, которые выполняются, если принять

; . (254)

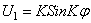
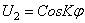
Подставляя (254) в (253), устанавливаем, что последнее удовлетворяется тождественно, если

. (255)

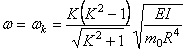
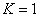
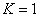
Формула (255) определяет частоты собственных колебаний кольца в своей плоскости. Значению соответствует нулевая частота, так как при формулы (254) описывают смещение кольца как жёсткого тела.

6.6.2. Колебания, перпендикулярные плоскости кольца

В этом случае положение поперечного сечения кольца в процессе движения характеризуется смещением 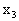его центра тяжести из плоскости кольца и углом поворота сечения х₄ (рис.72,а). В поперечном сечении кольца возникают изгибающие и крутящие моменты (рис.72,б), а также поперечная сила, перпендикулярная плоскости кольца.

Установим зависимость моментов от перемещений. Так как задача линейная, то рассмотрим сначала силовые факторы, связанные со смещением х₃, а затем — с х₄.

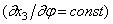
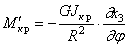
Если х₃ постоянно по длине окружности, то кольцо смещается как жёсткое целое, и внутренние силы не возникнут. Если х₃ изменяется в зависимости от центрального угла по линейному закону , то ось бруса превращается в винтовую линию, т.е. брус деформируется подобно витку пружины при растяжении. Известно, что в этом случае в поперечных сечениях возникает крутящий момент

где GJ _кр — крутильная жёсткость бруса.

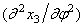
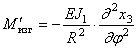
Если при этом отлична от нуля и вторая производная , то меняется кривизна бруса и возникает изгибающий момент

где J ₁ — момент инерции сечения относительно центральной оси, лежащей в плоскости кривизны.

Найдём силовые факторы, связанные с поворотом х₄. Если х₄ постоянно, то происходит осесимметричный изгиб кольца, причём в его сечениях возникает изгибающий момент

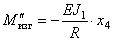
При переменном по длине повороте х₄ соседние сечения поворачиваются друг относительно друга и возникает крутящий момент

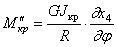
Суммируя силовые факторы, связанные с перемещениями х₃ и х_4, ,получаем

(256)

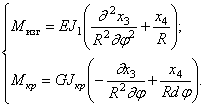
Составим уравнение движения элемента Rd 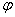бруса (рис.73).

Будем пренебрегать инерцией поворота элемента вокруг своей оси.

Условие динамического равновесия в направлении нормали к плоскости кольца приводит к уравнению:

. (257)

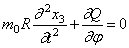
Сумма моментов относительно нормали к оси элемента:

. (258)

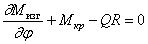
Сумма моментов относительно касательной к оси элемента:

. (259)

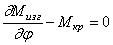
Исключая поперечную силу из (257) и (258) и заменяя моменты в полученном уравнении и уравнении (259) их значениями (256), приходим к системе уравнений, в которую входят только перемещения х₃ и х₄:

(260)

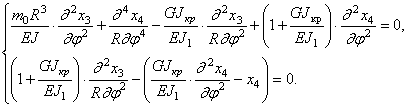
Ограничиваясь исследованием собственных колебаний замкнутого кольца, решение уравнений (260) можно представить в виде

x₃ = Acosk j × cos w t , x₄ = Bcosk j × cos w t . (261)

Подставляя значения (261) в уравнение движения (260), получим

(262)

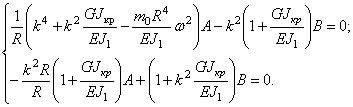
Из равенства нулю определителя этой системы получим частотное уравнение, корни которого — собственные частоты — таковы:

(263)

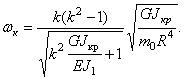
Наименьшая отличная от нуля частота соответствует k =2.

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

Колебания стержневых систем

Колебания стержневых систем

Собственные колебания стержневых систем с присоединенными массами

Если конструкция выведена из состояния равновесия, то она будет колебаться относительно равновесного состояния (положения статического равновесия). Частоты колебаний определяется физическими свойствами конструкции. Если к конструкции не приложены внешние динамические силы или силы сопротивления, то выведенная из равновесия конструкция будет колебаться бесконечно долго. Такие колебания называются собственными колебаниями конструкции. Амплитуды, частоты и формы собственных колебаний зависят от физических свойств конструкции и начального неравновесного состояния.

Рассмотрим пружину жесткостью r (рис.1,а) Жесткость пружины — сила, вызывающая удлинение пружины на единицу длины [r] — H/см, H/м. Если к пружине подвешен груз массой m, то в условиях статического равновесия пружина удлинится, и груз переместится на расстояние (рис. 1,б). Начало координат далее будем связывать с положением груза в условиях статического равновесия. Если груз находится и движется по горизонтальной плоскости, то х0=0.

Если масса выведена из равновесного состояния (рис. 1,в), то на него действуют силы упругости пружин — , вес пружины mg и сила инерции .

Учитывая равенство нулю сил статического равновесия, получаем дифференциальное уравнение движение массы m, подвешенной на пружине

, или . (1)

где — частота собственных колебаний (число колебаний в единицу времени)

Из характеристического уравнения получаем — мнимые корни и, следовательно,

(2)

Положив , , получим уравнение (2) в виде

, (3)

где А — амплитуда колебаний; параметр a определяет начальное положение и начальную скорость движения массы :

; (рис. 2).

Если заданы начальное положение и начальная скорость движения массы, то получим

, . (4)

Рассмотрим стержень длиной l с подвешенной на конце грузом с массой m (рис. 3) (считаем, что вес самого стержня мал по сравнению с грузом и влиянием собственного веса будем пренебрегать). По действием силы F удлинение стержня . При удлинении стержня на единицу длины необходимо приложить силу . Следовательно стержень можно рассматривать как пружину с жесткостью . Если стержень с подвешенной на конце массой вывести из равновесия, то частота колебаний массы будет определятся формулой . Как и в случае пружины форма колебаний определяется формулой (3), от положения массы при статическом равновесии, определяемой удлинении весом массы .

Рассмотрим однопролетную, шарнирно опертую балку с грузом в пролете балки (рис. 4). Прогиб в балке в точке приложения можно определить на основе интеграла Мор по формуле

, где — прогиб в точке приложения единичной . При колебании балки с массой m в i-й точке () получаем дифференциальное уравнение колебаний присоединенной массы

. (5)

Очевидно, дифференциальное уравнение колебаний массы, расположенной в пролете балки, соответствует уравнению колебаний массы с пружиной жесткостью . Следовательно, груз на балке колеблется в соответствие с формулой (3) с частотой

Эти выводы справедливы для любой балки, в том числе консольной, шарнирно опертой балки с консолями и для статически неопределимой балки, при расположении на балке 1-й массы.

Рассмотрим балку с несколькими присоединенными массами (рис. 5).

При действии на балку сосредоточенных поперечных сил прогиб в i-ой точке (с координатой хi) определяется по формуле

,. (6)

— прогиб в i-ой точке от действия единичной поперечной силы в j-ой точке.

Записывая уравнение (5) в точках присо6едененных масс от действия сосредоточенных сил в точках присоединенных масс, получим:

;

; (7)

Здесь точки показывают, что число масс может быть больше (меньше) трех. Число уравнений и число слагаемых в каждом уравнении соответствует числу присоединенных масс.

При колебаниях балки в точках присоединенных масс действуют инерционные силы

(8)

Тогда, система уравнений (6) приводится к системе дифференциальных уравнений колебаний балки с присоединенными массами:

;

; (9)

Здесь, как и в предыдущих примерах, перемещения уi отсчитываются от положения каждой массы при статическом равновесия балки.

Упругая система балки приводит к условию колебаний присоединенных масс с одинаковой частой (или комбинации частот), в соответствии с формулой (3)

. (10)

Подставляя решение (10) в систему дифференциальных уравнений (9) и сокращая на общий множитель , получаем систему однородных алгебраических уравнений:

;

; (11)

Однородная система имеет нулевое решение Аi = 0. Однако это означает отсутствие колебаний, что нас не удовлетворяет. Из теории алгебраических уравнений известно: чтобы однородная система алгебраических уравнений имела не нулевое решение, определитель системы уравнений должен бать равен нулю:

. (12)

Разделив определитель на w2, получаем эквивалентный определитель в виде

, . (13)

Значение определителя зависит от значений присоединенных масс, значений dij и параметра l. Однако неизвестным параметром является только параметр l, и его значение подбирается из условия равенства нулю определителя. Параметр l называется в математике собственным числом матрицы (матрицы определяемой коэффициентами определителя d без параметра l.[ ].

Раскрывая определитель можно получить полином относительно параметра l

, (14)

где k — количество присоединенных масс балки.

Отметим, что все собственные числа матрицы, определяющей собственные частоты колебаний, определяются действительными числами (если при расчете не были допущены ошибки). Это соответствует физической сущности задачи.

В математике известны аналитические методы определения корней полиномов не болей 4-й степени. Для полиномов более 4-ой степени точные методы вычисления корней существуют только для частных случаев. Для остальных полиномов корни вычисляются только приближенными численными методами. Поскольку задача нахождения собственных чисел матрицы является задачей, встречающейся во многих технических и физических процессах, то разработаны численные методы ее решения. Практически во всех алгоритмических языках имеются подпрограммы для вычисления собственных чисел матриц. Имеется такая подпрограмма и в комплексе «MathCad». Использование этой подпрограммы будет показано ниже.

После определения собственных чисел матрицы, вычисляются собственные частоты балки с присоединенными массами . Амплитуды колебаний и параметр a зависят от начального положения масс и начальных скоростей .

Рассмотрим раму с присоединенными массами (рис. 6).

При действии на раму сосредоточенных сил, справедлива формула (6) определения перемещения в i-той точке по заданному направлению. В отличие от балки, где присоединенная масса имеет одну степень свободы (поперечные прогибы балки), присоединенная масса рамы в плоскости может иметь две степени свободы ( горизонтальное и вертикальное перемещение), если перемещение не ограничено опорой.

Поэтому, прежде всего необходимо определить число степеней свободы присоединенных масс, связанные с изгибными деформациями рамы. Для этого, в заданной раме ставим дополнительные условные опоры, ограничивающие перемещения присоединенных масс, связанных с изгибными деформациями рамы (влиянием продольных деформаций стержней рамы пренебрегаем) (рис. 6,а). Дополнительные опоры на рис. 6,а. показаны пунктиром (условные опоры).

Вертикальное перемещение присоединенной массы m1 ограничено опорой А. Поэтому устанавливается только условная горизонтальная опора — 1. Вторая присоединенная масса имеет две степени свободы и требует установки вертикальной — 2 и горизонтальной — 3 условных опор. Условная опора 3 ограничивает горизонтальное перемещение всех присоединенных масс на горизонтальном стержне, и для них требуется установка только вертикальных условных опор условных опор: 4-я (присоединенная масса m4), 5-я (m6), 6-я (присоединенные массы m5 и m7). Для присоединенной массы m3 дополнительной условной опоры не требуется, так как ее вертикальное перемещение ограничено опорой А, о горизонтальное условной опорой — 3.

Отметим, что условная опора, ограничивающая перемещение присоединенных масс вдоль стержня, может быть установлена в любой точке этого стержня. Нумерация условных опор произвольна и может не совпадать с номером присоединенной массы, перемещение которой она ограничивает.

Для заданной рамы с 7-ю присоединенными массами (рис.6) установлено 6 условных опор, ограничивающих перемещения присоединенных масс. Следовательно, присоединенные массы (рама с присоединенными массами) имеют 6 степеней свободы.

Если присоединенные массы выведены из состояния статического равновесия, то происходит колебания системы с присоединенными массами. При колебании присоединенных масс, колебания происходят в направлении условных опор (перемещение уi). Все присоединенные массы, расположенные на одном стержне будут иметь одинаковое смещения (амплитуды колебаний, скорости и ускорения) вдоль стержня. Для учета инерционных сил введем понятие приведенных масс — масс колеблющихся в направлении i—ой условной опоры.

Для рамы с присоединенными массами (рис 6) имеем:

; ; ; ; ; .

Вывод уравнений колебаний рамы с присоединенными массами аналогичен выводу соответствующих уравнений балки с присоединенными массами. Число уравнений и слагаемых в них соответствует числу степеней свободы присоединенных масс и колебания происходят по направлению условных опор от действия приведенных масс. В результате получаем определитель.

. (15)

— перемещение по направлению i-ой условной опоры от единичной силы по направлению j-ой условной опоры (). Интегрирование производится по всем стержням рамы.

Рассмотрим пример определения частот колебаний рамы с присоединенными массами (рис. 7, а).

Условные дополнительные опоры и значения приведенных масс показаны на рис. 7,б. Присоединенные массы имеют 4 степени свободы. Для присоединенных масс получаем ; ; ; .

На рис. 7,б пронумерованы узловые точки, рама имеет 5 участков, на которых эпюры моментов от единичных сил в местах условных опор будут линейными.

Строим эпюры моментов в заданной раме от единичных сил в направлении условных опор. (рис. 8)

Пунктиром на участках показано отсутствие эпюры (изгибающие моменты на участке равны нулю).

Перемножая эпюры , , , по правилу Верещагина, получаем коэффициенты .

При перемножении эпюр учитываем длины и жесткости () участков, приведенные на рис. 7.

На стержнях с участками различной жесткости перемножение эпюр на каждом участке производится независимо. Если участки на стержне одинаковой жесткости эпюры могут перемножаться на каждом участке или на нескольких участках совместно для линейной эпюры на этих участках.

;

В скобках под формулами показаны номера участков, на которых перемножаются эпюры по правилу Верещагина

Учитывая, что все массы и коэффициенты dij имеют общие множители (m, a3/EJz) определи, умножаем на получая (определитель с безразмерными параметрами)

, (16)

где , (k1=4, k2=6, k1=1, k1=3); (, , , , , , , , , );

После вычисления собственных чисел матрицы , частоты колебаний системы с приведенными массами определяется по формуле .

Примечание. Собственные числа и частоты колебаний систем с присоединенными массами можно проводить без перехода к определителю с безразмерными параметрами, если все параметры (m, a3/EJz) на участках заданы.

Для определения частот колебаний рассматриваемой рамы используем программный комплекс «MathCad». Для вычисления собственных чисел матрицы в системе «MathCad».формируется матрица d коэффициентом матрицы без параметра l. Затем используется оператор . результат выводится на печать и используется для вычисления частот колебаний .

Фрагмент программы собственных частот колебаний рамы с присоединенными массами в системе «MathCad» (Коэффициенты dij вычисляются предварительно вручную):

Расчет частот собственных колебаний рамы с присоединенными массами

Коэффициенты dij

Матрица для вычисления собственных частот колебаний

Вычисление собственных чисел матрицы и собственных частот колебаний

Л и т е р а т у р а

1. Рекач устойчивости и динамики стержневых систем/ Конспект лекций для строителей. — М.: УДН, 1974. 108 с.

2. nОсновы динамики упругих систем. — М.: Изд-во РУДН, 1989. — 80 с.

3. Куприянов указания к расчету стержневых систем на динамическую нагрузку. — М.: Изд-во УДН, 1989. = 32 с.

Поперечные колебания стержней с сосредоточенными массами

Поперечных колебаний стержня С концентрированными массами При поперечных колебаниях штока очень часто вал должен быть заполнен техникой, особенно турбостроением, в котором используется прямая ось, несущая число дисков, так как такие валы имеют значительный размах, то очень важно определить скорость вращения этих валов критическую, а это самый важный фактор при

определении скорости вращения штока. Исследование поперечных колебаний вала начинается с рассмотрения упругой балки на двух опорах, несущих любое количество концентратов(точек) массы t1E t2, TP (рис. 538). Для решения задачи мы используем второй метод (см.§ 129), где нам нужно применить силу инерции-GP^;—mnwn>where^, согласно упругой системе без массы.. .. ^ —

Поперечное смещение (прогиб) оси T-T Bal-i * — вместо приложения массы■ > Ki t Людмила Фирмаль

движения ззв. Уравнения для этих перемещений обычно могут быть выражены в стандартной форме u i=a-pcache-t2^2612—… — &У2= — gp2vu2622 -…

mnwnb2n\ (20.74) шя= — mnwnbn. Движение в / направлении вызвано единичными силами, действующими в / направлении. Эти коэффициенты изгиба определяются методом Мора: Отчет где находится БТК 560Pk — = — м КВК=1. Где Me (x)и Mk(x) — изгибающие моменты, вызванные соответствующей

единичной силой Pi= = 1.: QiMck Е?— » Площадь участка-Mt (или часть MJ; продольная ось участка L4 расположена относительно центроида участка Q). Также напомним, что согласно теореме о взаимности перемещений(теорема Максвелла )), В4/г=БР£. Основная система уравнений(20.74) приводит к одному уравнению с одним

неизвестным в простейшем случае для колебательной системы С одной степенью свободы: это известное уравнение., Как -т^б^;^1^1621 — ^Г^Д- Один. C=7 грамм- — То Для системы с двумя степенями свободы на основе уравнения (20.74) получены две системы уравнений с двумя неизвестными функциями отклонения wL и Y2: при решении системы уравнений w2=(20.74) функция отклонения может быть wt=sin (Yu/4-a). Подставляя это уравнение в основное уравнение (20.74), получаем следующую однородную систему алгебраических уравнений для неизвестных амплитуд

и частот.: Xj (pcbcco2— 1)4- 4- • • • 4- HY / plb1ya НС (3)2.. . m, Finn n (s>2-1N apisav, показывая в развернутом виде этот определитель, коэффициент под разными углами ■ • •» ( Ю 2>. > ( =АТЛ грех( Людмила Фирмаль

найти частотное уравнение ® 4 (bi^gg612) t1t2—(s>2 (bcgp^f- 622^2) 4

— 0, здесь первая и вторая частоты колебаний определяются соответствующими уравнениями *- /**«fcj-з[6У+е» — ст+ * > * * ¶Пример 85. Определите собственную частоту луча (рис. 539), несущие три одинаковых сосредоточенных груза массой т каждый. Сначала определим движение точек приложения изделия под действием единичных сил P g=1, P2==1 и P3-1. Для этого построим диаграмму изгибающего момента от заданной единицы силы (рис. 540). Использование коэффициентов ( Один. Дж Один. Я Два. Два. Л-В Е З И г^г ТП thtp.. — lS, 3 5<_L 6/6 Малрой Верещагин, найдите

смещение от одного рычага: 6тс= = 75А?;В22=243L?;621=612—^23-P7L;613=631=51/g, где Л== £ 9 * 1296PJ’ Создайте определитель, аналогичный формуле (6/L>20.76) со значением: 75m W-I1I7mk& * Sim ka2 U7mka2 2& > mka2-1 117mto2 51М ТО2 117WI & 02 75mk (^- 1 Запишите определитель результата в расширенном виде, найдите формулу 77 760 (M W) для частоты 3-12 096 (m W) 2+393m W-1=0. Это уравнение имеет следующие три корня, соответствующие трем значениям собственной окружной частоты рассматриваемой вибрации упругой системы. (20.80)) (20.81)) 36,00 1/ — Эдж Я Г М Л’(20.82)

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

источники:

http://pandia.ru/text/80/149/18791.php

http://lfirmal.com/poperechnye-kolebaniya-sterzhnej-s-sosredotochennymi-massami/