Уравнение колебаний в комплексном виде

Колебательное движение

Определение и основные понятия колебательного движения

Колебательное движение (колебание) — это любое движение или изменение состояния, которое повторяется во времени, соответственно повторяются значения физических величин, которые характеризуют данное движение или состояние.

Различные физические явления представляют собой колебания: звуковые колебания, электромагнитные, механические и т.д. У всех этих явлений существует общее в законах и математических методах, при помощи которых они описываются.

Колебательное движение называется периодическим, если переменные параметры этих колебаний повторяются через равные промежутки времени.

Колебания называются свободными, если они происходят в системе, на которую не действуют внешние силы (или действие их взаимно скомпенсировано).

Такая система один раз выводится из состояния равновесия. Если колебательная система консервативная, то рассеяния энергии при колебаниях нет. В таком случае свободные колебания являются незатухающими. Свободные незатухающие колебания, которые происходят под воздействием упругих сил, являются гармоническими.

Периодом незатухающих колебаний называют минимальный промежуток времени ($T$) по истечении которого происходит повторение значений всех физических параметров, которые характеризуют колебание.

Частотой колебаний ($\nu $) называют величину обратную периоду колебаний, это количество полных колебаний, которое совершает колебательная система:

Гармонические колебания

Самым простым типом колебаний считают гармонические колебания.

Колебания называют гармоническими, если изменения физической величины описывается при помощи закона синуса или косинуса.

Пусть происходят гармонические колебания никоторого параметра $s$, тогда они описываются как:

где $A=s_$ — амплитуда колебаний (постоянна во времени); $<\omega >_0$ — циклическая (круговая) частота колебаний (с течением времени не изменяется); $\varphi $ — начальная фаза колебаний (фаза при $t=0$); $(<\omega >_0t+\varphi )$ — фаза колебаний. Величина $s$ изменяется $-A\le s\le $+A.

Те же самые колебания можно описать как:

За время равное периоду колебаний фаза изменяется на величину равную $2\pi $, поэтому:

Циклическая частота $<\omega >_0$ равна числу полных колебаний, которые совершаются колебательной системой за $2\pi $c:

Дифференциальное уравнение колебательного движения

Линейное дифференциальное уравнение гармонических колебаний представляет собой выражение:

Решениями уравнения (6) является выражения (2) и (3). Уравнение вида (6) называют уравнением гармонического осциллятора, а колебательную систему, которая совершает эти колебания гармоническим осциллятором (примерами гармонических осцилляторов являются: пружинный маятник, физический маятник, электрический колебательный контур).

Представление гармонических колебаний в комплексной форме

Сложение, разложение на составляющие и другие операции при изучении гармонических колебаний проще проводить, если представить уравнение гармонических колебаний в комплексной форме. При этом вместо действительной формы записи (2 и 3) используют комплексную:

Величина $\tilde$ является комплексной и не дает реального физического отклонения, которое характеризуется вещественной величиной $s$ (2,3). Но мнимую часть величины $\tilde$ можно рассматривать как действительной гармоническое колебание выраженное синусом. С другой стороны действительная часть (7) равная:

представляет собой вещественное гармоническое колебание. Поэтому гармонические колебания можно записывать в комплексном виде (7) и выполнять все требуемые расчёты. При получении результата нужно взять действительную или мнимую часть для перехода к физическим величинам.

Примеры задач на колебательное движение

Задание: Материальная точка, массой $m=<10>^<-4>$кг совершает колебания согласно закону: $x=0,05<\cos (20t)\ >$. Каково максимальное значение возвращающей силы, действующей на точку ($F_$)?

Решение:В соответствии со вторым законом Ньютона на материальную точку действует сила:

Так как колебания точки происходят по оси X, то получим:

Вычислим вторую производную от $x\left(t\right)=0,05$, имеем:

Подставим правую часть выражения (1.3) в (1.2) вместо соответствующей производной, учитывая массу точки получаем:

Максимальное значение косинуса равно единице, значит:

Ответ: $\left|F_\right|=2\cdot <10>^<-3>$Н

Задание: Нарисуйте траекторию колебательного движения точки, если она участвует одновременно в двух взаимно перпендикулярных колебаниях, которые описывают законы:

Решение:Определим, каким является уравнение колебательного движения точки в плоскости XY. Используем формулу косинуса двойного угла:

Из условия задачи:

Получаем, что $y$ равен:

Ответ: $y\left(x\right)=A-\frac<<2x>^2>$

Механические гармонические колебания

Вы будете перенаправлены на Автор24

Большое число физических процессов можно представить как малое отклонение от положения равновесия.

Рассмотрим систему, которая состоит из шарика, укрепленного на упругой пластине (рис.1). В положении равновесия пластина немного изогнута, при этом шарик находится в покое в некоторой точке $A$. Отклоним этот шарик вертикально и отпустим. Вопрос: как будет происходить перемещение данного шарика?

Рисунок 1. Колебательная система. Автор24 — интернет-биржа студенческих работ

Сила ($F(x)$), которая действует на шарик (рис.1) является сложной функцией параметра ($x$), характеризующего отклонение от равновесного положения в направлении вертикали. При этом решение дифференциального уравнения вида:

будет весьма сложным. Даже если его можно будет решить, то будут сложности с его анализом.

Уравнение гармонических колебаний

В большом числе случаев на практике представляет интерес поведение системы, совершающей колебания не при всех возможных отклонениях, а только при очень небольших отклонениях.

В этом случае решение уравнения движения (1) существенно упрощается. Какой бы сложной не была функция силы, ее можно разложить в ряд Тейлора. При этом в реальных задачах физики отличным от нуля бывает $xF’(0)$, уравнение движения при очень небольших отклонениях от равновесия принимает вид:

где введено обозначение: $F’(0)=-k>0$.

Уравнение вида (2) получается при исследовании многих явлений физики. В рассмотренном выше примере параметр $x$ — это расстояние от положения равновесия. Но $x$ можно понимать как заряд конденсатора, в колебательном контуре что-то иное.

Уравнение вида (2) называют уравнением гармонических колебаний, при этом систему, совершающую данные малые колебания, считают линейным (гармоническим) осциллятором.

Готовые работы на аналогичную тему

Часто рассматриваемыми примерами гармонических осцилляторов в механике являются:

• тело на упругой пружине (пружинный маятник);
• тело на нерастяжимом и невесомом подвесе (нити) (математический маятник);
• физический маятник.

Уравнение гармонических колебаний обычно представляют в виде:

Гармонические функции

Прямой подстановкой несложно убедиться в том, что решением уравнения гармонических колебаний (3) являются тригонометрические функции (и их комбинации):

Поскольку дифференциальное уравнение (3) является линейным, то сумма решений этого уравнения и произведение их на постоянную величину, так же является решением этого же уравнения.

Следовательно, можно записать, что общее решение уравнения (3) представляется в виде:

$x(t)=C_1\sin (\omega t)+C_2 \cos (\omega t)(4),$

где $C_1$ и $C_2$ — постоянные коэффициенты. Функцию вида (4) называют гармонической.

Параметры, характеризующие гармонические колебания.

Равенство (4) часто записывают в ином виде:

И так, уравнение гармонических колебаний запишем в виде:

$x(t)=C \sin (\omega t+\varphi)$ или $x(t)=C \cos (\omega t+\varphi_1)$.

При этом параметр $C$ является амплитудой колебаний; $\omega$ — циклическая (круговая частота колебаний); $\omega t+\varphi $ — фаза колебаний; величина фазы колебаний (\varphi) в момент времени, принятый за начальный называется начальной фазой (часто просто фазой).

Из вида уравнений колебаний (5) можно сделать вывод о том, что параметр $x$ приобретает одинаковые значения спустя время, равное:

Функции (5) называют периодическими. Физическая величина $T$ называется периодом колебаний.

Гармонические колебания являются периодическими. Обратное не всегда справедливо. Не каждая периодическая функция является гармонической. Функция считается гармонической только в том случае, если ее можно представить в виде (5), и она имеет определенные:

Комплексная запись гармонических колебаний

Исследуя гармонические колебания, необходимо производить разные математические операции с описывающими их уравнениями. Эти процедуры существенно упрощаются, если применять теорию комплексных чисел и представлять гармонические колебания в комплексной форме.

В системе координат Декарта действительная часть комплексного числа откладывается по оси абсцисс, мнимая – по оси ординат. Далее используют формулу Эйлера:

Форма записи гармонического колебания в виде тригонометрических функций (5) называется действительной. Комплексная их запись:

Параметр $\tilde$ — это комплексное число и не может дать реального физического отклонения, которое определяется вещественной величиной $x$ вида (5). Но мнимая компонента $\tilde$ может быть рассмотрена как действительное гармоническое колебание (5), которое определено синусом. При этом действительная часть $\tilde$ равна $C \cos (\omega t +\varphi)$, она представляет вещественное гармоническое колебание.

Используя комплексную запись гармонических колебаний, после выполнения всех математических операций, в полученном результате для того, чтобы перейти к реальным физическим параметрам берут действительную или мнимую часть выражения, которое получили.

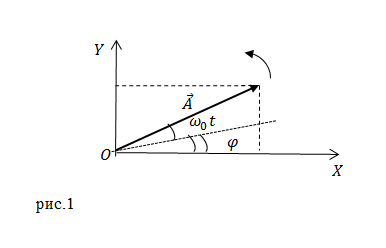
График гармонического колебания, которое представлено в комплексном виде, показан на рис.2. При колебаниях комплексный вектор $\vec C$ совершает вращательные движения около начала координат против часовой стрелки. Скорость вращения его составляет:

где $T$ — период колебаний. Проекции $\vec C$ на оси – это действительные физические колебания.

Рисунок 2. График гармонического колебания. Автор24 — интернет-биржа студенческих работ

Гармонические колебания

О чем эта статья:

9 класс, 11 класс, ЕГЭ/ОГЭ

Механические колебания

Механические колебания — это физические процессы, которые точно или приблизительно повторяются через одинаковые интервалы времени.

Колебания делятся на два вида: свободные и вынужденные.

Свободные колебания

Это колебания, которые происходят под действием внутренних сил в колебательной системе.

Они всегда затухающие, потому что весь запас энергии, сообщенный в начале, в конце уходит на совершение работы по преодолению сил трения и сопротивления среды (в этом случае механическая энергия переходит во внутреннюю). Из-за этого свободные колебания почти не имеют практического применения.

Вынужденные колебания

А вот вынужденные колебания восполняют запас энергии внешним воздействием. Если это происходит каждый период, то колебания вообще затухать не будут.

Вынужденные колебания — это колебания, которые происходят под действием внешней периодически меняющейся силы.

Частота, с которой эта сила воздействует, равна частоте, с которой система будет колебаться.

Например, качели. Если вас кто-то будет на них качать, каждый раз давая толчок, когда вы приходите в одну и ту же точку — такое колебание будет считаться вынужденным.

Это колебание все еще будет считаться вынужденным, если вас будут раскачивать из положения равновесия. Просто в данном случае амплитуда (о которой речь пойдет чуть ниже) будет увеличиваться с каждым колебанием.

Автоколебания

Иногда вынужденному колебанию не нужно внешнего воздействия, чтобы случиться. Бывают такие системы, в которых это внешние воздействие возникает само из-за способности регулировать поступление энергии от постоянного источника.

У автоколебательной системы есть три важных составляющих:

• сама колебательная система
• источник энергии
• устройство обратной связи, обеспечивающей связь между источником и системой

Часы с кукушкой — пример автоколебательной системы. Гиря на ниточке (цепочке) стремится вращать зубчатое колесо (храповик). При колебаниях маятника анкер цепляет за зубец, и вращение приостанавливается.

Но в результате маятник получает толчок, компенсирующий потери энергии из-за трения. Потенциальная энергия гири, которая постепенно опускается, расходуется на поддержание незатухающих колебаний.

Характеристики колебаний

Чтобы перейти к гармоническим колебаниям, нам нужно описать величины, которые помогут нам эти колебания охарактеризовать. Любое колебательное движение можно описать величинами: период, частота, амплитуда, фаза колебаний.

Период — это время одного полного колебания. Измеряется в секундах и обозначается буквой T.

Формула периода колебаний

T = t/N

N — количество колебаний [—]

Также есть величина, обратная периоду — частота. Она показывает, сколько колебаний совершает система в единицу времени.

Формула частоты

ν = N/t = 1/T

N — количество колебаний [—]

Амплитуда — это максимальное отклонение от положения равновесия. Измеряется в метрах и обозначается либо буквой A, либо x max .

Она используется в уравнении гармонических колебаний:

Гармонические колебания

Простейший вид колебательного процесса — простые гармонические колебания, которые описывают уравнением:

Уравнение гармонических колебаний

x — координата в момент времени t [м]

t — момент времени [с]

(2πνt) в этом уравнении — это фаза. Ее обозначают греческой буквой φ

Фаза колебаний

t — момент времени [с]

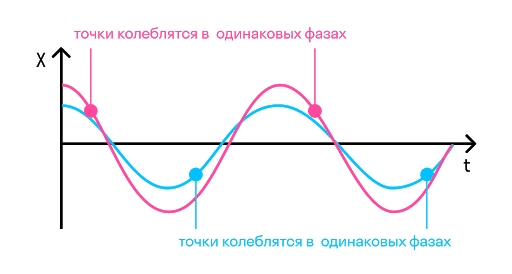
Фаза колебаний — это физическая величина, которая показывает отклонение точки от положения равновесия. Посмотрите на рисунок, на нем изображены одинаковые фазы:

Например, в тех же самых часах с кукушкой маятник совершает колебания. Он качается слева направо и приходит в самую правую точку. В той же фазе он будет находиться, когда придет в ту же точку, идя справа налево. Если мы возьмем точку на сантиметр левее самой правой, то идя в нее не слева направо, а справа налево, мы получим уже другую фазу.

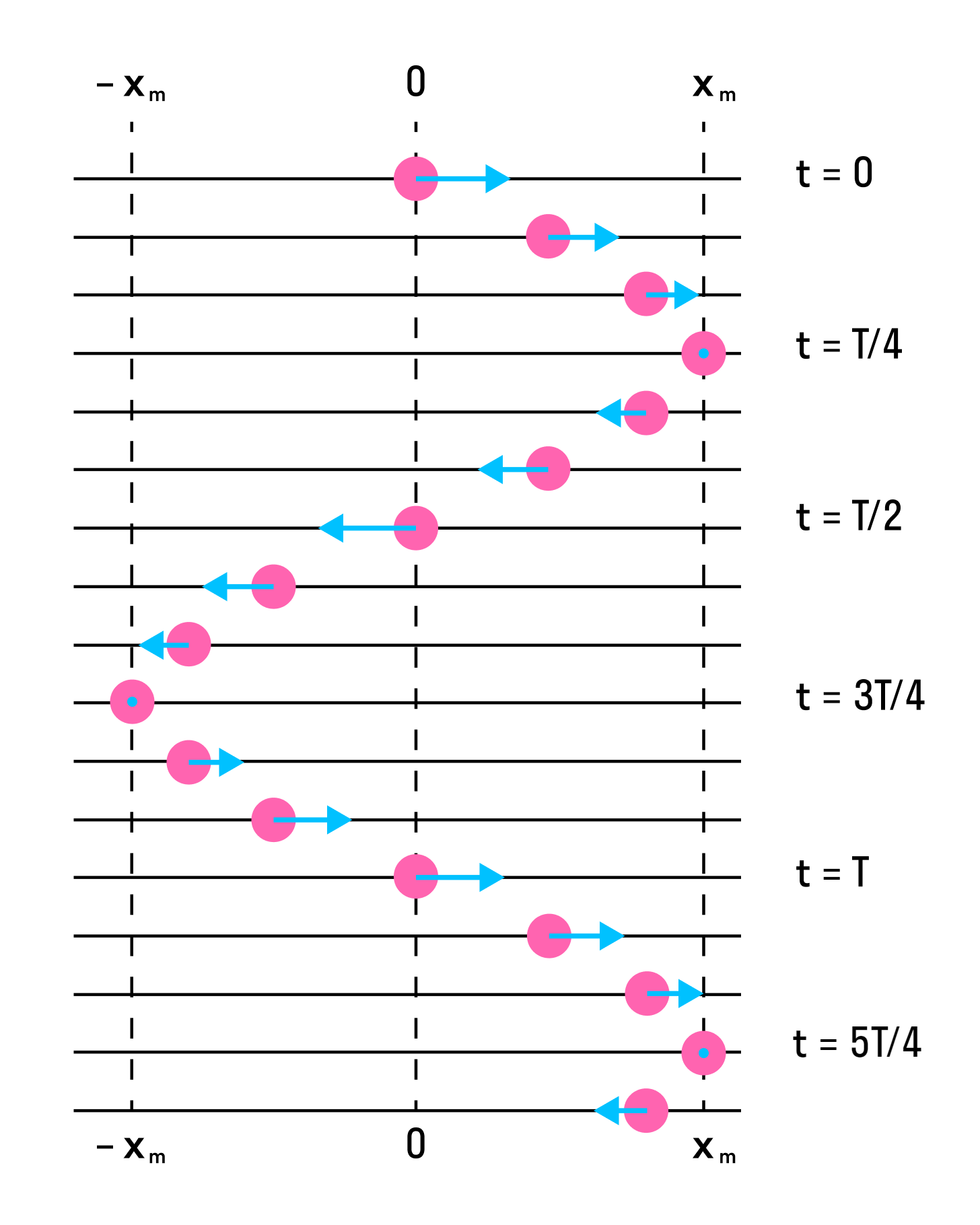
На рисунке ниже показаны положения тела через одинаковые промежутки времени при гармонических колебаниях. Такую картину можно получить при освещении колеблющегося тела короткими периодическими вспышками света (стробоскопическое освещение). Стрелки изображают векторы скорости тела в различные моменты времени.

Если изменить период, начальную фазу или амплитуду колебания, графики тоже изменятся.

На рисунке ниже во всех трех случаях для синих кривых начальная фаза равна нулю, а в последнем (с) — красная кривая имеет меньшую начальную фазу.

В первом случае (а) красная кривая описывает колебание, у которого амплитуда больше колебания, описанного синей линией.

Во втором случае (b) красная кривая отличается от синей только значением периода — у красной период в два раза меньше.

Математический маятник

Математический маятник — отличный пример гармонических колебаний. Если мы подвесим шарик на нити, то это еще не будет математическим маятником — пока он только физический.

Математическим этот маятник станет, если размеры шарика много меньше длины нити (тогда этими размерами можно пренебречь и рассматривать шарик как материальную точку), растяжение нити очень мало, а масса нити во много раз меньше массы шарика.

Математическим маятником называется система, которая состоит из материальной точки массой m и невесомой нерастяжимой нити длиной l, на которой материальная точка подвешена, и которая находится в поле силы тяжести (или других сил).

Период малых колебаний математического маятника в поле силы тяжести Земли определяется по формуле:

Формула периода колебания математического маятника

l — длина нити [м]

g — ускорение свободного падения [м/с 2 ]

На планете Земля g = 9,8 м/с 2

Пружинный маятник

Пружинный маятник — это груз, прикрепленный к пружине, массой которой можно пренебречь.

В пружинном маятнике колебания совершаются под действием силы упругости.
Пока пружина не деформирована, сила упругости на тело не действует.

Формула периода колебания пружинного маятника

m — масса маятника [кг]

k — жесткость пружины [Н/м]

Закон сохранения энергии для гармонических колебаний

Физика — такая клевая наука, в которой ничего не исчезает бесследно и не появляется из ниоткуда. Эту особенность описывает закон сохранения энергии.

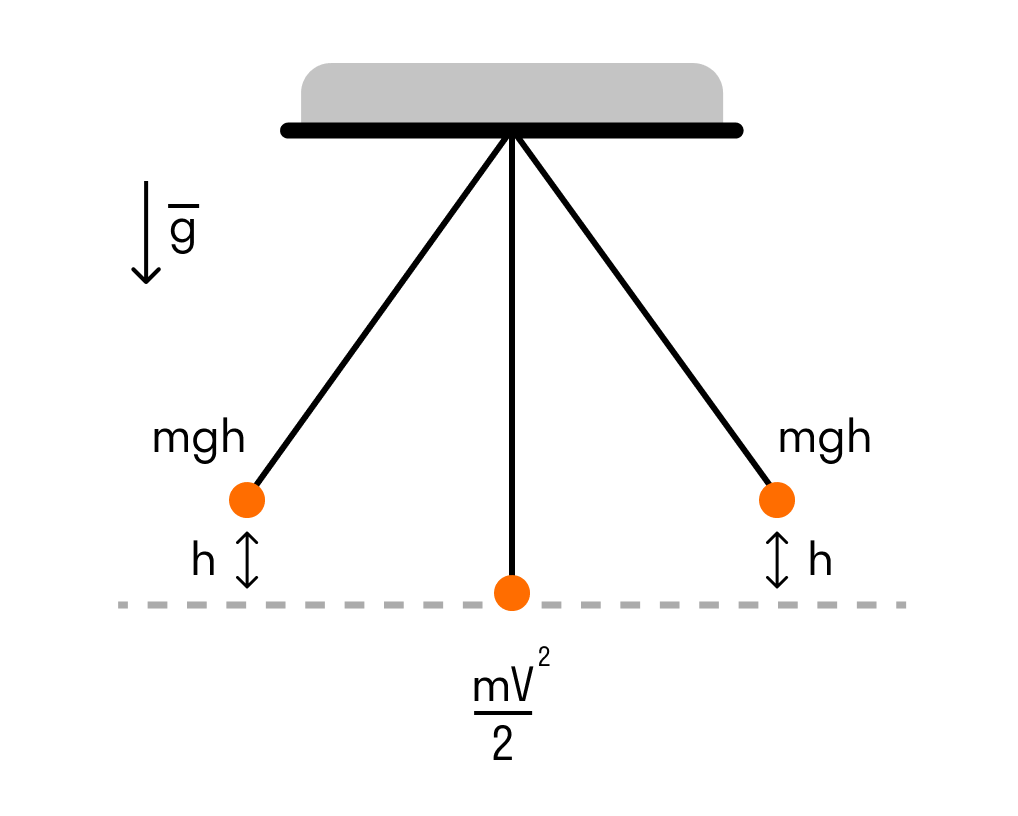
Рассмотрим его на примере математического маятника.

• Когда маятник отклоняют на высоту h, его потенциальная энергия максимальна.
• Когда маятник опускается, потенциальная энергия переходит в кинетическую. Причем в нижней точке, где потенциальная энергия равна нулю, кинетическая энергия максимальна и равна потенциальной энергии в верхней точке. Скорость груза в этой точке максимальна.

Онлайн-курсы физики в Skysmart не менее увлекательны, чем наши статьи!