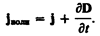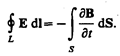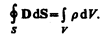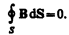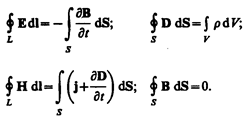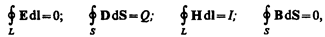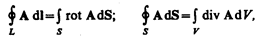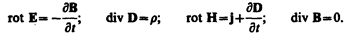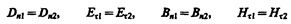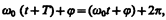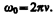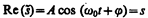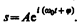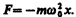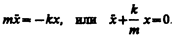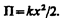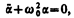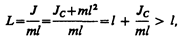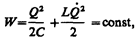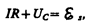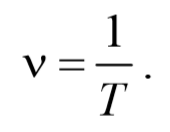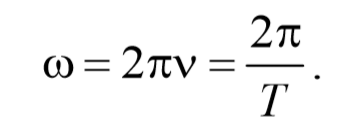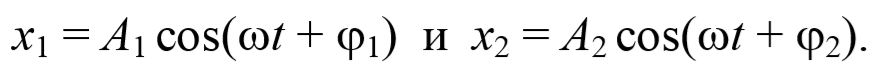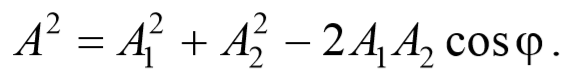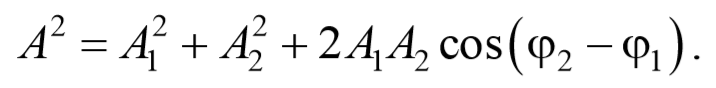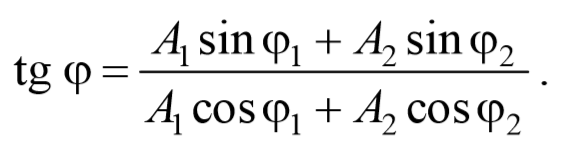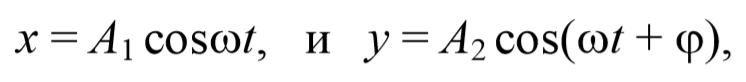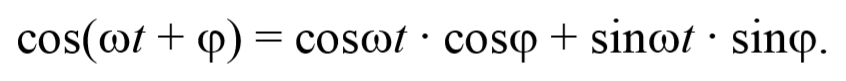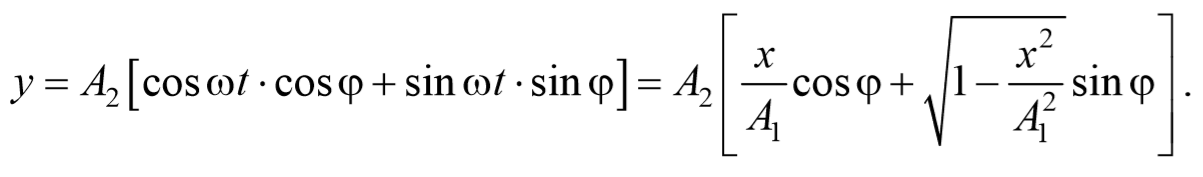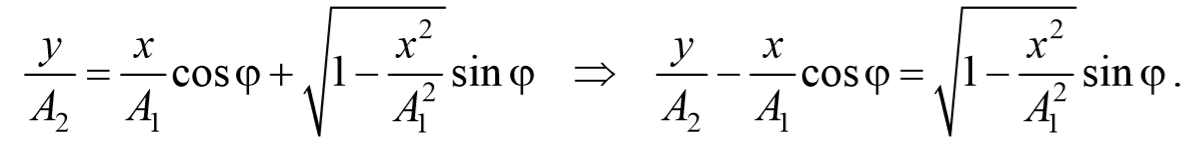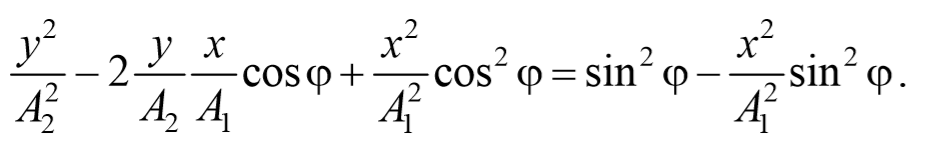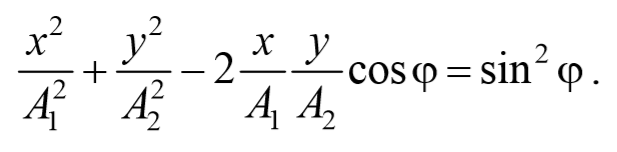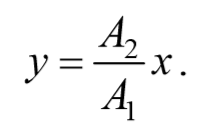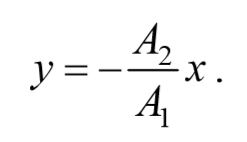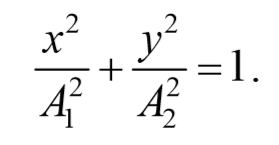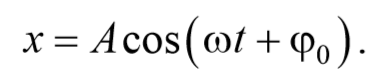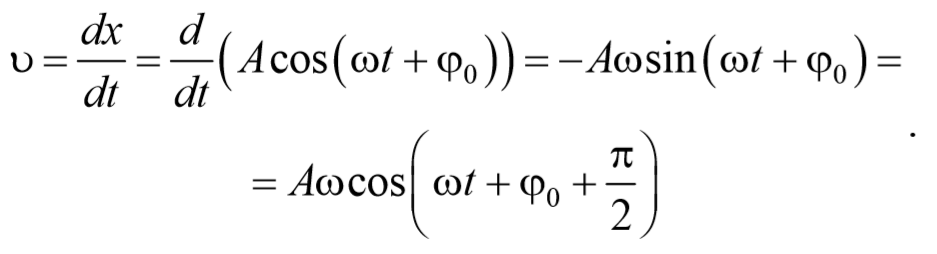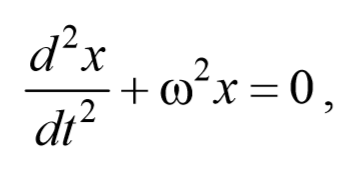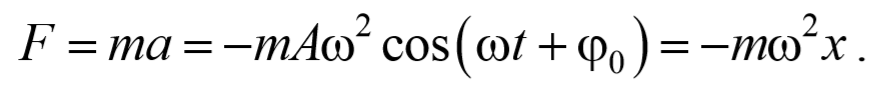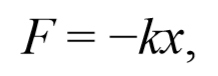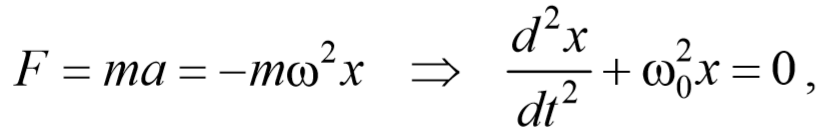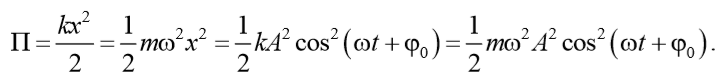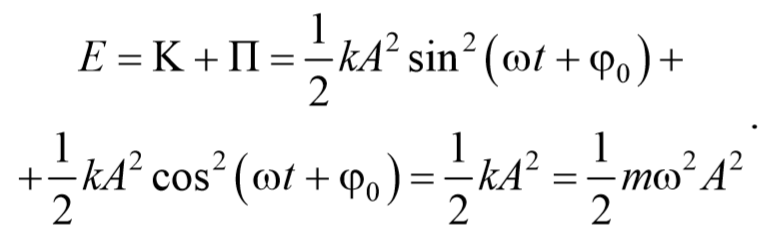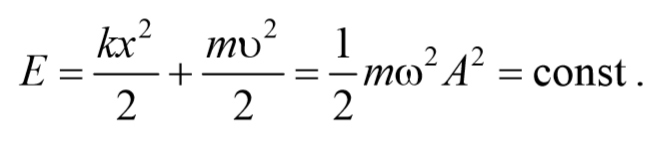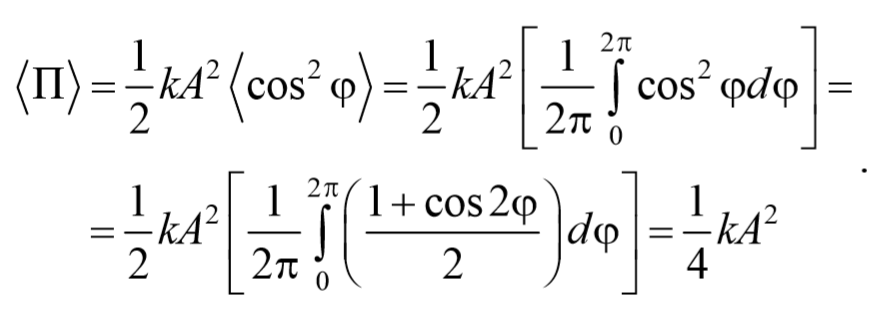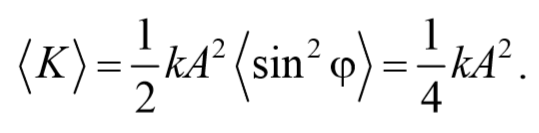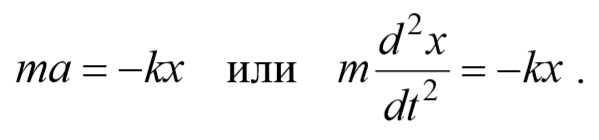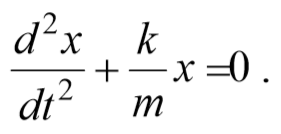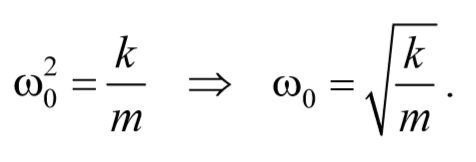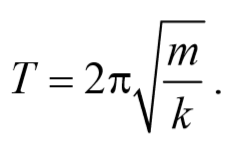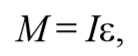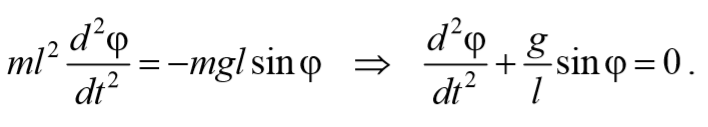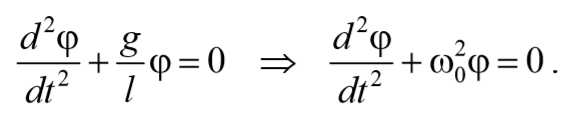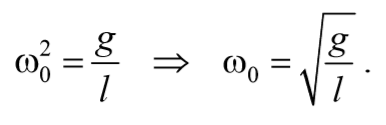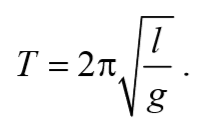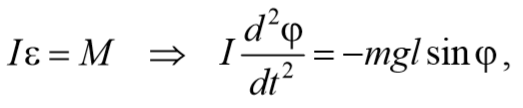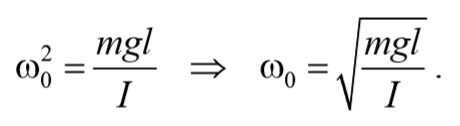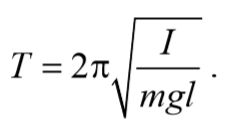А.Н. Тихонов, А.А. Самарский
Уравнения математической физики
Глава I. Классификация дифференциальных уравнений с частными производными
1. Дифференциальные уравнения с двумя независимыми переменными. 2. Классификация уравнений 2-го порядка со многими независимыми переменными. 3. Канонические формы линейных уравнений с постоянными коэффициентами. Задачи к главе I
Глава II. Уравнения гиперболического типа
1. Уравнение малых поперечных колебаний струны. Уравнение продольных колебаний стержней и струн. 3. Энергия колебания струны. 4. Вывод уравнения электрических колебаний в проводах. 5. Поперечные колебания мембраны. 6. Уравнения гидродинамики и акустики. 7. Граничные и начальные условия. 8. Редукция общей задачи. 9. Постановка краевых задач для случая многих переменных. 10. Теорема единственности. Задачи.
1. Формула Даламбера. 2. Физическая интерпретация. 3. Примеры. 4. Неоднородное уравнение. Устойчивость решении. 6. Полуограниченная прямая и метод продолжений. 7. Задачи для ограниченного отрезка. 8. Дисперсия волн. 9. Интегральное уравнение колебаний. 10. Распространение разрывов вдоль характеристик. Задачи.
1. Уравнение свободных колебаний струны. 2. Интерпретация решения. 3. Представление произвольных колебаний в виде суперпозиции стоячих воли. 4. Неоднородные уравнения. 5. Общая первая краевая задача. 6. Краевые задачи со стационарными неоднородностями. 7. Задачи без начальных условий. 8. Сосредоточенная Сила. 9. Общая схема метода разделения переменных. Задачи.
1. Постановка задачи. 2. Метод последовательных приближений дли задачи Гурса. Задачи.
1. Сопряженные дифференциальные операторы. 2. Интегральная форма решения. 3. Физическая интерпретации функции Римана. 4. Уравнения с постоянными коэффициентами. Задачи к главе II
Приложения к главе II
1. Постановка задачи. 2. Собственные колебания нагруженной струны. 3. Струна с грузом на конце. 4. Поправки для собственных значений.
1. Уравнения газодинамики. Закон сохранения энергии. 2. Ударные волны. Условия динамической совместности. 3. Слабые разрывы.
1. Уравнения, описывающие процесс сорбции газа. 2. Асимптотическое решение.
Глава III. Уравнения параболического типа
1. Линейная задача о распространении тепла. 2. Уравнение диффузии. 3. Распространение тепла в пространстве. 4. Постановка краевых задач. 5. Принцип максимального значения. 6. Теорема единственности. 7. Теорема единственности для бесконечной прямой.
1. Однородная краевая задача. 2. Функция источника. 3. Краевые задачи с разрывными начальными условиями. 4. Неоднородное уравнение теплопроводности. 5. Общая первая краевая задача. Задачи.
1. Распространение тепла на бесконечной прямой. Функция источника для неограниченной области. 2. Краевые задачи для полуограниченной прямой.
Задачи к главе III
Приложения к главе III
1. Функция источника для бесконечной прямой. 2. Краевые задачи для квазилинейного уравнения теплопроводности.
1. Определение d -функции. 2. Разложение d -фикции в ряд Фурье. 3. Применение d -функции к построению функции источника.
Глава IV. Уравнения эллиптического типа
1. Стационарное тепловое поле. Постановка краевых задач. 2. Потенциальное течение жидкости. Потенциал стационарного тока и электростатического поля. 3. Уравнение Лапласа в криволинейной системе координат. 4. Некоторые частные решения уравнения Лапласа. 5. Гармонические функции и аналитические функции комплексного переменного. 6. Преобразование обратных радиусов-векторов.
1. Формулы Грина. Интегральное представление решения. 2. Некоторые основные свойства гармонических функций. 3. Единственность и устойчивость первой краевой задачи. 4. Задачи с разрывными граничными условиями. 5. Изолированные особые точки. 6. Регулярность гармонической функции трех переменных в бесконечности. 7. Внешние краевые задачи. Единственность решения для двух- и трехмерных задач. 8. Вторая краевая задача. Теорема единственности.
1. Первая краевая задача для круга. 2. Интеграл Пуассона. 3. Случай разрывных граничных значений.
1. Функция источника для уравнения D u=0 и ее основные свойства. 2. Метод электростатических изображений и функция источника для сферы. 3. Функция источника для круга. 4. Функция источника для полупространства.
1. Объемный потенциал. 2. Плоская задача. Логарифмический потенциал. Несобственные интегралы. 4. Первые производные объемного потенциала. 5. Вторые производные объемного потенциала. 6. Поверхностные потенциалы. 7. Поверхности и кривые Ляпунова. 8. Разрыв потенциала двойного слоя. 9. Свойства потенциала простого слоя. 10. Применение поверхностных потенциалов к решению краевых задач. 11. Интегральные уравнения, соответствующие краевым задачам. Задачи к главе IV
Приложения к главе IV
1. Единственность решения. 2. Представление бигармонических функций через гармонические функции. 3. Решение бигармонического уравнения для круга.
Глава V. Распространение волн в пространстве
1. Уравнение колебаний в пространстве. 2. Метод усреднения. 3. Формула Пуассона. 4. Метод спуска. 5. Физическая интерпретация. 6. Метод отражения.
1. Вывод интегральной формулы. 2. Следствия из интегральной формулы.
1. Общая схема метода разделения переменных. Стоячие волны. 2. Колебания прямоугольной мембраны. 3. Колебания круглой мембраны. Задачи к главе V
Приложения к главе V
1. Уравнения электромагнитного поля и граничные условия. 2. Потенциалы электромагнитного поля. 3. Электромагнитное поле осциллятора.
Глава VI. Распространение тепла в пространстве
1. Функция температурного влияния. 2. Распространение тепла в неограниченном пространстве.
1. Схема метода разделения переменных. 2. Остывание круглого цилиндра. 3. Определение критических размеров.
1. Формула Грина дли уравнения теплопроводности и функция источника. 2. Решение краевой задачи. 3. Функция источника для отрезка.
1. Свойства тепловых потенциалов простого и двойного слоя. 2. Решение краевых задач. Задачи к главе VI
Приложения к главе VI
Глава VII. Уравнения эллиптического типа (продолжение)
1. Установившиеся колебания. 2. Диффузия газа при наличии распада и при цепных реакциях. 3. Диффузия в движущейся среде. 4. Постановка внутренних краевых задач для уравнения D v + cv=0.
1. Функции влияния точечных источников. 2. Интегральное представление решения. 3. Потенциалы.
1. Уравнение D v + cv =-f в неограниченном пространстве. 2. Принцип предельного поглощения. 3. Принцип предельной амплитуды. 4. Условия излучения.
1. Постановка задачи. 2. Единственность решения задачи дифракции. 3. Дифракция на сфере. Задачи к главе VII
Приложения к главе VII
1. Собственные колебания цилиндрического эндовибратора. 2. Электромагнитная энергия собственных колебаний. 3. Возбуждение колебаний в эндовибраторе.
Дополнение I. Метод конечных разностей
1. Сетки и сеточные функции. 2. Аппроксимация простейших дифференциальных операторов. 3. Разностная задача. 4. Устойчивость.
1. Схемы для уравнения с постоянными коэффициентами. 2. Погрешность аппроксимации. 3. Энергетическое тождество. 4. Устойчивость. 5. Сходимость и точность. 6. Разностные схемы для уравнений с переменными коэффициентами. 7. Метод баланса. Консервативные схемы. 8. Двухслойные схемы для уравнения теплопроводности с переменными коэффициентами. 9. Трехслойные схемы. 10. Решение систем разностных уравнений. Метод прогонки. 11. Разностные методы решения квазилинейных уравнений.
1. Разностная аппроксимация оператора Лапласа. 2. Принцип максимума. 3. Оценка решения неоднородного уравнения. 4. Сходимость решения разностной задачи Дирихле. 5. Решение разностных уравнений методом простой итерации.
1. Многомерные схемы. 2. Экономичные схемы. 3. Итерационные методы переменных направлений для решения разностной задачи Дирихле.
Дополнение II. Специальные функции
1. Введение. 2. Общее уравнение теории специальных функций. 3. Поведение решений в окрестности х=а, если k(а)=0. 4. Постановка краевых задач.
Часть I. Цилиндрические функции
1. Степенные ряды. 2. Рекуррентные формулы. 3. Функции полуцелого порядка. 4. Асимптотический порядок цилиндрических функций.
1. Функции Ханкеля. 2. Функции Ханкеля и Неймана. 3. Функции мнимого аргумента. 4. Функция K 0 (х).
1. Контурные интегралы. 2. функции Ханкеля. 3. Некоторые свойства гамма-функции. 4. Интегральное представление функции Бесселя. 5. Интегральное представление K n (х). 6, Асимптотические формулы для цилиндрических функций.
1. Многомерные схемы. 2. Экономичные схемы. 3. Итерационные методы переменных направлений для решения разностной задачи Дирихле.
Часть II. Сферические функции
1. Производящая функция и полиномы Лежандра. 2. Рекуррентные формулы. 3. Уравнение Лежандра. 4. Ортогональность полиномов Лежандра. 5. Норма полиномов Лежандра. 6. Нули полиномов Лежандра. 7. Ограниченность полиномов Лежандра.
1. Присоединенные функции. 2. Норма присоединенных функций. 3. Замкнутость системы присоединенных функций.
1. Гармонические полиномы. 2. Сферические функции. 3. Ортогональность системы сферических функции. 4. Полнота системы сферических функций. 5. Разложение по сферическим функциям.
1. Задача Дирихле для сферы. 2. Проводящая сфера в поле точечного заряда. 3. Поляризация шара в однородном поле. 4. Собственные колебания сферы. 5. Внешняя краевая задача для сферы.
Часть III. Полиномы Чебышева — Эрмита и Чебышева — Лагерра
1. Дифференциальная формула. 2. Рекуррентные формулы. 3. Уравнение Чебышева — Эрмита. 4. Норма полиномов Нn(x). 5. Функции Чебышева — Эрмита.
1. Дифференциальная формула. 2. Рекуррентные формулы. 3. Уравнение Чебышева —Лагерра. 4. Ортогональность и норма полиномов Чебышева—Лагерра. 5. Обобщенные полиномы Чебышева —Лагерра.
1. Уравнение Шредингера. 2. Гармонический осциллятор. 3. Ротатор. 4. Движение электрона в кулоновом поле.
Максвелл ввел понятие полного тока,равного сумме токов проводимости (а также конвекционных токов) и смещения.Плотность полного тока 1 страница
Введя понятия тока смещения и полного тока, Максвелл по-новому подошел к рассмотрению замкнутости цепей переменного тока. Полный ток в них всегда замкнут, т. е. на концах проводника обрывается лишь ток проводимости, а в диэлектрике (вакууме) между концами проводника имеется ток смещения, который замыкает ток проводимости.
Максвелл обобщил теорему о циркуляции вектора Н (см. (133.10)), введя в ее правую часть полный ток Iполн =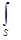 
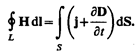
jполнdS сквозь поверхность S, натянутую на замкнутый контур L. Тогдаобобщенная теорема о циркуляции вектора Н запишется в виде
(138.4)
Выражение (138.4) справедливо всегда, свидетельством чего является полное соответствие теории и опыта.
§ 139. Уравнения Максвелла для электромагнитного поля
Введение Максвеллом понятия тока смещения привело его к завершению созданной им макроскопической теории электромагнитного поля, позволившей с единой точки зрения не только объяснить электрические и магнитные явления, но и предсказать новые, существование которых было впоследствии подтверждено.
В основе теории Максвелла лежат рассмотренные выше четыре уравнения:
1. Электрическое поле (см. § 137) может быть как потенциальным (ЕQ), так и вихревым (ЕB), поэтому напряженность суммарного поля Е=ЕQ +ЕB. Так как циркуляция вектора ЕQ равна нулю (см. (137.3)), а циркуляция вектора ЕB определяется выражением (137.2), то циркуляция вектора напряженности суммарного поля
Это уравнение показывает, что источниками электрического поля могут быть не только электрические заряды, но и изменяющиеся во времени магнитные поля.
2. Обобщенная теорема о циркуляции вектора Н (см. (138.4)):
Это уравнение показывает, что магнитные поля могут возбуждаться либо движущимися зарядами (электрическими токами), либо переменными электрическими полями.
3. Теорема Гаусса для поля D (см. (89.3)):
(139.1)
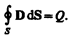
Если заряд распределен внутри замкнутой поверхности непрерывно с объемной плотностью r, то формула (139.1) запишется в виде
4. Теорема Гаусса для поля В (см. (120.3)):
Итак, полная система уравнений Максвелла в интегральной форме:
Величины, входящие в уравнения Максвелла, не являются независимыми и между ними существует следующая связь (изотропные несегнетоэлектрические и неферромагнитные среды):
где e0 и m0 — соответственно электрическая и магнитная постоянные, e и m — соответственно диэлектрическая и магнитная проницаемости, g — удельная проводимость вещества.
Из уравнений Максвелла вытекает, что источниками электрического поля могут быть либо электрические заряды, либо изменяющиеся во времени магнитные поля, а магнитные поля могут возбуждаться либо движущимися электрическими зарядами (электрическими токами), либо переменными электрическими полями. Уравнения Максвелла не симметричны относительно электрического и магнитного полей. Это связано с тем, что в природе существуют электрические заряды, но нет зарядов магнитных.
Для стационарных полей (E=const и B=const) уравнения Максвелла примут вид
т.е. источниками электрического поля в данном случае являются только электрические заряды, источниками магнитного — только токи проводимости. В данном случае электрические и магнитные поля независимы друг от друга, что и позволяет изучать отдельно постоянные электрическое и магнитное поля.
Воспользовавшись известными из векторного анализа теоремами Стокса и Гаусса
можно представить полную систему уравнении Максвелла в дифференциальном форме (характеризующих поле в каждой точке пространства):
Если заряды и токи распределены в пространстве непрерывно, то обе формы уравнений Максвелла — интегральная и дифференциальная — эквивалентны. Однако если имеются поверхности разрыва – поверхности, на которых свойства среды или полей меняются скачкообразно, то интегральная форма уравнений является более общей.
Уравнения Максвелла в дифференциальной форме предполагают, что все величины в пространстве и времени изменяются непрерывно. Чтобы достичь математической эквивалентности обеих форм уравнений Максвелла, дифференциальную форму дополняют граничными условиями, которым должно удовлетворять электромагнитное поле на границе раздела двух сред. Интегральная форма уравнений Максвелла содержит эти условия. Они были рассмотрены раньше (см. § 90, 134):
(первое и последнее уравнения отвечают случаям, когда на границе раздела нет ни свободных зарядов, ни токов проводимости).
Уравнения Максвелла — наиболее общие уравнения для электрических и магнитных полей в покоящихся средах. Они играют в учении об электромагнетизме такую же роль, как законы Ньютона в механике. Из уравнений Максвелла следует, что переменное магнитное поле всегда связано с порождаемым им электрическим полем, а переменное электрическое поле всегда связано с порождаемым им магнитным, т. е. электрическое и магнитное поля неразрывно связаны друг с другом — они образуют единое электромагнитное поле.
Теория Максвелла, являясь обобщением основных законов электрических и магнитных явлений, не только смогла объяснить уже известные экспериментальные факты, что также является важным ее следствием, но и предсказала новые явления. Одним из важных выводов этой теории явилось существование магнитного поля токов смещения (см. § 138), что позволило Максвеллу предсказать существование электромагнитных волн — переменного электромагнитного поля, распространяющегося в пространстве с конечной скоростью. В дальнейшем было доказано, что скорость распространения свободного электромагнитного поля (не связанного с зарядами и токами) в вакууме равна скорости света с = 3×10 8 м/с. Этот вывод и теоретическое исследование свойств электромагнитных волн привели Максвелла к созданию электромагнитной теории света, согласно которой свет представляет собой также электромагнитные волны. Электромагнитные волны на опыте были получены немецким физиком Г. Герцем (1857—1894), доказавшим, что законы их возбуждения и распространения полностью описываются уравнениями Максвелла. Таким образом, теория Максвелла была экспериментально подтверждена.
К электромагнитному полю применим только принцип относительности Эйнштейна, так как факт распространения электромагнитных волн в вакууме во всех системах отсчета с одинаковой скоростью с не совместим с принципом относительности Галилея.
Согласно принципу относительности Эйнштейна, механические, оптические и электромагнитные явления во всех инерциальных системах отсчета протекают одинаково, т. е. описываются одинаковыми уравнениями. Уравнения Максвелла инвариантны относительно преобразований Лоренца: их вид не меняется при переходе от одной инерциальной системы отсчета к другой, хотя величины Е, В, D, Н в них преобразуются по определенным правилам.
Из принципа относительности вытекает, что отдельное рассмотрение электрического и магнитного полей имеет относительный смысл. Taк, если электрическое поле создается системой неподвижных зарядов, то эти заряды, являясь неподвижными относительно одной инерциальной системы отсчета, движутся относительно другой и, следовательно, будут порождать не только электрическое, но и магнитное поле. Аналогично, неподвижный относительно одной инерциальной системы отсчета проводник с постоянным током, возбуждая в каждой точке пространства постоянное магнитное поле, движется относительно других инерциальных систем, и создаваемое им переменное магнитное поле возбуждает вихревое электрическое поле.
Таким образом, теория Максвелла, ее экспериментальное подтверждение, а также принцип относительности Эйнштейна приводят к единой теории электрических, магнитных и оптических явлений, базирующейся на представлении об электромагнитном поле.
4 КОЛЕБАНИЯ И ВОЛНЫ
Глава 18 Механические и электромагнитные колебания
§ 140. Гармонические колебания и их характеристики
Колебаниями называются движения или процессы, которые характеризуются определенной повторяемостью во времени. Колебательные процессы широко распространены в природе и технике, например качание маятника часов, переменный электрический ток и т. д. При колебательном движении маятника изменяется координата его центра масс, в случае переменного тока колеблются напряжение и ток в цепи. Физическая природа колебаний может быть разной, поэтому различают колебания механические, электромагнитные и др. Однако различные колебательные процессы описываются одинаковыми характеристиками и одинаковыми уравнениями. Отсюда следует целесообразность единого подхода к изучению колебаний различной физической природы. Например, единый подход к изучению механических и электромагнитных колебаний применялся английским физиком Д. У. Рэлеем (1842—1919), А. Г. Столетовым, русским инженером-экспериментатором П. Н. Лебедевым (1866—1912). Большой вклад в развитие теории колебаний внесли Л. И. Мандельштам (1879—1944) и его ученики.
Колебания называютсясвободными (илисобственными), если они совершаются за счет первоначально сообщенной энергии при последующем отсутствии внешних воздействий на колебательную систему (систему, совершающую колебания). Простейшим типом колебаний являютсягармонические колебания — колебания, при которых колеблющаяся величина изменяется со временем по закону синуса (косинуса). Рассмотрение гармонических колебаний важно по двум причинам: 1) колебания, встречающиеся в природе и технике, часто имеют характер, близкий к гармоническому; 2) различные периодические процессы (процессы, повторяющиеся через равные промежутки времени) можно представить как наложение гармонических колебаний. Гармонические колебания величины s описываются уравнением типа
(140.1)
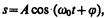
где А — максимальное значение колеблющейся величины, называемоеамплитудой колебания, w0 —круговая (циклическая) частота, j —начальная фаза колебания в момент времени t=0, (w0t+j) — фаза колебания в момент времени t. Фаза колебания определяет значение колеблющейся величины в данный момент времени. Так как косинус изменяется в пределах от +1 до –1, то s может принимать значения от +А до –А.
Определенные состояния системы, совершающей гармонические колебания, повторяются через промежуток времени Т, называемыйпериодом колебания, за который фаза колебания получает приращение 2p, т. е.
(140.2)
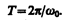
Величина, обратная периоду колебаний,
(140.3)
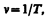
т. е. число полных колебаний, совершаемых в единицу времени, называется частотой колебаний. Сравнивая (140.2) и (140.3), получим
Единица частоты —герц (Гц): 1 Гц — частота периодического процесса, при которой за 1 с совершается один цикл процесса.
Запишем первую и вторую производные по времени от гармонически колеблющейся величины s:
(140.4)
(140.5)
т. е. имеем гармонические колебания с той же циклической частотой. Амплитуды величин (140.4) и (140.5) соответственно равны Аw0 и Аw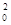 
. Фаза величины (140.4) отличается от фазы величины (140.1) на p/2, а фаза величины (140.5) отличается от фазы величины (140.1) на p. Следовательно, в моменты времени, когда s=0, ds/dt приобретает наибольшие значения; когда же s достигает максимального отрицательного значения, то d 2 s/dt 2 приобретает наибольшее положительное значение (рис. 198).
Из выражения (140.5) следуетдифференциальное уравнение гармонических колебаний
(140.6)
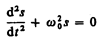
(где s = A cos (w0t+j)). Решением этого уравнения является выражение (140.1).
Гармонические колебания изображаются графическиметодом вращающегося вектора амплитуды,илиметодом векторных диаграмм. Для этого из произвольной точки О, выбранной на оси х, под углом j, равным начальной фазе колебания, откладывается вектор А, модуль которого равен амплитуде А рассматриваемого колебания (рис. 199). Если этот вектор привести во вращение с угловой скоростью w0, равной циклической частоте колебаний, то проекция конца вектора будет перемещаться по оси х и принимать значения от –А до +А, а колеблющаяся величина будет изменяться со временем по закону s=A cos (w0t+j). Таким образом, гармоническое колебание можно представить проекцией на некоторую произвольно выбранную ось вектора амплитуды А, отложенного из произвольной точки оси под углом j, равным начальной фазе, и вращающегося с угловой скоростью w0 вокруг этой точки.
В физике часто применяется другой метод, который отличается от метода вращающегося вектора амплитуды лишь по форме. В этом методе колеблющуюся величину представляюткомплексным числом. Согласно формуле Эйлера, для комплексных чисел
(140.7)
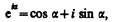
где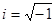 
— мнимая единица. Поэтому уравнение гармонического колебания (140.1) можно записать в комплексной форме:
(140.8)
Вещественная часть выражения (140.8)
представляет собой гармоническое колебание. Обозначение Re вещественной части условимся опускать и (140.8) будем записывать в виде
В теории колебаний принимается, что колеблющаяся величина s равна вещественной части комплексного выражения, стоящего в этом равенстве справа.
§ 141. Механические гармонические колебания
Пусть материальная точка совершает прямолинейные гармонические колебания вдоль оси координат х около положения равновесия, принятого за начало координат. Тогда зависимость координаты х от времени t задается уравнением, аналогичным уравнению (140.1), где s=x:
(141.1)
Согласно выражениям (140.4) в (140.5), скорость v и ускорение а колеблющейся точки соответственно равны
(141.2)
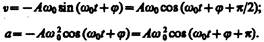
Сила F=ma, действующая на колеблющуюся материальную точку массой т, с учетом (141.1) и (1412) равна
Следовательно, сила пропорциональна смещению материальной точки из положения равновесия и направлена в противоположную сторону (к положению равновесия).
Кинетическая энергия материальной точки, совершающей прямолинейные гармонические колебания, равна
(141.3)
(141.4)
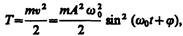
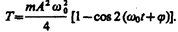
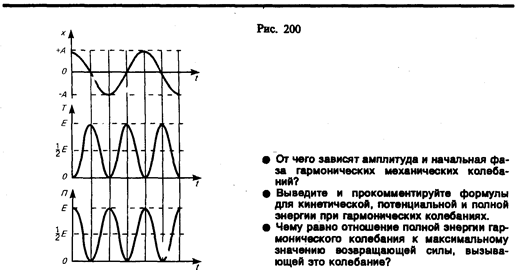
Потенциальная энергияматериальной точки, совершающей гармонические колебания под действием упругой силы F, равна
(141.5)
(141.6)
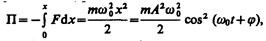
Сложив (141.3) и (141.5), получим формулу дляполной энергии:
(141.7)
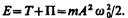
Полная энергия остается постоянной, так как при гармонических колебаниях справедлив закон сохранения механической энергии, поскольку упругая сила консервативна.
Из формул (141.4) и (141.6) следует, что Т и П изменяются с частотой 2w0, т. е. с частотой, которая в два раза превышает частоту гармонического колебания. На рис. 200 представлены графики зависимости x, T и П от времени. Так как ásin 2 añ = ácos 2 añ = 1/2, то из формул (141.3), (141.5) и (14l.7) следует, что áTñ = áПñ = ½ E.
§ 142. Гармонический осциллятор. Пружинный, физический и математический маятники
Гармоническим осциллятором называется система, совершающая колебания, описываемые уравнением вида (140.6);
(142.1)
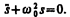
Колебания гармонического осциллятора являются важным примером периодического движения и служат точной или приближенной моделью во многих задачах классической и квантовой физики. Примерами гармонического осциллятора являются пружинный, физический и математический маятники, колебательный контур (для токов и напряжений столь малых, что элементы контура можно было бы считать линейными; см. §146).
1. Пружинный маятник — это груз массой т, подвешенный на абсолютно упругой пружине и совершающий гармонические колебания под действием упругой силы F = –kx, где k —жесткость пружины. Уравнение движения маятника
Из выражений (142.1) и (140.1) следует, что пружинный маятник совершает гармонические колебания по закону х=А соs (w0t + j) с циклической частотой
(142.2)
(142.3)
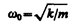
Формула (142.3) справедлива для упругих колебаний в пределах, в которых выполняется закон Гука (см. (21.3)), т. е. когда масса пружины мала по сравнению с массой тела. Потенциальная энергия пружинного маятника, согласно (141.5) и (142.2), равна
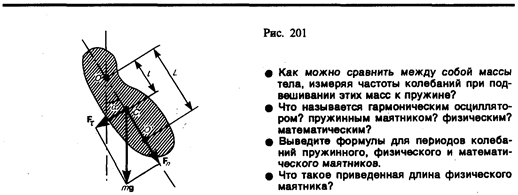
2. Физический маятник — это твердое тело, совершающее под действием силы тяжести колебания вокруг неподвижной горизонтальной оси, проходящей через точку О, не совпадающую с центром масс С тела (рис. 201).
Если маятник отклонен из положения равновесия на некоторый угол a, то в соответствии с уравнением динамики вращательного движения твердого тела (18.3) момент M возвращающей силы можно записать в виде
(142.4)
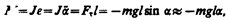
где J — момент инерции маятника относительно оси, проходящей через точку подвеса О, l – расстояние между ней и центром масс маятника, Ft= –mg sina » –mga. — возвращающая сила (знак минус обусловлен тем, что направления Ft и a всегда противоположны; sina »a соответствует малым колебаниям маятника, т.е. малым отклонениям маятника из положения равновесия). Уравнение (142.4) можно записать в виде
(142.5)
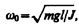
идентичное с (142.1), решение которого (140.1) известно:
(142.6)
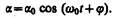
Из выражения (142.6) следует, что при малых колебаниях физический маятник совершает гармонические колебания с циклической частотой w0 (см. (142.5)) и периодом
(142.7)
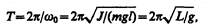
где L=J/(ml) —приведенная длина физического маятника.
Точка О’ на продолжении прямой ОС, отстоящая от точки О подвеса маятника на расстоянии приведенной длины L, называется центром качаний физического маятника (рис. 201). Применяя теорему Штейнера (16.1), получим
т. е. ОО’ всегда больше ОС. Точка подвеса О маятника и центр качаний О’ обладают свойством взаимозаменяемости: если точку подвеса перенести в центр качаний, то прежняя точка О подвеса
станет новым центром качаний, и период колебаний физического маятника не изменится.
3. Математический маятник — это идеализированная система, состоящая из материальной точки массой т, подвешенной на нерастяжимой невесомой нити, и колеблющаяся под действием силы тяжести. Хорошим приближением математического маятника является небольшой тяжелый шарик, подвешенный на тонкой длинной нити. Момент инерции математического маятника
(142.8)
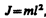
где l — длина маятника.
Так как математический маятник можно представить как частный случай физического маятника, предположив, что вся его масса сосредоточена в одной точке — центре масс, то, подставив выражение (142.8) в формулу (1417), получим выражение для периода малых колебаний математического маятника
(142.9)
Сравнивая формулы (142.7) и (142.9), видим, что если приведенная длина L физического маятника равна длине l математического маятника, то периоды колебаний этих маятников одинаковы. Следовательно, приведенная длина физического маятника — это длина такого математического маятника, период колебаний которого совпадает с периодом колебаний данного физического маятника.
§ 143. Свободные гармонические колебания в колебательном контуре
Среди различных электрических явлений особое место занимают электромагнитные колебания, при которых электрические величины (заряды, токи) периодически изменяются и которые сопровождаются взаимными превращениями электрического и магнитного полей. Для возбуждения и поддержания электромагнитных колебаний используетсяколебательный контур — цепь, состоящая из включенных последовательно катушки индуктивностью L, конденсатора емкостью С и резистора сопротивлением R.
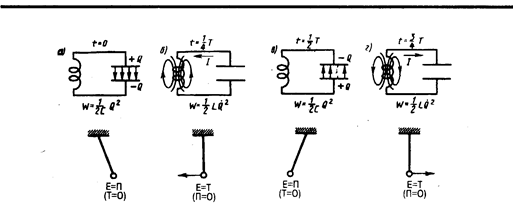
Рассмотрим последовательные стадии колебательного процесса в идеализированном контуре, сопротивление которого пренебрежимо мало (R»0). Для возбуждения в контуре колебаний конденсатор предварительно заряжают, сообщая его обкладкам заряды ±Q. Тогда в начальный момент времени t=0 (рис. 202, а) между обкладками конденсатора возникнет электрическое поле, энергия которого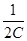 
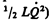
Q 2 (см. (95.4)). Если замкнуть конденсатор на катушку индуктивности, он начнет разряжаться, и в контуре потечет возрастающий со временем ток I. В результате энергия электрического поля будет уменьшаться, а энергия магнитного поля катушки (она равна 
— возрастать.
Так как R»0, то, согласно закону сохранения энергии, полная энергия
таккак она на нагревание не расходуется. Поэтому в момент t=¼T, когда конденсатор полностью разрядится, энергия электрического поля обращается в нуль, а энергия магнитного поля (а следовательно, и ток) достигает наибольшего значения (рис. 202, б). Начиная с этого момента ток в контуре будет убывать; следовательно, начнет ослабевать магнитное поле катушки, и в ней индуцируется ток, который течет (согласно правилу Ленца) в том же направлении, что и ток разрядки конденсатора. Конденсатор начнет перезаряжаться, возникнет электрическое поле, стремящееся ослабить ток, который в конце концов обратится в нуль, а заряд на обкладках конденсатора достигнет максимума (рис. 202, в). Далее те же процессы начнут протекать в обратном направлении (рис. 202, г) и система к моменту времени t=Т придет в первоначальное состояние (рис. 202, а). После этого начнется повторение рассмотренного цикла разрядки и зарядки конденсатора. Если бы потерь энергии не было, то в контуре совершались бы периодические незатухающие колебания, т.е. периодически изменялись (колебались) бы заряд Q на обкладках конденсатора, напряжение U на конденсаторе и сила тока I, текущего через катушку индуктивности. Следовательно, в контуре возникают электрические колебания, причем колебания сопровождаются превращениями энергий электрического и магнитного полей.
Электрические колебания в колебательном контуре можно сопоставить с механическими колебаниями маятника (рис. 202 внизу), сопровождающимися взаимными превращениями потенциальной и кинетической энергий маятника. В данном случае энергия электрического поля конденсатора (Q 2 /(2C)) аналогична потенциальной энергии маятника, энергия магнитного поля катушки (LQ 2 /2) — кинетической энергии, сила тока в контуре — скорости движения маятника. Индуктивность L играет роль массы т, а сопротивление контура — роль силы трения, действующей на маятник.
Согласно законуОма, для контура, содержащего катушку индуктивностью L, конденсатор емкостью С и резистор сопротивлением R,
где IR—напряжение на резисторе, Uc=Q/C—напряжение на конденсаторе, 
– э.д.с. самоиндукции, возникающая в катушке при протекании в ней переменного тока ( 
– единственная э.д.с. в контуре). Следовательно,
(143.1)
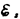
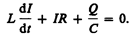
Разделив (143.1) на L и подставив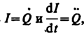 
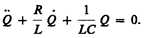
получим дифференциальное уравнение колебаний заряда Q в контуре:
(143.2)
В данном колебательном контуре внешние э.д.с. отсутствуют, поэтому рассматриваемые колебания представляют собой свободные колебания (см. §140). Если сопротивление R=0, то свободные электромагнитные колебания в контуре являются гармоническими. Тогда из (143.2) получим дифференциальное уравнение свободных гармонических колебаний заряда в контуре.
Лекция №7. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ
5.1. Свободные гармонические колебания и их характеристики.
Колебания − это движения или процессы, обладающие той или иной степенью повторяемости во времени. Колебания называются периодическими, если значения физических величин, изменяющихся в процессе колебания, повторяются через равные промежутки времени. Наиболее важными характеристиками колебания являются: смещение, амплитуда, период, частота, циклическая частота, фаза.
Простейший вид периодических колебаний − это гармонические колебания. Гармонические колебания − это периодическое изменение во времени физической величины, происходящее по закону косинуса или синуса. Уравнение гармонических колебаний имеет вид
1) Смещение x − это величина, характеризующая колебания и равная отклонению тела от положения равновесия в данный момент времени.
2) Амплитуда колебаний А − это величина, равная максимальному отклонению тела от положения равновесия.
3) Период колебаний T − это наименьший промежуток времени, через который система, совершающая колебания, снова возвращается в то же состояние, в котором она находилась в начальный момент, выбранный произвольно. Единица измерения [T] = 1 с .
За период система совершает одно полное колебание.
4) Частота колебаний ν − это величина, равная числу колебаний, совершаемых в единицу времени (за 1 секунду). Единица измерения [ν]= 1 Гц . Частота определяется по формуле
5) Циклическая частота ω − это величина, равная числу полных колебаний, совершающихся за 2π секунд. За единицу циклической частоты принята угловая частота, при которой за время 1 с совершается 2π циклов колебаний, [ω]= с -1 . Циклическая частота связана с периодом и частотой колебаний соотношением
6) Фаза колебаний ωt + φ0 − фаза указывает местоположение колеблющейся точки в данный момент времени.
7) Начальная фаза φ0 − указывает местоположение колеблющейся точки в момент времени t = 0 .
5.2. Сложение одинаково направленных и взаимно перпендикулярных гармонических колебаний.
Сложение нескольких колебаний одинакового направления можно изображать графически с помощью метода векторной диаграммы.
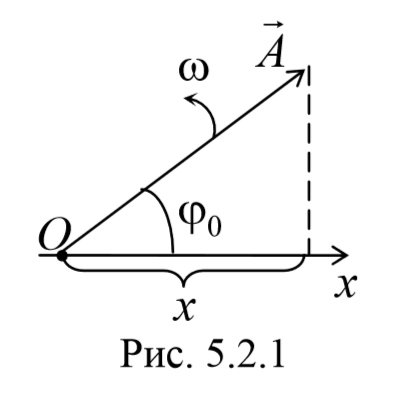
Гармоническое колебание может быть представлено графически с помощью вращающегося вектора амплитуды А . Для этого из произвольной точки O , выбранной на оси Ox , под углом φ0 , равным начальной фазе колебания, откладывается вектор амплитуды А . Модуль этого вектора равен амплитуде рассматриваемого колебания. Если этот вектор привести во вращение с угловой скоростью ω , равной циклической частоте колебаний, то проекция конца вектора амплитуды будет перемещаться по оси Ox и принимать значения от -A до +A , а колеблющаяся величина изменяться со временем по закону x = Acos(ωt + φ0)
1. Сложение одинаково направленных гармонических колебаний.
Сложим два гармонических колебания одинакового направления и одинаковой частоты. Смещение x колеблющегося тела будет суммой смещений x1 и x2 , которые запишутся следующим образом:
Представим оба колебания на векторной диаграмме. Построим по правилу сложения векторов результирующий вектор А . Проекция этого вектора на ось Ox равна сумме проекций слагаемых векторов x=x2+x2 , следовательно, вектор А представляет собой результирующее колебание. Определим результирующий вектор амплитуды А потеореме косинусов
Так как угол между векторами А 1 и А 2 равен φ=π-(φ2-φ1) , то cos[π-(φ2-φ1)]=-cos(φ2-φ1) , следовательно, результирующая амплитуда колебания будет равна
Определим начальную фазу результирующего колебания.
Из рисунка видно, что начальная фаза результирующего колебания
Таким образом, тело, участвуя в двух гармонических колебаниях одного направления и одинаковой частоты, также совершает гармонические колебания в том же направлении и с той же частотой.
2. Сложение взаимно перпендикулярных гармонических колебаний.
Рассмотрим результат сложения двух гармонических колебаний одинаковой частоты, происходящих во взаимно перпендикулярных направлениях. Допустим, что материальная точка совершает колебания как вдоль оси X , так и вдоль оси Y . Выберем начало отсчета времени так, чтобы начальная фаза первого колебания была равна нулю. Тогда уравнения колебаний примут вид
где φ − разность фаз обоих колебаний.
Уравнение траектории получим, исключив из уравнений (5.2.6) параметр времени t: cosωt= $$x\over A_1$$ , а sinωt= $$\sqrt<1-cos^2 ωt>=\sqrt<1-x^2\over A_1^2>$$ Разложим косинус во втором из уравнений (5.2.6)
Перепишем это уравнение в следующем виде
После преобразования, получим
Используя тригонометрическое тождество cos 2 φ+sin 2 φ=1 , окончательно получим
Это есть уравнение эллипса, оси которого ориентированы относительно координатных осей произвольно. Ориентация эллипса и величина его полуосей зависят от амплитуд колебаний и разности фаз.
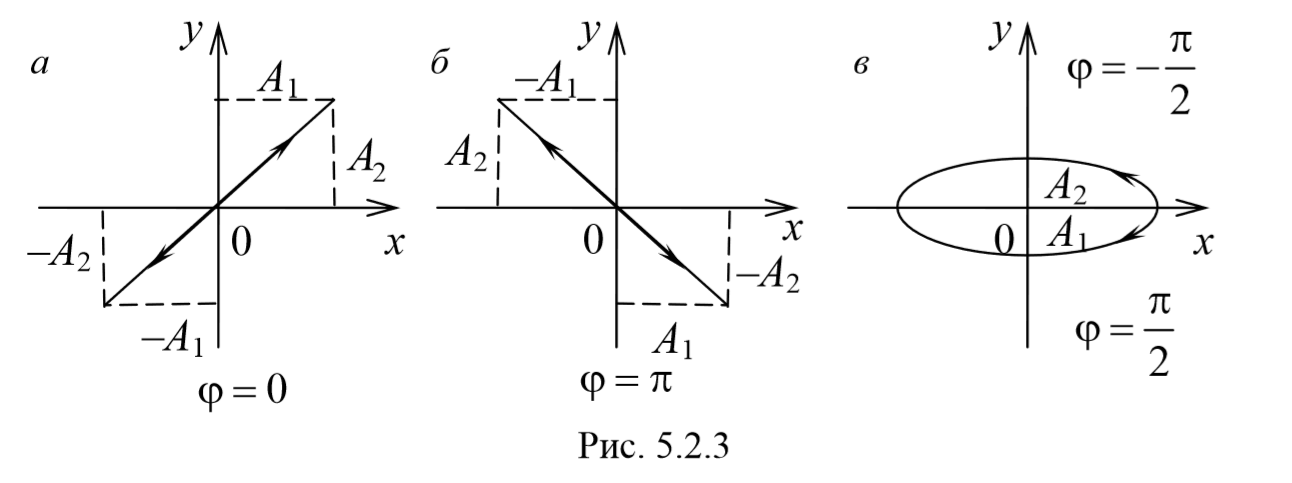
Рассмотрим несколько частных случаев и определим форму траектории для них:
a) разность фаз равна нулю [φ=0]
В этом случае $$( < x\over A_1 >— < y\over A_2 >)^2=0$$ , откуда получается уравнение прямой
Результирующее движение является гармоническим колебанием вдоль этой прямой с частотой ω и амплитудой $$A= \sqrt
2) разность фаз равна ±π[φ=±π] .
В этом случае $$( < x\over A_1 >— < y\over A_2 >)^2=0$$ , откуда получается уравнение прямой
3) Разность фаз равна ± $$π\over 2$$ [φ=± $$π \over2$$ ] . Тогда
Уравнение эллипса, причем полуоси эллипса равны соответствующим амплитудам колебаний. При равенстве амплитуд колебаний эллипс вырождается в окружность. Случаи φ=+ $$π\over 2$$ и φ=- $$π\over 2$$ отличаются направлением движения. Если φ=+ $$π\over 2$$ , то уравнения колебаний имеют следующий вид: x=A1cosωt , и y=-A2sinωt и движение совершается по часовой стрелке. Если φ=- $$π\over 2$$ , , то уравнения колебаний имеют следующий вид: x=A1cosωt , и y=A2sinωt и движение совершается против часовой стрелке.
Рассмотренные три частных случая представлены на рис. 5.2.3, а, б, в. Рис
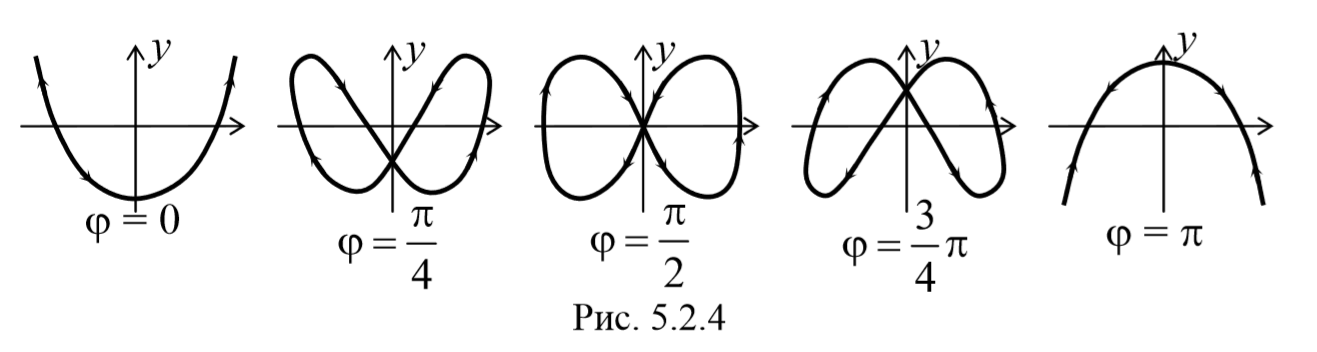
4) Если частоты складываемых взаимно перпендикулярных колебаний различны, то траектория результирующего движения имеет вид сложных кривых, называемых фигурами Лиссажу . Форма этих кривых определяется соотношением амплитуд, частот и разности фаз складываемых колебаний.
На рис. 5.2.4 показаны фигуры Лиссажу, которые получаются при соотношении частот 1:2 и различной разности фаз колебаний.
По виду фигур можно определить неизвестную частоту по известной частоте или определить соотношение частот складываемых колебаний.
5.3. Дифференциальное уравнение гармонических колебаний и его решение.
Продифференцируем по времени уравнение гармонических колебаний
и получим выражение для скорости
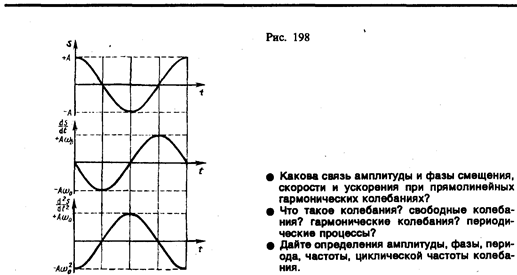
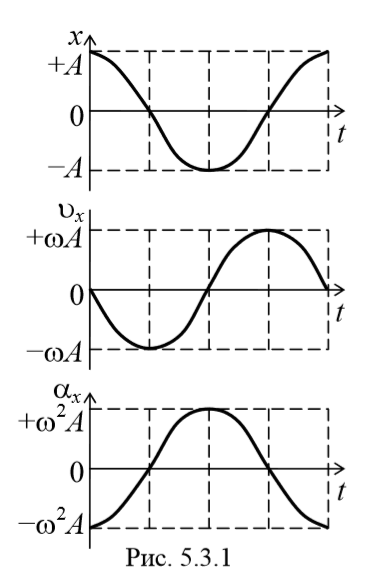
Из сравнения уравнений (5.3.1) и (5.3.2) следует, что скорость опережает смещение по фазе на π/2 . Амплитуда скорости равна Аω .
Продифференцировав уравнение (2) еще раз по времени, получим выражение для ускорения
Как следует из уравнения (5.3.3), ускорение и смещение находятся в противофазе. Это означает, что в тот момент времени, когда смещение достигает наибольшего, положительного значения, ускорение достигает наибольшего по величине отрицательного значения, и наоборот. Амплитуда ускорения равна Аω 2 (рис. 5.3.1).
Из выражения (5.3.3) следует дифференциальное уравнение гармонических колебаний
Результирующая сила, действующая на материальную точку массой m , определяется с помощью второго закона Ньютона. Проекция этой силы
Эта сила пропорциональна смещению точки из положения равновесия и направлена в сторону противоположную этому смещению, т. е. она стремится вернуть точку в положение равновесия, и поэтому называется возвращающей силой . Таким образом, гармонические колебания происходят под действием силы F , пропорциональной смещению x и направленной к положению равновесия,
где k=mω 2 − постоянный коэффициент. Возвращающая сила подобна упругим силам, возникающим в телах при их деформации. Такая зависимость силы от смещения характерна для упругой силы, поэтому силы иной физической природы, удовлетворяющие зависимости (5.3.6) называются квазиупругими силами .
Материальная точка, совершающая колебания под действием квазиупругой силы, называется линейным осциллятором . Ее динамическое поведение описывается дифференциальным уравнением
ω0 − собственная частота осциллятора.
Решение этого уравнения дает закон движения линейного осциллятора x=Acos(ωt+φ0) .
5.4. Энергия гармонических колебаний.
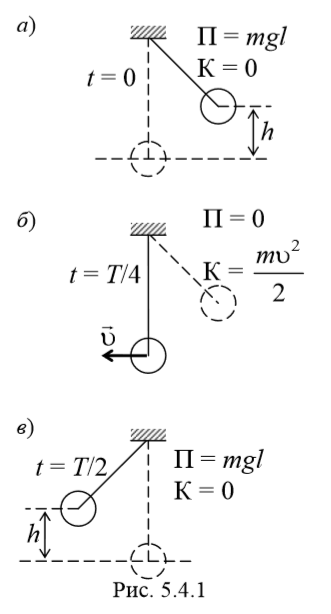
В процессе колебаний происходит превращение кинетической энергии в потенциальную энергию и обратно (рис. 5.4.1). В момент наибольшего отклонения от положения равновесия полная энергия состоит только из потенциальной энергии, которая достигает своего наибольшего значения. Далее при движении к положению равновесия потенциальная энергия уменьшается, при этом кинетическая энергия возрастает. При прохождении через положение равновесия полная энергия состоит лишь из кинетической энергии, которая в этот момент достигает своего наибольшего значения. Далее при движении к точке наибольшего отклонения происходит уменьшение кинетической и увеличение потенциальной энергии. И при наибольшем отклонении потенциальная опять максимальная, а кинетическая энергия рана нулю. И т. д.
Потенциальная энергия тела, совершающего гармонические колебания равна
Кинетическая энергия тела, совершающего гармонические колебания равна
Таким образом, полная энергия гармонического колебания, состоящая из суммы кинетической и потенциальной энергий, определяется следующим образом
Следовательно, полная энергия гармонического колебания
оказывается постоянной в случае гармонических колебаний.
Найдем среднее значение потенциальной энергии за период колебания
Аналогично получается для среднего значение кинетической энергии
Таким образом, и потенциальная, и кинетическая энергии изменяются относительно своих средних значений по гармоническому закону с частотой 2ω и амплитудой ωt kA 2
5.5. Пружинный, математический и физический маятники.
Рассмотрим несколько простейших систем, совершающих свободные гармонические колебания.
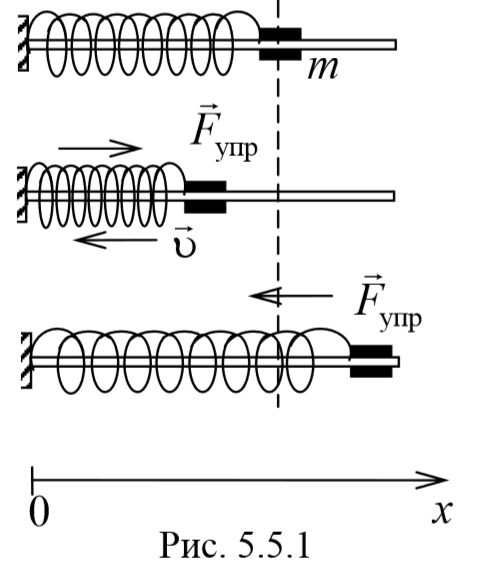
1) Пружинный маятник − это материальная точка массой m , подвешенная (или расположенная горизонтально) на абсолютно упругой пружине жесткостью k и совершающий гармонические колебания под действием упругой силы. Пусть шайба массой m , прикрепленная к пружине, совершает колебания. Для составления дифференциального уравнения колебаний запишем второй закон Ньютона в проекции на ось Ox Fупр=ma . Упругая сила Fупр=-kx . Приравнивая последние два уравнения и, используя определение ускорения тела, получим
Сравнивая уравнения (5.3.7) и (5.5.2) получаем, что пружинный маятник совершает гармонические колебания с частотой
Так как период колебаний определяется по формуле T= $$2π\over ω_0$$ , то период колебаний пружинного маятника
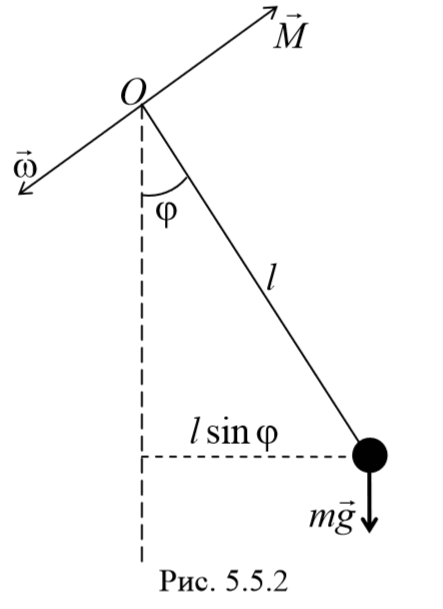
2) Математический маятник − это идеализированная система, состоящая из невесомой и нерастяжимой нити, на которой подвешена материальная точка массой m . Отклонение маятника от положения равновесия будем характеризовать углом φ , образованным нитью с вертикалью.
При отклонении маятника от положения равновесия возникает вращательный момент M , равный по величине mqlsinφ .Он имее акое же направление, что стремится вернуть маятник в положение равновесия. Следовательно, выражение для вращательного момента имеет вид: M=-mqlsinφ . Применим основно ательного движения
где L=ml 2 − момент инерции материальной точки. Тогда, учитывая, что угловое ускорение ε= $$d^2φ\over dt^2$$ , получим
Если рассматривать малые колебания, то sinφ≈φ . Получим
То есть при малых колебаниях угловое отклонение математического маятника изменяется по гармоническому закону с частотой
Период колебаний математического маятника
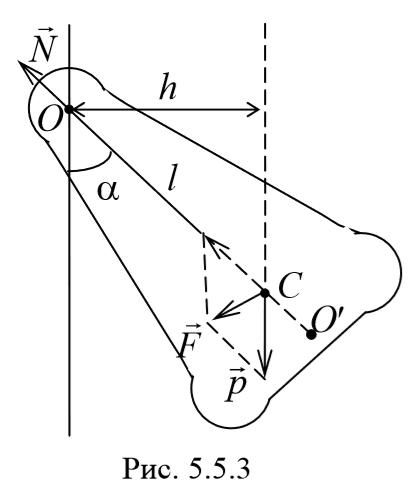
3) Физический маятник − это твердое тело, совершающее под действием силы тяжести колебания вокруг неподвижной оси, проходящей через точку, не совпадающую с центром масс тела. При отклонении маятника от положения равновесия на угол φ возникает вращательный момент, стремящийся вернуть маятник в положение равновесия. Этот момент равен M=-mglsinφ .
Согласно основному уравнению динамики вращательного движения получаем
где I − момент инерции маятника относительно оси, проходящей через точку подвеса.
Если рассматривать малые колебания, то sinφ≈φ . Получим
То есть при малых колебаниях угловое отклонение математического маятника изменяется по гармоническому закону с частотой
Период колебаний математического маятника
Из сопоставления формул периодов колебаний математического и физического маятников T=2π $$\sqrt
будет иметь такой же период колебаний, что и данный физический маятник.
Величина lпр (отрезок OO′) называется приведенной длиной физического маятника − это длина такого математического маятника, период колебаний которого совпадает с периодом данного физического маятника. Точка на прямой, соединяющей точку подвеса с центром масс, и лежащая на расстоянии приведенной длины от оси вращения, называется центром качания (О′) физического маятника. Точка подвеса О и центр качания обладают свойством взаимности: при переносе точки подвеса в центр качания прежняя точка подвеса становится новым центром качания.
http://helpiks.org/3-64414.html
http://physics.belstu.by/mechanics_lk/mechanics_lk7.html