Уравнение количества движения для газа

Кратко о гидродинамике: уравнения движения

Написав предыдущий пост, исторический и отчасти рекламный (хотя потенциальные абитуриенты такое вряд ли читают), можно перейти и к разговору «по существу». К сожалению, высокой степени популярности описания добиться вряд ли получится, но всё же постараюсь не устраивать курс сухих лекций. Хотя, от сухости избавиться не удалось, да и пост писался в результате ровно месяц.

В нынешней публикации описаны основные уравнения движения идеальной и вязкой жидкости. По возможности кратко рассмотрен их вывод и физический смысл, а также описаны несколько простейших примеров их точных решений. Увы, этими несколькими примерами доступные аналитически решения уравнений Навье-Стокса в значительной мере исчерпываются. Напомню, что Институт Клэя отнёс доказательство существования и гладкости решений к проблемам тысячелетия. Гении уровня Перельмана и выше — задача вас ждёт.

Понятие сплошной среды

В, если можно так выразиться, «традиционной» гидродинамике, сложившейся исторически, фундаментом является модель сплошной среды. Она отвлекается от молекулярной структуры вещества, и описывает среду несколькими непрерывными полевыми величинами: плотностью, скоростью (определяемой через суммарный импульс молекул в заданном элементе объёма) и давлением. Модель сплошной среды предполагает, что в любом бесконечно малом объёме содержится ещё достаточно много частиц (как принято говорить, термодинамически много — числа, близкие по порядку величины к числу Авогадро — 10 23 шт.). Таким образом, модель ограничена снизу дискретностью молекулярной структуры жидкости, что в задачах типичных пространственных масштабов совершенно несущественно.

Однако, такой подход позволяет описать не только воду в пробирке или водоёме, и оказывается куда более универсальным. Поскольку наша Вселенная на больших масштабах практически однородна, то, как ни странно, она начиная с некоторого масштаба превосходно описывается как сплошная среда, с учётом, конечно же, самогравитации.

Другими, более приземлёнными применениями сплошной среды являются описание свойств упругих тел, динамики плазмы, сыпучих тел. Также можно описывать топлу людей как сжимаемую жидкость.

Параллельно с приближением сплошной среды, в последние годы набирает обороты кинетическая модель, основанная на дискретизации среды на небольшие частицы, взаимодействующие между собой (в простейшем случае — как твердые шарики, отталкивающиеся при столкновении). Такой подход возник в первую очередь благодаря развитию вычислительной техники, однако существенно новых результатов в чистую гидродинамику не превнёс, хотя оказался крайне полезен для задач физики плазмы, которая на микроуровне не является однородной, а содержит электроны и положительно заряженные ионы. Ну и опять же для моделирования Вселенной.

Уравнение неразрывности. Закон сохранения массы

Самый элементарный закон. Пусть у нас есть какой-то совершенно произвольный, но макроскопический объём жидкости V, ограниченный поверхностью F (см. рис.). Масса жидкости внутри него определяется интегралом:

И пусть с жидкостью внутри него не происходит ничего, кроме движения. То есть, там нет химических реакций и фазовых переходов, нет трубок с насосами или чёрных дыр. Ну и всё происходит с маленькими скоростями и для малых масс вещества, потому никакой теории относительности, искривления пространства, самогравитации жидкости (она становится существенна на звёздных масштабах). И пусть сам объём и границы еего неподвижны. Тогда единственное, что может изменить массу жидкости в нашем объёме — это её перетекание через границу объёма (для определённости — пусть масса в объёме убывает):

где вектор j — поток вещества через границу. Точкой, напомним, обозначается скалярное произведение. Поскольку границы объёма, как было сказано, неподвижны, то производную по времени можно внести под интеграл. А правую часть можно преобразовать к такому же, как слева, интегралу по объёму по теореме Гаусса-Остроградского.

В итоге, в обеих частях равенства получается интеграл по одному и тому же совершенно произвольному объёму, что позволяет приравнять подинтегральные выражения и перейти к дифференциальной форме уравнения:

Здесь (и далее) использован векторный оператор Гамильтона. Образно говоря, это условный вектор, компоненты которого — операторы дифференцирования по соответствующим координатам. С его помощью можно очень кратко обозначать разного рода операции над скалярами, векторами, тензорами высших рангов и прочей математической нечистью, основные среди которых — градиент, дивергенция и ротор. Не буду останавливаться на них детально, поскольку это отвлекает от основной темы.

Наконец, поток вещества равен массе, переносимой через единичную площадку за единицу времени:

Окончательно, закон сохранения массы (называемый также уравнением неразрывности) для сплошной среды таков:

Это выражение наиболее общее, для среды, обладающей переменной плотностью. В реальности, эксперимент свидетельствует о крайне слабой сжимаемости жидкости и практически постоянном значении плотности, что с высокой точностью позволяет применять закон сохранения массы в виде условия несжимаемости:

которое с не менее хорошей точностью работает и для газов, пока скорость течения мала по сравнению со звуковой.

Уравнение Эйлера. Закон сохранения импульса

Весь относительно громоздкий процесс колдовства преобразования интегралов, использованный выше, даёт нам не только уравнение неразрывности. Точно такие же по сути преобразования позволяют выразить законы сохранения импульса и энергии, и получить в итоге уравнения для скорости жидкости и для переноса тепла в ней. Однако пока не будем сильно торопиться, и займёмся не просто сохранением импульса, а даже сохранением импульса в идеальной несжимаемой жидкости — т.е. рассмотрим модель с полным отсутствием вязкости.

Рассуждения практически те же самые, только теперь нас интересует не масса, а полный импульс жидкости в том же самом объёме V. Он равен:

При тех же самых условиях, что и выше, импульс в объёме может меняться за счёт:

• конвективного переноса — т.е. импульс «утекает» вместе со скоростью через границу
• давления окружающих элементов жидкости
• просто за счёт внешних сил, например — от силы тяжести.

Соответствующие интегралы (порядок отвечает списку) дают такое соотношение:

Начнём их преобразовывать. Правда, для этого нужно воспользоваться тензорным анализом и правилами работы с индексами. Конкретнее, к первому и второму интегралам применяется теорема Гаусса-Остроградского в обобщённой форме (она работает не только для векторных полей). И если перейти к дифференциальной форме уравнения, то получится следующее:

Крестик в кружочке обозначает тензорное произведение, в данном случае — векторов.

В принципе, это уже уравнение Эйлера, однако его можно чуток упростить — ведь закон сохранения массы никто не отменял. Раскрыв здесь скобки в дифференциальных операторах и приведя затем подобные слагаемые, мы увидим, что три слагаемых благополучно собираются в уравнение неразрывности, и потому дают в сумме ноль. Итоговое уравнение оказывается таким:

Если перейти в систему отсчёта, связанную с движущейся жидкостью (не будем заострять внимание на том, как это делается), мы увидим, что уравнение Эйлера выражает второй закон Ньютона для единицы объёма среды.

Учёт вязкости. Уравнение Навье-Стокса

Идеальная жидкость, это, конечно, хорошо (правда, всё равно точно не решается), но во многих случаях учёт вязкости необходим. Даже в той же конвекции, в течении жидкости по трубам. Без вязкости вода вытекала бы из наших кранов с космическими скоростями, а малейшая неоднородность температуры в воде приводила бы к её крайне быстрому и бурному перемешиванию. Потому давайте учтём сопротивление жидкости самой себе.

Дополнить уравнение Эйлера можно различными (но эквивалентными, конечно же) путями. Воспользуемся базовой техникой тензорного анализа — индексной формой записи уравнения. И пока также отбросим внешние силы, чтобы не путались под руками / под ногами / перед глазами (нужное подчеркнуть). При таком раскладе всё, кроме производной по времени, можно собрать в виде дивергенции одного такого тензора:

По смыслу, это плотность потока импульса в жидкости. К нему и нужно добавить вязкие силы в виде ещё одного тензорного слагаемого. Поскольку они явно приводят к потере энергии (и импульса), то они должны вычитаться:

Идя обратно в уравнение с таким тензором, мы получим обобщённое уравнение движения вязкой жидкости:

Оно допускает любой закон для вязкости.

Принято считать очевидным, что сопротивление зависит от скорости движения. Вязкость же, как перенос импульса между участками жидкости с различными скоростями, зависит от градиента скорости (но не от самой скорости — тому мешает принцип относительности). Если ограничиться разложением этой зависимости до линейных слагаемых, получится вот такой жутковатый объект:

в котором величина перед производной содержит 81 коэффициент. Однако, используя ряд совершенно разумных предположений об однородности и изотропности жидкости, от 81 коэффициента можно перейти всего к двум, и в общем случае для сжимаемой среды, тензор вязких напряжений равен:

где η (эта) — сдвиговая вязкость, а ζ (зета или дзета) — объёмная вязкость. Если же среда ещё и несжимаема, то достаточно одного коэффициента сдвиговой вязкости, т.к. второе слагаемое при этом уходит. Такой закон вязкости

носит название закона Навье, а полученное при его подстановке уравнение движения — это уравнение Навье-Стокса:

Точные решения

Главной проблемой гидродинамики является отсутствие точных решений её уравнений. Как бы с этим ни боролись, но получить действительно всеобщих результатов не удаётся до сих пор, и, напомню, вопрос существования и гладкости решений уравнений Навье-Стокса входит в список Проблем тысячелетия института Клэя.

Однако, несмотря на столь грустные факты, некоторые результаты есть. Здесь будут представлены далеко не все, а лишь самые простые случаи.

Потенциальные течения

Особый интерес представляют течения, в которых жидкость не завихряется. Для такой ситуации можно отказаться от рассмотрения векторного поля скорости, поскольку она выражается через градиент скалярной функции — потенциала. Потенциал же удовлетворяет хорошо изученному уравнению Лапласа, решение которого полностью определяется тем, что задано на границах рассматриваемой области:

Более того, при отсутствии вязкости из уравнения Эйлера можно однозначно выразить и давление, что вовсе замечательно и приводит нас к полному решению задачи. Ах, если бы так было всегда… то гидродинамики, наверное, уже бы и не было как современной и актуальной отрасли.

Дополнительно можно упростить задачу предположением, что течение жидкости двумерно — скажем, всё движется в плоскости (x,y), и ни одна частица не перемещается вдоль оси z. Можно показать, что в таком случае скорость может быть также заменена скалярной функцией (на этот раз — функцией тока):

которая при потенциальном течении удовлетворяет условиям Коши-Лагранжа из теории функций комплексной переменной и воспользоваться соответствующим математическим аппаратом. Полностью совпадающим с аппаратом электростатики. Теория потенциальных течений развита на высоком уровне, и в принципе хорошо описывает большой спектр задач.

Простые течения вязкой жидкости

Решения для вязкой жидкости чаще всего удаётся получить, когда из уравнения Навье-Стокса благодаря свойствам симметрии задачи выпадает нелинейное слагаемое.

Сдвиговое течение Куэтта

Самая элементарная задачка. Канал с неподвижной нижней и подвижной верхней стенкой, которая движется равномерно с некоторой скоростью. На границах жидкость прилипает к ним, так что скорость жидкости равна скорости границы. Этот результат является экспериментальным фактом, и как-то даже авторы первых экспериментов не упоминаются, просто — по совокупности экспериментов.

В такой ситуации от уравнения Навье-Стокса останется уравнение вида v» = 0, и потому профиль скорости в канале окажется линейным:

Данная задача является практически базовой для теории смазки, т.к. позволяет непосредственно определить силу, которую требуется приложить к верхней стенке для её движения с конкретной скоростью.

Течение Пуазейля

Вторая по элементарности — ламинарное течение в канале. Или в трубе. Результат оказывается один — профиль скорости является параболическим:

На основе решения Пуазейля можно определить расход жидкости через сечение канала, но, правда, только при ламинарном течении и гладких стенках. С другой стороны, для турбулентного потока и шероховатых стенок точных решений нет, а есть лишь приближённые эмпирические закономерности.

Стекание слоя жидкости по наклонной плоскости

Тут — почти как в задаче Пуазейля, только верхняя граница жидкости будет свободной. Если предположить, что по ней не бегут никакие волны, и вообще сверху нет трения, то профиль скорости будет практически нижней половинкой предыдущего рисунка. Правда, если из полученной зависимости вычислить скорость течения для средней равнинной речки, она составит около 10 км/с, и вода должна самопроизвольно отправляться в космос. Наблюдаемые в природе низкие скорости течения связаны с развитой завихренностью и турбулентностью потока, которые эффективно увеличивают вязкость воды примерно в 1 млн. раз.

В следующем посте планируется рассказать о законе сохранения энергии и соответствующих ему уравнениях переноса тепла при течении жидкости.

Динамика м кинематика потока газа в центробежных и осевых компрссорах

Основные уравнения газодинамики

Движение газового потока в проточной части лопастных компрессоров имеет сложный пространственный характер. Параметры потока (скорость, давление, плотность, температура) в различных сечениях имеют разные значения и зависят от времени. Обычно же с целью упрощения течение газа в компрессоре принимается установившимся, т. е. независимым от времени. Для вывода основных уравнений движения газа в лопастном компрессоре исходят из представления элементарной струйки газа, у которой в любом поперечном сечении изменением вышеназванных параметров можно пренебречь.

В теории лопастных компрессоров большое значение имеют уравнения постоянства массового расхода (уравнение неразрывности), количества движения и момента количества движения и уравнение энергии в абсолютном и относительном движении.

Уравнение количества движения

Фундаментальная теорема механики — импульс внешней силы равен изменению количества движения материальной системы — применительно к потоку газа в каналах лопастной машины может быть выражена уравнением,
где Р — сила, действующая со стороны потока на лопасть; G — массовый секундный расход; сть стг — средние значения скоростей в начальном и конечном сечениях.

Уравнение моментов количества движения

где М — момент, прилагаемый к массе газа G, необходимый для увеличения момента количества движения; r1, r2—соответственно радиусы начального и конечного сечений потока; с — проекции абсолютных скоростей в этих сечениях на направление окружных скоростей.

Уравнение энергии в абсолютном и относительном движении

Механический принцип рабочих процессов лопастных динамических машин, подающих непрерывную среду (жидкость или газ), одинаков: лопасти, взаимодействуя с потоком, повышают его энергию. Однако жидкость почти несжимаема, а газ сжимаем существенно, и его плотность определяется зависимостью от давления и температуры. Это обстоятельство, а также большое различие в процессах трения жидкостей и газов приводят к существенному различию физических процессов лопастных машин для сжимаемых и несжимаемых сред. В рабочих процессах лопастных компрессоров имеют место термодинамические явления.

Из уравнения следует, что энергия, сообщенная газу, расходуется на сжатие и изменение кинетической энергии газа. Член представляет собой статический напор лопастного компрессора. При течении газа в неподвижном канале, где энергия газу не сообщается и потери пренебрежимо малы.

Уравнение (4.6) называют уравнением Бернулли для установившегося абсолютного движения газа в неподвижном канале. Каналы проточной части лопастного компрессора имеют специфическую форму; некоторые из них, например межлопастные каналы рабочего колеса, вращаются.

Поэтому использование уравнений теоретической газомеханикидля расчета потоков в каналах лопастного компрессора должно проводиться с учетом их особенностей и в некоторых случаях с применением опытных коэффициентов.

Течение идеального газа в .межлопастных каналах колеса центробежного компрессора

Кинематика потока в центробежном колесе

Все лопасти рабочего колеса центробежного компрессора можно рассматривать как круговую решетку, вращающуюся с угловой скоростью. До настоящего времени газодинамика потока в таких решетках с конечным шагом лопастей недостаточно изучена. Поэтому применяются упрощенные схемы, рассматривающие течение потока в отдельных межлопастных каналах, образованных соседними лопастями.

Рассмотрим движение идеального газа во вращающемся канале произвольной формы (рис. 4.1). При постоянной ω относительное движение в межлопастных каналах можно полагать установившимся.

Абсолютная скорость с в таком потоке представляет собой векторную сумму относительной W (относительно стенок канала) и переносной (вращение вокруг оси колеса) скорости. Окружная (переносная) скорость на произвольном радиусе равна u = rw. W определяют по объемному расходу q через канал и геометрическим размерам живого сечения канала.

Результирующую абсолютную скорость с определяют построением параллелограмма скоростей. Как будет указано ниже, энергетические качества рабочего колеса определяются главным образом кинематическими соотношениями на входе 1 и выходе 2 рабочего колеса. Обычно вместо параллелограммов строят треугольники скоростей (рис. 4.2).

Составляющая абсолютной скорости сы характеризует закрутку потока при входе на лопасти. Иногда в компрессорах имеет место радиальный (без закрутки) вход потока на лопасти (рис. 4.2), треугольник скоростей для такого случая изображен штриховыми линиями. Составляющая С характеризует энергию, передаваемую газу в рабочем колесе центробежного компрессора. Радиальные составляющие абсолютной скорости определяют объемный расход на входе в колесо и выходе из него.

Механизм передачи энергии в центробежном рабочем колесе

Силовые поля потоков во вращающихся и неподвижных каналах различны.

Кроме сил, вызванных изменением величины и направления W, здесь возникает центробежная сила, вызываемая вращением в переносном движении и сила инерции, вызываемая кориолисовым ускорением. Следовательно, уравнение Бернулли в виде (4.6) в данном случае неприемлемо. К этому уравнению необходимо добавить члены, учитывающие упомянутое различие силового поля.

Равновесие сил, действующих на частицу идеального газа в направлении касательной к ее траектории s в относительном движении по принципу Даламбера, выражается уравнением,
где s — длина пути частицы; р — угол перемещения частицы в относительном движении.

Силы Кориолиса и силы, обусловленные давлением, в направлении оси п, а также сила, возникающая от поворота потока в относительном движении, направлены нормально к траектории и в условии равновесия не учитываются. Сила массы газа также не учитывается вследствие ее малости (рис. 4.1).

Степень реактивности колеса центробежного компрессора

Как следует из уравнения Эйлера, теоретический напор колеса центробежного компрессора зависит от значений u и c (при с = 0).

Для обеспечения требуемого значения действительного напора Я приходится применять различные формы лопастей рабочего колеса, обеспечивающие различные значения С2и при заданной иг. Величина игСги изменяется в широких пределах. При расчете компрессоров проектант должен знать, какую долю составляет потенциальная энергия в общей энергии, передаваемой газу в рабочем колесе. Это отношение называют степенью реактивного р и при c = 0 определяют выражением.

Отношение и угол потока на выходе из рабочего колеса в значительной степени определяют значения H и р (рис. 4.3). С увеличением С возрастает величина H.

Для предельного случая рабочее колесо создает максимальный теоретический напор в форме динамического (р = 0). Соотношение С и р зависят от 0β2.

На рис. 4.3 изображены три возможные формы лопасти при одинаковых β1, D1, D2 и С2г и соответствующее распределение энергий, поКак следует из рис. 4.3, для получения более высоких значений Ят следует выбирать повышенные значения Сги/нг- Однако это допустимо в определенных пределах. При лопастях, загнутых вперед (тип 3), основная часть приращения энергии создается в виде кинетической энергии, что приводит к большим потерям в неподвижных каналах ступени, так как каналы рабочего колеса имеют неблагоприятную форму для потока. Все это снижает КПД компрессора. Кроме того, лопасти, загнутые вперед, имеют неблагоприятные акустические качества. Рабочие колеса с такими лопастями применяются в маломощных вентиляторах. Радиальные лопасти (тип 2) применяются в нагнетателях холодильных центробежных компрессоров. Лопасти, загнутые назад (тип 1), нашли широкое применение в многоступенчатых компрессорах большой мощности.

Учет влияния конечного числа лопастей колеса центробежного компрессора

Формулы получены в предположении полной осевой симметрии потока газа в межлопастных каналах рабочего колеса, т.е. при постоянстве скоростей в выходном сечении на окружности диаметра. Это теоретически возможно при бесконечно большом количестве бесконечно тонких лопаток. При этом скорость совпадает с направлением касательной к лопасти. В этом случае суммарное приращение энергии в колесе получается простым суммированием по окружности энергий множества элементарных струек. Схема бесконечного числа лопастей была использована Эйлером и является исходным условием для приближенного определения Hт.

В действительности при конечном числе лопастей картина течения в межлопастных каналах имеет иной вид (см. рис. 4.1).

Согласно гипотезе поток в межлопастном канале можно получить путем сложения двух потоков: потока протекания и потока осевого вихря, интенсивности ω.

При сложении этих потоков (рис. 4. Г) относительная скорость на передней стороне лопасти уменьшается, a на тыльной увеличивается по сравнению со скоростью потока протекания. По уравнению Бернулли происходит изменение давления, что соответствует ранее рассмотренной картине.

В межлопастном канале на входе и выходе имеются окружные составляющие относительных скоростей.

Коэффициент р зависит от многих факторов. Несмотря на многочисленные попытки, не удалось до настоящего времени получить вполне строгое общее выражение для определения μ. Используют приближенные полузначения коэффициента р, колеблются в пределах среднестатической величины (л « 0,8.

С учетом неравномерности распределения скоростей на входе и выходе колеса полная удельная энергия (работа), переданная 1 кг массы газа, которая называется теоретическим -напором Нт, определяется выражением.

Следовательно, для определения удельной энергии, передаваемой потоку рабочим колесом, необходимо знать значения моментов скоростей (циркуляции) на входе и выходе лопастей. Величину моментов определяют экспериментально.

При рассмотрении течения газа во вращающейся круговой решетке за основу принята схема плоского (двухмерного) потока, который наиболее часто встречается в центробежных компрессорах. Если в межлопастных каналах рабочих колес имеет место пространственный (трехмерный) поток, то в этом случае приходится учитывать ряд дополнительных обстоятельств — вторичные течения, перетечки и др.

Одним из способов анализа пространственное™ потока является разбивка полости канала на ряд элементарных полостей, поверхностями вращения Ьимметричными оси колеса. В полученных элементарных полостях поток можно принимать плоским и использовать описанные выше методы.

Внутренний напор ступени центробежного компрессора

Внутренний напор ступени многоступенчатого компрессора Я,- определяет собой полную энергию, сообщенную каждому 1 кг массы газа в ступени компрессора,
где Hт — теоретический напор лопастного колеса; Hд.т — потери напора на дисковое трение; Hд, — потери напора от утечек через уплотнения колеса (Hд. т и Hд, отнесены к 1 кг массы газа).

Потери Hд. т возникают из-за трения в слоях газа близ поверхности дисков рабочего колеса.

Потери в центробежном компрессоре происходят в основном через переднее уплотнение лопастного колеса, в осевом компрессоре — между бандажом колеса и корпусом компрессора (при наличии такового).

Потери взаимно влияют друг на друга, поэтому их разделение весьма условно. (В осевых компрессорах рассмотренные выше потери незначительны, поэтому на практике ими пренебрегают)

В центробежных компрессорах применяют коэффициент закрутки потока.

Коэффициент зависит от числа лопаток и выходного угла лопаток колеса. Суммарный коэффициент, учитывающий относительные потери изменяется в пределах 1,2 ÷ 1,5.

Параметры профиля и плоской решетки профилей осевого компрессора

Течение газа в пространственных решетках рабочих колес и направляющих аппаратов имеет сложный характер. В теории и расчетах осевых компрессоров используются плоские решетки профилей, которые получаются сечением пространственных решеток рядом соосных цилиндрических поверхностей произвольного радиуса и разверткой полученных сечений на плоскость.

В результате получают плоскую решетку профилей, расположенных на одинаковом расстоянии друг от друга. При ориентировочном рассмотрении течения газа в плоской решетке осевого компрессора (плоский поток) радиальной составляющей скорости газа и взаимным влиянием профилей пренебрегают.

На рис. 4.4,а показана плоская решетка профилей, а на рис. 4.4,б — отдельный профиль. Средняя (скелетная) линия профиля — это кривая линия, разделяющая на равные части расстояние между выпуклой и вогнутой кромкой профиля, измеренное по нормали к этой линии. Среднюю линию можно построить вписанием окружностей в тело профиля. Хордой профиля называют линию, соединяющую крайние точки средней линии. За толщину профиля принимают расстояние между выпуклой и вогнутой кромками профиля, измеренное нормально к хорде, либо расстояние, измеренное нормально к средней линии профиля (т. е. диаметры вписанных окружностей). Кривизна профиля характеризуется углом Ф = θ1 + θ2, где углы θ1 и θ2 — углы между хордой и касательными к средней линии на входё и выходе профиля. Входная и выходная кромки профиля закругляются радиусами r1 и г2.

Все размеры, характеризующие профиль, могут быть представлены как относительные величины путем деления их на длину хорды.

Плоская решетка профилей характеризуется следующими величинами. Шаг решетки это расстояние между соседними профилями, измеренное по соответственным точкам профилей.

Относительный шаг решетки — это отношение шага решетки к длине хорды, т.е. который характеризует густоту решетки.

Ширина решетки — это размер решетки, параллельно оси вала компрессора. Геометрические углы входа и выхода лопастей решетки — это углы между касательными к средней линии профиля на входе и выходе и направлением оси решетки.

Угол установки профиля в решетке — это угол между хордой профиля и осью решетки. Кривизну профиля можно выразить через углы.

Поток газа, обтекающий решетку профилей, характеризуется входным углом β1 и выходным углом β2- Входной угол β1 — это угол между направлением относительной скорости на входе решетки и осью решетки. Выходной угол β2— это угол между направлением относительной скорости на выходе решетки и осью решетки. Разница между углами β2 и β1 называется углом закрутки потока. Угол атаки на входе решетки i—это угол между касательной к средней линии на входе профиля и относительной скоростью.

Угол отставания потока — это угол между касательной к средней линии на выходе профиля и относительной скоростью.

Силовое взаимодействие между прямолинейной решеткой профилей и потоком газа осевого компрессора. теорема жуковского

При обтекании профиля плоским потоком идеального газа со скоростью вследствие разных давлений на выпуклой и вогнутой сторонах профиля возникает подъемная сила. Подъемная сила перпендикулярна скоростии согласно теореме Жуковского для несжимаемой жидкости определяется на единицу длины профиля уравнением.

Теорема Жуковского действительна и для решетки профилей, если вместо скорости невозмущенного потока в уравнение ввести среднегеометрическую скорость.

КПД решетки

В осевых компрессорах применяются в основном диффузорные решетки, увеличивающие давление газового потока за счет понижения относительной скорости W.

Давление, развиваемое решеткой, работающей на реальном газе, отличается от давления, получаемого в ней прих идеальном газе при прочих равных условиях. Причиной этого является в основном газовое сопротивление межлопастных каналов, требующее для его преодоления определенных затрат энергии. Рассматривая идеальное и реальное течения при одинаковом расходе через решетку, т.е. при одинаковых скоростях на входе и выходе, перепад давлений в реальном потоке отличается от перепада давлений идеального потока, так как в реальном потоке часть перепада расходуется на гидравлические потери.

Кинематика течения в ступени осевого компрессора

Рассмотрим работу ступени осевого компрессора, состоящей из решеток вращающегося рабочего колеса и неподвижного направляющего аппарата (4.6,а). Сечением решеток ступени соосной цилиндрической поверхностью произвольного радиуса и разверткой получаем плоскую решетку профилей рабочего колеса и направляющего аппарата.

Считая радиальную составляющую скорости незначительной и пренебрегая ее влиянием, получаем равенство меридиональной и осевой составляющей скорости. Плоская решетка рабочего колеса движется с переносной скоростью и = const. Так как с — абсолютная скорость газа перед решеткой рабочего колеса, построив вектор переносной скорости и, получаем вектор относительной скорости с которой газ поступает на вращающуюся решетку колеса. Скорости образуют так называемый входной треугольник скоростей перед решеткой.

Так как W2 — относительная скорость газа на выходе решетки, добавив к ней вектор переносной скорости u1 получаем абсолютную скорость с2 на выходе из решетки. Скорости с2, и, W2 образуют так называемый выходной треугольник скоростей за решеткой.

На входе и выходе решетки рабочего колеса осевые составляющие скорости соответственно сг\ и сг2. В осевых компрессорах осевая скорость с обычно постоянна либо несколько уменьшается от первой к последней ступени.

На рис. 4.6,б, в показаны совместно скоростные треугольники на входе и выходе решетки рабочего колеса. Здесь же показана среднегеометрическая скорость

Поток газа поступает на решетку направляющего аппарата со скоростью С2 и покидает решетку со скоростью С3, несколько меньшей С2 из-за диффузорного эффекта.

Напор ступени осевого компрессора

Теоретический напор осевого компрессора представляет собой энергию, передаваемую лопатками рабочего колеса каждому 1 кг газа, проходящему через него.

Сообщение энергии материальной системе, в том числе газу, возможно только в процессе движения приложением внешней силы. Такой силой для потока газа в межлопастных каналах решетки является подъемная сила, вычисленная по формуле Жуковского.

Для существования такой силы должна иметь место разность давлений на передней и тыльной сторонах лопасти. Если обозначить через давление в середине канала на радиусе, то должно выполняться условие. В результате обтекания газовым потоком лопасти и образования перепада давления на передней и тыльной сторонах лопатки образуется циркуляционный поток. Суммарная циркуляция лопаток равна разности циркуляций на входе в колесо и выходе из него.

Теоретический напор можно выразить через циркуляцию скорости профиля решетки.

Основные кинематические схемы осевых компрессоров

В осевых компрессорах степень реактивности обычно лежит в пределах 0,5 ÷ 1,0. При р 1 происходит скачкообразное изменение параметров потока. Обратный переход от сверхзвуковых к дозвуковым значениям скоростей нельзя осуществить плавно. При переходе скорости звука в рабочей среде имеет место скачкообразное изменение параметров потока р, р и Т. Такой процесс называют скачком уплотнения (стоячей ударной волной). Скачок уплотнения сопровождается сильными акустическими явлениями (подобными преодолению звукового барьера самолетом).

При скачке уплотнения происходит резкое снижение КПД компрессора (подобно снижению КПД при кавитации в насосе). Снижение КПД в значительной степени вызвано увеличением сопротивления при обтекании профиля из-за интенсивного отрыва пограничного слоя при скачке уплотнения. При скачках уплотнения происходит необратимое преобразование кинетической энергии газа в теплоту, возникает свойственное только сверхзвуковым потокам волновое сопротивление.

На рис. 4.8 показана качественная картина дозвукового и сверхзвукового обтекания профиля.

Опасность возникновения скачка уплотнений в центробежных компрессорах относительно меньше.

Стационарные компрессоры рекомендуется выполнять при максимальных значениях числа Маха М 0,75 можно принять
ε’ = (1 — М2)ε,
где ε ≈ 8° — оптимальный угол раскрытия диффузора для несжимаемого газа.

Основы теории подобия. безразмерные коэффициенты

Лопастные компрессоры относятся к классу динамических машин. Явления, происходящие в потоке газа в проточной части, должны подчиняться общим законам динамического подобия. Поток газа в проточной части компрессора движется с высокими скоростями и, следовательно, с высокой степенью турбулентности (в квадратичной зоне режимов течения). В связи с этим условия динамического подобия течения могут выполняться, если обеспечить прежде всего требования геометрического и кинематического подобия.

Компрессоры обычно создаются сериями с геометрически подобной формой проточной части, и рабочие параметры их подчиняются основным законам подобия.

Основные критерии подобия лопастных компрессоров

При изучении подобия газодинамических процессов в лопастных компрессорах рассматриваются следующие безразмерные критерии:

• число Маха — М, характеризующее режим течения при скоростях, превышающих скорость звука в газовой среде, подаваемой компрессором;
• число Рейнольдса — Re, характеризующее режим течения при скоростях, меньших скорости звука;
• число Прандтля — Рг, оценивающее влияние тепломеханических характеристик газа на его движение и теплообмен);
• число Нуссельта — Nu, определяющее влияние теплообмена газа при его движении.

К этим четырем критериям следует добавить показатель адиабаты k. Однако выполнение равенства всех критериев подобия для двух геометрически подобных потоков невозможно.

Например, равенство чисел Re и М возможно лишь в случае, если рассматриваемые системы каналов не только подобны, но и равны по размерам. Для газовых потоков с разными показателями адиабаты невозможно сочетать геометрическое и кинематическое подобие во всех сходственных сечениях двух лопастных компрессоров. Поэтому применяется приближенное подобие, допускающее нарушение таких критериев подобия, которые в данном конкретном случае не являются определяющими.

В неохлаждаемых группах ступеней компрессорных машин процессы теплопередачи существенного значения не имеют, поэтому критерии Прандтля и Нуссельта в этих случаях можно не учитывать. Число Re оказывает влияние на характер течения.

В пределах значений М 0,8);

Необходимо отметить, что число Рr для газов с одинаковыми к (равной атомности) практически одинаковы.

В проточной части компрессора аналитическое определение основных технических характеристик с использованием методов газодинамики довольно сложно. Поэтому если известны характеристики проточной части какого-то компрессора или его ступени (обозначим индексом м), то при выполнении условий подобия можно определить характеристики разрабатываемого компрессора (индекс н).

Масштаб геометрического подобия (коэффициент пересчета)

При широком диапазоне изменения значений Хы и т обеспечить точное соблюдение условий подобия трудно.
В качестве критерия подобия в компрессоростроении используют также коэффициент быстроходности, об/мин.

Под коэффициентом быстроходности подразумевается частота вращения ступени эталонного компрессора (геометрически подобного проектируемому), который, работая на аналогичном газе при производительности VM = 1 м³/с, создает напор Ям = 1 м.

В многоступенчатых компрессорах значение пул меняется из-за изменения объемной производительности по ступеням.

Ступени с равным нуд имеют одинаковые характерные геометрические и кинематические соотношения проточной части и одинаковую безразмерную характеристику. Создаваемые серии компрессоров обычно имеют проточную часть с одинаковым Пуд.

Для энергетической и размерной характеристик ступеней используются безразмерные коэффициенты, которые также зависят от пуд. К ним относятся:

• коэффициент напора (давления). Это коэффициент, характеризующий соотношение между окружной скоростью u2 и действительным напором (повышением давления), не совсем точен, так как не учитывает изменения гидравлического КПД в подобных ступенях различных геометрических размеров. Его используют для приближенных расчетов;
• коэффициент расхода (производительности)
• коэффициент полезной мощности

Коэффициенты определяют пропускную способность, энергоемкость и размеры сечений проточной части серии подобных ступеней и используются для построения безразмерной характеристики для серий подобных машин.

Значения коэффициента ср изменяются в пределах:

• для центробежных компрессоров φ = 0,03 ÷ 0,15;
• для диагональных компрессоров φ = 0,1 ÷ 0,2.

Приняв соответствующие значения φ и имея заданные параметры V, Н и n, можно определить ориентировочно габаритный размер рабочего колеса и требуемое значение u2. По выбранным значениям входной скорости в рабочее колесо (обычно с = 20 ÷ 100 м/с) и коэффициенту φ можно оценить диаметр D0 входной воронки рабочего колеса.

Таким образом, n, φ и ψ служат исходными величинами для определения размеров элементов проточной части центробежного компрессора на заданные параметры.

Уравнение количества движения газа. Закон распределения давления в заснарядном объеме.

Для определения закономерностей распределения давления в заснарядном объёме необходимо использовать второе уравнение газодинамики – уравнение количества движения потока газа:

Место для формулы.

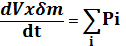
Где Pi – сумма сил, действующая на элементарную массу газа дельта м толщиной дельта х.

Уравнение известно как уравнение Бернулли, оно позволяет найти закон распределения давления в заснарядном объёме, при допущении, что изменение скорости газа между дном снаряда и дном канала ствола подчиняется линейному закону.

Дата добавления: 2015-07-06 ; просмотров: 851 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ