Марковские случайные процессы. Уравнения Колмогорова для вероятностей состояний.
Наиболее полное исследование процесса функционирования систем получается, если известны явные математические зависимости, связывающие искомые показатели с начальными условиями, параметрами и переменными исследуемой системы. Для многих современных систем, являющихся объектами моделирования, такие математические зависимости отсутствуют или малопригодны, и следует применять другое моделирование, как правило, имитационное.
Большой класс случайных процессов составляют процессы без последействия, которые в математике называют марковскими процессами в честь Андрея Андреевича Маркова — старшего (1856 — 1922), выдающегося русского математика, разработавшего основы теории таких процессов.
Случайный процесс называется марковским, если вероятность перехода системы в новое состояние зависит только от состояния системы в настоящий момент и не зависит от того, когда и каким образом система перешла в это состояние.
Практически любой случайный процесс является марковским или может быть сведен к марковскому. В последнем случае достаточно в понятие состояния включить всю предысторию смен состояний системы.
Марковские процессы делятся на два класса:
· дискретные марковские процессы (марковские цепи);
· непрерывные марковские процессы.
Дискретной марковской цепьюназывается случайный процесс, при котором смена дискретных состояний происходит в определенные моменты времени.
Непрерывным марковским процессомназывается случайный процесс, при котором смена дискретных состояний происходит в случайные моменты времени.
Рассмотрим ситуацию, когда моделируемый процесс обладает следующими особенностями.
Система 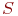
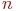
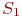
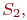
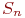
Смена состояний происходит, будем считать, мгновенно и в строго определенные моменты времени 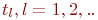
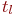
Известны вероятности перехода 

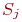
Цель моделирования: определить вероятности состояний системы после 
Обозначим эти вероятности 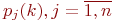

Если в системе отсутствует последействие, то есть вероятности 

Марковская цепь называется однородной, если переходные вероятности 
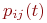
Значения 
Значения 
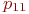
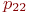
Не указываются также нулевые вероятности переходов. Например, на рис. это вероятности 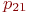
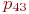
Математической моделью нахождения вероятностей состояний однородной марковской цепи является рекуррентная зависимость
где 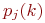
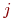

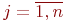
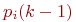
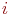

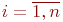
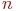

Рис.Размеченный граф состояний системы
Для неоднородной марковской цепи вероятности состояний системы находятся по формуле:
где 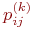

Сформулируем методику моделирования по схеме дискретных марковских процессов (марковских цепей).
1. Зафиксировать исследуемое свойство системы.
Определение свойства зависит от цели исследования. Например, если исследуется объект с целью получения характеристик надежности, то в качестве свойства следует выбрать исправность. Если исследуется загрузка системы, то — занятость. Если состояния объектов, то — поражен или непоражен.
2. Определить конечное число возможных состояний системы и убедиться в правомерности моделирования по схеме дискретных марковских процессов.
3. Составить и разметить граф состояний.
4. Определить начальное состояние.
5. По рекуррентной зависимости определить искомые вероятности.
В рамках изложенной методики моделирования исчерпывающей характеристикой поведения системы является совокупность вероятностей 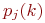
При моделировании состояния систем с непрерывными марковскими процессами мы уже не можем воспользоваться переходными вероятностями 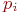

Поэтому вместо переходных вероятностей вводятся в рассмотрение плотности вероятностей переходов 
где 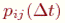


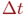
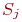
С точностью до бесконечно малых второго порядка из приведенной формулы можно представить:
Непрерывный марковский процесс называется однородным,если плотности вероятностей переходов 

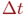
Целью моделирования,как и в случае дискретных процессов, является определение вероятностей состояний системы 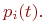
Сформулируем методику моделирования по схеме непрерывных марковских процессов.
1. Определить состояния системы и плотности вероятностей переходов 
2. Составить и разметить граф состояний.
3. Составить систему дифференциальных уравнений Колмогорова. Число уравнений в системе равно числу состояний. Каждое уравнение формируется следующим образом.
4. B левой части уравнения записывается производная вероятности 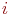
5. В правой части записывается алгебраическая сумма произведений 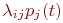
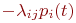
6. Определить начальные условия и решить систему дифференциальных уравнений.
Пример. Составить систему дифференциальных уравнений Колмогорова для нахождения вероятностей состояний системы, размеченный граф состояний которой представлен на рисунке.
Рис. Размеченный граф состояний
Очевидно, 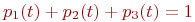
Поэтому любое из первых трех уравнений можно исключить, как линейно зависимое.
Для решения уравнений Колмогорова необходимо задать начальные условия. Для рассмотренного примера можно задать такие начальные условия: 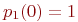
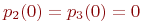
Дата добавления: 2015-04-03 ; просмотров: 7843 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Уравнения Колмогорова.
Предельные вероятности состояний
Рассмотрим математическое описание марковского процесса с дискретными состояниями и непрерывным временем* на примере случайного процесса из примера 1, граф которого изображен на рис. 1. Будем полагать, что все переходы системы из состояния в происходят под воздействием простейших потоков событий с интенсивностями ; так, переход системы из состояния в будет происходить под воздействием потока отказов первого узла, а обратный переход из состояния в — под воздействием потока «окончаний ремонтов» первого узла и т.п.
Граф состояний системы с проставленными у стрелок интенсивностями будем называть размеченным (см. рис. 1). Рассматриваемая система имеет четыре возможных состояния: .
Вероятностью i-го состояния называется вероятность того, что в момент система будет находиться в состоянии . Очевидно, что для любого момента сумма вероятностей всех состояний равна единице:
Рассмотрим систему в момент и, задав малый промежуток , найдем вероятность того, что система в момент будет находиться в состоянии . Это достигается разными способами.
1. Система в момент с вероятностью находилась в состоянии , а за время не вышла из него.
Вывести систему из этого состояния (см. граф на рис. 1) можно суммарным простейшим потоком с интенсивностью , т.е. в соответствии с формулой (7), с вероятностью, приближенно равной . А вероятность того, что система не выйдет из состояния , равна . Вероятность того, что система будет находиться в состоянии по первому способу (т.е. того, что находилась в состоянии и не выйдет из него за время ), равна по теореме умножения вероятностей:
2. Система в момент с вероятностями (или ) находилась в состоянии или и за время перешла в состояние .
Потоком интенсивностью (или — с- рис. 1) система перейдет в состояние с вероятностью, приближенно равной (или ). Вероятность того, что система будет находиться в состоянии по этому способу, равна (или ).
Применяя теорему сложения вероятностей, получим
Переходя к пределу при (приближенные равенства, связанные с применением формулы (7), перейдут в точные), получим в левой части уравнения производную (обозначим ее для простоты ):
Получили дифференциальное уравнение первого порядка, т.е. уравнение, содержащее как саму неизвестную функцию, так и ее производную первого порядка.
Рассуждая аналогично для других состояний системы , можно получить систему дифференциальных уравнений Колмогорова для вероятностей состояний:
Сформулируем правило составления уравнений Колмогорова . В левой части каждого из них стоит производная вероятности i-го состояния. В правой части — сумма произведений вероятностей всех состояний (из которых идут стрелки в данное состояние) на интенсивности соответствующих потоков событий, минус суммарная интенсивность всех потоков, выводящих систему из данного состояния, умноженная на вероятность данного (i-го состояния).
В системе (9) независимых уравнений на единицу меньше общего числа уравнений. Поэтому для решения системы необходимо добавить уравнение (8).
Особенность решения дифференциальных уравнений вообще состоит в том, что требуется задать так называемые начальные условия, т.е. в данном случае вероятности состояний системы в начальный момент . Так, например, систему уравнений (9) естественно решать при условии, что в начальный момент оба узла исправны и система находилась в состоянии , т.е. при начальных условиях .
Уравнения Колмогорова дают возможность найти все вероятности состояний как функции времени . Особый интерес представляют вероятности системы в предельном стационарном режиме , т.е. при , которые называются предельными (или финальными) вероятностями состояний.
В теории случайных процессов доказывается, что если число состояний системы конечно и из каждого из них можно (за конечное число шагов) перейти в любое другое состояние, то предельные вероятности существуют.
Предельная вероятность состояния имеет четкий смысл: она показывает среднее относительное время пребывания системы в этом состоянии . Например, если предельная вероятность состояния , т.е. , то это означает, что в среднем половину времени система находится в состоянии .
Так как предельные вероятности постоянны, то, заменяя в уравнениях Колмогорова их производные нулевыми значениями, получим систему линейных алгебраических уравнений, описывающих стационарный режим. Для системы с графом состояний, изображенном на рис. 1), такая система уравнений имеет вид:
Систему (10) можно составить непосредственно по размеченному графу состояний, если руководствоваться правилом , согласно которому слева в уравнениях стоит предельная вероятность данного состояния , умноженная на суммарную интенсивность всех потоков, ведущих из данного состояния, а справа — сумма произведений интенсивностей всех потоков, входящих в i-е состояние, на вероятности тех состояний, из которых эти потоки исходят.
Пример 2. Найти предельные вероятности для системы из примера 1, граф состояний которой приведен на рис. 1, при
Решение. Система алгебраических уравнений, описывающих стационарный режим для данной системы, имеет вид (10) или
(Здесь мы вместо одного «лишнего» уравнения системы (10) записали нормировочное условие (8)).
Решив систему (11), получим , т.е. в предельном, стационарном режиме система в среднем 40% времени будет находиться в состоянии (оба узла исправны), 20% — в состоянии (первый узел ремонтируется, второй работает), 27% — в состоянии (второй узел ремонтируется, первый работает) и 13% времени — в состоянии (оба узла ремонтируются)
Пример 3. Найти средний чистый доход от эксплуатации в стационарном режиме системы в условиях примеров 1 и 2, если известно, что в единицу времени исправная работа первого и второго узлов приносит доход соответственно в 10 и 6 ден.ед., а их ремонт требует затрат соответственно в 4 и 2 ден.ед. Оценить экономическую эффективность имеющейся возможности уменьшения вдвое среднего времени ремонта каждого из двух узлов, если при этом придется вдвое увеличить затраты на ремонт каждого узла (в единицу времени).
Решение. Из примера 2 следует, что в среднем первый узел исправно работает долю времени, равную , а второй узел — . В то же время первый узел находится в ремонте в среднем долю времени, равную , а второй узел — . Поэтому средний чистый доход в единицу времени от эксплуатации системы, т.е. разность между доходами и затратами, равен
Уменьшение вдвое среднего времени ремонта каждого из узлов в соответствии с (6) будет означать увеличение вдвое интенсивностей потока «окончаний ремонтов» каждого узла, т.е. теперь и система линейных алгебраических уравнений (10), описывающая стационарный режим системы , вместе с нормировочным условием (8) примет вид:
Решив систему, получим .
Учитывая, что , а затраты на ремонт первого и второго узла составляют теперь соответственно 8 и 4 ден.ед., вычислим средний чистый доход в единицу времени:
Так как больше (примерно на 20%), то экономическая целесообразность ускорения ремонтов узлов очевидна.
Процесс гибели и размножения
В теории массового обслуживания широкое распространение имеет специальный класс случайных процессов — так называемый процесс гибели и размножения . Название этого процесса связано с рядом биологических задач, где он является математической моделью изменения численности биологических популяций.
Граф состояний процесса гибели и размножения имеет вид, показанный на рис. 4.
Рассмотрим упорядоченное множество состояний системы . Переходы могут осуществляться из любого состояния только в состояния с соседними номерами, т.е. из состояния возможны переходы только либо в состояние , либо в состояние .
Предположим, что все потоки событий, переводящие систему по стрелкам графа, простейшие с соответствующими интенсивностями или .
По графу, представленному на рис. 4, составим и решим алгебраические уравнения для предельных вероятностей состояний (их существование вытекает из возможности перехода из каждого состояния в каждое другое и конечности числа состояний).
В соответствии с правилом составления таких уравнений (см. 13) получим: для состояния
для состояния имеем , которое с учетом (12) приводится к виду
Аналогично, записывая уравнения для предельных вероятностей других состояний, можно получить следующую систему уравнений:
к которой добавляется нормировочное условие
При анализе численности популяций считают, что состояние соответствует численности популяции, равной , и переход системы из состояния в состояние происходит при рождении одного члена популяции, а переход в состояние — при гибели одного члена популяции.
Решая систему (14), (15), можно получить
Легко заметить, что в формулах (17) для коэффициенты при есть слагаемые, стоящие после единицы в формуле (16). Числители этих коэффициентов представляют произведение всех интенсивностей, стоящих у стрелок, ведущих слева направо до данного состояния , а знаменатели — произведение всех интенсивностей, стоящих у стрелок, ведущих справа налево до состояния .
Пример 4. Процесс гибели и размножения представлен графом (рис. 5). Найти предельные вероятности состояний.
Теория массового обслуживания
Теория массового обслуживания
§1. Марковские цепи с конечным числом состояний и дискретным временем.
Пусть некоторая система S может находиться в одном из состояний конечного (или счетного) множества возможных состояний S1, S2,…, Sn, а переход из одного состояния в другое возможен только в определенные дискретные моменты времени t1, t2, t3, …, называемые шагами.
Если система переходит из одного состояния в другое случайно, то говорят, что имеет место случайный процесс с дискретным временем.
Случайный процесс называется марковским, если вероятность перехода из любого состояния Si в любое состояние Sj не зависит от того, как и когда система S попала в состояние Si (т. е. в системе S отсутствует последствие). В таком случае говорят, что функционирование системы S описывается дискретной цепью Маркова.
Переходы системы S в различные состояния удобно изображать с помощью графа состояний (рис.1).
 |
Рис. 1
Вершины графа S1, S2, S3 обозначают возможные состояния системы. Стрелка, направленная из вершины Si в вершину Sj обозначает переход Si → Sj; число, стоящее рядом со стрелкой, обозначает величину вероятности этого перехода. Стрелка, замыкающаяся на i-той вершине графа, обозначает, что система остается в состоянии Si с вероятностью, стоящей у стрелки.
Графу системы, содержащему n вершин, можно поставить в соответствие матрицу n´n, элементами которой являются вероятности переходов pij между вершинами графа. Например, граф на рис.1 описывается матрицей P:

называемой матрицей вероятностей переходов. Элементы матрицы pij удовлетворяют условиям:


Условие (1.1) — обычное свойство вероятностей, а условие (1.2) (сумма элементов любой стрелки равна 1) означает, что система S обязательно либо переходит их какого-то состояния Si в другое состояние, либо остается в состоянии Si.
Элементы матрицы 

В общем случае перехода Si → Sj за m шагов для элементов  матрицы вероятностей переходов справедлива формула:
матрицы вероятностей переходов справедлива формула:

Полагая в (1.4) l = 1 и l = m — 1 получим два эквивалентных выражения для 


Пример 1. Для графа на рис.1 найти вероятность перехода системы из состояния S1 в состояние S2 за 3 шага.
Решение. Вероятность перехода S1 → S2 за 1 шаг равна 

Аналогично 
Как видно из этой формулы, в дополнение к 



Ответ: Вероятность перехода S1 → S2 после третьего шага равна 0,183.
Пусть система S описывается матрицей вероятностей переходов Р

Если обозначить через P(m) матрицу, элементами которой являются 
где матрица Pm получается умножением матрицы P саму на себя m раз.
Исходное состояние системы характеризуется вектором состояния системы (называемым также стохастическим вектором).
где qj-вероятность того, что исходным состоянием системы является Sj состояние. Аналогично (1.1) и (1.2) справедливы соотношения
0 ≤ qi ≤1;
Обозначим через
вектор состояния системы после m шагов, где 

Пример 2. Найти вектор состояния системы, изображенный на рис.1 после двух шагов.
Решение. Исходное состояние системы характеризуется вектором =(0,7; 0; 0,3). После первого шага (m = 1) система перейдет в состояние
После второго шага система окажется в состоянии
Ответ: Состояние системы S после двух шагов характеризуется вектором (0,519; 0,17; 0,311).
При решении задач в примерах 1, 2 предполагалось, что вероятности переходов Pij остаются постоянными. Такие марковские цепи называются стационарными. В противном случае марковская цепь называется нестационарной.
§2. Марковские цепи с конечным числом состояний и непрерывным временем.
Если система S может переходить в другое состояние случайным образом в произвольный момент времени, то говорят о случайном процессе с непрерывным временем. В отсутствии последействия такой процесс называется непрерывной марковской цепью. При этом вероятности переходов Si → Sj для любых i и j в любой момент времени равны нулю (в силу непрерывности времени). По этой причине вместо вероятности перехода Pij вводится величина λij — плотность вероятности перехода из состояния Si в состояние Sj, определяемая как предел

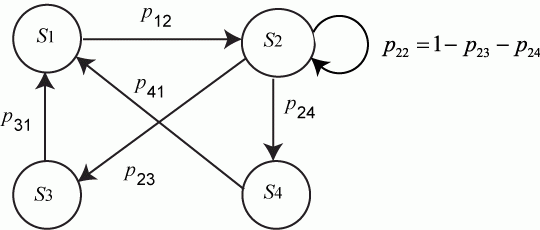
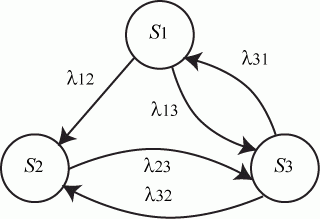
Если величины λij не зависят от t, то марковский процесс называется однородным. Если за время Δt система может изменить свое состояние не более чем один раз, то говорят, что случайный процесс является ординарным. Величину λij называют интенсивностью перехода системы из Si в Sj. На графе состояний системы численные значения λij ставят рядом со стрелками, показывающими переходы в вершины графа (рис. 2).

Рис. 2
Зная интенсивности переходов можно найти величины p1(t), p2(t),…, pn(t) — вероятности нахождения системы S в состояниях S1, S2,…, Sn соответственно. При этом выполняется условие

Распределение вероятностей состояний системы, которое можно характеризовать вектором 

Состояния Si и Sj называются сообщающимися, если возможны переходы Si ↔ Sj (на рис. 2 сообщающимися являются состояния S1 и S2, а S1, S3 и S2, S3 такими не являются).
Состояние Si называется существенным, если всякое Sj, достижимое из Si, является сообщающимся с Si. Состояние Si называется несущественным, если оно не является существенным (на рис. 2 существенными являются состояния S1 и S2).
Если существуют предельные вероятности состояний системы


не зависящие от начального состояния системы, то говорят, что при t → ∞ в системе устанавливается стационарный режим.
Система, в которой существуют предельные (финальные) вероятности состояний системы, называется эргодической, а протекающий в ней случайный процесс эргодическим.
Теорема 1. Если Si – несущественное состояние, то

т. е. при t → ∞ система выходит из любого несущественного состояния (для системы на рис. 2 
Теорема 2. Чтобы система с конечным числом состояний имела единственное предельное распределение вероятностей состояний, необходимо и достаточно, чтобы все ее существенные состояния сообщались между собой (система на рис.2 удовлетворяет этому условию, т. к. существенные состояния S1 и S2 сообщаются между собой).
Если случайный процесс, происходящий в системе с дискретными состояниями является непрерывной марковской цепью, то для вероятностей p1(t), p2(t),…, pn(t) можно составить систему линейных дифференциальных уравнений, называемых уравнениями Колмогорова. При составлении уравнений удобно пользоваться графом состояний системы. Рассмотрим получение уравнений Колмогорова на конкретном примере.
Пример 3. Записать уравнения Колмогорова для системы, изображенной на рис.2. Найти финальные вероятности для состояний системы.
Решение. Рассмотрим вначале вершину графа S1. Вероятность p1(t + Δt) того, что система в момент времени (t + Δt) будет находиться в состоянии S1 достигается двумя способами:
а) система в момент времени t с вероятностью p1(t) находилась в состоянии S1 и за малое время Δt не перешла в состояние S2. Из состояния S1 система может быть выведена потоком интенсивностью λ12; вероятность выхода системы из состояния S1 за время Δt при этом равна (с точностью до величин более высокого порядка малости по Δt) λ12 Δt, а вероятность невыхода из состояния S1 будет равна (1 — λ12 Δt). При этом вероятность того, что система останется в состоянии S1, согласно теореме об умножении вероятностей будет равна p1(t) (1 — λ12 Δt).
б) система в момент времени t находилась в состоянии S2 и за время Δt под воздействием потока λ21 перешла в состояние S1 с вероятностью λ21 Δt. Вероятность того, что система будет находиться в состоянии S1 равна p2(t)∙λ21Δt.
в) система в момент времени t находилась в состоянии S3 и за время Δt под воздействием потока λ31 перешла в состояние S1 с вероятностью λ31 Δt. Вероятность того, что система будет находиться в состоянии S1 равна p3(t)∙λ31Δt.
По теореме сложения вероятностей получим:
p1(t + Δt) = p1(t) (1 — λ12 Δt) + p2(t) (1 — λ21 Δt) + p3(t) (1 – λ31 Δt);
p1(t + Δt) — p1(t) = (-p1(t)·λ12 + p2(t) λ21 + p3(t) λ31) Δt
Переходя к пределу Δt → 0, получим

Аналогично, рассматривая вершины графа S2 и S3 , получим уравнения


К уравнениям (2.5) – (2.7) следует добавить уравнение (2.2), имеющее в данном случае вид
Уравнение (2.8) выполняет роль нормировочного условия, накладываемого на вероятности pj.
Решение системы уравнений (2.5) – (2.8) в зависимости от времени можно найти либо аналитически, либо численно с учетом начальных условий. Мы найдем лишь финальные вероятности pj, которые по определению при t → ∞ не зависят от времени. При этом в (2.5) – (2.7) dpi/dt = 0 (j = 1, 2, 3). Получившиеся при этом три алгебраических уравнения являются однородными, поэтому одно из них можно отбросить. Отбросим, например, уравнение, получающееся из (2.6), а вместо него запишем уравнение (2.8). В результате система уравнений для финальных вероятностей примет вид
Из последнего уравнения следует, что p3 = 0. Решая оставшиеся уравнения, получим p1= 2/3, p2 = 1/3.
Ответ: вектор состояния системы в стационарном режиме равен
С учетом рассмотренного примера сформулируем общее правило составления уравнений Колмогорова:
В левой части каждого из них стоит производная вероятности какого-то (j-го) состояния. В правой части — сумма произведений вероятностей всех состояний, из которых идут стрелки в данное состояние, на интенсивности соответствующих потоков, минус суммарная интенсивность всех потоков, выводящих систему из данного (j-го) состояния, умноженная на вероятность данного (j-го) состояния.
§3. Процессы рождения и гибели.
Так называется широкий класс случайных процессов, происходящих в системе, размеченный граф состояний которой изображен на рис. 3.


λ0 λ1 λ2 λg-2 λ g-1

Здесь величины λ0, λ1,…, λg-1 — интенсивности переходов системы из состояния в состояние слева направо, можно интерпретировать как интенсивности рождения (возникновения заявок) в системе. Аналогично, величины μ0, μ 1,…, μ g-1 — интенсивности переходов системы из состояния в состояние справа налево, можно интерпретировать как интенсивности гибели (выполнения заявок) в системе.
Поскольку все состояния являются сообщающимися и существенными, существует (в силу теоремы 2) предельное (финальное) распределение вероятностей состояний. Получим формулы для финальных вероятностей состояний системы.
В стационарных условиях для каждого состояния поток, втекающий в данное состояние должен равняться потоку, вытекающему из данного состояния. Таким образом, имеем:
для состояния S0 :
p0∙λ0Δt = p1∙μ 0Δt;
для состояния S1:
р1·(λ1 + μ 0)Δt = p0∙λ0Δt + p2∙μ1·Δt;
Последнее уравнение с учётом предыдущего можно привести к виду λ1 p1 = μ1p2. Аналогично можно получить уравнения для остальных состояний системы. В результате получится система уравнений:

Последнее уравнение в (3.1) является очевидным условием (2.2). Решение системы уравнений (3.1) имеет вид:






§4. Основные понятия и классификация систем массового обслуживания. Простейший поток заявок.
Заявкой (или требованием) называется спрос на удовлетворение какой-либо потребности (далее потребности предполагаются однотипными). Выполнение заявки называется обслуживанием заявки.
Системой массового обслуживания (СМО) называется любая система для выполнения заявок, поступающих в неё в случайные моменты времени.
Поступление заявки в СМО называется событием. Последовательность событий, заключающихся в поступлении заявок в СМО, называется входящим потоком заявок. Последовательность событий, заключающихся в выполнении заявок в СМО, называется выходящим потоком заявок.
Поток заявок называется простейшим, если он удовлетворяет следующим условиям:
1)отсутствие последействия, т. е. заявки поступают независимо друг от друга;
2)стационарность, т. е. вероятность поступления данного числа заявок на любом временнóм отрезке [t1, t2] зависит лишь от величины этого отрезка и не зависит от значения t1, что позволяет говорить о среднем числе заявок за единицу времени, l, называемом интенсивностью потока заявок;
3)ординарность, т. е. в любой момент времени в СМО поступает лишь одна заявка, а поступление одновременно двух и более заявок пренебрежимо мало.
Для простейшего потока вероятность pi(t) поступления в СМО ровно i заявок за время t вычисляется по формуле

т. е. вероятности распределены по закону Пуассона с параметром lt. По этой причине простейший поток называется также пуассоновским потоком.
Функция распределения F(t) случайного интервала времени T между двумя последовательными заявками по определению равна F(t) = P(T 0),
а математическое ожидание, дисперсия и среднее квадратическое отклонение случайной величины T равны соответственно



Пример 4. В справочное бюро обращается в среднем 2 человека за 10 минут. Найти вероятность того, что за 30 минут за справкой обратится:
а) 4 человека, б) не менее 3-х человек.
Решение. Интенсивность потока заявок равна λ = 2/10 мин = 0,2[мин-1]. Для решения используем формулу (4.1), где полагаем t = T = 30 минут; для пункта (а) i = 4, для пункта (б) i = 3, 4, 5,… .
а) 
б) при решении этого пункта целесообразно использовать противоположную вероятность:

Пример 5. В приборе имеются два блока, работающих независимо друг от друга. Время безотказной работы определяется показательным законом. Среднее время безотказной работы 1-го блока – t1 = 2 года, 2-го – t2 = 1 год. Найти вероятность того, что за 1,5 года: а) не откажет ни один из блоков; б) откажет только 2-й блок; в) откажут оба блока.
Решение: В качестве события выступает неисправность какого-то блока. Вероятность p(i) (t) исправности i-го блока в течение времени t определяется формулой (4.2), т. е.
где λ1 = 1/t1 = 0,5[год-1], λ2 = 1/t2 = 1[год-1].
Вероятности исправности блоков по истечении времени t = T = 1,5 года будут равны соответственно
Вероятность того, что за время T i-й блок выйдет из строя, является противоположной вероятностью
Обозначим через А, В, С события, фигурирующие в пунктах (а), (б), (в) соответственно и учитывая, что блоки работают независимо друг от друга, найдём:
а)
б)
в)
Каналом обслуживания называется устройство в СМО, обслуживающее заявку. СМО, содержащее один канал обслуживания, называется одноканальной, а содержащее более одного канала обслуживания – многоканальной (например, 3 кассы на вокзале).
Если заявка, поступающая в СМО, может получить отказ в обслуживании (в силу занятости всех каналов обслуживания) и в случае отказа вынуждена покинуть СМО, то такая СМО называется СМО с отказами (примером такой СМО может служить АТС).
Если в случае отказа в обслуживании заявки могут вставать в очередь, то такие СМО называются СМО с очередью (или с ожиданием). При этом различают СМО с ограниченной и неограниченной очередью. Примером первых СМО может служить мойка для автомашин с маленькой стоянкой для ожидающих машин, а примером вторых СМО может служить билетная касса или метрополитен.
Возможны также СМО смешанного типа, когда, например, заявка может вставать в очередь, если она не очень велика, и может находиться в очереди ограниченное время и уйти из СМО не обслуженной.
Различают СМО открытого и замкнутого типа. В СМО открытого типа поток заявок не зависит от СМО (билетные кассы, очередь в булочной). В СМО замкнутого типа обслуживается ограниченный круг клиентов, а число заявок может существенно зависеть от состояния СМО (например, бригада слесарей – наладчиков, обслуживающих станки на заводе).
СМО могут также различаться по дисциплине обслуживания: обслуживаются ли заявки в порядке поступления, случайным образом или вне очереди (с приоритетом).
СМО описываются некоторыми параметрами, которые характеризуют эффективность работы системы.
λ – интенсивность поступления в СМО заявок;
μ– интенсивность обслуживания заявок;
ротк — вероятность отказа в обслуживании поступившей в СМО заявки;
Q ≡ pобс — вероятность обслуживания поступившей в СМО заявки (относительная пропускная способность СМО); при этом
А – среднее число заявок, обслуживаемых в СМО в единицу времени (абсолютная пропускная способность СМО)
Lсмо — среднее число заявок, находящихся в СМО;



где рk- вероятность системы находиться в Sk состоянии;

tож — среднее время ожидания (обслуживания) заявки в очереди,
v = 1/tож — интенсивность потока ухода заявок из очереди.
Lоч— среднее число заявок в очереди (если очередь есть); определяется как математическое ожидание случайной величины m – числа заявок, состоящих в очереди



Для открытых СМО справедливы соотношения


называемые формулами Литтла и применимые только для стационарных потоков заявок и обслуживания.
Рассмотрим некоторые конкретные типы СМО. При этом будет предполагаться, что плотность распределения промежутка времени между двумя последовательными событиями в СМО имеет показательное распределение (4.3), а все потоки являются простейшими.
§ 5. Одноканальная СМО с отказами.
Размеченный граф состояний одноканальной СМО представлен на рис.4.
 |
Здесь λ и μ – интенсивность потока заявок и выполнения заявок соответственно. Состояние системы S0 обозначает, что канал свободен, а S1 — что канал занят обслуживанием заявки.
Система дифференциальных уравнений Колмогорова для такой СМО имеет вид (см. пример 3)
где p0(t) и p1(t) — вероятности нахождения СМО в состояниях S0 и S1 соответственно. Уравнения для финальных вероятностей p0 и p1 получим, приравнивая нулю производные в первых двух уравнениях системы. В результате получим:


Вероятность p0 по своему смыслу есть вероятность обслуживания заявки pобс, т. к. канал является свободным, а вероятность р1 по своему смыслу является вероятностью отказа в обслуживании поступающей в СМО заявки ротк, т. к. канал занят обслуживанием предыдущей заявки. Остальные характеристики СМО найдём, рассмотрев конкретный пример.
Пример 6. Секретарю директора завода поступает в среднем 1,2 телефонных вызовов в минуту. Средняя продолжительность разговора составляет 2 минуты. Найти основные характеристики СМО и оценить эффективность её работы.
Решение: По условию λ = 1,2 (мин)-1, μ = 2(мин)-1, откуда ρ = λ/μ = 0,6. По формулам (5.1) и (5.2) находим робс и ротк:


Таким образом, обслуживается лишь 62,5% звонков, что нельзя считать удовлетворительным. Абсолютная пропускная способность СМО
т. е. в среднем обслуживается 0,75 звонка в минуту.
§ 6. Многоканальная СМО с отказами.
Пусть СМО содержит n каналов, интенсивность входящего потока заявок равна λ, а интенсивность обслуживания заявки каждым каналом равна μ. Размеченный граф состояний системы изображён на рис. 5.

Рис. 5
Состояние S0 означает, что все каналы свободны, состояние  означает, что обслуживанием заявок заняты k каналов. Переход из одного состояния в другое соседнее правое происходит скачкообразно под воздействием входящего потока заявок интенсивностью λ независимо от числа работающих каналов (верхние стрелки). Для перехода системы из одного состояния в соседнее левое неважно, какой именно канал освободится. Величина kμ характеризует интенсивность обслуживания заявок при работе в СМО k каналов (нижние стрелки).
означает, что обслуживанием заявок заняты k каналов. Переход из одного состояния в другое соседнее правое происходит скачкообразно под воздействием входящего потока заявок интенсивностью λ независимо от числа работающих каналов (верхние стрелки). Для перехода системы из одного состояния в соседнее левое неважно, какой именно канал освободится. Величина kμ характеризует интенсивность обслуживания заявок при работе в СМО k каналов (нижние стрелки).
Сравнивая графы на рис. 3 и на рис. 5 легко увидеть, что многоканальная СМО с отказами является частным случаем системы рождения и гибели, если в последней принять g = n и

При этом для нахождения финальных вероятностей можно воспользоваться формулами (3.2) и (3.3). С учётом (6.1) получим из них:



Формулы (6.2) и (6.3) называются формулами Эрланга – основателя теории массового обслуживания.
Вероятность отказа в обслуживании заявки ротк равна вероятности того, что все каналы заняты, т. е. система находится в состоянии Sn. Таким образом,

Относительную пропускную способность СМО найдём из (4.5) и (6.4):

Абсолютную пропускную способность найдём из (4.6) и (6.5):

Среднее число занятых обслуживанием каналов можно найти по формуле (4.7), однако сделаем это проще. Так как каждый занятый канал в единицу времени обслуживает в среднем μ заявок, то 


Пример 7. Найти оптимальное число телефонных номеров на предприятии, если заявки на переговоры поступают с интенсивностью 1,2 заявки в минуту, а средняя продолжительность разговора по телефону составляет 
Решение. Имеем: λ = 1,2 мин-1, μ = 1/t = 0,5 мин-1, ρ = λ/μ = 2,4. 
http://mathhelpplanet.com/static.php?p=uravneniya-kolmogorova
http://pandia.ru/text/78/171/24200.php
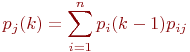
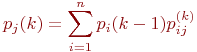
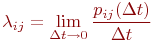
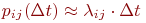
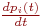
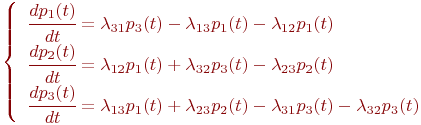































 означает, что обслуживанием заявок заняты k каналов. Переход из одного состояния в другое соседнее правое происходит скачкообразно под воздействием входящего потока заявок интенсивностью λ независимо от числа работающих каналов (верхние стрелки). Для перехода системы из одного состояния в соседнее левое неважно, какой именно канал освободится. Величина kμ характеризует интенсивность обслуживания заявок при работе в СМО k каналов (нижние стрелки).
означает, что обслуживанием заявок заняты k каналов. Переход из одного состояния в другое соседнее правое происходит скачкообразно под воздействием входящего потока заявок интенсивностью λ независимо от числа работающих каналов (верхние стрелки). Для перехода системы из одного состояния в соседнее левое неважно, какой именно канал освободится. Величина kμ характеризует интенсивность обслуживания заявок при работе в СМО k каналов (нижние стрелки).