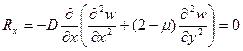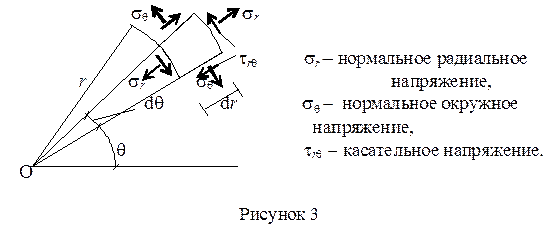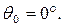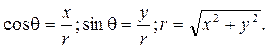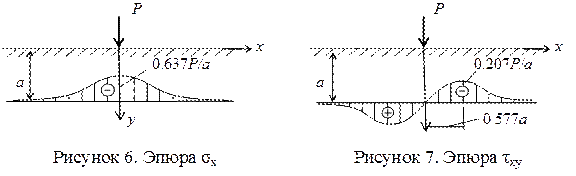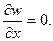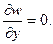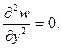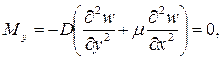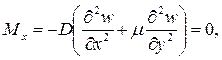Плоская задача теории упругости в полярных координатах
При решении плоской задачи в полярных координатах ряд инженерных задач удается решить путем непосредственного интегрирования исходных дифференциальных уравнений. Ориентация и обозначение напряжений в полярной системе координат показаны на рисунке 3.
Основные уравнения плоской задачи теории упругости в полярных координатах имеют вид:
(8)
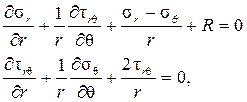
уравнение совместности деформаций в напряжениях:
(9)
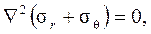
где Ñ 2 — гармонический оператор Лапласа в полярных координатах:
, (10)
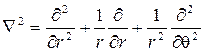
соотношения Эри и бигармоническое уравнение:
(11)
(12)
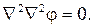
Несмотря на более громоздкий вид уравнений плоской задачи в полярных координатах для ряда инженерных задач удается найти решение в замкнутом виде.
Одной из таких задач является задача о простом радиальном напряженном состоянии, когда при интегрировании уравнений (8) и (9) получают следующее напряженное состояние:
; 
. (13)
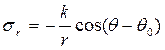
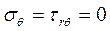
Этому состоянию соответствует задача о клине, нагруженном силой в вершине (рисунок 4).
 |
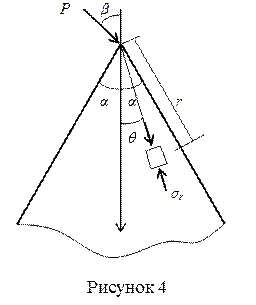Значения постоянных k и q0, можно вычислить, воспользовавшись следующими формулами:
(14)
; (15)
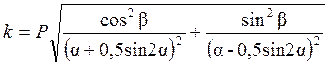
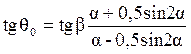
где a — угол полураствора клина и b — угол отклонения силы Р от биссектрисы угла.
Большое инженерное решение имеет частный случай — задача Фламана о действии силы на полуплоскость (рисунок 5).
 |
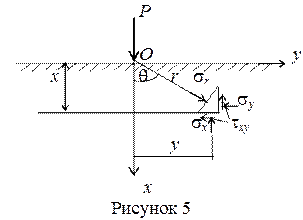В этом случае угол полураствора клина равен a = 90°, угол b = 0°.
Постоянные: k = 
Выражение для напряжений принимает вид:
Рассмотрим напряженное состояние полуплоскости на разных глубинах. Для этого удобнее перейти к декартовым координатам.
Воспользуемся выражениями для напряжений по наклонным площадкам:
(16)
(17)
(18)
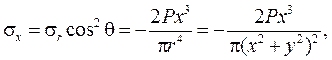
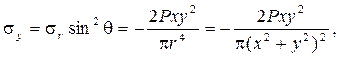
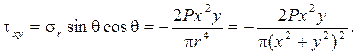
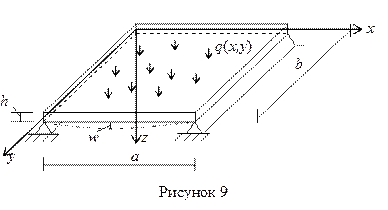
На рисунках 6 – 8 показаны эпюры напряжений в слое, отстоящем от поверхности полуплоскости на расстоянии а.
Изгиб прямоугольной пластинки
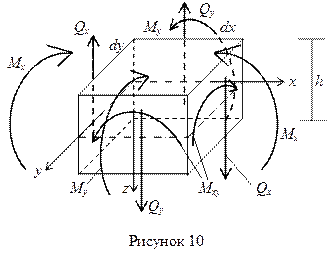
При решении задач изгиба прямоугольной пластинки (рисунок 9) функцию прогиба w(x,y) находят путем интегрирования бигармонического уравнения изгиба пластинки:
(19)
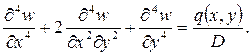
Как было указано во введении, основная и наиболее трудоемкая часть задачи расчета жесткой пластинки заключается в определении функции w(x,y) как решения бигармонического уравнения Софии Жермен — Лагранжа (19), удовлетворяющего заданной нагрузке и условиям опирания пластинки. Здесь q(x,y) –поверхностная нагрузка на пластинку; 
– цилиндрическая жесткость пластинки; h – толщина пластинки.
Внутренние усилия (рисунок 10) и напряжения в пластинке связаны с перемещениями следующими зависимостями.
(20)
(21)
(22)
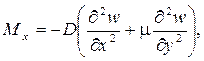
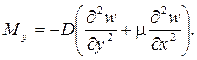
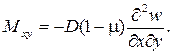
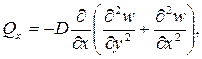
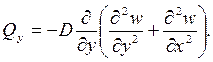
Согласно принятой в теории изгиба пластинок гипотезы Бернулли – Кирхгофа о жесткой нормали, напряжения, создающие изгибающие моменты Mx, My, определяются по формулам сопротивления материалов:
, (23)
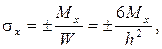
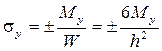
где W = 1·h 2 /6 – момент сопротивления элемента поперечного сечения пластинки единичной ширины.
Таким образом, если известна функция w(x,y), то, вычислив максимальный прогиб, можно проверить условие жесткости. Далее, определив внутренние усилия по выражениям (20) и (21), можно найти их максимальные значения и по формулам (23) вычислить наибольшие напряжения и дать оценку прочности пластинки.
Уравнение (19) имеет множество решений и для отыскания своего решения необходимо воспользоваться граничными условиями – условиями опирания пластинки.
Запись условий опирания.
В теории пластинок приняты три основных вида опирания – защемление, свободное (шарнирное) опирание и свободный неопертый край.
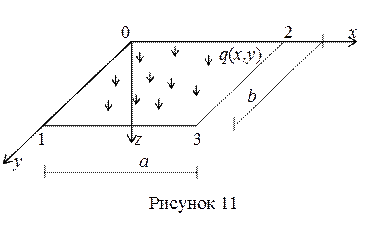
Пусть левый край пластинки 0-1 с координатами х = 0, 0 ≤ у ≤ b защемлен (рисунок 11). В этом случае граничные условия принимают вид:
2) угол поворота левой грани 
Если защемлены верхний или нижний края пластинки, условия опирания имеют аналогичные выражения:
1) прогиб w = 0, 2) угол поворота нижней (верхней) грани 
Верхний край 0 — 2 с координатами 0 ≤ x ≤ a, y = 0 шарнирно оперт. Тогда граничные условия записываются как:
Изгибающий момент на грани My = 0. Поскольку производная по х на верхней опертой грани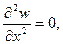 
второе условие принимает вид:
2) My = 
Если шарнирно оперты боковые грани, то условия опирания имеют вид:
1) w = 0, 2) Mx = 
Пусть нижний край 1-3 (0 ≤ x ≤ a, y = b ) неоперт. В этом случае w ≠ 0, а нулю должны быть равны усилия (реакции) на свободном неопертом крае. Т. е.
Два последних условия можно объединить в одно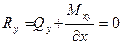 
и граничные условия примут вид:
1) 
2) 
.
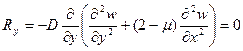
Если неоперты правый или левый край, то граничные условия запишутся как:
1) 
2) 
.