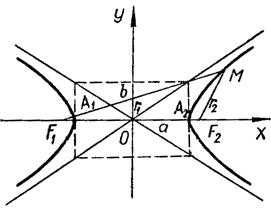
Полярное уравнение кривой второго порядка.
Пользуясь общим свойством эллипсов, гипербол и парабол, выведем общее уравнение этих кривых второго порядка в полярных координатах при некотором специальном выборе полярной системы координат.
Пусть дана произвольная из указанных линий (эллипс, ветвь гиперболы или парабола). Возьмем фокус F кривой (любой, если их два) и соответствующую ему директрису L (если рассматривается ветвь гиперболы, то берется фокус и директриса, ближайшие к этой ветви).
Введем полярную систему координат так, чтобы полюс О совпал с фокусом F, а полярная ось была направлена по оси симметрии кривой в сторону, противоположную директрисе L.
Возьмем на кривой произвольную точку М(r;j), соединим ее отрезком FM с фокусом и опустим перпендикуляр МК на директрису. Кроме того, из точки F проведем перпендикуляр FR к полярной оси до пересечения с кривой в точке R, а из точки R опустим перпендикуляр RQ на директрису (Рис. 12).
 | Обозначим FR через p и будем называть это число фокальным параметром. На основании общего свойства кривых второго порядка  По тем же соображениям: По тем же соображениям:  или или  , откуда , откуда  . . |
Подставим найденные выражения для FM и КМ в равенство 

Уравнение (3) называется уравнением кривой второго порядка в полярных координатах. При e 1 — ветвью гипиерболы, при e=1 — параболой.
Фокальный параметр Р из уравнения параболы определяется непосредственно. Для того, чтобы фокальный параметр выразить через параметры эллипса и гиперболы, следует заметить, что фокальный параметр Р является ординатой точки кривой, абсцисса которой равна абсциссе соответствующего фокуса (в выбранной при выведении канонического уравнения соответствующей кривой системе ХОY).
Подставляя вместо координат точки М(х;у) в уравнение эллипса 



Аналогично, подставляя в уравнение гиперболы координаты точки (с;р), получим:


откуда следует соотношение

Рассмотрим несколько задач на кривые второго порядка.
Задача 1.
Дано уравнение гиперболы 16х 2 -9у 2 =144. Найти длины ее осей, координаты фокусов, эксцентриситет; составить уравнения директрис и асимптот гиперболы.
Решение.
Приведем уравнение гиперболы к каноническому виду и определим как параметры гиперболы, так и расстояние с от начала координат до фокуса:


откуда а=3, b=4, 

Действительная ось 2а=6; мнимая ось 2b=8.
Уравнения директрис: 
Уравнения асимптот: 
Задача 2.
Составить уравнение эллипса, симметричного относительно координатных осей, зная, что он проходит через точки М1(2;3) и М2 
Решение.
Учитывая симметричность эллипса относительно осей координат, его каноническое уравнение будет иметь вид: 
определим параметры эллипса а и b.


получим следующую систему уравнений:

Решая ее, получим, что:

откуда а 2 =16, b 2 =12.
Следовательно, искомое уравнение эллипса будет:

Задача 3.
Найти вершину, фокус, ось и директрису параболы
Решение.
Преобразуем данное уравнение следующим образом:
Отсюда 
Обозначив х`= х-4 и у`= у-3, перейдем к новой системе координат O`x`y`, начало которой находится в точке O`(4;3), а оси O`x` и O`y` сонаправлены с осями Ох и Оу. В результате получим простейшее уравнение данной параболы

Отсюда 

xF = xO` = 4; 
то есть F 

Задача 4.
Уравнение эллипса 

Решение:
Найдем из данного уравнения параметры a, b, c, затем найдем эксцентриситет 

а 2 =4, b 2 =3, c 2 =1, 

Искомое уравнение будет иметь вид:



Задача 5.
Дано уравнение кривой в полярных координатах

Привести его к каноническому уравнению в прямоугольных координатах.
Решение.
В данном уравнении 

Из этой системы находим, что а=1, с=3, b 2 =8. Следовательно, уравнение гиперболы имеет вид:

Кривые второго порядка в полярных координатах
ВВЕДЕНИЕ
Данное руководство представляет собой методические указания к выполнению лабораторной работы, в которую входят задачи по темам: “Кривые второго порядка”, “Кривые в полярной системе координат”, “Поверхности второго порядка”.
Перед заданиями лабораторной работы приведены основные положения теории, определения, формулы, подробно рассмотрены решения типовых задач.
При выполнении лабораторной работы необходимо привести формулы, с помощью которых решается задача, сделать подробные вычисления и необходимые пояснения к решению.
ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ
Линии второго порядка
Линия (кривая) второго порядка – это линия, определяемая уравнением второй степени относительно текущих координат x и y, т.е. уравнением вида:
 | (1) |
При соответствующем выборе системы координат уравнение линии второго порядка можно привести к простейшему виду.
К линиям второго порядка относятся: эллипс, гипербола, парабола.
Эллипс. Эллипсом называется геометрическое место точек, сумма расстояний от которых до двух данных точек (фокусов) есть величина постоянная (эта постоянная больше расстояния между фокусами).
Каноническое уравнение эллипса:
 , , | (2) |
где a=ОА — большая полуось,
b=ОВ — малая полуось.
Координаты фокусов: F1(-c;0), F2(c;0), где c= 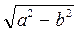
Эксцентриситетом эллипса называется отношение фокусного расстояния 2с к большой полуоси 2а: 

Директрисами эллипса называются прямые, уравнения которых 
Расстояние точки М(х,y) эллипса до фокусов (фокальные радиусы) определяются формулами:
r1= 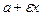 ; r2= ; r2=  . . |
В частном случае a=b фокусы F1 и F2 совпадают с центром, а каноническое уравнение имеет вид:
 , или , или  , , |
т.е. описывает окружность радиуса 
Гипербола. Гиперболой называется геометрическое место точек, разность расстояний от которых до двух данных точек (фокусов) есть величина постоянная (указанная разность берется по абсолютному значению; требуется также, чтобы она была меньше расстояния между фокусами и отлична от нуля).
Каноническое уравнение гиперболы:
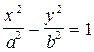 , , | (3) |
b — мнимая полуось.
Фокусы гиперболы: F1(-c;0), F2(c;0), где 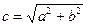
Эксцентриситетом гиперболы называется отношение 

Асимптоты гиперболы: y= 
Расстояния точки М(х;y) гиперболы до ее фокусов определяется формулами: r1= 

Прямые х= 
Гиперболы 

Гипербола с равными полуосями (a=b) называется равносторонней,ее уравнение:
 |
Парабола. Параболой называется геометрическое место точек, одинаково удаленных от данной точки (фокуса) и данной прямой (директрисы).
Уравнение параболы, симметричной относительно оси Ох и проходящей через начало координат, имеет вид:
 . . | (4) |
Уравнение директрисы 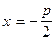

Фокальный радиус точки М(х;y) параболы выражается формулой r= 
Парабола, симметричная относительно оси Оy и проходящая через начало координат, имеет уравнение:
 | (5) |
Уравнение директрисы этой параболы: 
Фокус параболы: F (0; 
Фокальный радиус точки М(x;y) параболы: r= 
Кривые второго порядка в полярных координатах
Полярными координатами точки М на плоскости называется полярный радиус 


 |  |
| Рисунок 1 – Спираль Архимеда | Рисунок 2 – Гиперболическая спираль |
 |  |
| Рисунок 3 – Логарифмическая спираль | Рисунок 4 – Лемниската Бернулли |
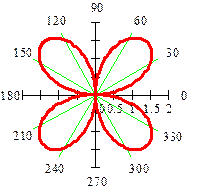 |  |
| Рисунок 5 – Четырехлепестковая роза | Рисунок 6 – Кардиоида |
 | |
| Рисунок 7 – Улитка Паскаля |
Параметрические уравнения
Параметрическими уравнениями линии на плоскости называются уравнения вида:
 | (16) |
где 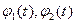
Полярная система координат. Кривые второго порядка в системе полярных координат.
| Реклама от Google |
| Доступные действия |
|
|
Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования
«Вятский государственный университет»
Факультет автоматики и вычислительной техники
Кафедра электронных вычислительных машин
Реферат студента группы ИВТ-11
(зачётная книжка №Д10-ФАВТ-2012-111)
на тему: «Полярная система координат.
Кривые второго порядка в системе полярных координат.
Решение систем линейных уравнений»
1. Полярная система координат
Полярная система координат на плоскости – это совокупность точки О, называемой полюсом, и полупрямой Ох, называемой полярной осью. Кроме того, задаётся масштабный отрезок для измерения расстояний от точек плоскости до полюса. Как правило, на полярной оси выбирается вектор 
Положение точки М в полярной системе координат определяется расстоянием r (полярным радиусом) от точки М до полюса (т.е. r = |

· в положительном направлении (против направления движения часовой стрелки), если значение угла положительное;
· в отрицательном направлении (по направлению движения часовой стрелки), если значение угла отрицательное.
Полярный радиус определён для любой точки плоскости и принимает неотрицательные значения 





С полярной системой координат Orφ можно связать прямоугольную систему координат О

Выведем формулы, связывающие прямоугольные координаты точки x, y точки М, отличной от точки О, и её полярные координаты r, φ. Получаем: 
Последние два равенства определяют полярный угол с точностью до слагаемых 







2. Уравнения кривых второго порядка в полярной системе координат
Эллипсом называется геометрическое место точек плоскости, сумма расстояний от каждой из которых до двух заданных точек F1 и F2 есть величина постоянная (2a), большая расстояния (2с) между этими двумя точками. Отношение 

Уравнение эллипса в полярной системе координат имеет вид: 

Доказательство: выберем в качестве полюса полярной системы координат левый фокус F1 эллипса, а в качестве полярной оси – луч F1F2. Тогда для произвольной точки M(r, φ) имеем r + MF2 = 2a. Выражаем расстояние между точками M(r, φ) и F2 (2с,0): 






Гиперболой называется геометрическое место двух точек плоскости, модуль разности расстояний от каждой из которых до двух заданных точек F1 и F2 есть величина постоянная (2а), меньшая расстояния (2с) между этими заданными точками. Это геометрическое определение выражает фокальное свойство гиперболы. Отношение 
Уравнение гиперболы в полярной системе координат имеет вид: 

Доказательство: выберем в качестве полюса полярной системы координат правый фокус F2 гиперболы, а в качестве полярной оси – луч с началом в точке F2, принадлежащий F1F2, но не содержащий точки F1. Тогда для произвольной M(r, φ), принадлежащей правой ветви гиперболы, имеем F1M – r =2a. Выражаем расстояние между точками М(r, φ) и F1(2c,π):


Уединяем радикал, возводим обе части уравнения в квадрат, делим на 4 и приводим подобные члены:





Параболой называется геометрическое место точек плоскости, равноудалённых от заданной точки F и заданной прямой d, не проходящей через заданную точку. Это геометрическое определение выражает фокальное свойство параболы. Эксцентриситет параболы равен 1.
Уравнение параболы в полярной системе координат имеет вид: 
Доказательство: в качестве полюса полярной системы координат выберем фокус F параболы, а в качестве полярной оси – луч с началом в точке F, перпендикулярный директрисе и не пересекающий её. Тогда для произвольной точки M(r, φ), принадлежащей параболе, MMd=r. Поскольку 

Замечание: в полярных координатах уравнения эллипса, гиперболы и параболы совпадают, но описывают разные линии, поскольку отличаются эксцентриситетами ( 


3. Решение систем линейных уравнений.
Решением системы линейных уравнений (СЛУ) называется n-ка чисел (
Если СЛУ не имеет решения, то она называется несовместной; имеет решения – совместная; 1 решение – определённая; бесконечное количество решений – неопределённая. [Из лекций]
3.1 Метод Гаусса
Метод Гаусса – метод решения СЛУ с помощью последовательного исключения переменных и приведения СЛУ к ступенчатому виду. Пусть дана СЛУ(1):
1) Будем считать (в общем случае), что 
2) Вычтем из второго уравнения первое уравнение, умноженное на 

В результате из СЛУ в уравнениях со второго по m-ное будет исключена x1. Назовём её СЛУ(2).
3) 
В результате получим: 
В результате 
1) СЛУ(1) совместна 


2) СЛУ(1) имеет 1 решение 
3) СЛУ(1) имеет 

3.2 Матричное решение СЛУ
Матрицы 







3.3 Решение методом Крамера
Для решения СЛУ(1), у которых количество неизвестных равно количеству строк, а основная матрица системы невырожденная, существует метод Крамера, который основывается на формулах 


3.4 Общее решение СЛУ
Пусть 


1. Бортаковский, Александр Сергеевич. Аналитическая геометрия в примерах и задачах.
http://megalektsii.ru/s56036t7.html
http://www.vevivi.ru/best/Polyarnaya-sistema-koordinat-Krivye-vtorogo-poryadka-v-sisteme-polyarnykh-koordinat—ref228014.html