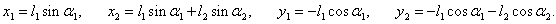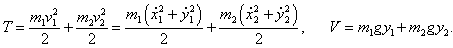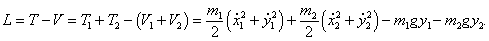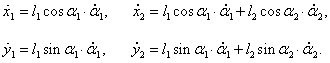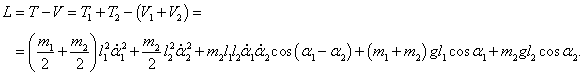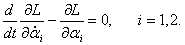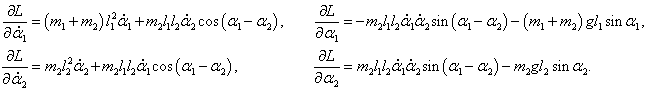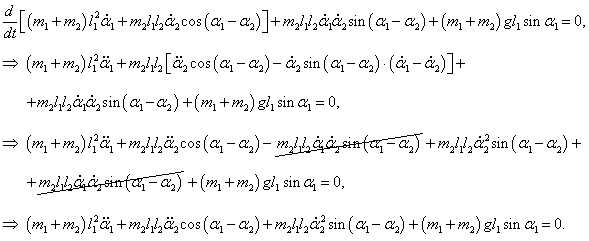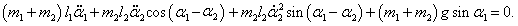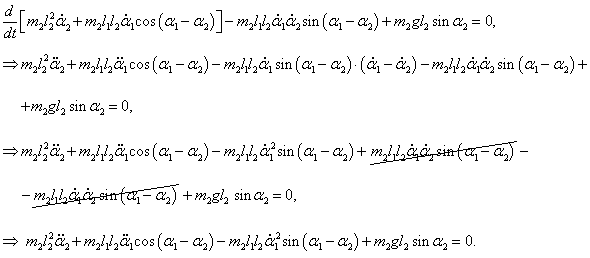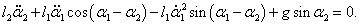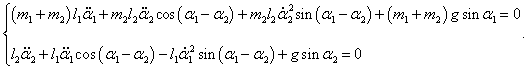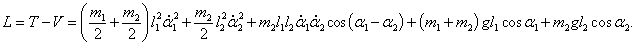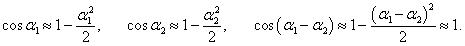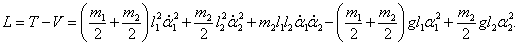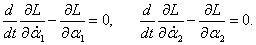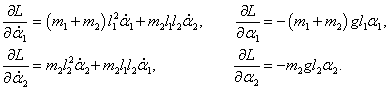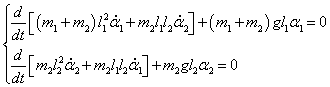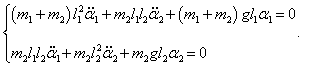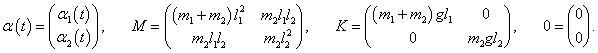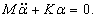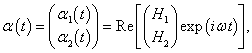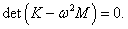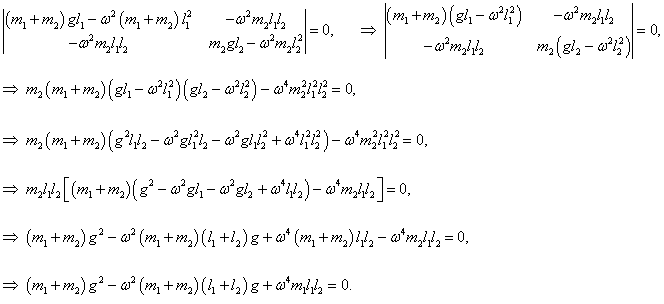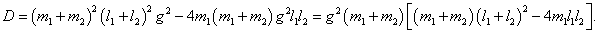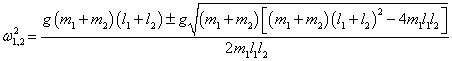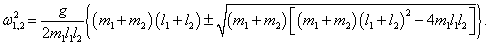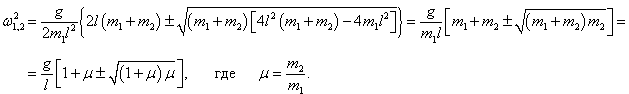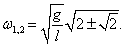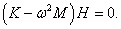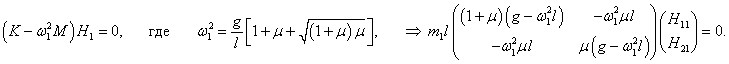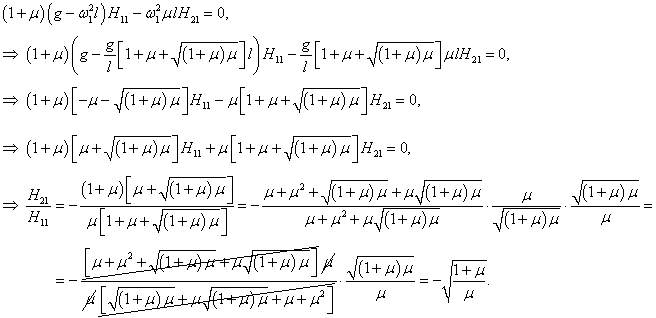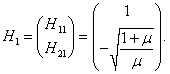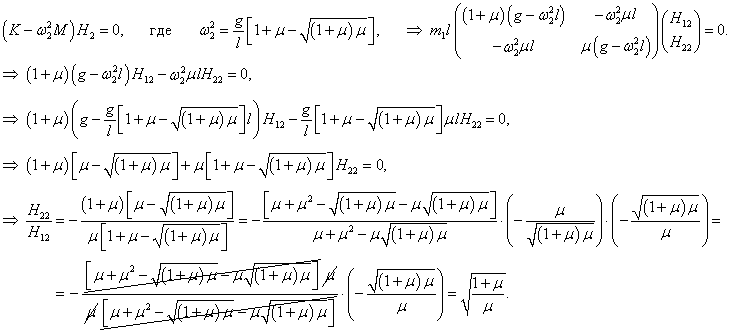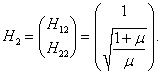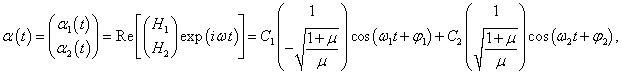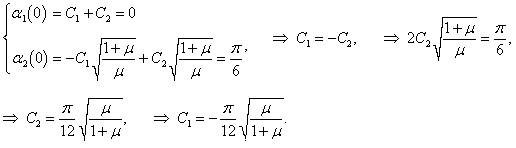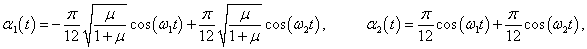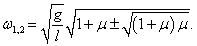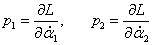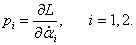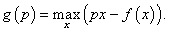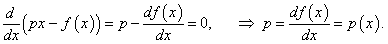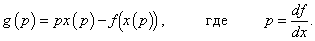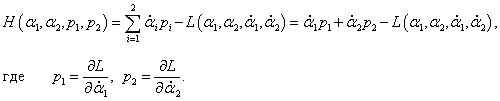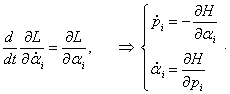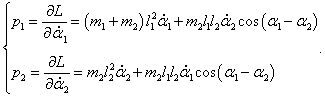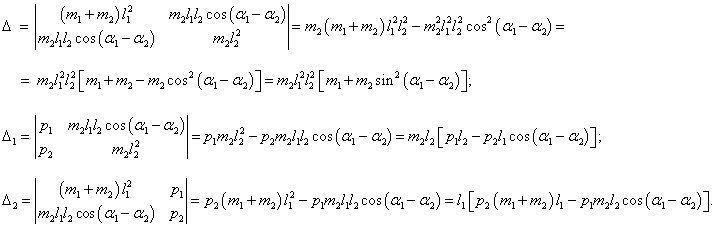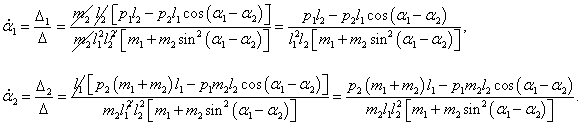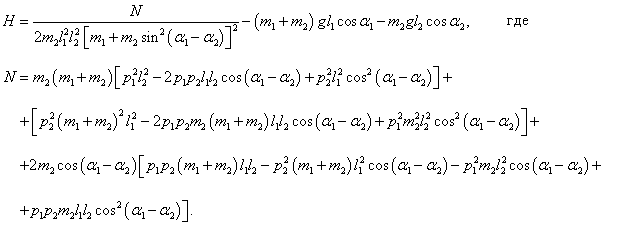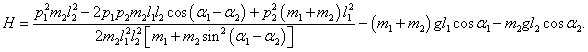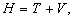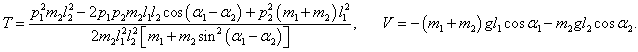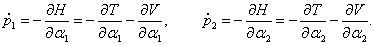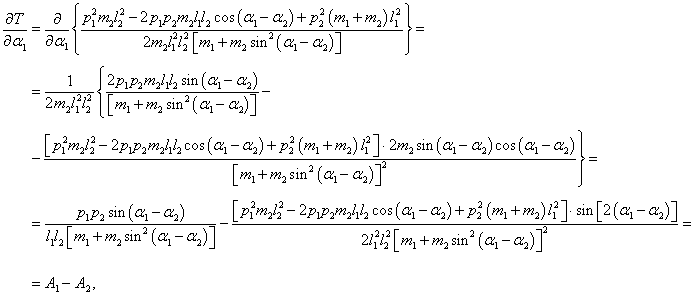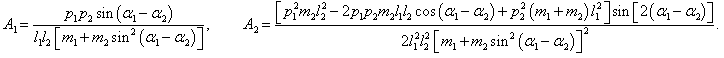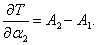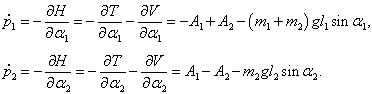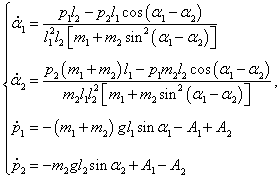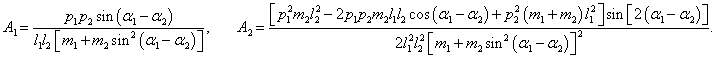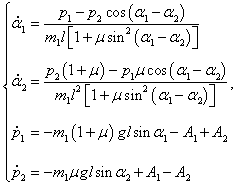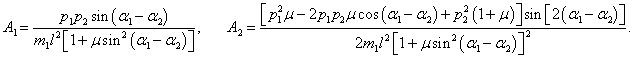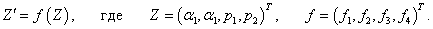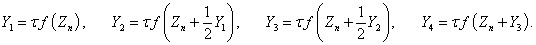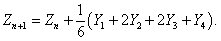Уравнение лагранжа для математического маятника

Новое в блогах

Приложения пользователя

Двойной маятник — это, несомненно, настоящее чудо природы. Поразителен скачок сложности, который наблюдается при переходе от простого одиночного маятника к двойному. Колебания простого маятника имеют регулярный характер. При малых отклонениях от равновесия такие колебания являются гармоническими и описываются функцией синус или косинус. В случае нелинейных колебаний период зависит от амплитуды, но регулярность движения сохраняется. Другими словами, в случае простого маятника приближение малых колебаний вполне отражает существенные свойства системы.

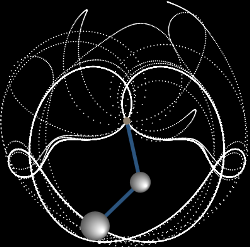
Двойной маятник «ведет себя» совершенно иначе. Уже в режиме малых колебаний у двойного маятника возникает такое новое явление как эффект биений . А при увеличении энергии характер колебаний маятников меняется принципиально − колебания становятся хаотическими . Несмотря на то, что двойной маятник можно описать системой нескольких обыкновенных дифференциальных уравнений, то есть вполне детерминированной моделью, появление хаоса выглядит очень необычно. Данная ситуация напоминает систему Лоренца , где детерминированная модель из трех уравнений также демонстрирует хаотическое поведение. Попробуйте поэкспериментировать с приведенным ниже приложением и понаблюдайте за движением двойного маятника при различных отношениях масс тел и начальных углах.

Далее мы займемся построением математической модели двойного маятника в виде системы нелинейных дифференциальных уравнений. Начнем с вывода уравнений Лагранжа .

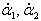
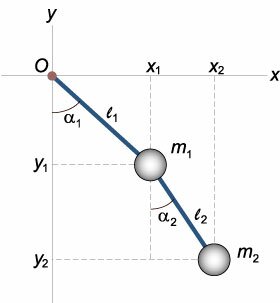
В лагранжевой механике для описания системы используются обобщенные координаты и обобщенные скорости . В нашем случае в качестве таких переменных можно взять углы отклонения маятников α₁ , α₂ и угловые скорости . Используя указанные переменные, построим лагранжиан двойного маятника и запишем дифференциальные уравнения Лагранжа.

Упрощенная модель двойного маятника показана на рисунке 1. Будем считать стержни невесомыми. Их длины равны l₁ и l₂ . Массы точечных тел (они представлены шарами конечного радиуса) составляют m₁ и m₂ . В точках подвеса трение отсутствует.

Введем систему координат O xy , начало которой совпадает с точкой подвеса. Координаты маятников определяются следующими соотношениями:

Кинетическая и потенциальная энергия маятников (соответственно T и V ) выражаются формулами

Тогда лагранжиан записывается в виде

В результате лагранжиан системы принимает такой вид:

Теперь мы можем составить уравнения Лагранжа (иногда их называют уравнениями Эйлера-Лагранжа ):

Входящие в уравнения частные производные выражаются следующими формулами:

Следовательно, первое уравнение Лагранжа записывается как

Сокращая на l₁ ≠ 0 , получаем:

Аналогично выведем второе дифференциальное уравнение:

После сокращения на m₂l₁ ≠ 0 уравнение принимает такой вид:

Таким образом, нелинейная система двух дифференциальных уравнений Лагранжа записывается как

Если считать углы α₁(t) , α₂(t) малыми, то колебания маятников вблизи нулевого положения равновесия можно описать линейной системой уравнений. Чтобы получить такую систему, вернемся назад к исходному лагранжиану системы:

Запишем этот лагранжиан в более простом виде, раскладывая его в ряд Маклорена и сохраняя линейные и квадратичные члены. Тригонометрические функции можно заменить следующими приближенными выражениями:

Здесь мы учли, что слагаемое с cos(α₁ − α₂) содержит произведение малых величин 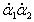и имеет второй порядок малости. Поэтому в разложении косинуса можно ограничиться линейным членом.

Подставляя это в исходный лагранжиан и учитывая, что потенциальная энергия определяется с точностью до константы, получаем квадратичный лагранжиан двойного маятника в виде:

Выведем дифференциальные уравнения Лагранжа для данного лагранжиана. Они записываются в таком виде:

Найдем частные производные:

Получаем систему двух дифференциальных уравнений Лагранжа:

Данную систему уравнений можно записать в компактной матричной форме. Введем матрицы

Тогда система дифференциальных уравнений представляется в виде

В случае одного тела такое уравнение описывает свободные незатухающие колебания с определенной частотой. В случае двойного маятника решение (как вы увидим ниже) будет содержать колебания с двумя характерными частотами, которые называются нормальными модами . Нормальные моды представляют собой действительную часть комплекснозначной векторной функции

где H₁ , H₂ − собственные векторы, ω − действительная частота. Значения нормальных частот ω_{1, 2} определяются из решения характеристического уравнения

Выведем общие формулы для циклических частот ω_{1, 2} в случае произвольных масс m₁ , m₂ и длин l₁ , l₂ :

Мы получили биквадратное уравнение для частот ω . Вычислим дискриминант:

Таким образом, квадраты нормальных частот ω_{1, 2} равны

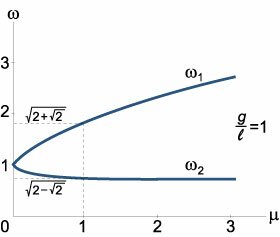
Данное выражение является несколько громоздким. Поэтому далее рассмотрим случай, когда длины стержней обоих маятников равны: l₁ = l₂ = l . Тогда нормальные частоты будут определяться более компактной формулой

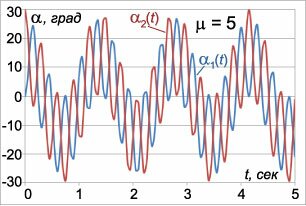
Как видно, собственные частоты ω_{1, 2} зависят лишь от отношения масс μ = m₂/m₁ . Зависимости частот ω₁ , ω₂ от параметра μ (при условии g/l = 1 ) показаны выше на рисунке 2. В частности, при равных массах m₁ = m₂ = m , т.е. при μ = 1 , собственные частоты равны

Теперь, после того как собственные частоты ω_{1, 2} известны, для описания нормальных мод нужно определить еще собственные векторы H_{1, 2} . Они находятся из решения векторно-матричного уравнения

Пусть собственный вектор H₁ = (H₁₁, H₂₁) T (верхний индекс T означает операцию транспонирования) соответствует нормальной частоте ω₁ . Тогда получаем следующее уравнение для определения H₁ :

Координаты собственного вектора H₁ удовлетворяют уравнению

Таким образом, собственный вектор H₁ равен

Аналогичным образом найдем координаты второго собственного вектора H₂ = (H₁₂, H₂₂) T :

Следовательно, собственный вектор H₂ имеет такие координаты:

Общее решение матричного уравнения записывается в виде

где постоянные C₁ , C₂ , φ₁ , φ₂ зависят от начальных положений и скоростей маятников.

Рассмотрим характер малых колебаний для некоторого конкретного набора начальных данных. Пусть, например, координаты и скорости маятников в начальный момент имеют такие значения:

В этом случае начальные фазы равны нулю: φ₁ = φ₂ = 0 . Определим постоянные C₁ и C₂ :

Тогда закон колебаний маятников выражается формулами

где циклические частоты ω_{1, 2} определяются соотношением

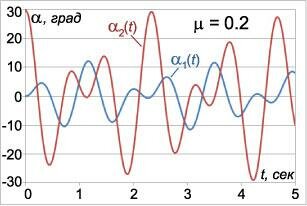
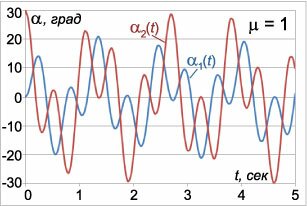
Здесь углы α₁(t) , α₂(t) выражаются в радианах, а время t в секундах. На рисунках 3-5 приведены графики малых колебаний маятников для трех значений μ : μ₁ = 0.2 , μ₂ = 1 , μ₃ = 5 , при условии l = l₁ = l₂ = 0.25 м , g = 9.8 м/c 2 . Углы отклонения маятников для удобства приведены в градусах. Из графиков видно, что в системе происходят биения , при которых энергия циклически переходит от одного маятника к другому. Когда один маятник почти останавливается, другой раскачивается с максимальной амплитудой. Через некоторое время маятники «меняются ролями» и так далее. Колебания с большей частотой ω₁ модулируются более низкочастотными колебаниями с частотой ω₂ . Это особенно хорошо заметно на рисунке 5 при большом значении μ ( μ₃ = 5 ), когда разница между частотами ω₁ и ω₂ велика.

Итак, малые колебания двойного маятника имеют периодический характер и описываются суммой двух гармоник с частотами ω₁ , ω₂ , зависящими от параметров системы. Характерным свойством малых колебаний двойного маятника является эффект биений .

Вернемся теперь снова к исходной нелинейной системе уравнений и исследуем характер колебаний с произвольной амплитудой. Такая система уравнений не решается аналитически. Поэтому мы будем рассматривать численную модель двойного маятника.

Приведенные выше уравнения Лагранжа являются дифференциальными уравнениями второго порядка. Их удобнее преобразовать в форму канонических уравнений Гамильтона . В результате вместо 2 уравнений второго порядка мы получим систему 4 дифференциальных уравнений первого порядка.

В гамильтоновой механике состояние системы определяется обобщенными координатами и обобщенными импульсами . В нашем случае в качестве обобщенных координат мы снова, как и в уравнениях Лагранжа, будем использовать углы α₁ , α₂ . Вместо обобщенных скоростей 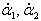(в лагранжиане) введем теперь обобщенные импульсы p₁ , p₂ , связанные со скоростями формулами

или в краткой записи:

Переход от лагранжевой к гамильтоновой форме уравнений производится с помощью преобразования Лежандра , которое определяется следующим образом.

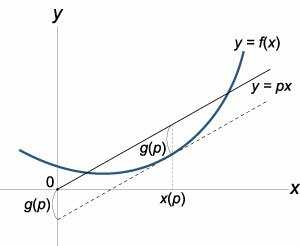
Предположим, что f ( x ) − гладкая выпуклая вниз функция (рисунок 6). Рассмотрим прямую y = px , проходящую через начало координат. Расстояние между прямой y = px и функцией y = f(x) вдоль оси O y зависит от координаты x . При определенном значении x это расстояние будет максимальным. Ясно, что оно зависит от наклона прямой, т.е. от параметра p . Таким образом мы вводим новую функцию g ( p ):

Такое преобразование функции f ( x ) в сопряженную функцию g ( p ) называется преобразованием Лежандра . Заметим, что функция g ( p ) достигает максимального значения по переменной x когда p = df/dx . Действительно,

Зная зависимость p ( x ), можно найти обратную функцию x ( p ). Тогда преобразование Лежандра будет выражаться соотношением

Преобразование Лежандра легко обобщается на случай функций нескольких переменных. В модели двойного маятника переход от функции Лагранжа к функции Гамильтона описывается преобразованием Лежандра в форме:

В этом выражении L является лагранжианом, а функция H представляет собой гамильтониан системы, который зависит от обобщенных координат α₁ , α₂ и обобщенных импульсов p₁ , p₂ .

В результате такого преобразования каждое уравнение Лагранжа переходит в систему двух канонических уравнений Гамильтона, имеющих вид:

Определим теперь конкретный вид уравнений Гамильтона для двойного маятника. Обобщенные импульсы p₁ , p₂ выражаются через частные производные лагранжиана в виде

Решим эту систему уравнений и выразим угловые скорости через обобщенные координаты и импульсы. Воспользуемся формулами Крамера и вычислим соответствующие определители:

Отсюда получаем следующие выражения для угловых скоростей:

Эти формулы представляют собой первые 2 (из 4) дифференциальных уравнений Гамильтона. С учетом данных выражений гамильтониан можно записать в следующем виде:

Последнюю формулу можно представить как

Числитель N в этом выражении является весьма громоздким. Упростим его:

Следовательно, функция Гамильтона принимает такой вид:

Здесь первое слагаемое представляет собой обобщенную кинетическую энергию T , а два других слагаемых − потенциальную энергию V , т.е. гамильтониан H определяется как

Теперь мы можем составить еще два дифференциальных уравнения Гамильтона для обобщенных импульсов:

Вычислим отдельно частные производные обобщенной кинетической энергии:

где символами A₁ и A₂ обозначены выражения

Производная кинетической энергии T по переменной α₂ будет иметь такой же вид, только с противоположным знаком:

Отсюда получаем уравнения Гамильтона в виде:

Итак, в результате громоздких преобразований мы получили то, к чему так долго стремились − систему 4 канонических уравнений Гамильтона, описывающих движение двойного маятника. Запишем их вместе в окончательном виде:

Теперь можно приступить к численному анализу уравнений.

Наиболее распространенным методом численного решения дифференциальных уравнений является метод Рунге-Кутты 4-го или 5-го порядка точности. Различные вариации этого метода используются в большинстве математических пакетов (MatLab, Maple, Mathematica, Mathcad), как правило, с автоматическим контролем точности и адаптивным временным шагом.

Для моделирования движения двойного маятника мы также воспользуемся классическим методом Рунге-Кутты 4-го порядка точности. Предварительно несколько упростим дифференциальные уравнения, полагая, что длины маятников одинаковы: l₁ = l₂ = l . Введем также параметр μ , равный отношению массы второго маятника к массе первого: μ = m₂/m₁ . Тогда система уравнений принимает следующий вид:

Данную систему можно переписать в векторной форме:

Вектор Z составлен из 4-х канонических переменных данной системы, а компоненты вектора f соответствуют правым частям дифференциальных уравнений.

Метод Рунге-Кутты предполагает на каждом шаге последовательное вычисление четырех промежуточных векторов:

Значение вектора Z_n+1 в следующем временном узле вычисляется по формуле

Суммарная ошибка данного алгоритма на конечном интервале имеет порядок O(τ 4 ) , т.е. точность вычислений возрастает в 16 раз при уменьшении временного шага τ в два раза.

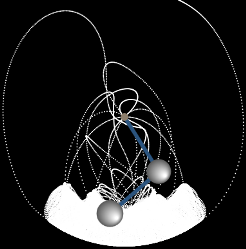
Описанная модель реализована в анимации, приведенной в начале web-страницы. Для упрощения мы положили начальные углы отклонения маятников равными: α₁ = α₂ = α . Данное приложение наглядно демонстрирует хаотическую динамику двойного маятника при различных значениях параметров μ и α . Интересно, что в некоторых режимах в системе возникают устойчивые траектории, как, например, на рисунке 7 , или компактные области притяжения, как на рисунке 8. Похоже, что двойной маятник еще не полностью изучен физиками и математиками и таит в себе много неожиданностей.

Анатолий Валетов # написал комментарий 11 февраля 2014, 21:03 Пусть в точках подвеса действуют моменты М1(t), M2(t). Масса шариков m1, m2, гравитации нет, стержни невесомые. Найти уравнения движения. Можно сначала принять моменты постоянными.

И обратная задача — даны уравнения движения, найти М1(t), M2(t)

Анатолий Валетов # ответил на комментарий Микола Борисiв 11 февраля 2014, 21:51 Т.е. обратная задача в таком случае явяется скорее всего так называемой «некорректно поставленой».
===
Представьте кульман с чертежным пантографом. Ведь каждой точке на доске соответствует строго определенное положение системы рычагов. Вот посмотрите на картинку, на мой взгляд тут есть взаимно-однозначное соответствие между динамическим уравнением происходящего на узлах и кинематическим уравнение движения карандаша.

Анатолий Валетов # ответил на комментарий Микола Борисiв 11 февраля 2014, 22:08 Не нашел точной картинки, но можно и по этой понять, если выкинуть пантограф и оставить два рычага. Двух коротких рычагов представьте что нет.

Мне хотя бы название области механики где про это почитать. Имеется ввиду манипулятор. Ну как «рука» у робота, и какие силы в узлах прикладывать чтобы она двигалась в нужном направлении.

В трех измерениях конечно будет неоднозначность, а на плоскости по-моему нет.

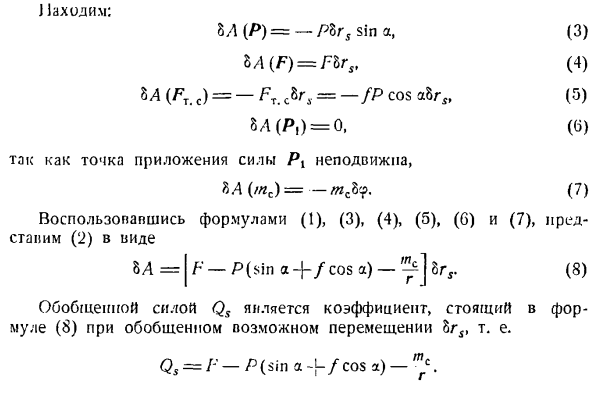
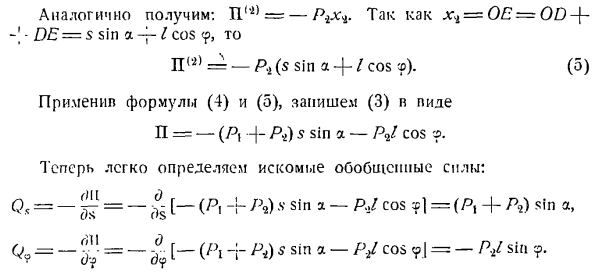
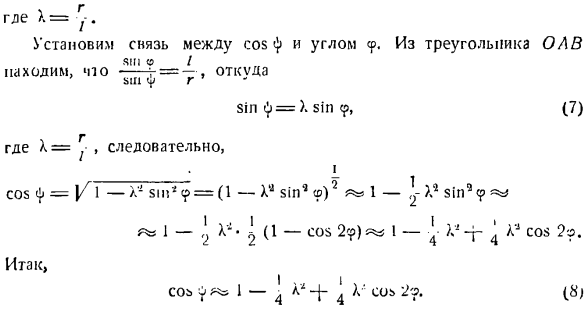
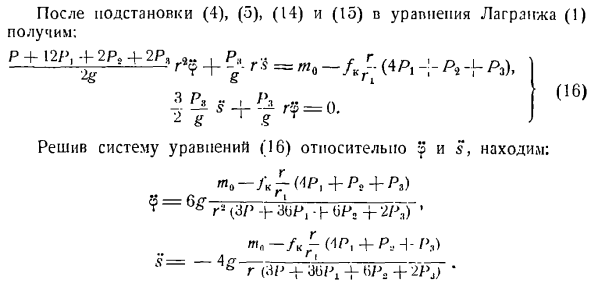
Уравнение Лангранжа второго рода

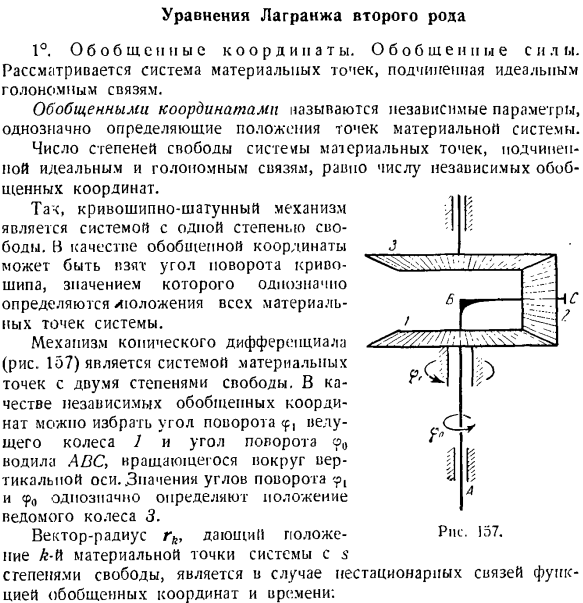
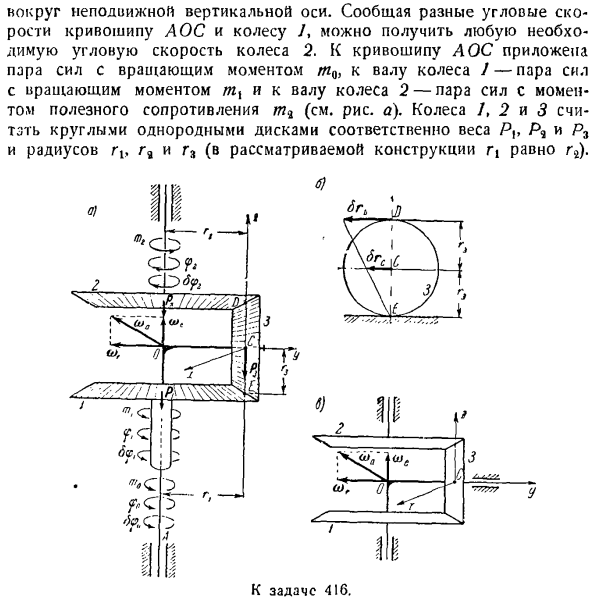
Уравнение Лагранжа типа 2 1°.Обобщенная координата. Обобщенная сила. Рассмотрим систему материальных точек, подчиненных идеальной голономной связи. Обобщенные координаты-это независимые параметры, однозначно определяющие расположение точек материальной системы. Число степеней свободы в системе масс, подчиненных идеальным и голономным отношениям, будет равно числу независимых обобщенных координат. Механизм касания

и рукоятки система с 1 степенью freedom. As обобщенные координаты можно принять за угол поворота кривошипа, величина которого однозначно определяет расположение всех важных точек системы. Механизм дифференцирования конуса (рис. 157) представляет собой систему материальных точек с 2 степенями freedom. As независимая обобщенная координата, вы можете выбрать угол поворота

Полезная сила сопротивления приложена к барабану, с моментом направленным в противоположное направление к вращению барабанчика. Людмила Фирмаль

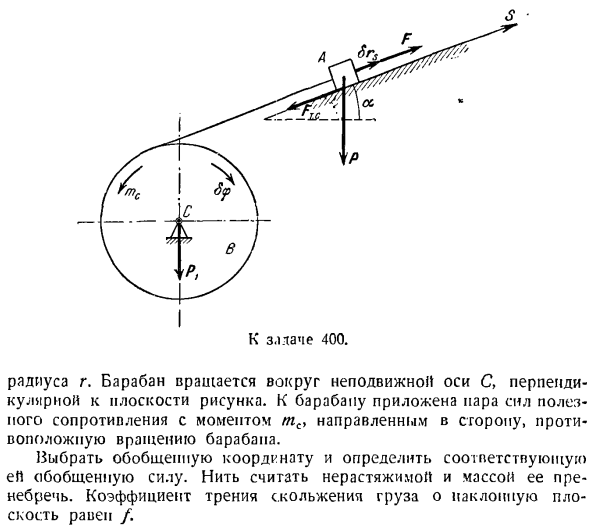
3. Радиус-вектор hl дает положение N-й материальной точки системы со степенями свободы, но в случае нестационарных соотношений он является функцией обобщенных координат и времени. И Да. О Рисунок 157. 400 к несчастью. Радиус города: барабан вращается вокруг неподвижной оси С, которая перпендикулярна плоскости рисунка. Выберите обобщенные координаты и определите соответствующие обобщенные силы. Нити считаются

расширяемыми, а их масса игнорируется. Коэффициент трения скольжения груза по наклонной плоскости равен/. Поэтому уравнения движения для целевой системы были составлены с использованием уравнений общей динамики в задаче 396 и 2 методов использования уравнений Лагрейджа в этой задаче. Сравнение двух приведенных методов показывает преимущества использования уравнения Лагранжа. Решите задачу n используя

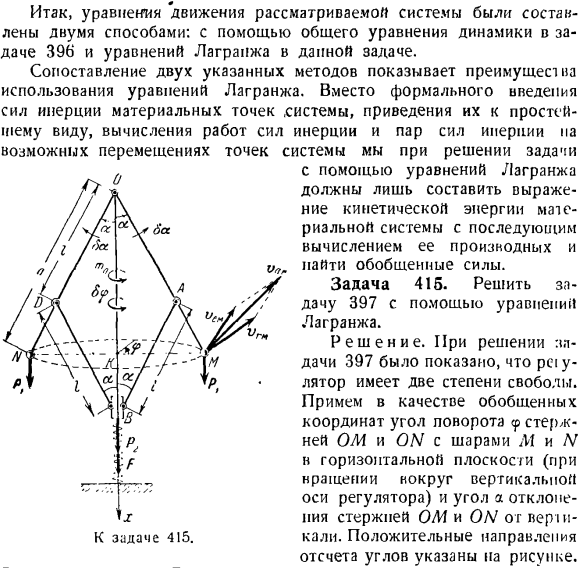
уравнение Лагранжа вместо формального введения сил инерции материальных точек системы и приведения их к простейшему виду и вычисления работы пары сил инерции относительно возможного смещения точек системы Необходимо найти обобщенную силу, составляющую лишь выражение кинетической энергии материальной системы и последующий расчет ее дифференциала.

а угол a ом и на-стержне Людмила Фирмаль

(2). Форекс-2С /(1-соз а). (2） Дадим контроллеру общее возможное смещение Sep и Sa, направленное на соответствующее увеличение угла поворота. Чтобы вычислить обобщенную силу, 8A возможно смещение, предполагая ноль, 8? ^ 0,8 а = 0. Это означает, что если угол a, образованный вертикальным стержнем OM и ON, постоянен, то регулятор получил угловое смещение 8

вычисления обобщенной силы Qa зададим регулятору возможное смещение 8a, учитывая, что возможное смещение 8

Знак минус указывает на то, что возможное движение муфты B вверх, если sin равно 8. Вычислить сумму работы заданной силы на возможном пересечении точек системы, соответствующей обобщенному возможному сдвигу 8а. В (5） (6） 8л = — 2л, sina5a-Джей-Р28лг0 + Fxbx (Коэффициент 2 в первом члене обусловлен тем, что регулятор имеет 2 шара.) Подставляя значения Lpn и Fx из формул(4)и(2), получаем: ба = — u-коэффициент абсолютной скорости для каждого из шаров M и N. каждый шар участвует в сложном движении. Угловая скорость φ-это вращение вокруг вертикальной оси регулятора, а относительное вращение вокруг горизонтальной оси O, перпендикулярной плоскости фигуры, — это угловая скорость 4.Примените теорему сложения

скоростей точек： МВС = = 4 J(10） возьмите производную по времени от координаты xn связи B относительно угла поворота d, чтобы определить проективное значение х + ^ + / ЗР (0 ′ −2–2 ВТ ДОЛГОТЫ、 Где©c-скорость центра тяжести колеса wv、 Абсолютная угловая скорость o) подвижные координатные оси x, y, g на колесах 3 a, 13x, / Lu, / Lg-осевой момент инерции,/ 3, x, / Zx-центробежный момент инерции Колесо меньше

5 для соответствующих осей. Выберите начало координат оси центроида колеса 3 C. укажите вертикальную ось g горизонтально вправо вдоль относительной оси колеса 3, а ось y, а следовательно, и ось x, перпендикулярно плоскости рисунка. При аналогичном расположении координатных осей легко заметить, что они являются главной осью инерции колеса 3(колесо 3, а также колесо/и 2, считаются однородными круговыми дисками).Результат、 = / ^. = 0, и формула для расчета кинетической энергии колеса 3 т [’л) упрощается. 7″ » =1А^ +1 (/«ш+/, v, 0j.(9） для расчета wv, shu

необходимо определить абсолютную угловую скорость колеса 3.Колесо участвует в переносных вращательных движениях угловой скорости вокруг вертикальной оси и относительных вращательных движениях вокруг оси симметрии колеса 3. давайте представим наблюдателя в провернуть операционной системы, чтобы определить, Вт. Для этого наблюдателя, этот чудик, кажется, не двигаться. Как следствие, относительную картину движения представляется глазу наблюдателя. Колеса/, 2 и 3, по-видимому, вращаются вокруг неподвижной оси(см. Рисунок C).Напишите зависимость между относительной угловой скоростью колеса и радиусом. Ин ый> Ин гл» Где ω, ω’.)) обозначает угловую скорость

колес/, 2 и 3 относительно кривошипа, вращающегося с угловой скоростью ω0.Однако 2-я дробь имеет знак минус, и если учесть пропорции вместе, то необходимо указать разные направления движения колеса/и относительную угловую скорость движения колеса/. 2.In факт、 Мл.） если бы непев жил в другом месте, то это было бы: — =- Условия r. 2 = для r1, a>(f> = = — CC) = = co0, а для coco1-ω0, o).2 =2ш0-ω, то есть =(Ю） Из первой дроби определите относительную угловую скорость»•/ » колеса 3： / «(| Гг)= т«(о).2-О)

0）、 ч’3 Возмещение (?.- ? «) •(Р） Р \ Направление масла указывается кружевом. е. Для добавления жесткого вращения вокруг пересекающихся осей применим icopevy к колесу 3: ioa — <> e + o > r(см. Рисунок? это не. Теперь нетрудно вычислить проекцию абсолютной угловой скорости G).x), колесо 3 па на оси y-z, плотно соединенное с ним. 0, Ву = — си/’, — со*). Принимая во внимание формулу (11) и отмечая ее=φ0, получим: о) = 0,о>>, =—(ти — > о ^ = Введем эти значения 0 и φ и получают производную полученного результата по времени. Мы это выясним： я£= + + + /—））»-（2 /、+ liy-r±) — ЗУ

—)7г » y3g- 2г 1 ^ г> ’Б-2г’ 4г ’ Уравнение движения дифференциала (17) принимает вид: (18） ^ [8П р?, Л = п— 2М з = мл + Ми. Используя формулу(10), вы получаете следующую формулу:$ 9 = 2?0 — подставив n в это выражение, получим искомое угловое ускорение колеса 2. .. _ _N (2L-M)+ 5(2L1- Р. Г1 Здесь Ku L1U IV D S имеет значение, описанное выше.

Решение этой задачи с помощью теоремы общей динамики сопровождается большими трудностями. Применение уравнения Лагранжа позволяет относительно легко получать дифференциальные уравнения движения, и опять же удобство применения уравнения Лагранжа при решении сложных задач динамики систем с несколькими степенями свободы.

] 1алодим： Л (/>)= — Pbr5 грех, (3） Л (Ф)= Связанные С FBR, (4） БА (м с)= — фут. с8га. = — /П, потому что АБР (5） М(П)=0.（(5), поскольку в точке действия силы P является фиксированной、 БА (МС)= — МЦБ = п — Зин Ин.(8） Потенциальная энергия весовой силы Р (4) равна пуле. N » 2> =0.(9 )） Потенциальная энергия. P13; сила упругости пружины F равна P(3)= 2.Если подставить значение выражения (2)、 =РР *(1-а°) 2. (10 )） Используя выражения (8), (9) и (10), запишите выражение (2) в следующем виде: = = P, sino -> — для R ’ 2(1-cos?2). (И） Для вычисления обобщенной силы объекта, обобщенная координата

В9 =—[РХ с COS в 09 =

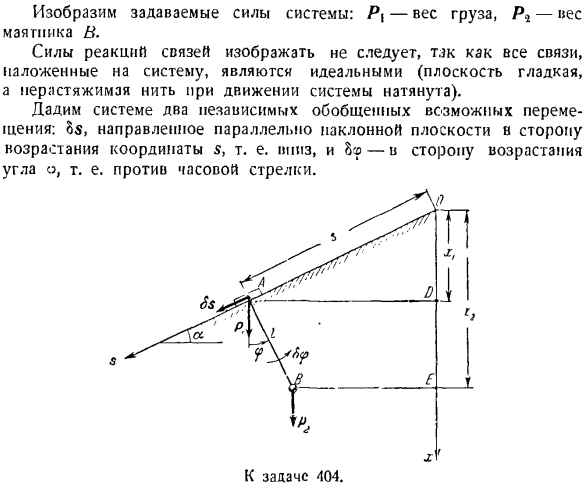
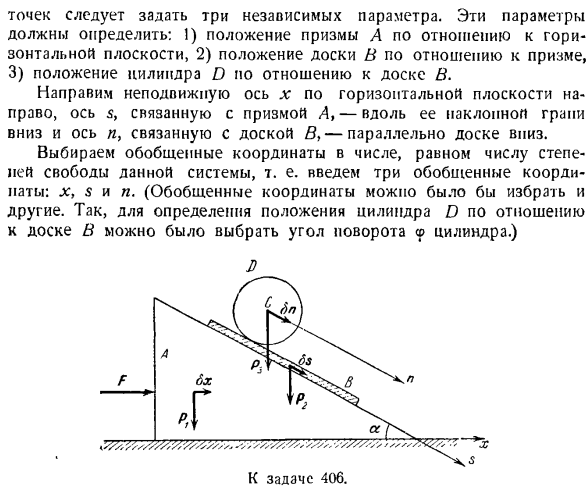
、 К М(ф)= + БГС(б） Примените Формулы(3), (4), (o) и (G)для описания (2) в виде: +(7） Обобщенная сила Q является коэффициентом пропорциональности формулы OG (7). Р Проблема 404.Груз а перемещается по гладкой наклонной плоскости угла а относительно горизонтальной плоскости. Маятник веса прикреплен к грузу A. длина строки маятника/. 」 Выберите обобщенные

ие. Поскольку для определения местоположения массы необходимо задать 2 независимых параметра, рассматриваемая система имеет 2 степени свободы. 1. один параметр определяет положение груза A на наклонной плоскости, а второй параметр определяет положение математического маятника B относительно груза A. Возьмите начало отсчета O случайным образом и направьте ось s вниз по склону. От точки O, точка вниз по оси x вертикально. Угол, под которым маятниковые нити перпендикулярны, обозначается

этой материальной системы: 5 и 9.В соответствии с этими обобщенными координатами существуют 2 обобщенные силы: Qs и Qr Показывает силу установки системы. Px-вес груза, P4-вес маятника B. Она не должна показывать силу реакции сцепления, так как все соединения, приложенные к системе, идеальны(когда система движется, плоскость становится гладкой, а вытянутые нити растягиваются). Дает системе 2 независимых обобщенных возможных перемещения. В формуле определения возможных перемещений БРК

обращает внимание читателя на то, что 1 член меньше формулы ® ). (5） Примените Формулы (4) и (5), затем напишите (3) и pide. П=-(Р,• -) — P4) 5 sin a-Р2 / cos теперь вы можете легко определить желаемую обобщенную силу. М,= — Г = — ^ [- (Р, — ’ \ РФ) с грех-Р, / Кос =(П+ а) грех、 В9 = — Ф = — у [- (РІ-Р М) ООО 《. — Пи Джей, Кос? / =- м / СР грех. Решая следующую задачу, мы можем объяснить обоснованность применения этого метода расчета обобщенных сил в случае систем с несколькими степенями свободы, в которых существуют только потенциальные заданные силы. Задача

405.Установите 3 диска в герметичный горизонтальный эластичный вал на одном конце ступени. Если центр тяжести диска находится на геометрической оси вращения, выберите обобщенные координаты и определите соответствующие обобщенные силы. Модуль упругости вала равен S. Решение. В этой системе есть 3 степени свободы. Указывает угол поворота диска, соответственно.9, cp9 и

социальная природа Формулы (1) bx-это обобщенная сила Qx. QX = R Предположим, что 8sΦ0 и bx = = op = 0 определяют обобщенную силу Qs. Это означает, что цилиндр неподвижен относительно призмы и платы относительно горизонтальной плоскости. Только плата, соединенная с цилиндром, движется вниз по боковой наклонной плоскости призмы 8s. Например, сумма работы всех сил, приведенных с возможным смещением в 8 секунд, записывается в виде 8 A = ( / > , + / > a) 8-секундный грех a. (2） Действие сил F и Px равно действию пули. Смысл действия этих сил в том, что они не движутся. Обобщенная сила Qs — это коэффициент,

представляющий собой 2s формулы (8). М,= (/Ви〜П3) грех. Переходим к расчету обобщенной силы Qn. So будем считать bnΦ0, bx = b $ = 0. Это означает, что призма неподвижна относительно призмы и горизонтальной плоскости, а поскольку душ перемещается относительно доски, его центроид C перемещается вниз вдоль оси n до 8l. Рассчитайте величину работы заданной силы на возможное перемещение Ln. БА = P38l грех. (3） Сила F, P и P. 2 задания равны нулю. Потому что точки действия этих сил не двигаются. Обобщенная сила Qn-это коэффициент, который находится в cn в уравнении(3). Дя = Пт греха я. Поэтому необходимая обобщенная сила имеет

следующий смысл: Ц = ф, Qв =(Р9-п-Р3) грех,= А. грех 2 \ обобщенное уравнение динамики в обобщенных координатах.2-й вид уравнения Лагранжа. Общая формула динамики системы масс н Х(ФК-mbwk).СРК = 0 к»■я В обобщенных координатах существует форма. [д ДТ N\, д / д ДТ от N \ ,. 。 * / д ДТ от Где Q гв. QS является обобщенной координаты, КЖ> дь QS является обобщенной скоростью, и hqb непосредственного обращения обобщен Смещение системы-это

изменение соответствующих обобщенных координат Q, Q. lfQs-обобщенная сила системы, T-кинетическая энергия системы. Для систем, подчиненных полому насосу, bqy, 8q. поскольку 2i bqs является независимым обобщаемым перемещением, общее уравнение динамики удовлетворяется только условием, что коэффициент, находящийся в возможном перемещении, равен пуле. д ДТ _ ДТ _ ДТ Н йй \ dqt-КЖ> dT_dT_n д ДТ Д d dT dT_ да d’Ant C \ dq3 Ws * д ДТ dT = _dP ДТ б ’ д ы в DQS DQS с ’ * ) Такого рода уравнение Лагранжа класса 1 не рассматривается. Таким образом, приведенное ниже уравнение Лагранжа типа 2 называется просто уравнением Лагранжа. Вводя Лагранжеву функцию Lt, равную разности кинетической

и потенциальной энергий, для L = T — P уравнение (2) принимает вид: д 0L » dl_ » в ^ Йй \ DQL по

’ (3 *） д дл _ дл n ДТ йй, ’dq3 ’ д дл дл _ г ДТ служб DQS DQS с Трудность решения задачи динамики системы материальных точек с 1 степенью свободы заключается, в частности, в успешном выборе соответствующей общей теоремы динамики. Для систем с некоторыми степенями свободы решение задачи значительно сложнее, так как решение задачи требует совместного применения общей теоремы и других кинематических relations. In в таких случаях наиболее удобно использовать уравнение Лагранжа. Уравнение Лагранжа является универсальным методом

для составления дифференциальных уравнений движения материальной точечной системы. Большое преимущество уравнения Лагранжа состоит в том, что при наличии идеальной голономной связи сила реакции связи не учитывается. (При применении других методов решения задачи сила реакции связи должна быть исключена из системы составляющих уравнений при решении задачи.）

Динамика системы уравнений, полученная выше при решении большинства задач, может быть выведена непосредственно с помощью уравнения Лагранжа. В зависимости от условия задачи, когда необходимо найти реакцию связи, уравнение Лагранжа используется для определения точки ускорения системы, применяя принцип освобождения связи к соответствующей массе системы и используя либо теорему общей динамики, либо метод

кинетической статики. При решении задач в динамике, когда нет четкого плана применения тех или иных теорем, необходимо отказаться от использования уравнения Лагранжа. Все вышесказанное не умаляет важности теоремы в целом. Общие теоремы рекомендуется использовать при решении некоторых простых задач динамики (см. главу XI ниже). Составление уравнения Лагранжа следует проводить в следующем порядке: I) определяет число степеней свободы в материальной системе. ’> ) Выберите систему координат и введите число независимых обобщенных координат, равное числу степеней свободы. 3) определяет

обобщенные силы Q, Q, Qs системы, соответствующие выбранным обобщенным координатам. (Процедура расчета обобщенной силы подробно описана в пункте I настоящего раздела.) 4) вычислить кинетическую энергию t системы рассматриваемых материальных точек. 5) найти частные производные кинетической энергии в сумме 。。。 дециграмм Скорость 7) подставьте результаты, полученные в разделах 3, 5 и 6, в уравнение Лагранжа. Проблема 407.Уравнение Лагранжа используется для получения дифференциальных уравнений для вращения твердого тела вокруг неподвижной оси. Решение. Твердое тело, которое вращается вокруг неподвижной оси, имеет 1 градус freedom. In дело в том, что для определения местоположения всех точек достаточно задать

1 параметр, например, угол поворота

заданных при этом возможном смещении： 8-4 = 2 Сус 8? = [Тртп») J Я） к-1 к-я Обобщенная сила Q9 — это коэффициент, который находится в Формуле (2). Q,= X’M ^ a). (3） К 1 ноября. Кинетическая энергия твердого тела вращающегося вокруг неподвижной оси имеет следующий вид Вычислите частную производную кинетической энергии относительно обобщенной скорости ДТ, нет. А затем возьмите производную по времени от результата： д ДТ г Дж \ ДТ с = ’А — Заметим, что кинетическая энергия массы T не зависит от обобщенных координат x, y, z、 ДХ ды-б£ — (о> Формула（2）、（3）、（4）и (3) присваивается системе уравнений Лагр ГHkY> = X 17кг k = I k I fe ^ 1 Он от потенциальной энергии системы в соответствии с соответствующими обобщенными

координатами, т. е. dqi ’ Где r = 1,2,…、 Расчет обобщенных сил материальной системы является одним из ключевых этапов решения задачи с использованием 2-го уравнения Лагранжа. 1. Решение о обобщенной силе может быть осуществлено двумя способами: а)наиболее распространенным приемом является вычисление обобщенной силы в виде коэффициента, выражающего сумму основных действий данной силы и соответствующего обобщенного возможного displacements. In в этом случае расчет обобщенных сил следует проводить в следующем порядке: 1) исследуйте число степеней свободы в рассматриваемой системе масс и выберите

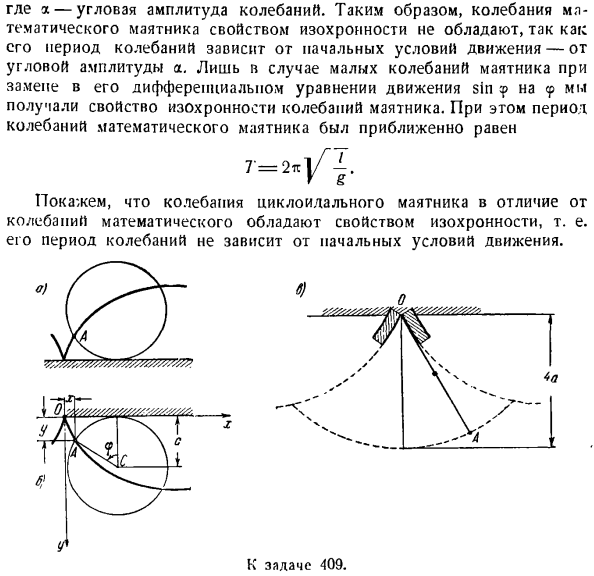
соответствующие обобщенные координаты. 2) показать всю настроенную мощность системы. 3)Если все связи, наложенные на материальную систему, не идеальны, добавьте к данной силе соответствующую реактивную силу связи (силу трения и т.). 4) число обобщенных координат, то есть равное числу степеней свободы в материальной системе, дающее системе независимое обобщенное возможное смещение. Проблема 409.It доказывается изохронизм колебаний циклоидального маятника. Решение. Маятник называется циклоидой и может быть отображен как материальная точка, которая движется по дуге окружности циклоиды. При решении задачи 284 учитывался математический маятник, в котором дуга является орбитой. Дифференциальный звук колебаний математического маятника, записанный в уравнении 284 (4)、 п + £ грех? = 0、 Где о-

угол отклонения маятниковой нити от вертикали, а/ — длина нити. В уравнении (II)той же задачи период колебаний математического маятника г = 2.: Ил(л + Tsinl 2 + элсинт 2-я -••••). Где а-угловая амплитуда колебаний. Таким образом, колебание математического маятника не имеет изохронных свойств, так как его колебательный период зависит от начального состояния движения, то есть от угловой амплитуды a. In в случае малых колебаний маятника, при замене sin дифференциальными уравнениями движения, только

In в этом случае периоды колебаний математического маятника примерно равны Колебания циклоидного маятника указывают на то, что они обладают свойством изохронности, в отличие от математических колебаний. К выпуску 409. Обычное представление о циклоиде связано с локусом точки А, которая находится на краю катящегося колеса без скольжения по рельсу прямой линии (см. рисунок а). Па рисунке б это колесо катится по рельсу на колесе без скольжения снизу. Движение точки А

является колебательным движением, что указывает на то, что ее колебательный период не зависит от начальных условий движения (конструкция циклоидного маятника обсуждается ниже). В качестве обобщенной координаты выберите угол

Единственной указанной силой является масса груза, обозначаемая R. Потенциальная энергия Р массы выражается формулой: Р = ру = — ра ([- а (3） Виде обобщенной силы QF-это скорострельный ЖП. Вводя Формулу (3) выражение в эту формулу: Qv = Pasin

Вычислите частную производную кинетической энергии 7 ’для обобщенной скорости φ. = 2 maq (1-cos и рост нагрузки Б Б. легко видеть, ’3 Поэтому 8R = — р38 (Λ(9） Кинетическая энергия системы T (p! ！- «•с」） Подставляя Формулы (3), (9) и (10) в уравнение Лагранжа (1), получаем дифференциальное уравнение движения лебедки для обобщенной координаты».. ’, / г.\ «О1） (Л + П. ^ + Л +Гротц В случае W: Pj-r^ ускорение груза B направлено вверх. в случае mQPiГ-ha ускорение нагрузки B направлено вниз. п0 = = Pk-ha, лебедка

остановлена, или вся масса движется Равномерно. Направление движения зависит от начальных условий движения. Эта задача также может быть решена с помощью дифференциальных уравнений для вращения твердых тел вокруг неподвижных осей. н / ?= 2 МЗ (ФК)> к = \ Это должно было быть составлено 2 раза.1 для шестерни, другое для остальной электрической ворота. Для Необходимо было мысленно разрушить эту систему в нижней части детали и зубчатой передачи/и 2 точках склеивания, заменив действие отброшенной части конструкции соответствующей реактивной силой сцепления. R, который составляет систему дифференциальных уравнений

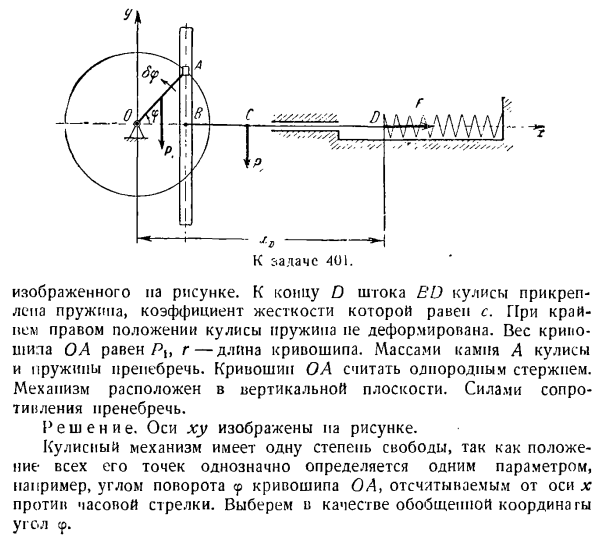
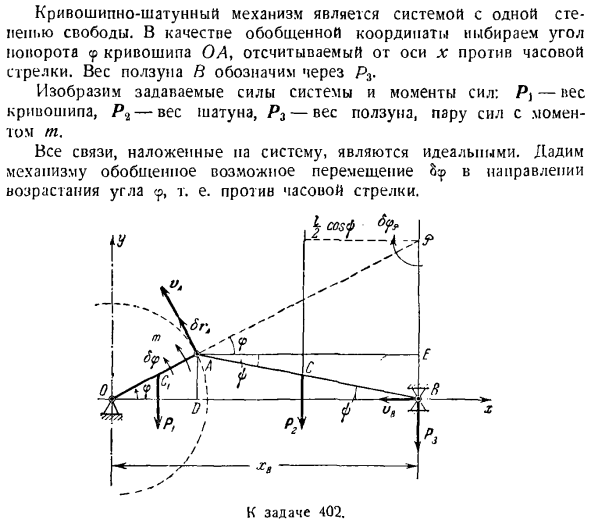
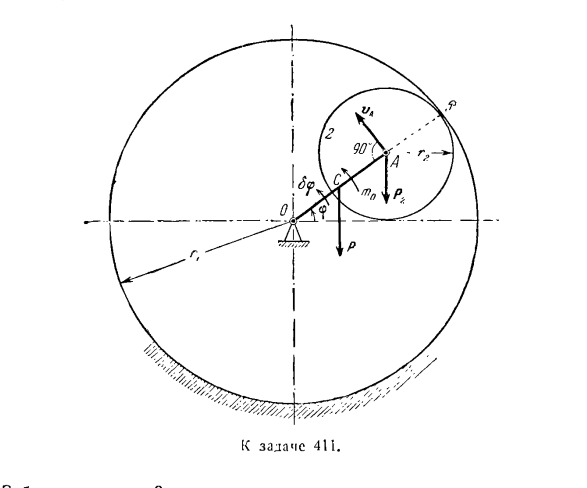
движения, включает в себя силу реакции сцепления. Только после исключения этой силы реакции из результирующей системы уравнений может быть достигнуто уравнение (11).Преимущества уравнения Лагранжа, не содержащего реакции связывания, очевидны. Задача 411.Определите угловое ускорение коленчатого вала в вертикальной плоскости. Шестерня 2 внутренне зацеплена с неподвижной шестерней/.Колесо 2 использует кривошип OA для перемещения гайки, и применяется силовая пара с крутящим моментом от// / 0 до v. Вес кривошипа OA равен P, вес колеса

2 равен g2, радиус колеса 2 равен радиусу неподвижного колеса L Колесо 2 считается однородным круговым диском, а кривошип O / H-влажным однородным стержнем. Игнорируйте сопротивление движению. Решение. Поскольку угол поворота кривошипа ОА определяет все положения, планетарная передача имеет 1 степень свободы. Механизм действия point. As в качестве обобщенной координаты выберите угол 9, измеренный либо по горизонтальной оси, либо против часовой стрелки. Уравнение Лагранжа обобщенных

координат-Р41 0.4 [Кост и R. 0Л= 0&> — — f(3） И затем…

Кинетическая энергия ползучести ОА, вращающейся вокруг неподвижной оси о, перпендикулярной плоскости фигуры, вычисляется по формуле= ^ — О-я-ОА ^ л-т ^ — СБР-момент инерции кривошипа. Так… (4 )） Кинетическая энергия шестерни 2, которая совершает плоское движение Найти скорость точки А, конечную точку кривошипа ОА. ба = \ ОА \ ч =(ГУ-б) х. (6） Рассмотрим скорость той же точки А, которая принадлежит шестерне 2, относительно мгновенного центра относительно скорости колеса. vA = a iP•u = r9sh2. (7 )） Если мы сравним формулы (b) и (7), то увидим следующее: г-г.

Два Момент инерции шестерни 2 рассчитывается по следующей формуле л (9) Если подставить выражения v5, coi и/ d из выражений (6), (8) и (9) соответственно, то выражение (5)будет иметь следующий вид: (У） Уравнения (3), (4) и (10) используются для описания уравнения кинетической энергии планетарного механизма. + *(ВТОРОЙ） Вычислите частную производную кинетической энергии t, но обобщенная скорость равна: dT 2P + NR、 СФ = — ЭИ -» -’»> -?В =(8)я• » А затем возьмите производную по времени от результата： Д ДГ ^ г + ОГ ^» Как- — — — (Т | Р потому выражение (9), ХС = rcos СР +(1–4 +1 х * соѕ 2? ）、 Иначе говоря = Ж + р так? + ’8′); 2 / cos Откуда ■ * С = — Р(грех 9-(—^- х Sin 29 ^ 9.(11） Центр тяжести кривошипа и шатуна ОА расположен на их средней точке и имеет такую же ординату в конструкции Нам = язык yct = 2-си » б Откуда —

’Р£соѕ (О.- Если ввести значение xc и усов из Формулы (10) в формулы (11) и (12), то вы увидите следующее: В * = РМ(грех 9 + т х Sin 2?V-Ч Т потому что * * 9 (13 )） Формула (G) для Формулы ma и формулы (P) и (13） П /- И. Учитывая то, что мы получаем： g»»: = <3 [4 (грех?- Ф-ТХ грех + коси *] + Потому что — . потому что 2 + р *>с°с » С. От (21） Где/ pr определяется выражением

(18).Формула (21) представляет собой дифференциальное уравнение для движения кривошипно-шатунного механизма. Задача 399.Определить обобщенную силу в случае движения математического маятника массы р, Если длина нити равна/.Для обобщенных координат возьмем угол отклонения

При решении обратной задачи, то есть при определении движения заданной силой, часто используется численное интегрирование, так как решение дифференциального уравнения (21) затруднено. В зависимости от состояния задачи необходимо определить закон изменения крутящего момента M. Это позволяет получить равномерный кривошип Bpauienne, или cf. Далее, она равна 3 = 0, и решение уравнения (21) относительно m дает следующий результат: Куда? + Xsin 2?(С COS Так как кинетическая энергия material материальной системы, определяемая формулой (13), не зависит от обобщенных координат cp и S.、 ДТ ДГ л （4）、（5）、（14）、подставляя и(15)в уравнение Лагранжа(1), получаем: Р + 12Р,+ 2Р, м-2Р, Р.? +£Шя (4П | п, П3）、 (16） — ?■^§- Ф Р? = Приблизительно. 1.Е Р Решая одновременно уравнения (5 и S) (16), можно видеть: = r—H aor,-h (jp, −2 /> TG ’ (Inlex

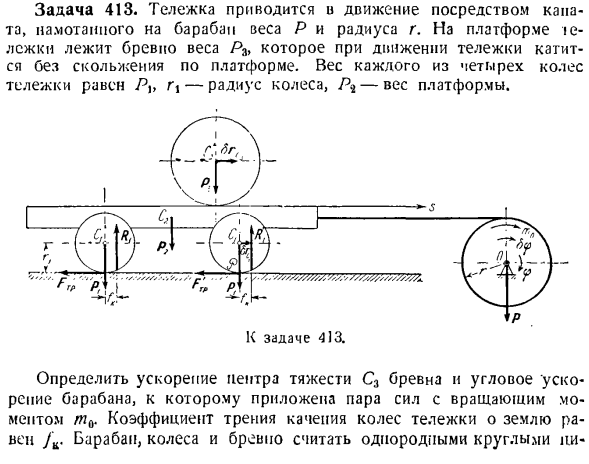
CP с обобщенной силой Q является координатой(ЛРН * — •3/л, — / — 2×3)^ ’о — / тр-н-б Р2 4 * па） o_9 а _ _ _ / 2 (При выводе этих уравнений предполагается, что/ = 0 a = s = 0.) Задача 414.Решите задачу 396, используя уравнение Лагранжа. Solution. In решая задачу 396, было показано, что рассматриваемая система имеет 2 степени свободы. В качестве обобщенной координаты возьмем линейную координату 5 |傾斜面に沿って下方に向けられたs. lt запишите уравнение Лагранжа для обобщенных координат S.< ±dT_dT_p Д ДГ г dtdli 3s] — Дидди; Ди、〜 Заранее поставленная сила:Т 7 Рг2 10 = — так、 Кинетическая энергия постепенно движущейся платформы принимает форму −2 г в•

Учитывая, что, учитывая нерасширяемость веревки a=, вы можете увидеть следующее: =(8） Колесо вагонетки сделает квартиру motion. So … R G Если момент инерции колеса равен/, = вращать — Я ЗГ. виртуальный канал Без проскальзывания vr = 5.Резьбовой стержень Ы ы ы ы Тельпо. J [если подставить значение этого vc в выражение (I)、 744)= 1.&r V + J ^ + £ (, 2） (6) Формула（7）、（8）、（9）и (12) к/(1), 7 ’(i \ T < Так как кинетическая энергия material материальной системы, определяемая формулой (13), не зависит от обобщенных координат cp и S.、 ДТ ДГ л （4）、（5）、（14）、подставляя и(15)в уравнение Лагранжа(1), получаем: Р + 12Р,+ 2Р, м-2Р, Р.? +£Шя (4П | п, П3）、 (16） — ?■^§- Ф Р? = Приблизительно. 1.Е Р Решая одновременно уравнения (5 и S) (16), можно видеть: = r—H aor,-h (jp, −2 />TG ’ (Inlex CP с обобщенной силой Q является координатой(ЛРН * — •3/л, — / — 2×3)^ ’о — / тр-н-б Р2 4 * па） o_9 а _ _ _ / 2 (При выводе этих уравнений

предполагается, что/ = 0 a = s = 0.) Задача 414.Решите задачу 396, используя уравнение Лагранжа. Solution. In решая задачу 396, было показано, что рассматриваемая система имеет 2 степени свободы. В качестве обобщенной координаты возьмем линейную координату 5 |傾斜面に沿って下方に向けられたs. lt запишите уравнение Лагранжа для обобщенных координат S.< ±dT_dT_p Д ДГ г dtdli 3s] — Дидди; Ди、〜 Заранее поставленная сила:

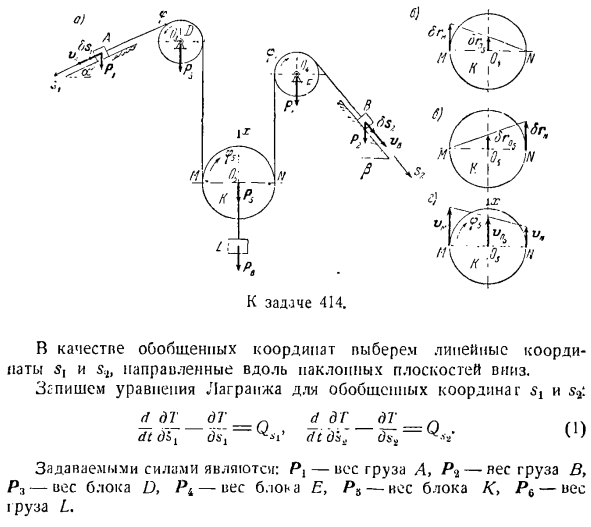
Все соединения, наложенные на систему, идеальны (так как наклонная плоскость должна быть идеально гладкой, на оси блока нет трения, а нити не растягиваются и не растягиваются). Для определения обобщенных сил QH и Q $ 2 приведем нагрузки A и B, соответственно, возможные перемещения SSj и направление, направленное параллельно линии максимального наклона наклонной плоскости в направлении увеличения координаты s.、％ Чтобы вычислить обобщенную силу QS, мы даем системе обобщенное возможное смещение Ss, предполагая, что [lsq равен нулю. Φ0,=(это

возможно, потому что » и ’ в являются независимыми обобщенными координатами.） Поэтому правая ветвь потока от нагрузки B, блока E и нагрузки B до точки N останавливается. Точка м нити получает вертикальное восходящее возможное движение Lm, размер которого равен Ss, поскольку нагрузка а может перемещаться вниз из-за отсутствия удлинения нити. Определите возможное смещение оси блока Sr0, принимая во внимание, что точка/ V нити накала остается в покое в то же время (см. Рисунок B).Это равно половине модуля модульно-способного перемещения 8gL1, то есть Ох 2.2 * Ж Рассчитайте сумму работы сил, приведенных к обобщенным

8 секундам, возможное перемещение точек системы, соответствующее возможному перемещению груза А. (В БА = РХ грех aZsi-(РВ + П6) б Рассматривая Формулу(2), можно увидеть: ал = [Р, грех-я(/> т + /> я)] та. (3） Гравитационная работа п. 2 равна пулевой, т. к.= 0, поэтому работы гравитации Р3 и Р4 равны нулю, т. к. точки приложения этих сил не перемещаются. Обобщенная сила QS1-это коэффициент, который находится в обобщенном возможном смещении уравнения (3). Под рукой-грех-у(П5 + П6). (Ля） Чтобы вычислить обобщенную силу Q $ 2, Дайте системе обобщенное возможное смещение Is, предполагая, что ОС равна пуле. Это

означает, что блок D груза а и левая ветвь нити а груза а находятся в точке М нити. Из-за нерастяжительного характера винта, из-за возможного перемещения нагрузки на ПА, точка N винта Излучает возможное смещение L ^вверх в вертикальном направлении. Это считается смещением и С. 3. размер равен модулю упругости. Учитывая, что точка нити M неподвижна в то же время, она выглядит так (см. Рисунок C）\ ^ О3 = =(5） Обобщенные возможные перемещения вычисляют сумму работы заданных сил на возможные перемещения точек системы, соответствующих ос4： BA = P,^ sin ft — (Pe + Pb) если рассматривать уравнение (5)、 БА = [Р4 грех? -я (П8-Ф Р6)] СУ4. (си） Работа гравитации Pt равна нулю, потому что s = 0.Работа

гравитации P3 и P4 равна нулю, так как их точки приложения неподвижны. Обобщенная сила QSi является коэффициентом в уравнении (6) os4. Вопрос, с = P4sin?^ Я(ЧП + П6). (7 )） Переходим к расчету кинетической энергии t материальной системы, состоящей из 6 масс: блоков D, E, K, A, B, L： м = ро ОКБ) 7(ч) Пи)пн _ [_ ППГ(г） Скорости нагрузки A и 8 fl направлены параллельно линиям максимального наклона наклонной плоскости. Проекция этих скоростей на ось s будет равна sx и s соответственно.2. Радиус блока D, E, K обозначается через r3, r4 и guard. In в этом случае угловые

скорости блоков O и E выражаются следующим образом: (9 )） Из-за не масштабируемости нити скорость Vm точки нити M равна скорости vA груза A. R>Λ1¥=£,.Аналогично: v / Wx = 9. использование рисунка очень просто. g, найти скорость движения оси Ov блока K>do plane motion： (10 )） Девять в Два Два Чтобы определить угловую скорость блока K, найдите скорость точки M и получите точку / V полюсов. Иначе говоря (vMN) x = 1 MN \ = 2rv£6, 2r3 ’?3 = .поскольку это v, угловая скорость блока равна K’. Кинетическая энергия груза а и в、 = 1 5. .В.], (П2） Рассчитайте кинетическую энергию блоков D

и E, которые вращаются вокруг неподвижной оси. Т© — 1 / А2 Т <Я>— я СВ2 1-2 пр™ » = 2 (Р р г р р р- \ = .: = Т ^ Дж Используя формулу(9) можно увидеть: Кинетическая энергия блока K, который совершает плоское движение, определяется уравнением Т [п) ВХ — / м 2 г 2 Подставляя значение момента инерции блока к、 Формула называется (10) и (11) и вы получаете: Кинетическая энергия постепенно движущейся нагрузки L равна、 Нравится 7 ’©=.- !-7) 0.. 2(г Примените формулу (10) для определения: 74.)= я J

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

источники:

http://lfirmal.com/uravnenie-langranzha-vtorogo-roda/