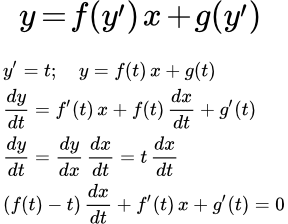Дифференциальное уравнение Лагранжа
Решение дифференциального уравнения Лагранжа
Рассмотрим дифференциальное уравнение Лагранжа:
(1) ,
где и – это функции.
Будем искать его решение в параметрическом виде. То есть будем считать, что , , а также производная являются функциями от параметра . Положим
.
Поставим в (1):
(2) .
Продифференцируем по :
(3) .
С другой стороны:
(4) .
Левые части уравнений (3) и (4) равны. Приравниваем правые части и выполняем преобразования:
;
.
Разделим на . При уравнение принимает вид:
.
Это линейное дифференциальное уравнение относительно переменной . Решая его, получаем зависимость переменной от параметра : . Затем подставляем в (2):
.
В результате получаем зависимость переменной от параметра : . То есть мы получили параметрическое представление решения уравнения (1).
Дополнительные решения дифференциального уравнения Лагранжа
В процессе приведения уравнения к линейному, мы разделили уравнение на . Поэтому мы рассматривали решение при . В заключении следует рассмотреть случай , то есть исключить параметр из уравнений:
(5) ;
(6) .
Уравнение (5) содержит только переменную t . Поэтому его нужно решить и определить корни. Если корней нет, то дополнительных решений также нет.
Предположим, что мы нашли корни уравнения (5) (один или несколько). Обозначим такой корень как :
(7) .
Тогда уравнение (6) дает нам зависимость y от x , которая является линейной функцией:
.
Поскольку в силу (7), , то
(8) .
Покажем, что (8) является решением исходного уравнения (1). Для этого найдем производную (8). Она равна постоянной:
.
Подставим (8) и в (1):
;
;
.
Это уравнение выполняется, поскольку в силу (7), .
Таким образом, мы нашли, что уравнение (1) может иметь решения
,
где – корни уравнения
.
Пример
Решить уравнение:
(1.1)
Разделим на . При имеем:
(1.2) .
Это уравнение Лагранжа. Ищем решение в параметрическом виде. Считаем, что , , а также — это функции от параметра . Положим . Тогда
(1.3) .
Чтобы упростить выкладки, умножим (1.3) на знаменатель дроби и продифференцируем по :
;
;
(1.4) .
Далее имеем:
(1.5) .
Поставляем (1.3) и (1.5) в (1.4) и выполняем преобразования:
;
;
.
Разделим на . При ( или при и при ) имеем:
.
Разделяем переменные и интегрируем:
;
;
.
Потенцируем:
.
Заменим постоянную . Знак модуля сводится к умножению на постоянную ±1, которую включаем в .
.
Отсюда
;
.
Подставляем в (1.3):
.
Заменим постоянную :
.
Теперь рассмотрим значения , которые мы исключили из рассмотрения при выполнении операций деления. Для этого подставим эти значения в исходное уравнение (1.1),
(1.1) .
Проверим, существует ли для этих значений дополнительные решения.
1) Подставим в (1.1):
.
Отсюда . Решение удовлетворяет исходному уравнению (1.1).
2) Подставим в (1.1):
;
.
Значение не удовлетворяет исходному уравнению. Отбрасываем его.
3) Подставим в (1.1):
;
;
.
Решение удовлетворяет исходному уравнению.
Общее решение уравнения имеет вид:
;
;
.
Автор: Олег Одинцов . Опубликовано: 26-08-2012 Изменено: 24-11-2021
Уравнение Лагранжа
Вы будете перенаправлены на Автор24
Общий метод решения уравнения Лагранжа
Предположим, что некоторое дифференциальное уравнение первого порядка $F\left(x,y,y’\right)=0$, не разрешенное относительно производной, удалось разрешить относительно $y$, то есть представить в виде $y=f\left(x,y’\right)$.
Частным случаем дифференциального уравнения такого вида является уравнение Лагранжа $y=x\cdot \phi \left(y’\right)+\psi \left(y’\right)$, в котором $\phi \left(y’\right)\ne y’$.
Дифференциальное уравнение Лагранжа решают методом введения параметра $y’=p$.
При этом исходное дифференциальное уравнение можно переписать в виде $y=x\cdot \phi \left(p\right)+\psi \left(p\right)$.
Выполнив дифференцирование по $x$ с учетом $dy=p\cdot dx$, после несложных алгебраических преобразований получаем линейное дифференциальное уравнение относительно функции $x\left(p\right)$ и её производной $\frac
Это уравнение решается известным методом, в результате чего получим его общее решение $x=F\left(p,C\right)$.
Подставив полученный результат в соотношение $y=x\cdot \phi \left(p\right)+\psi \left(p\right)$, получим $y=F\left(p,C\right)\cdot \phi \left(p\right)+\psi \left(p\right)$.
Дополнительные частные либо особые решения уравнения Лагранжа могут быть получены в результате нахождения действительных корней уравнения $p-\phi \left(p\right)=0$ и подстановки их в $y=x\cdot \phi \left(p\right)+\psi \left(p\right)$.
Решение типичных задач
Решить дифференциальное уравнение $y=-x\cdot y’+y’^ <2>$.
Имеем дифференциальное уравнение Лагранжа, в котором $\phi \left(y’\right)=-y’$ и $\psi \left(y’\right)=y’^ <2>$.
Вводим параметр $y’=p$ и получаем $y=-x\cdot p+p^ <2>$, а также $\phi \left(p\right)=-p$ и $\psi \left(p\right)=p^ <2>$.
Теперь получим уравнение вида $\frac
Уравнение приобретает вид: $\frac
Применяем алгоритм решения линейного неоднородного дифференциального уравнения:
- Стандартный вид $\frac
+\frac<1><2\cdot p>\cdot x=1$, где $P\left(p\right)=\frac<1><2\cdot p>$, $Q\left(p\right)=1$. - Вычисляем интеграл $I_ <1>=\int P\left(p\right)\cdot dp =\int \frac<1><2\cdot p>\cdot dp =\frac<1><2>\cdot \ln \left|p\right|$.
Записываем частное решение $v\left(p\right)=e^<-\frac<1> <2>\cdot \ln \left|p\right|> $, выполняем упрощающие преобразования: $\ln v\left(p\right)=-\frac<1> <2>\cdot \ln \left|p\right|$; $\ln \left(v\left(p\right)\right)^ <2>+\ln \left|p\right|=0$; $\left(v\left(p\right)\right)^ <2>\cdot \left|p\right|=1$.
Выбираем для $v\left(p\right)$ простейший ненулевой вариант: $v\left(p\right)=\frac<1> <\sqrt
> $.
\cdot dp =\frac<2><3>\cdot p^<\frac<3><2>> $ и получаем $u\left(p,C\right)=\frac<2><3>\cdot p^<\frac<3><2>> +C$.
> =\frac<2><3>\cdot p+\frac > $. Подставляем полученный результат в $y=x\cdot \phi \left(p\right)+\psi \left(p\right)$. Получаем: $y=-\left(\frac<2> <3>\cdot p+\frac > \right)\cdot p+p^ <2>=\frac<1> <3>\cdot p^ <2>-C\cdot \sqrt $. Таким образом, общее решение данного уравнения Лагранжа в параметрической форме имеет вид: $\left\<\begin > > \\ > \end Для определения дополнительных частных либо особых решений находим корни уравнения $p-\phi \left(p\right)=0$: получаем $p=0$. Подставляем $p=0$ в $y=-x\cdot p+p^ <2>$ и получаем $y=0$. Это решение является частным, так как получается из общего при $C=\frac<1> <3>\cdot p^<\frac<3> <2>> $. Решить дифференциальное уравнение $y=x\cdot y’\cdot \left(y’+2\right)$. Имеем дифференциальное уравнение Лагранжа, в котором $\phi \left(y’\right)=y’\cdot \left(y’+2\right)$ и $\psi \left(y’\right)=0$. Вводим параметр $y’=p$ и получаем $y=x\cdot p\cdot \left(p+2\right)$, а также $\phi \left(p\right)=p\cdot \left(p+2\right)$ и $\psi \left(p\right)=0$. Теперь получим уравнение вида $\frac Уравнение приобретает вид: $. \cdot dp =2\cdot \ln \left|p\right|$. Подставляем полученный результат в $y=x\cdot p\cdot \left(p+2\right)$. Получаем: $y=\frac \right)$. Таким образом, общее решение данного уравнения Лагранжа в параметрической форме имеет вид: $\left\<\begin \right)> \end Параметр $p$ из этой системы можно исключить: $p=\frac <\sqrt Для определения дополнительных частных либо особых решений находим корни уравнения $p-\phi \left(p\right)=-p^ <2>-p=0$. Получаем: $p\cdot \left(p+1\right)=0$, откуда имеем два корня $p=0$ и $p=-1$. Подставляем первый корень $p=0$ в $y=x\cdot p\cdot \left(p+2\right)$ и получаем первое дополнительное решение данного уравнения $y=0$. Это решение является частным, так как получается из общего при $C=0$. Подставляем второй корень $p=-1$ в $y=x\cdot p\cdot \left(p+2\right)$ и получаем второе дополнительное решение данного уравнения $y=-x$. Это решение является особым, так как не получается из общего ни при каком $C$. В этой статье мы попробуем разобраться с такой темой, как «Уравнения Лагранжа». Вообще, уравнения Лагранжа довольно полезная штука, например, на их основе решаются задачи на малые колебания. В МГТУ им. Баумана в третьем семестре предлагается самостоятельное домашнее задание, в котором нужно записать уравнения Лагранжа для системы с двумя степенями свободы. Итак, типовое задание выглядит так. Итак, приступим к решению. Поскольку обобщенных координат две (две степени свободы), система уравнений Лагранжа будет выглядеть так: С угловой скоростью катка тоже все понятно. Так как проскальзывание отсутствует Самое трудное — выразить скорость шарика 1. Как мы уже говорили, он совершает сложное движение, значит, его скорость складывается из относительной и переносной. Переносная — это скорость поступательного движения призмы 3. Относительное — скольжение вдоль паза 2, которое описано координатой S. Значит Векторно складываем эти две скорости Второе выражение здесь — это теорема косинусов. Если нанести все векторы на рисунок, станет понятно, почему так. Определившись со скоростями, записываем выражение для кинетической энергии системы Т. Полная кинетическая энергия складывается из кинетических энергий всех тел, обладающих массой. То есть в нашем случае, тел 1, 3, 5. Шарик 1 обладает энергией Призма 3 движется поступательно Каток 5 совершает плоское движение, так что его кинетическая энергия складывается из энергии поступательного и вращательного движений Полная кинетическая энергия системы Для записи уравнений Лагранжа это выражение нужно несколько раз продифференцировать. Сначала по координате x. Частные производные Производную по x с точкой дифференцируем по времени Теперь то же самое по координате S. Частные производные Производная по времени Левая часть уравнений Лагранжа готова. Займемся правой частью. Для нее нужно посчитать обобщенные силы по каждой координате. Есть несколько способов это сделать, мы предпочитаем делать это через элементарную работу на малом приращении координаты. В общем случае формула выглядит так На практике это применяется следующим образом. Сначала нанесем на рисунок все действующие силы. В нашем случае это сила упругости пружины и силы тяжести. Сначала считаем обобщенную силу по координате x. Для этого мысленно «замораживаем» координату S, и позволяем системе свободно двигаться по координате x. То есть шарик «приклеивается» к пазу 2, и внутри него никуда не движется. Все перемещение происходит по координате x. Очевидно, что сила упругости работу не совершает, так как ее длина не меняется. Очевидно, что силы тяжести работу не совершают, так как движение происходит горизонтально. Официальным языком это записывается так Теперь обобщенная сила по координате S. Мысленно «замораживаем» координату x. Получается, что призма 3 вместе с пазом 2 и катком 5 стоит на месте, а внутри неподвижного паза движется шарик. Сила упругости совершает работу, также как и сила тяжести шарика 1. Пружина была растянута на величину статической деформации δ и дополнительно растянута на S в произвольный момент времени, то есть сила упругости равна с·(δ+S). Работа силы упругости отрицательна, так как пружина растягивается. Работа силы тяжести шарика 1 положительна, так как шарик движется вниз. Силы тяжести призмы 3 и катка 5 работу не совершают, так как эти тела покоятся. Получаем Собственно, все. Собираем все посчитанные величины в уравнения Лагранжа и получаем систему дифференциальных уравнений, описывающих движение системы. Для проверки можно посмотреть размерности, в обеих частях выражения размерности должны совпадать (обычно это ньютоны). Конечно, разные задачи немного отличаются в ходе решения, но алгоритм всех задач примерно такой. 1) Определить число степеней свободы и выбрать обобщенные координаты 2) Записать уравнения связей 3) Записать выражение для кинетической энергии 4) Взять необходимые производные 5) Записать обобщенные силы по каждой координате 6) Записать уравнения Лагранжа Если что-то не получается, не отчаивайтесь, мы всегда рады помочь. http://spravochnick.ru/matematika/differencialnye_uravneniya/uravnenie_lagranzha/ http://botva-project.ru/botva/obrazovanie/teoreticheskaya-mehanika-uravneniya-lagranzha/Готовые работы на аналогичную тему
Теоретическая механика. Уравнения Лагранжа
Прежде чем броситься решать эту задачу, посмотрим на задание и проанализируем его. Есть призма 3, которая движется поступательно по горизонтальной плоскости без трения. В призме сделан паз 2, по которому движется шарик 1. Если вы помните темы прошлого семестра, то легко увидите, что шарик совершает сложное движение — переносное поступательное вместе с призмой 3 и относительное поступательное по пазу 2. Далее есть стержень 4, который соединяет призму и каток 5. Очевидно, что скорость центра катка С равна скорость призмы. Каток движется без скольжения, это важный момент. Движение системы описывается двумя обобщенными координатами, которые любезно выбрал для нас составитель задания.
Расчет начинаем с записи уравнений связи — выражаем скорости всех ключевых точек и тел, имеющих массу, через обобщенные координаты. Из сказанного ранее понятно, что нам понадобится линейная скорость призмы 3, линейная скорость катка 5, угловая скорость катка 5 и скорость шарика 1. С поступательным движением все просто
