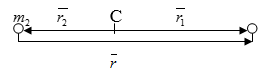Уравнение ламберта задачи двух тел

Ошибка
404

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Задача двух тел

Вы будете перенаправлены на Автор24

Приведенная масса

Решение уравнений динамики системы материальных точек встречает непреодолимые математические трудности, т.к. точного решения этих уравнений для произвольных сил не найдено уже в случае трех материальных точек.

В связи с этим важна задача о замкнутой системе двух точек, называемая задачей двух тел. Она имеет простое и исчерпывающее решение — сводится к основной задаче динамики одной материальной точки. Решение задачи двух тел используется в небесной механике, описывающей движение планет и их спутников в Солнечной системе, в задачах на столкновение частиц, в статистической физике и других вопросах.

Рассмотрим замкнутую систему двух материальных точек, взаимодействующих между собой. Как известно центр масс такой системы движется равномерно и прямолинейно (или покоится). Задача просто решается в системе с началом в центре масс, движущейся поступательно (такая система называется Ц-системой).

Обозначим массы частиц через $m_ <1>$ и $m_ <2>$ и их радиус-векторы, проведенные от центра масс, соответственно $\overline >$ и $\overline >$. Пусть $\overline$- вектор, проведенный от точки $m_ <2>$ к $m_ <1>$. Из определения радиус-вектора центра масс имеем:

Непосредственно из рисунка следует соотношение между радиус-векторами:

$\overline_ <1>=\overline_ <2>+\overline$. (1)

Два последних равенства позволяют выразить радиус-векторы $\overline >$ и $\overline >$ через вектор $\overline$, соединяющий точки $m_ <2>$ и $m_ <1>$. Имеем:

Запишем основные уравнения для движения обеих точек в Ц-системе:

Силы в уравнениях (3) зависят от расстояния между точками, а не от расстояния до центра масс, т.е. решать уравнения (1) отдельно для каждой точки нельзя.

Готовые работы на аналогичную тему

Пользуясь выражениями для радиус-векторов (2), исключим из основных уравнений (3) $\overline >$ и $\overline >$. Тогда получаем уравнения движения:

Так как по третьему закону Ньютона $\overline_ <2,1>(r)=-\overline_ <1,2>(r)$, оба уравнения становятся тождественными, и движение системы двух точек, в результате их взаимодействия эквивалентно движению одной точки в соответствии с уравнением:

Уравнение (4) отличается от известного уравнения движения материальной точки в поле заданной силы только тем, что вместо массы $m$здесь выступает комбинация масс двух точек:

Величина $m’$ называется приведенной массой.

Итак, задача двух тел свелась к задаче о движении одной материальной точки с приведенной массой в Ц-системе под действием центральной силы; уравнение движения имеет обычный вид:

Но при использовании результатов решения уравнения (6) необходимо помнить, что точка $m’$, движущаяся на конце радиус-вектора $\overline$под действием силового центра в начале координат Ц-системы, является не реальной, а изображающей движение системы. От ее движения, после того как уравнение (6) проинтегрировано, следует переходить к реальному движению двух материальных точек $m_ <2>$ и $m_ <1>$.

Движение двух материальных точек в системе центра масс

Движение изображающей точки в соответствии с уравнением (6) будет плоским. Пусть кинематическое уравнение движения найдено: $\overline=\overline(t)$.

В таком случае с помощью формулы (2) находим кинематическое уравнение движения обеих материальных точек в Ц-системе:

Очевидно, что траектория движения изображающей точки и точек $m_ <2>$ и $m_ <1>$ будут подобными кривыми относительно центра масс, а отношение подобия есть обратное отношение масс, т.е.:

Нетрудно найти и скорости движения точек. Дифференцируя (7) по времени, имеем:

Задача двух тел решена.

Момент импульса для системы двух точек имеет вид: $\overline=m_ <1>\left|\overline_ <1>\overline_ <1>\right|+m_ <2>\left|\overline_ <2>\overline_ <2>\right|$. Необходимо записать выражение для собственного момента импульса системы через приведенную массу.

Момент импульса системы двух точек: $\overline=m_ <1>\left|\overline_ <1>\overline_ <1>\right|+m_ <2>\left|\overline_ <2>\overline_ <2>\right|$.

Найти: собственный момент импульса системы — ?

Момент импульса системы двух точек:

\[\overline=m_ <1>\left|\overline_ <1>\overline_ <1>\right|+m_ <2>\left|\overline_ <2>\overline_ <2>\right|.\]

Внесем сюда выражения $\overline >$ и $\overline >$через вектор $\overline$, выражающийся формулой (7) и получим равенство:

\[\overline=\frac m_ <2>> +m_ <2>> \left|\overline\overline_ <1>\right|-\frac m_ <2>> +m_ <2>> \left|\overline\overline_ <2>\right|=\frac m_ <2>> +m_ <2>> (\overline\left|\overline_ <1>-\overline_ <2>\right|).\]

Вектор $\overline_ <1>-\overline_ <2>$ есть скорость $\overline$первой частицы относительно второй или скорость изображающей точки $\overline$ и окончательный результат выражается равенством:

Ответ: собственный момент импульса системы $\overline=m'[\overline\overline<\cdot v>]$

задача о движении двух тел сводится к задаче о движении одной точки под действием заданной силы;

особую роль при этом играет приведенная масса системы, через нее выражаются основные динамические параметры системы — энергия, импульс, момент импульса.

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 06 04 2021