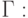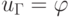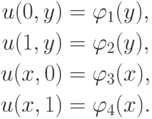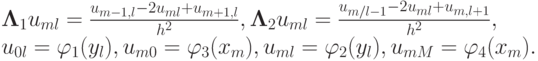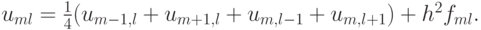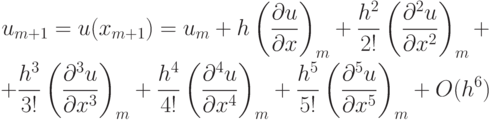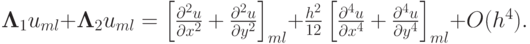Уравнение лапласа численный метод решения

Численное решение уравнений в частных производных эллиптического типа на примере уравнений Лапласа и Пуассона

Среди всех типов уравнений математической физики эллиптические уравнения с точки зрения вычислителей стоят особняком. С одной стороны, имеется хорошо развитая теория решения эллиптических уравнений и систем. Достаточно легко доказываются теоремы об устойчивости разностных схем для эллиптических уравнений. Во многих случаях получаются априорные оценки точности расчетов и числа итераций при решении возникающих систем сеточных уравнений . С другой стороны, системы сеточных уравнений , возникающие при решении уравнений методами сеток, имеют большую размерность и плохо обусловлены. Для решения таких систем разработаны специальные итерационные методы .

6.1. Постановка задачи. Простейшая разностная схема «крест». Устойчивость схемы «крест»

Будем рассматривать двухмерное уравнение Пуассона

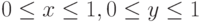
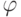
в единичном квадрате с краевыми условиями первого рода на границе расчетной области

( — заданная на границе функция ).

В случае прямоугольной области граничные условия удобно записать в следующем виде:

Для простоты выкладок введем равномерную расчетную сетку с узлами m, y_l> , m, l = 0, 1, . , M с равным количеством шагов по каждому пространственному направлению, сеточную область D — совокупность всех узлов сетки, включая граничные, и сеточную функцию < u_ml >. В этом случае шаги по координатам предполагаются равными. В случае неравных шагов по каждому направлению полученные результаты не изменятся, а запись уравнений станет более громоздкой.

Выбираем простейший пятиточечный шаблон разностной схемы «крест» . На этом шаблоне аппроксимирующее разностное уравнение легко выписать. Для этого производные заменим вторыми разностями:

где h — шаг по координатам, или в операторной форме

Эту же разностную схему можно записать в каноническом виде для разностных схем для эллиптических уравнений:

Такую каноническую запись не следует путать с канонической формой записи итерационного метода, которая встретится ниже.

Такая схема обладает вторым порядком аппроксимации по обеим координатам. Это легко показать, применяя разложение в ряд Тейлора функции — проекции точного решения на сетку — вплоть до членов четвертого порядка включительно. Проведем такое разложение для одного из операторов, стоящих в данном разностном уравнении:

Здесь учтено разложение проекции точного решения в ряд Тейлора

и аналогичное разложение для u_{m — 1}.

Для рассматриваемого двухмерного уравнения получим выражение для главного члена невязки

Рассмотрим устойчивость полученной схемы. Отметим, что методы исследования на устойчивость , применяемые для эволюционных (зависящих от времени) уравнений, здесь не работают. Действовать приходится на основе определения устойчивости.

Сформулируем и докажем две леммы, которые облегчат процедуру доказательства устойчивости разностной схемы.

Уравнение Лапласа

Многие стационарные физические задачи, т.е. такие, в которых рассматриваются явления, неизменные с течением времени (исследования потенциальных течений жидкости, определение формы нагруженной мембраны, задачи теплопроводности и диффузии в стационарных случаях и др.) сводятся к решению уравнения Пуассона вида

(2.88)

Если , то уравнение (2.88) называется уравнением Лапласа. Для простоты будем рассматривать двумерное уравнение Лапласа

(2.89)

Решение этого уравнения будем искать для некоторой ограниченной области Gизменения независимых переменных х, у. Границей области Gявляется замкнутая линия L. Для полной формулировки краевой задачи кроме уравнения Лапласа нужно задать граничное условие на границе L. Примем его в виде

(2.90)

Задача, состоящая в решении уравнения Лапласа (или Пуассона) при заданных значениях искомой функции на границе расчетной области, называется задачей Дирихле.

Одним из способов решения стационарных эллиптических задач, в том числе и краевой задачи (2.89), (2.90), является их сведение к решению некоторой фиктивной нестационарной задачи (гиперболической или параболической), найденное решение которой при достаточно больших значениях времени tблизко к решению исходной задачи. Такой способ решения называется методом установления.

Поскольку решение U(x,y) уравнения (2.89) не зависит от времени, то можно в это уравнение добавить равный нулю (при точном решении) член ¶U/¶t. Тогда уравнение (2.89) примет вид

(2.91)

Это известное нам уравнение теплопроводности, для которого в разд. 2.3.2, 2.3.3 уже строили разностные схемы. Остается только задать начальное условие. Его можно принять практически в произвольном виде, согласованном с граничными условиями. Примем

(2.92)

Граничное условие (2.90) при этом остается стационарным, т. е. не зависящим от времени.

Процесс численного решения уравнения (2.91) с условиями (2.92), (2.90) состоит в переходе при t→∞ от произвольного значения (2.92) к искомому стационарному решению. Счет ведется до выхода решения на стационарный режим. Естественно, решением ограничиваются при некотором достаточно большом t, если искомые значения на двух последовательных слоях совпадают с заданной степенью точности.

Метод установления фактически представляет итерационный процесс решения задачи (2.91) с условиями (2.92), (2.90), причем на каждой итерации значения искомой функции получаются путем численного решения некоторой вспомогательной задачи. В теории разностных схем показано, что этот итерационный процесс сходится к решению исходной задачи, если такое стационарное решение существует.

Другой способ решения задачи Дирихле состоит в построении разностной схемы путем аппроксимации уравнения (2.89). Введем в прямоугольной области Gсетку с помощью координатных прямых х = const и у = const. Примем для простоты значения шагов по переменным х и у равными h(предполагается, что стороны области Gсоизмеримы). Значения функции Uв узлах (xi, yj) заменим значениями сеточной функции uij. Тогда, аппроксимируя в уравнении (2.89) вторые производные с помощью отношений конечных разностей, получим разностное уравнение (шаблон изображен на рис. 2.27).

(2.93)

Рис. 2.27. Шаблон для уравнения Лапласа

С помощью данного уравнения можно записать систему линейных алгебраических уравнений относительно значений сеточной функции в узлах в виде

(2.94)

Значения сеточной функции в узлах, расположенных на границе расчетной области, могут быть найдены из граничного условия (2.90):

В теории разностных схем доказывается, что решение построенной разностной задачи существует, а сама схема устойчива.

Перейдем теперь, к практическому вычислению искомых значений, т.е. к решению системы (2.94). Каждое уравнение системы (за исключением тех, которые соответствуют узлам, расположенным вблизи границ) содержит пять неизвестных. Одним из наиболее распространенных методов решения этой системы линейных уравнений является итерационный метод. Каждое из уравнений записываем в виде, разрешенном относительно значения uij в центральном узле (см. рис. 2.27):

(2.95)

Алгоритм решения задачи Дирихле с использованием итерационного метода Гаусса-Зейделя решения системы разностных уравнений (2.95) изображен на рис. 2.28. В алгоритме предусмотрен выбор начальных значений uij. Иногда полагают, что uij=0 для всех i, j.

Рис. 2.28. Алгоритм решения задачи Дирихле

Итерационный процесс контролируется максимальным отклонением М значений сеточной функции в узлах для двух последовательных итераций. Если его значение достигнет некоторого заданного малого числа ε,итерации прекращаются и происходит вывод результатов.

Рассмотренные разностные схемы метода сеток используют конечно-разностные аппроксимации входящих в уравнения производных по всем переменным. В ряде случаев уравнение с частными производными удобно привести к системе обыкновенных дифференциальных уравнений, в которых оставлены производные искомой функции лишь по одной переменной.

Такой способ можно использовать и для решения уравнения Лапласа (2.89). Пусть требуется решить для него задачу Дирихле в прямоугольнике ABCD(рис. 2.29). Разобьем прямоугольник на полосы с помощью прямых, параллельных оси х. Для определенности проведем три отрезка l1, l2, l3, которые разделят прямоугольник на четыре полосы постоянной ширины h. Решение Uзадачи Дирихле приближенно заменим набором функций ui,каждая из которых определена на отрезке li и зависит только от одной переменной х, т.е.ui= ui(х) (i = 1,2,3). На отрезках l0 и l4 значения u0(x) и u4(x) заданы граничными условиями.

Рис. 2.29. К решению задачи Дирихле в прямоугольнике ABCD

Построим разностную схему для определения значений функций u(х). Аппроксимируя в уравнении (2.89) вторую производную по у с помощью отношения конечных разностей, получаем

(2.96)

Таким образом, решение задачи Дирихле (2.89), (2.90) сводятся к решению краевой задачи для системы обыкновенных дифференциальных уравнений (2.96) относительно значений искомой функции вдоль прямых l1, l2, l3. В этом состоит метод прямых. Граничные условия для уравнений (2.96) при х = а, х = bможно получить из уравнений

Направление дискретизации у обычно легко выбрать в тех случаях, когда заранее известен характер поведения искомой функции, это направление должно соответствовать направлению наибольшей гладкости функции.

Метод прямых широко используют для решения нестационарных задач. Например, если имеются две независимые переменные х, t, а искомый параметр является гладкой функцией переменной х, то дискретизацию вводят по этой переменной. Тогда исходную задачу заменяют задачей Коши для системы обыкновенных дифференциальных уравнений вида: