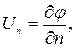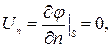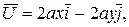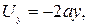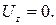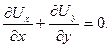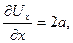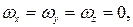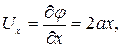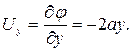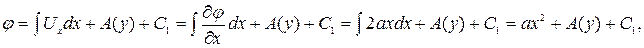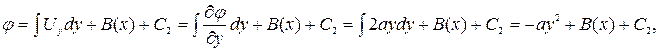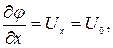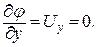Уравнение лапласа для потенциального поля

Уравнения Лапласа для потенциала скорости

Естественно, что при решении задач гидромеханики возникает необходимость найти функцию потенциала скорости φ(x¸y¸z), если это принципиально возможно. Для этого необходимо иметь уравнение, решив которое, возможно найти потенциал скорости. Для получения этого уравнения вспомним, что согласно уравнению неразрывности в каждой точке потока несжимаемой жидкости выполняется

(9.8)

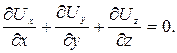
Подставляя в (9.8) выражения для U_x, U_y, U_z из (9.7), получим (в декартовых координатах)

(9.9)

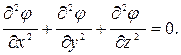
Это уравнение называется уравнением Лапласа. Таким образом, функция φ(x¸y¸z) удовлетворяет уравнению Лапласа. В случае двумерного (в плоскости XOY) течения несжимаемой жидкости уравнение (9.9) принимает вид

(9.10)

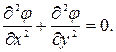
Уравнение (9.9) представляет собой линейное однородное уравнение в частных производных второго порядка с постоянными коэффициентами; этому уравнению должен удовлетворять потенциал скорости любого потенциального течения. Чтобы найти потенциал φ(x¸y¸z) для конкретного потока, необходимо задать границы течения и условия на них. Одним из физически очевидных условий на границе тела (или на границе потока) является непроницаемость этих границ для жидкости, т.е. нормальная составляющая скорости на границе равна нулю. Составляющая скорости по нормали равна

а само условие на границе имеет вид

Именно видом границы и определяется функция φ(x¸y¸z). Решив уравнение Лапласа с заданными граничными условиями и определив функцию φ(x¸y¸z), проекции скорости U_x, U_y, U_z находят простым дифференцированием.

При решении задач, связанных с потенциальными течениями, может быть применён следующий алгоритм:

1. Задаётся граница (на плоскости – кривые или ломаные линии) области течения.

2. Определяются условия на границе для функции потенциала скорости φ(x¸y¸z).

3. Находится решение уравнения Лапласа для потенциала скорости φ(x¸y¸z), удовлетворяющее всем условиям на заданной границе.

В дальнейшем, зная U_x, U_y,U_z , возможно определить величину и направление вектора скорости в любой точке потока.

Задача 9.3.Можно ли рассматривать функцию 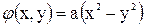в качестве потенциала скорости некоторого плоского течения несжимаемой жидкости (a-постоянная, имеющая размерность )?

Задача 9.4. Вектор скорости плоского потока задан в общем виде так

где a – постоянная, имеющая размерность 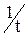. Возможно ли такое течение? Является ли оно потенциальным? Если ответы положительны, найти потенциал скорости φ(x¸y).

Решение. Если составляющие скорости заданного течения

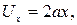
удовлетворяют уравнению неразрывности, которое должно выполняться в каждой точке, то существование такого течения принципиально возможно. Уравнение неразрывности для плоского течения имеет вид

В данном случае частные производные равны

и уравнение неразрывности принимает вид 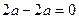, т.е. ответ на первый вопрос положительный и течение с заданным вектором скорости существует. Для проверки, является ли течение потенциальным, необходимо найти величины ω_x, ω_y_, ω_z , вычислив определитель (9.3). Подставляя в (9.5) составляющие скорости из условия задачи, получим

т.е. заданное течение потенциальное и имеет смысл искать функцию потенциала скорости φ(x¸y). По определению из (9.7)

Из этих равенств потенциал φ(x¸y) определяется интегрированием

где A(y), B(x) – произвольные функции; С₁, С₂ – произвольные постоянные.

Подставляя значения φ(x¸y) в уравнение Лапласа (9.10), окончательно имеем

(A(y)=B(x)=0).

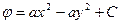
Пример 9.1. Рассмотрим простейший пример потенциального потока — плоский поток жидкости течёт равномерно и прямолинейно вдоль оси X со скоростью U₀, рис. 9.1.

Очевидно, что проекции скорости следующие

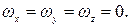
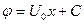
В данном случае движение потенциальное, так как Уравнение Лапласа удовлетворяется. Из выражений для проекций скорости следует, что потенциал φ(x¸y) зависит только от x, поэтому .

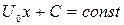
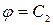
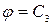
Линии равного потенциала (эквипотенциальные линии) можно найти из выражения или .Эти линии показаны отрезками , , на рис. 9.2.

Уравнение Пуассона и Лапласа

В случае потенциального поля напряженность поля Е может быть выражена через градиент потенциала. При этом приходим к выражению

содержащему двойную дифференциальную операцию: дивергенцию от градиента. При использовании декартовой системы координат легко записать эту операцию через соответствующие производные. Действительно, представляя в формулу (1) составляющие grad φ как:

Операция div grad носит название лапласиана и обозначается знаком Δ. Используя оператор набла, рассматриваемую операцию можно представить как наблу квадрат, таким образом:

В случае декартовых координат и в применении к скалярной функции можно всегда считать операции ∇ 2 и Δ тождественными.

Уравнение (1) является основным уравнением потенциального электрического поля и носит название уравнения Пуассона.

В области поля, где заряды отсутствуют (где ρ = 0), уравнение (1) упрощается, так как в его правой части оказывается нуль. В последнем случае уравнение называют уравнением Лапласа.

и было названо дифференциальным уравнением электрического потенциального поля.

Рассмотрим несколько примеров.

Пример 1

В некоторой области поля потенциал изменяется по закону:

Содержится ли в этой области объемный заряд и чему он равен?

Решение

Путем прямого дифференцирования найдем:

Уравнение Лапласа удовлетворяется (объемный заряд равен нулю).

Пример 2

То же, что и в предыдущем примере, но описанное следующим уравнением:

Решение

Очевидно, что правая часть данного равенства в общем случае не равна нулю.

Примечание к примерам 1 и 2. Из рассмотрения встретившихся видов произведений можно сделать более общий вывод:

всегда удовлетворяет уравнению Лапласа (первый множитель в формуле (5) cos или sin, а второй ch или sh).

Уравнение Пуассона и уравнение Лапласа

Уравнение Пуассона и уравнение Лапласа. Уравнение Пуассона и уравнение Лапласа являются основными уравнениями статического электричества. Они следуют теореме Гаусса в дифференциальной форме.

Действительно, E = -grad cf. В то же время, согласно теореме Гаусса, div £ = (13.21) e. Подставим E из (13.6) в (13.21). div E = div (-grad ” dv2′ de (13.29) y2 ^

не выводится в цилиндрической системе (13.30) Людмила Фирмаль

сферическая система координат V2 ± Д / ^ 2 ^ _ \ _ |! A / Sino ^ \ 1? Ф. (13.31) R2 dR \ dR) 1 /? 2sinOдЭ \ дБ) 1 sin2 0 yes2 ‘ * * Уравнение Пуассона зависит от второй производной от φ в любой точке электрического поля и объемной плотности свободного заряда в этой точке электрического поля.

В то же время потенциал φ в любой точке электрического поля, конечно, зависит не только от величины свободного заряда, но и от всех зарядов, создающих электрическое поле, уравнение Лапласа (1780) описывает потенциальное поле небесной механики

Сначала был применен, а затем используется для описания электрического поля. Уравнение Пуассона применяется для изучения электрических потенциальных полей (электрических и магнитных полей) с 1820 года.

Подумайте о том, как вообще можно записать решение уравнения Пуассона. Объем V имеет объем (р), поверхность (о) и линейные (т) заряды. Эти заряды выражаются в виде набора точечных зарядов pdV, ®ds, rd /. dV — элемент объема, ds — элемент заряженной поверхности, а

dl — элемент длины заряженной оси. Людмила Фирмаль

Согласно уравнению (13.19), составляющая потенциала dq в точке пространства p от pdV равна p dV — 4 l? Потенциальные компоненты поверхностного заряда R и линейного заряда определяются аналогично, рассматривая их как точечные заряды: o ds td / 4 rciR 4neR полное значение (p — сумма потенциальных компонентов всех зарядов в поле (интеграл )

Определяется как: f pdV | 1 f ods .1 C Td / JR4шJR 4ne JR 1

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

источники:

http://elenergi.ru/uravneniya-puassona-i-laplasa-dlya-potencialnogo-polya.html

http://lfirmal.com/uravnenie-puassona-i-uravnenie-laplasa/