iSopromat.ru
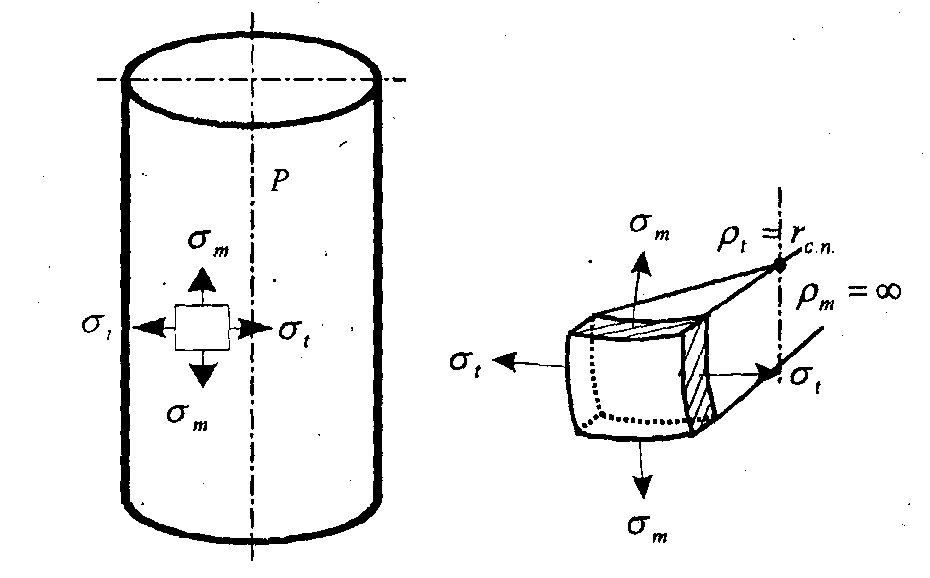
Оболочки, имеющие форму тел вращения (рис. 11.1), стенки которых тонки ( t ≤ 0,1D0 ), не имеют резких переходов и изломов при действии осесимметричных нагрузок (например, давления жидкости или газа), попадают под класс тонкостенных сосудов и могут быть рассчитаны по безмоментной теории.
Связь между меридиональными σm и кольцевыми σt нормальными напряжениями (рис. 11.1) описывается уравнением Лапласа:
где ρm и ρt – радиусы кривизны серединной поверхности меридионального и кольцевого сечений на уровне рассматриваемой точки;
р – интенсивность внутреннего давления.
Для определения σm обычно используется зависимость
где Q – вес части сосуда и жидкости ниже рассматриваемого сечения.
Уравнения (11.1) и (11.2) позволяют найти величины σm и σt в каждой точке сосуда.
Рассмотрим частные случаи:
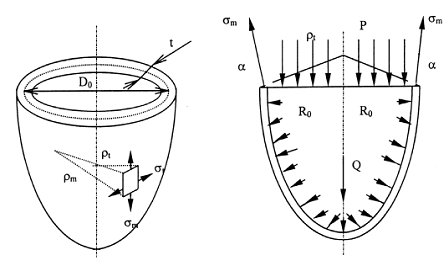
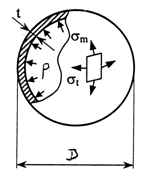
Сферическая оболочка
Сферический сосуд под действием внутреннего давления газа (рис.11.2).
Благодаря симметричности сосуда
Из уравнения (11.1) находим
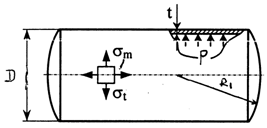
Цилиндрическая оболочка
Цилиндрический сосуд под действием внутреннего давления газа (рис. 11.3).
Для цилиндрической части сосуда имеем:
Из уравнения (11.1) находим
Из уравнения (11.2), полагая cosα = 1, Q = 0,
Напряжения в днищах определяем, как в сферическом сосуде:
Напряжения в стенках труб
Напряжения в стенке трубы определяются аналогично, как для цилиндрической части тонкостенного сосуда.
Сравнение (11.4) и (11.5) показывает, что σt = 2σm , т.е. напряжения, растягивающие стенки цилиндрической части сосуда, по окружности в 2 раза больше напряжений вдоль образующей. Поэтому разрушение котлов, труб обычно происходит от кольцевых напряжений вдоль образующей.
Третье главное напряжение, перпендикулярное к поверхности сосуда со стороны, где действует давление,
с противоположной стороны, σ3 =0 .
В тонкостенных оболочках обычно величины σm и σt намного больше, чем интенсивность внутреннего давления р, и поэтому величиной σ3 можно пренебречь, т.е. считать равной нулю.
Так как в любой точке тонкостенного сосуда имеет место сложное напряженное состояние, для расчета на прочность в зависимости от материала следует пользоваться соответствующей гипотезой прочности
Для рассматриваемой задачи при неучете σ3 эквивалентные напряжения по третьей гипотезе прочности и по гипотезе Мора одинаковы, т.е.
а по энергетической теории
Если тонкостенный сосуд имеет резкие переломы в очертании (например, примыкание днищ к цилиндрической части), а также в местах закрепления, приложения сосредоточенных сил, установки патрубков, фланцев, у краев оболочки возникает изгиб. Зоны, прилегающие к таким местам, должны рассчитываться по моментной теории.
Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах
Тонкостенная осесимметричная оболочка
Тонкостенной осесимметричной называется оболочка, имеющая форму тела вращения толщина, которой мала по сравнению с радиусами кривизны ее поверхности (рис.1).
При расчете тонкостенных оболочек все нагрузки, действующие на них, прикладывают к срединной поверхности оболочки.
К тонким оболочкам могут быть отнесены такие часто встречающиеся элементы конструкций как резервуары, цистерны, газовые баллоны, корпуса аппаратов химических агрегатов и др.
При расчете таких элементов конструкций используется безмоментная теория оболочек, основные положения которой заключаются в следующем:
1. нагрузки, действующие на поверхности оболочки, могут считаться перпендикулярными им и симметричными относительно оси вращения оболочки;
2. вследствие малой толщины оболочки сопротивление изгибу отсутствует (изгибающий момент не возникает);
3. напряжения по толщине стенки оболочки распределены равномерно.
Из оболочки, изображенной на рис.1 выделим двумя меридиональными плоскостями nn1n2 и nn3n2, (т.е. плоскостями проходящими через ось симметрии оболочки), с углом dφ между ними и двумя плоскостями, перпендикулярными оси симметрии оболочки BC и AD, элементABCD.
Радиусы кривизны O2A и O2B элемента ABCD в меридиональной плоскости обозначим через R2, а радиусы кривизны O1B и O1C в плоскости, перпендикулярной меридиану, обозначим через R1. Нормальные напряжения, действующие по боковым граням AB и CD, соприкасающимся с меридиональными плоскостями, называются окружными напряжениями σt. Нормальные напряжения, действующие по боковым граням BС и AD, называются меридиональными напряжениями σs. Кроме напряжений σs и σt. на элемент оболочки действует нагрузка в виде давления q, перпендикулярного поверхности ABCD.
Рис.1
Основным уравнением безмоментной теории оболочек является уравнение Лапласа, которое имеет следующий вид
где δ — толщина оболочки.
Прежде чем перейдем к рассмотрению различных вариантов определения напряжений в оболочках остановимся на некоторых различиях, вызванных наличием газа или жидкости внутри оболочки.
В случае газового давления величина давления q постоянная во всех точках поверхности оболочки. Для резервуаров, наполненных жидкостью, значение q по их высоте переменно.
Для случая наполнения резервуара жидкостью необходимо учитывать, что если на какую-либо поверхность действует давление жидкости, то вертикальные составляющие сил давления равны весу жидкости в объеме, расположенном над поверхностью. Поэтому давление жидкости в различных сечениях оболочки будет различным, в отличие от давления газа.
Определим напряжения в сферических и цилиндрических оболочках т.к. они наиболее часто используются в промышленности.
Сферическая оболочка
Отсечем часть сферической оболочки нормальным коническим сечением с углом 2φ при вершине и рассмотрим равновесие этой части оболочки вместе с заключенной в ней жидкостью с удельным весом γ. Сферическую часть отделим от основной оболочки плоскостью, перпендикулярной оси симметрии.
Рис.2
На рис.2 изображена расчетная схема сферической оболочки радиусом Rs. Высота отсеченной поверхности 
где 
Уравнение равновесия отсеченной части может быть записано, как сумма проекций всех сил на вертикальную ось
В данном уравнении величина G – вес жидкости, заполняющей отсеченную часть сферической оболочки (см. рис.8.2).
где 
Путем интегрирования объем сферического сегмента может быть определен по формуле
После подстановки уравнения (8.5) в выражение (8.4), и затем, в (8.3), получим конечное уравнение равновесия для сферической части сегмента
Из этого уравнения можно определить величину меридионального напряжения 

Цилиндрическая оболочка
Рассмотрим цилиндрическую оболочку радиусом 
Рис.3
В данном случае цилиндрическая часть отделена от остальной части оболочки сечением, перпендикулярным оси симметрии.
Уравнение равновесия отсеченной части может быть получено, как сумма проекций всех сил на вертикальную ось.
где 
Объем цилиндра с высотой x и радиусом 
С учетом этого уравнение равновесия принимает вид
В этом уравнении, также как и в предыдущем случае, одна неизвестная
Для случая цилиндрической оболочки при подстановке в уравнение Лапласа необходимо учесть, что величина 

Коническая оболочка
Отсечем часть конической оболочки нормальным коническим сечением с углом 2φ при вершине и рассмотрим равновесие отсеченной части.
Рис.4
Как видно из рис.4 φ = π/2 — α.
Уравнение равновесия отсеченной части оболочки будет иметь вид
где 
С учетом (8.11), выражение (8.10) имеет следующий вид
Из этого уравнения можно рассчитать величину меридионального напряжения 

Возможно отделение сечением не нижней, а верхней части оболочки с последующей записью уравнения равновесия. Это делается для того, чтобы при составлении условий равновесия отсеченного элемента крепление оболочки не попадало в схему отсеченной части. В подобных вариантах во всех рассмотренных случаях изменится знак силы G, т.к. в этом случае ее направление будет совпадать с направлением вертикальной составляющей напряжения 
В этом случае, при расчете величины G, в качестве объема будет браться объем отсеченной верхней части 

В случае, если жидкость находится в сосуде под давлением P, то при расчете величины q добавляется величина давления P. Формула (8.2) будет иметь следующий вид
В некоторых задачах отсеченная часть представляет собой не какой-то один элемент, а два или более состыкованных элемента. При этом вид уравнений равновесия остается неизменным, а изменяется только величина объема верхней или нижней части сосуда, однако, если известны зависимости, определяющие объемы элементов, то найти суммарный объем не представляет затруднения.
На рис.5, а показана схема оболочки вращения, состоящей из сферической, цилиндрической и конической оболочек. Крепление оболочки располагается на уровне стыка сферической и цилиндрической оболочек. Сосуд наполнен жидкостью, находящейся под давлением Р.
На рис.5, б показан пример построения эпюр напряжения. В левой половине оболочки расположена эпюра 

Рис.5
Полученные построения справедливы для участков, находящихся на некотором удалении от линии закрепления оболочки и точек сопряжения сфера-цилиндр и цилиндр-конус. В точках сопряжения возникают эффекты, которые не могут быть учтены теорией безмоментногонапряженного состояния. Все это также относится и к точкам, непосредственно примыкающим к вершине конуса.
Толстостенный цилиндр
Толстостенным называется такой цилиндр, для которого отношение толщины стенки к внутреннему диаметру не менее 1/20.
Задача о расчете толстостенного цилиндра решается с учетом равномерно распределенного наружного давления 

Нормальные напряжения 
Нормальные напряжения 

Рис.6
В поперечных сечениях цилиндра касательные напряжения также предполагаются равными нулю, однако, возможно существование нормальных осевых напряжений 

Основными уравнениями для расчета напряжений в толстостенных цилиндрах являются формулы Ламе:
При действии на цилиндр только наружного или внутреннего давления знаки эпюр 



Рис.7 Рис.8
При нагружении внутренним давлением эпюры изменения радиального окружного напряжения показаны на рис.8. Окружное напряжение является расширяющим, а радиальное сжимающим.
Анализ формул Ламе показывает, что увеличение толщины не может во всех случаях обеспечить необходимой прочности цилиндра. Поэтому для сосудов высокого давления необходимо искать какие-то другие конструктивные решения. Одним из таких решений является создание составных, соединенных с натягом, цилиндров. Этот прием используется как в технике высоких давлений, так и в артиллерийской практике для упрочнения стволов мощных орудий.
В результате натяга в трубах возникают нормальные напряжения, которые частично компенсируют напряжения в трубе от действия высокого давления.
Составные цилиндры. Автофретирование. Общие положения
Из формул (8.14) и (8.15) следует, что при действии только внутреннего давления напряжения 


В остальных точках напряжения 
Наибольшее значение 
Чтобы соединить цилиндры наружный цилиндр обычно нагревают, он расширяется и появляется возможность одеть его на внутренний цилиндр. Возможно такое охлаждение внутреннего цилиндра в жидком азоте или запрессовка цилиндров друг в друга. После сборки выравнивается температура, наружный цилиндр плотно охватывает внутренний и получается надежное соединение.
В результате натяга в трубах возникают начальные напряжения, причем, чем больше величина натяга, тем больше начальные напряжения.
Способ уменьшения напряжений 
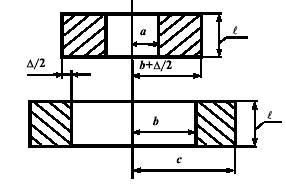
Обозначим через b и c радиусы наружного цилиндра, через a и b+∆/2 радиусы внутреннего цилиндра, а ∆ — натяг (см. рис.9).
Рис.9
При одинаковой длине соединенных цилиндров контактное давление pk равномерно распределено по посадочной поверхности.
Подставив в формулы(8.14) и (8.15) параметры, характеризующие напряжения в наружном цилиндре получим
Аналогично можно определить напряжения, возникающие на посадочной поверхности внутреннего цилиндра
Если внутренний и наружный цилиндры изготовлены из одного и того же материала, то контактное давление pk определяется зависимостью
где Е – модуль упругости материала внутреннего и наружного цилиндров.
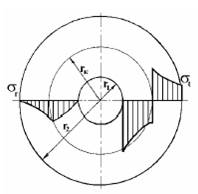
За счет натяга в составном цилиндре возникают начальные напряжения, характер изменения которых по наружному сечению показан на рис.10.
Рис.10Рис.11
При приложении внутреннего рабочего давления на начальные напряжения накладываются рабочие напряжения (показываются на рис.11 пунктиром). Суммарные напряжения показаны на рис.11.
В точках, расположенных на внутренней поверхности составного цилиндра, суммарное окружное напряжение получается меньше, чем в тех же точках целого цилиндра.
Оптимальное значение натяга можно определить из условия равнопрочности внутреннего и наружного цилиндров, оптимальное значение радиуса контактной поверхности – из условия наибольшего снижения эквивалентного напряжения в опасной точке.
В соответствии с этим оптимальный радиус контактной поверхности:
Натяг соответствующий этому радиусу и внутреннему давлению pв:
Необходимо отметить, что детали, предназначенные для соединения с натягом, должны изготавливаться с большой точностью, т.к. даже небольшое отклонение от номинальной величины натяга может привести к снижению прочности соединения.
В технике высоких давлений, кроме посадки, применяется так называемое автофретирование, которое заключается в предварительной нагрузке цилиндра внутренним давлением, больше рабочего, с таким расчетом, чтобы во внутренних слоях цилиндра возникали пластические деформации. После снятия давления во внешних слоях цилиндра сохраняются упругие напряжения растяжения, а во внутренних слоях возникают деформации сжатия (см. рис.12).
В дальнейшем при нагрузке цилиндра давлением остаточные напряжения суммируются с рабочим так, что во внутренних слоях имеет место чистая разгрузка. Материал цилиндра не получает пластических деформаций, если только рабочее давление не превышает давление предварительного обжатия.
Рис.12
Постановка задачи.
В ходе работы необходимо провести расчет на прочность оболочки двигателя .Для этого работа разделяется на несколько этапов:
1. Построение 3D-модели в SolidWorks.
• Заготовка 3-d модели.
• Скругление элементов 3-d модели.
• Сохранение модели в формате, совместимости с ANSYS.
2. Работа с моделью в ANSYS.
• Импортирование сохраненного файла.
• Задание материала конструкции
• Конечно-элементное разбиение модели
• Приложение экспериментальных нагрузок
3. Обсуждение результатов.
Создание детали.
Открываем программу SolidWorks, выбираем вид спереди, вставляем эскиз и строим нашу модель. Чтобы получить нашу деталь, выбираем команду «Повернутая бобышка/основание», указываем ось вращения и наш эскиз и крутим на 360 градусов (Рис.13)
Рис.13 Заготовка 3-d модели.
В получившейся заготовке делаем скругление элементов заготовки , с помощью команды «Скругление» (Рис.14)
Рис.14 Скругление элементов заготовки.
Решение задачи в ANSYS
4.1. Создание материала
Открываем программу ANSYS Workbench. При помощи мышки вытаскиваем окно Static Structural. Это окно содержит пункты: библиотека, геометрия, разбиение, результаты и др.
Рис.14. Окно Static Structural
В этом окне двойным щелчком мыши по Engineering Data открываем библиотеку материалов и выбираем материал Aluminum Alloy.
Рис. 15. Библиотека материалов
Загружаем нашу модель построенную в Solid Works в ANSYS Workbench, для этого правой клавишей нажимаем в окне Static Structural на Geometry.
Рис. 16. Выбор геометрии
После открываем нашу геометрию, нажимаем на Generate и получаем нашу модель.
Рис. 17. Модель оболочки двигателя после импорта в ANSYS
4.2. Приложение нагрузок и результаты
Чтобы получить более точные результаты расчетов, разбиваем модель изолятора на конечные элементы. Для этого открываем пункт Model. Затем в дереве построений нажимаем правой клавишей на Mesh, затем на Generate Mesh.
Для того чтобы задать размер разбиения в команде Mesh Control выбираем Sizing. Параметры Sizing позволяют изменить плотность сетки отдельной детали, увеличить или уменьшить размер элементов относительно параметров, заданных глобально. В результате всех операций получаем разбиение оболочки двигателя .
Рис. 18.Конечная–элементная сетка.
Качество сетки хорошее это обусловлено геометрией модели и методом разбиения.
4.3 Нахождение максимальных деформаций
Данный расчет будет проведен для материала алюминий . В дереве построения выбираем вкладку Geometry и выбираем материал Aluminum Alloy. Следующим шагом является создание закреплений.
Командой Fixed Support задаем жесткую заделку. Модель становится закрепленной и становится возможным приложение нагрузки.
В дереве построения выбираем команду Static Structural→ Loads→ Force.
Нагрузку, равную 50 МПа., мы будем прикладывать к верхней части оболочки. Выбираем в дереве построения вкладку Solution и выбираем пункт Deformation→Total Deformation. Выбираем нашу модель и нажимаем команду Solve для расчетов. И получаем диаграмму деформаций элерона (рис.19).
Рис.19. Деформация элемента оболочки
Диаграмма показывает максимальные деформации красным цветов, на оболочке они возникают в самой верхней части . Максимальная деформация равна 0,28 мм.
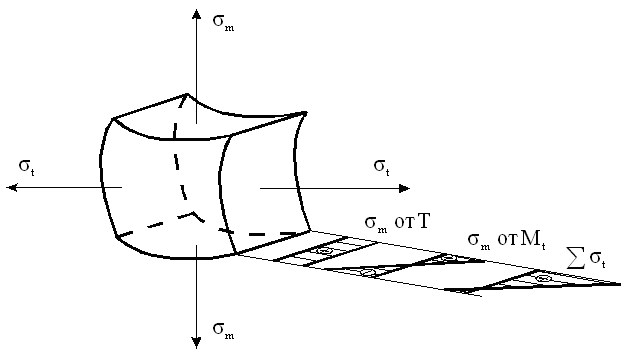
Напряженное состояние материала упругих осесимметричных оболочек вращения
Тонкостенные сосуды и аппараты
Сосуды и аппараты, применяемые в газовой, нефтеперерабатывающей, химической, нефтехимической, пищевой, и смежных отраслях промышленности отличаются друг от друга конструктивным исполнением, материалом, размерами 
Тонкостенными принято считать сосуды и аппараты, если толщина их стенки S не превышает 10% внутреннего диаметра Dв. Такие сосуды и аппараты эксплуатируются обычно при давлении не более 10 МПа.
По ГОСТу 14249-89 тонкостенным называется сосуд, если:
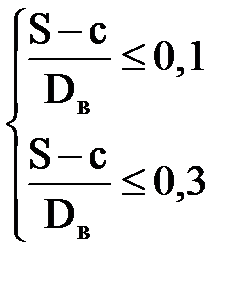 , , | для обечаек и труб при Dв ³ 200 мм | |||||
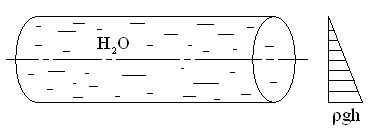
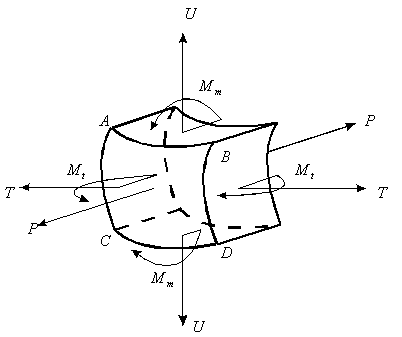
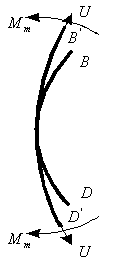
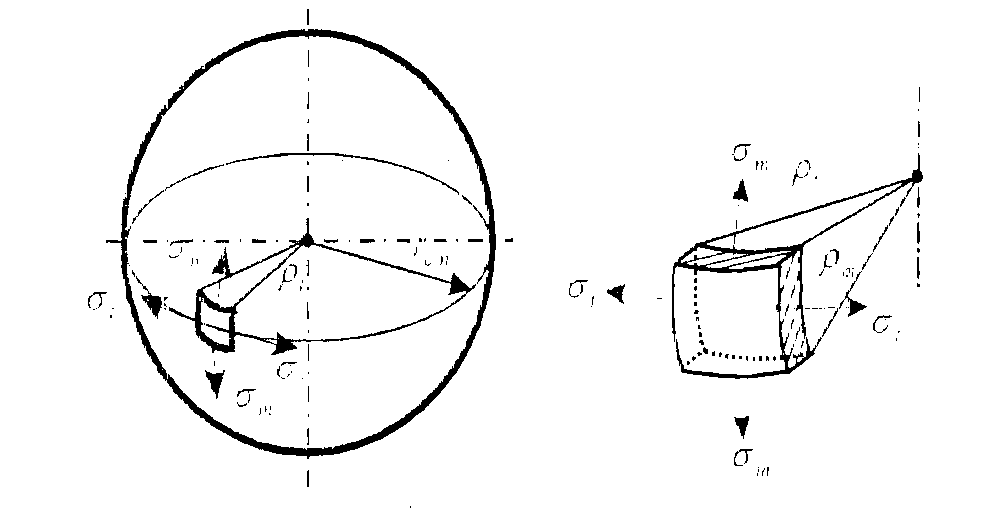
| для обечаек и труб при Dв Рисунок 3.1.3 – Эпюра распределения гидростатического давления для горизонтального аппарата внутренней поверхностей оболочки Меридианаминазываются кривые, образованные пересечением срединной поверхности плоскостями, проходящими через ось симметрии оболочки (рисунок 3.1.4). Рисунок 3.1.4 – Срединная поверхность Параллелями(параллельными кругами или кольцевыми сечениями) называются окружности, образованные пересечением срединной поверхности плоскостью, перпендикулярной оси оболочки. Полюсом оболочки называется точка пересечения срединной поверхности с осью (рисунок 3.1.5). Рисунок 3.1.5 – Основные параметры оболочки Параметры rm, rt называются радиусами кривизны соответственно меридиана и параллельного круга. Напряженное состояние материала упругих осесимметричных оболочек вращения При расчете оболочек вращения обычно определяют напряжения от действия внутреннего давления и толщину стенки. При этом рассматривают бесконечно малый элемент “D”, выделенный из оболочки двумя меридиональными и двумя кольцевыми сечениями (рисунок 3.1.6). Рисунок 3.1.6 – Элемент оболочки rm – радиус кривизны меридиана; rt – радиус кривизны параллельного круга. Как известно из курса сопротивление материалов, в самом общем случае от действия внешних нагрузок по каждой из граней могут действовать шесть внутренних силовых факторов (ВСФ): – продольное (нормальное) усилие (сила) Nz; – изгибающие Mx, My и крутящий Mz моменты, от которых возникают нормальные s (от Mx, My, Nz ) и касательные t (от Q x, Qy, Mz) напряжения. На рисунке 3.1.7 показаны внутренние силовые факторы только по одному из сечений – меридиональному, аналогично можно было бы изобразить внутренние силовые факторы и по остальным трем граням. Какие внутренние силовые факторы возникают в оболочке под действием внутреннего давления Рвнутр? Для решения этой задачи рассмотрим пример – воздушный шарик, находящийся под действием газового давления. Рисунок 3.1.7 – Внутренние силовые факторы, действующие на выделенный T, U– тангенциальные и меридиональные растягивающие усилия; Mt, Mm – тангенциальный и меридиональный изгибающий моменты; P – усилие от давления. Изобразим деформации стенки сферы (рисунке 3.1.8).
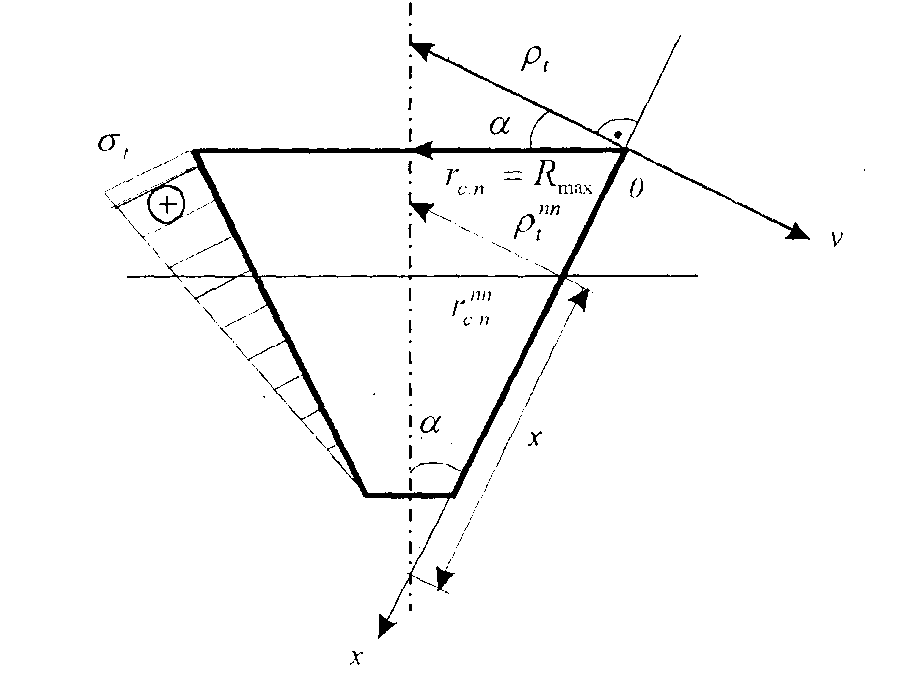
Рисунок 3.1.8 – Деформации сферической оболочки Допустим, надули шарик до давления P1 и он принял определенный размер, характеризующийся длиной окружности поперечного сечения. Надуваем шарик до давления P2 > Р1, размеры шарика увеличиваются и, соответственно, изменяются размеры дуги AB. Совместим эти дуги до деформации и после (рисунок 3.1.9). Рисунок 3.1.9 – Схема совмещения дуг AB и A’B’ Из рисунка видно, что дуги не совпадут, так как, во-первых, одна дуга длиннее другой, т.е. на нее должны действовать растягивающие усилия, в данном случае тангенциальные – T , а во-вторых, различна их кривизна. Изменить свою кривизну дуга может только под действием изгибающих моментов. Для рассматриваемого случая это – Мt. Если шарик повернуть на 90°, то параллельный круг превратится в меридиан. Для дуги BD будут происходить аналогичные изменения, т.е. на эту дугу будут действовать меридиональные растягивающие усилия U и меридиональный изгибающий момент Mm (рис.унок 3.1.10). Таким образом, в оболочках под действием внутреннего давления возникают усилия U и T и изгибающие моменты Мt, Мm. Рисунок 3.1.10 – Схема совмещения дуг BD и B’D’ Доказано, что в случае, когда вдоль меридиана не будет резких изменений внешней нагрузки, толщины оболочки и ее радиусов кривизны, то можно принять, что оболочка не подвергается изгибу, т.е. изгибающие моменты и поперечная сила равны нулю (Мx = Мy = Оy = 0), благодаря же симметрии формы и нагрузки оболочки действие крутящих моментов Мz и поперечной силы Оx на всех гранях исключено и тогда касательные напряжения отсутствуют. Таким образом, по граням действуют только нормальные усилия N; будем называть их соответственно меридиональными и обозначать N = U (по меридиональным сечениям АВ и СД) и тангенциальными (кольцевыми) N = Т (по граням АС и ВД). От них возникают нормальные напряжения, соответственно — меридиональные sm и тангенциальные st (рисунок 3.1.11). Рисунок 3.1.11 – Напряженное состояние и эпюры распределения тангенциальных напряжений по толщине стенки Кроме этого на грань АВСД действует внешняя нагрузка Р. (В данном примере это внутренне избыточное давление). От этой нагрузки возникает, так называемое, радиальное напряжение, направленное вдоль радиуса оболочки и равное по величине давлению, т. е. sr = Р. Так как для тонкостенных оболочек давление обычно меньше 10 МПа, то радиальное напряжение также не больше этого значения, и соответственно, значительно меньше допускаемых напряжений. Поэтому для тонкостенных оболочек обычно пренебрегают величиной радиальных напряжений и принимают их равными нулю. При расчете тонкостенных оболочек считают, что кольцевые и меридиональные напряжения постоянны по толщине оболочки, т.е. пренебрегают их изменением (рисунок 3.1.11), как это наблюдается для толстостенных аппаратов. Таким образом, можно принять, что напряженное состояние тонкостенных оболочек – плоское (двухосное). Основанная на этих предположениях теория, не учитывающая действие изгибающих моментов, а принимающая во внимание только продольные силы U и Т, называетсябезмоментной илимембранной теорией расчета оболочек, в отличие отмоментной теории. 3.1.3 Безмоментная теория расчета оболочек Определение напряжений Основным исходным уравнением безмоментной теории для расчета на прочность осесимметричных оболочек вращения, нагруженных внутренним избыточным давлением, является уравнение Лапласа. Для его нахождения рассмотрим равновесие выделенного элемента “Э” под действием равномерно распределенного внутреннего давления. Приложим внешние нагрузки и покажем внутренние силовые факторы, как изображено на рисунке 3.1.12. Рисунок 3.1.12 – Выделенный элемент оболочки, находящийся в равновесии под действием равномерно распределенного давления Рассмотрим условие равновесия всех сил на ось Y. Для наглядности рассмотрим этот элемент с двух видов (рисунок 3.1.12). Сумма всех сил, действующих вдоль оси Y, равна нулю, т.е. Рисунок 3.1.12 – Элемент оболочки. Вид сверху Как было сказано ранее на элемент действуют напряжение sm на гранях АС и ВD, а напряжение st на гранях АВ и СD. Кроме того, внешние силы, нормальная составляющая которых, относится к единице площади, есть Р (внутреннее давление). Составим уравнение равновесия в проекциях на нормаль (ось у), проведенную в середине элемента. На грани АВСD, площадь которой есть S*dlm, действует напряжение st. Таким образом, сила, действующая на указанной грани, равна Эта сила составляет с осью Y угол, равный Рассматривая совершенно аналогичные силы, действующие на грани АС и ВD, найдем, что проекция каждой из них на нормаль равна Наконец, составляющая внешней силы, направленная вдоль оси Y (по нормали), равна Находя сумму проекций на нормаль всех действующих на элемент сил и приравнивая эту сумму нулю, получим или, если вместо Т, U и P ’ подставить из (3.1.1) значения, выраженные через напряжения и внешнюю нагрузку, уравнение (3.1.4) примет вид В виду малости углов Сократив каждый член данного уравнения на Полученное уравнение носит название уравнение Лапласа. Одного этого уравнения недостаточно для определения напряжений sm и st, т.е. для нахождения этих напряжений к уравнению (3.1.8) нужно добавить еще одно уравнение. Для получения второго уравнения отсечем нормальным коническим сечением часть оболочки и отбросим верхнюю часть. Для оставшегося элемента (так называемой зоны оболочки), показанного на рисунке . составим уравнение равновесия всех сил в направлении оси оболочки Х. Площадь А поверхности поперечного сечения элемента есть кольцо. Поэтому На нее действует меридиональная сила U, от которой возникает напряжение Кроме этого, на выделенный элемент действует осевая равнодействующая Р’ внешних сил,приложенных к отсеченной части. В качестве внешних сил выступает равномерное внутреннее давление Р. Проектируя все силы на ось Х, получим где a – угол между направлением U и осью Х. Доказано, что если на какую-либо поверхность действует равномерно распределенное давление, то независимо от формы поверхности, проекция равнодействующей сил давления, на заданную ось равна произведению давления Р на площадь проекции поверхности А’ на плоскость, перпендикулярную к заданной оси. Следовательно Таким образом, для того чтобы определить проекцию равнодействующих сил давления на ось Х, нужно предварительно спроектировать поверхность на плоскость, перпендикулярную этой оси и определить ее площадь. Для рассматриваемой зоны проекция ее поверхности на плоскость, перпендикулярную оси Х, представляет собой окружность и площадь, соответственно, равна Подставляя значение Р’ в уравнение (3.1.13), получим Это уравнение называется уравнением равновесия зоны или просто уравнением зоны. Из этого уравнения находится меридиональное напряжение sm. Таким образом, по безмоментной теории напряжения sm и st в оболочке определяются из уравнений равновесия. Мембранная теория дает следующие значения напряжений для основных геометрических форм оболочек: – сферический сосуд (шаровая оболочка, полушаровое днище) (рисунок 3.1.13), нагруженный равномерно распределенным внутренним давлением Р. Для него rt = rm = R , где R – радиус сферы. Рисунок 3.1.13 – Сферическая оболочка, нагруженная внутренним давлением Тогда меридиональное напряжение sm равно кольцевому напряжению st и они определяются по формуле где rсп – радиус срединной поверхности, м. Рисунок 3.1.14 – Применение сферических оболочек для изготовления шаровых емкостей и полусферических днищ – цилиндр с крышками, нагруженный равномерно распределенным давлением Р. (рисунок 3.1.15) Рисунок 3.1.15 – Цилиндрическая обечайка то есть в продольных швах действуют в два раза большие напряжения, чем в поперечных (см. рисунок 3.1.11), и соответственно по этим швам в первую очередь может произойти разрыв при разрушении оболочки. – конус, шарнирно подвешенный по краю со стороны основания, нагруженный равномерно распределенным давлением Р. Кольцевые напряжения в любом сечении конического днища n — n можно найти из уравнения Лапласа. Учитывая, что величина где Из формул (3.1.24) и (3.1.25) вытекает, что максимальная величина кольцевых и меридиональных напряжений будет на краю конуса при r = R, причем при этом кольцевые напряжения (как и для цилиндра) в любом данном сечении в 2 раза больше меридиональных, т.е. У вершины конуса при г = 0 и кольцевые и меридиональные напряжения равны нулю. Пример эпюры тангенциальных напряжений приведен на рисунке 3.1.16. Риcунок 3.1.16 – Коническая оболочка, нагруженная внутренним давлением Те же значения будут справедливы и для усеченного конуса, закрытого днищем. Эти формулы верны в том случае, если угол a источники: http://allrefrs.ru/3-2.html http://poisk-ru.ru/s35821t19.html |

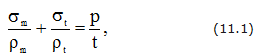
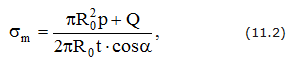

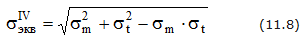

















































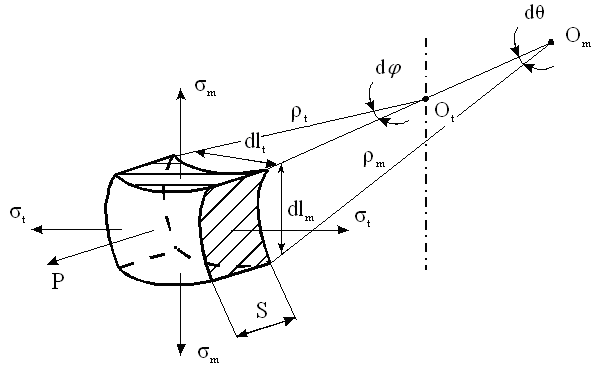
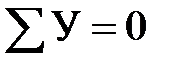
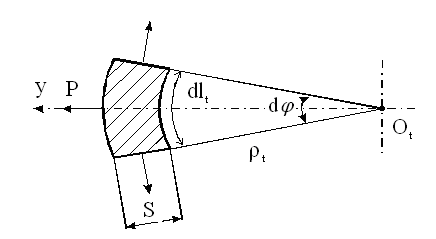
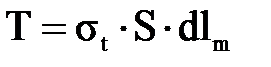 . (3.1.1)
. (3.1.1)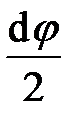 , и направлена в противоположную оси Y сторону, поэтому ее проекция на нормаль равна —
, и направлена в противоположную оси Y сторону, поэтому ее проекция на нормаль равна — 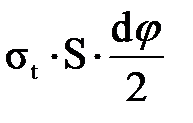 .
. (3.1.2)
(3.1.2)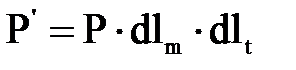 . (3.1.3)
. (3.1.3) , (3.1.4)
, (3.1.4)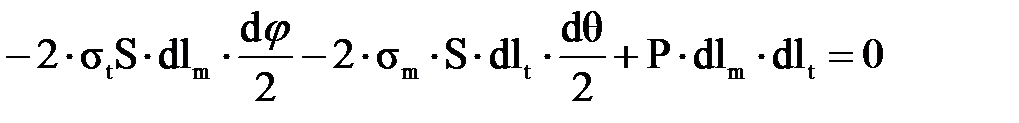 (3.1.5)
(3.1.5)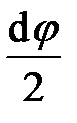 и
и 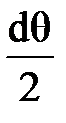 можно записать, что
можно записать, что 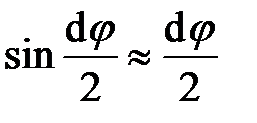 ,
, 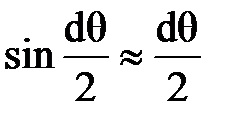 . Кроме того, используя зависимость между длной дуги и радиусом кривизны, получим
. Кроме того, используя зависимость между длной дуги и радиусом кривизны, получим 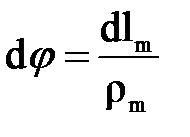 и
и 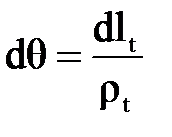 . Подставляя эти значения в уравнение (3.5), имеем
. Подставляя эти значения в уравнение (3.5), имеем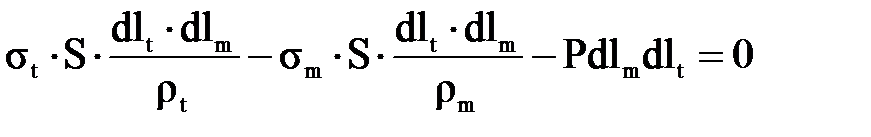 (3.1.6)
(3.1.6)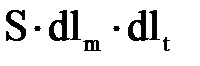 , его можно записать следующим образом
, его можно записать следующим образом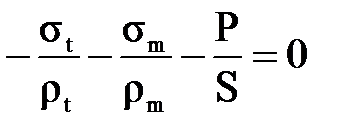 , (3.1.7)
, (3.1.7)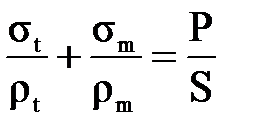 . (3.1.8)
. (3.1.8)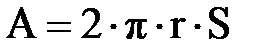 . (3.1.9)
. (3.1.9)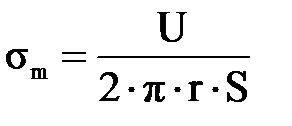 . (3.1.10)
. (3.1.10)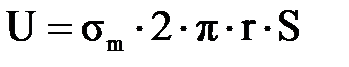 . (3.1.11)
. (3.1.11)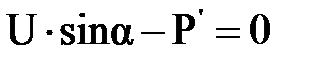 , (3.1.12)
, (3.1.12)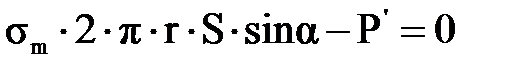 , (3.1.13)
, (3.1.13) . (3.1.14)
. (3.1.14) . (3.1.15)
. (3.1.15)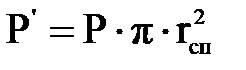 . (3.1.16)
. (3.1.16) (3.1.17)
(3.1.17) . (3.1.18)
. (3.1.18)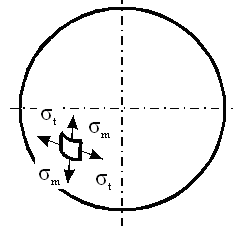
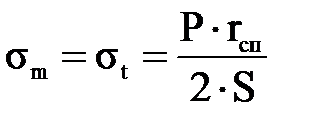 , (3.1.19)
, (3.1.19)
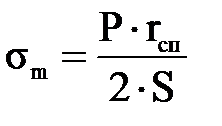 , (3.1.20)
, (3.1.20)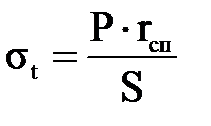 , (3.1.21)
, (3.1.21)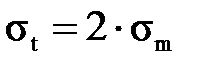 , (3.1.22)
, (3.1.22) , (3.23)
, (3.23)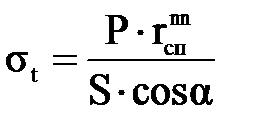 , (3.24)
, (3.24) ,
, 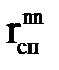 – соответственно радиус кривизны и радиус конуса в сечении n – n. Величину меридиональных напряжений, возникающих в сечении n – n конуса можно определить из уравнения зоны (4), т.е
– соответственно радиус кривизны и радиус конуса в сечении n – n. Величину меридиональных напряжений, возникающих в сечении n – n конуса можно определить из уравнения зоны (4), т.е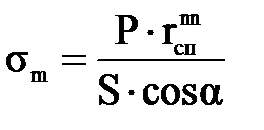 . (3.25)
. (3.25)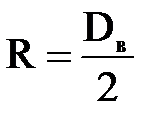 , (3.26)
, (3.26)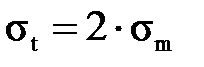 . (3.27)
. (3.27)