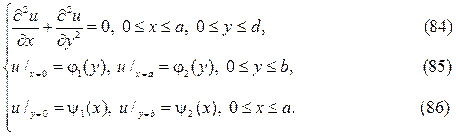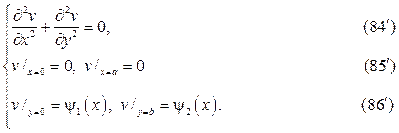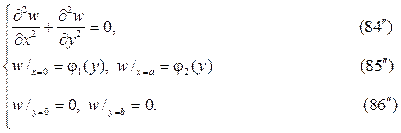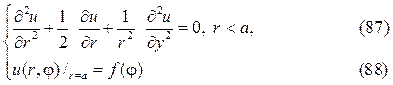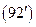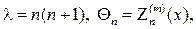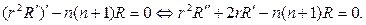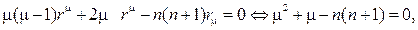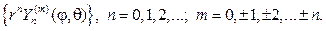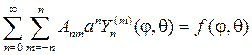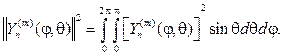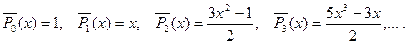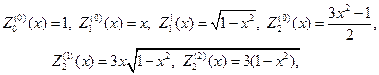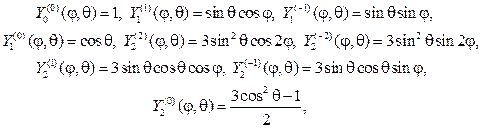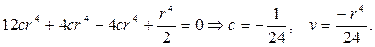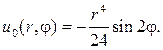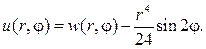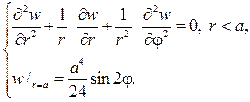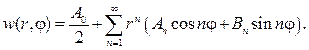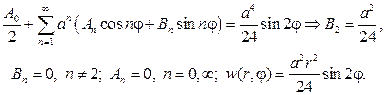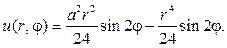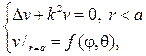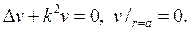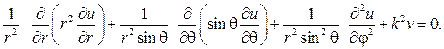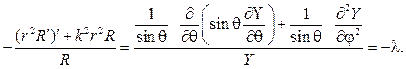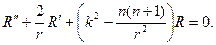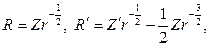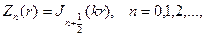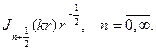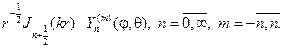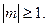Уравнение лапласа в прямоугольнике с граничными условиями

Уравнение лапласа в прямоугольнике с граничными условиями

Настоящая книга является естественным дополнением пособия А. Г. Свешникова, А. Н. Боголюбова, В. В. Кравцова «Лекции по математической физике». Её основная цель — помочь студентам приобрести необходимые практические навыки исследования математических моделей физических явлений, являющихся краевыми или начально-краевыми задачами для линейных дифференциальных уравнений в частных производных второго порядка. С этой целью каждая глава пособия построена следующим образом. В начале каждого параграфа главы приводятся необходимые минимальные сведения теоретического характера, используемые для решения данного типа задач. Затем эти методы демонстрируются в работе, для чего даются примеры решения конкретных задач. В конце главы приводятся задачи с ответами для самостоятельного решения.

Содержание пособия полностью соответствует курсу «Методы математической физики», читаемому на физическом факультете МГУ. Пособие написано на основе более чем двадцатилетнего опыта преподавания на физическом факультете Московского университета. Оно рассчитано в первую очередь на студентов физических специальностей университетов, но будет полезно и студентам инженерных специальностей и лицам, занимающимся математической физикой и прикладной математикой.

Авторы выражают свою глубокую благодарность заведующему кафедрой Московского государственного института электронной профессору А. С. Поспелову, профессорам А. В. Ефимову, А. С. Ильинскому и С. Я. Секерж-Зеньковичу, взявшим на себя труд ознакомиться с рукописью и сделавшим ряд ценных замечаний.

МЕТОД РАЗДЕЛЕНИЯ ДЛЯ УРАВНЕНИЙ

ЭЛЛИПТИЧЕСКОГО ТИПА

Краевые задачи для уравнения Лапласа в прямоугольнике (полупо- лосе), решаются методом разделения переменных в декартовых коорди- натах, в круговой областях (круг, сектор, кольцо) методом разделения пе- ременных в полярных координатах. При решении краевых задач для ци-линдрических и сферических областей используются соответственно ци- линдрические и сферические координаты бесселевы функции, полиномы и присоединённые функции Лежандра, а также шаровые функции. Возни- кающие здесь задачи Штурма Лиувилля своеобразны, их граничные ус- ловия определяются спецификой областей:

следует искать в виде суммы u(x,y)=v(x,y)+w(x,y),где v(x,y) и w(x,y) гар- монические функции в том же самом треугольнике, точнее они суть ре-шения краевых задач

Штрихованные краевые задачи решаются методом разделения пере- менных в терминах тригонометрических и гиперболических функций.

Рассмотрим задачу Дирихле для круга

где f(j)кусочно-непрерывная функция.

Следуя схеме метода Фурье полагаем

подставляем в (87) и разделяем переменные. В результате получим ра -венство

(90)

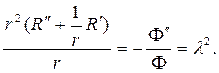
Угловая функция F(j) обязана быть периодической с периодом 2p. Присоединяя условие периодичности к дифференциальному уравнению для F(j), найдем задачу Штурма Лиувилля

откуда следует, что

(91)

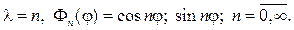
Возвращаясь к (80), решаем уравнение для радианальной функции. При

r 2 R² + rR¢ n 2 R = 0,

решение следует искать в виде степенной функции R=r m . Для определе- ния m получим соотношение

m(m 1)r m +m r m n 2 r m =0Û m 2 n 2 =0,

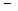
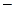
Если же n=0, то уравнение, как нетрудно проверить, rR² + R¢ =0имеет своими решениями функции

R₀(r) = 1; lnr.

С учетом (89) мы должны составить произведения угловых и радиаль- ных функций и получить набор функций, гармонических в круге

Если предположить, что ряд

(93)

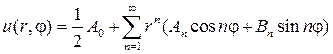
можно дифференцировать почленно дважды по r и j , то его сумма также будет гармонической функцией, т. е. будет решением уравнения (87). Подставляя (93) в (88), найдем

(94)

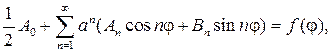
откуда с учетом формул коэффициентов Фурье следует

(95)

(96) Итог состоит в том, что решение задачи (87 88) дается рядом (93), коэффициенты которого определены равенствами (95-96).

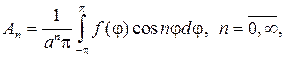
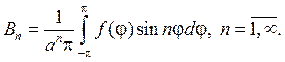
Замечание 1. Мы можем говорить, очевидно, что ряд (93) дает общий вид гармонической функции для круга r — n и lnr, поскольку они разрывны в

центре круга r=0.

Напротив, если рассматривать область r>a, то нельзя привлекать r — n и lnr, и общий вид гармонической функции для внешности круга будет да- ваться рядом

(97)

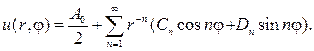
В случае кругового кольца a 2 q= 1-x 2 , найдем

(104¢)

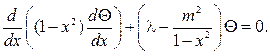
Соответственно и граничные условия (105) перейдут после замены в неравенства

(105′)

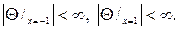
Задача (104¢) (105¢) есть известная задача для присоединенных функций Лежандра, ее решение (см., например, [3], стр. 115)

и возвращаясь к переменной q, найдем собственные значения и собствен- ные функции задачи (104), (105):

(106)

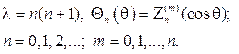
Составив произведения функций (106) на найденные выше функции F_m(j), получим множество решений уравнения (102)

(107)

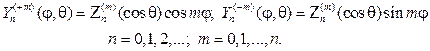
Эти решения принято называть сферическими функциями, их основ-ное свойство в приводимой ниже теореме.

Теорема 1. Сферические функции взаимно ортогональны на единич- ной сфере, т.е. при m₁¹m₂ или n₁¹n₂

(108)

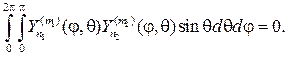
Теперь возвращаясь к равенству (101), возьмем уравнение для ради- альной функции

Оно имеет решение в виде степенной функции R=r m . Действительно, после подстановки

откуда находим значения m=n; (n+1) и соответственно решения

(109)

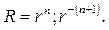
Умножая первые из функций (109) на сферические функции (107), получаем множество частных решений уравнения Лапласа в шаре:

Согласно схеме метода Фурье. составляем ряд с произвольными коэффи- циентами

(110)

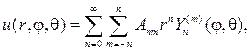
который будет гармонической функцией в шаре, если только его можно дифференцировать почленно.

Для нахождения коэффициентов А_nm подставим (110) в (100), тогда

и с учетом (108) найдем

(111)

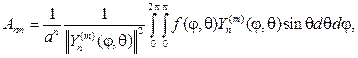
Последний интеграл вычисляется и при m=0 :

(112)

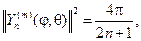
если же |m| ³ 1, то имеем

(113)

Завершая рассмотрение задачи (99),(100), скажем, что мы нашли ее решение в виде ряда (110), коэффициенты которого определяются в согласии с (111),(113).

Замечание 3. Напомним, что нормированные полиномы Лежандра вы- числяяются по формулам

(114)

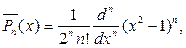
В свою очередь присоединенные функции Лежандра выражаются че- рез производные от полиномов Лежандра, т. е.

(115)

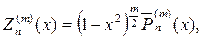
в частности будем иметь

(116)

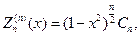
где С_n определенная константа.

С учетом (107), (115) и (116) выпишем несколько сферических функций:

(117)

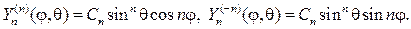
Замечание 4. При решении краевых задач для внешности шара вместо соотношения (110) нужно использовать ряд

(118)

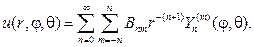
Общий вид гармонической функции в шаровом слое a 4 , и получим

Таким образом, частным решением будет функция

Вводим новую неизвестную функцию w(r,j) , полагая

Тогда относительно w(r,j) нужно решать задачу Дирихле для урав- нения Лапласа

Согласно (93), решение этой задачи дается формулой

Подставляя ее в граничное условие, получим

Ответом в задаче будет функция

254. Найдите решение первой краевой задачи для уравнения Гельмгольца

предполагая, что k не является собственным значением задачи

Р е ш е н и е. Запишем уравнение в сферических координатах

Беря u(r,j,q,)=R(r)Y(j,q), после разделения переменных придем к дифференциальным уравнениям:

Функция 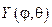будет решением уравнения (72), которое нужно решать при условии ограниченности и 2p-периодичности по j. В результате при- дем к сферическим функциям при l=n(n+1):

Относительно радиальной функции R(r) нужно решать дифференци- альное уравнение

Выполняя в этом уравнении замену

придем к соотношению относительно новой функции Z(r):

Последнее уравнение в качестве ограниченных в окрестности нуля

r=0 решений имеет бесселевы функции

соответственно будем иметь набор радиальных функций

Умножая их на сферические функции, получим набор решений урав- нения Гельмгольца:

Составляем ряд с числовыми коэффициентами

(119)

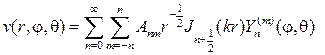
и определяем коэффициенты так, чтобы выполнялась граничное условие при r=a

где d = 4 при m = 0 и d =2 при

При найденных коэффициентах A_nm ряд (119) будет решением рассматриваемой краевой задачи для уравнения Гельмгольца.

255. Найдите такую гармоническую u(r,j,q) функцию внутри шарового слоя 1

Методика изложения темы «Решение краевых задач для уравнения Лапласа в прямоугольнике методом Фурье» Текст научной статьи по специальности « Математика»

Аннотация научной статьи по математике, автор научной работы — Попова Елена Михайловна, Чигирёва Ольга Юрьевна

В статье приводится методика изложения темы «Решение краевых задач для уравнения Лапласа в прямоугольнике методом Фурье» в курсе уравнений математической физики в МГТУ им. Н. Э. Баумана. Данный математический аппарат широко используется в физике, математической физике, электродинамике, квантовой механике, акустике, волновой оптике, теории колебаний, теории сигналов и цепей. Цель работы – помочь студентам приобрести навыки применения методов математической физики к решению различных физических задач. Одним из основных методов решения задач математической физики является метод Фурье (разделения переменных). Задача Штурма – Лиувилля – важный этап этого метода. Для того чтобы структурировать основные типы задач Штурма – Лиувилля, в статье приведена таблица, в которой максимально лаконично представлен материал. В работе также кратко приведены основные теоретические сведения и в качестве примера решена краевая задача для уравнения Лапласа в прямоугольнике. Статья будет полезна студентам приборостроительных специальностей, а также преподавателям соответствующих курсов.

Похожие темы научных работ по математике , автор научной работы — Попова Елена Михайловна, Чигирёва Ольга Юрьевна

Текст научной работы на тему «Методика изложения темы «Решение краевых задач для уравнения Лапласа в прямоугольнике методом Фурье»»

научно-методический электронный журнал

Попова Е. М., Чигирёва О. Ю. Методика изложения темы «Решение краевых задач для уравнения Лапласа в прямоугольнике методом Фурье» // Научно-методический электронный журнал «Концепт». — 2018. — № У9. — 0,4 п. л. -иН1: http://e-koncept.ru/2018/186085.htm.

ART 186085 УДК 378.147

Попова Елена Михайловна,

кандидат физико-математических наук, доцент ФГБОУ ВО «Московский государственный технический университет им. Н. Э. Баумана», г. Москва elmipo@yandex.ru

Чигирёва Ольга Юрьевна,

кандидат физико-математических наук, доцент ФГБОУ ВО «Московский государственный технический университет им. Н. Э. Баумана», г. Москва m kfn 12@yandex. ru

Методика изложения темы «Решение краевых задач для уравнения Лапласа

в прямоугольнике методом Фурье»

Аннотация. В статье приводится методика изложения темы «Решение краевых задач для уравнения Лапласа в прямоугольнике методом Фурье» в курсе уравнений математической физики в МГТУ им. Н. Э. Баумана. Данный математический аппарат широко используется в физике, математической физике, электродинамике, квантовой механике, акустике, волновой оптике, теории колебаний, теории сигналов и цепей. Цель работы -помочь студентам приобрести навыки применения методов математической физики к решению различных физических задач. Одним из основных методов решения задач математической физики является метод Фурье (разделения переменных). Задача Штурма -Лиувилля — важный этап этого метода. Для того чтобы структурировать основные типы задач Штурма — Лиувилля, в статье приведена таблица, в которой максимально лаконично представлен материал. В работе также кратко приведены основные теоретические сведения и в качестве примера решена краевая задача для уравнения Лапласа в прямоугольнике. Статья будет полезна студентам приборостроительных специальностей, а также преподавателям соответствующих курсов.

Ключевые слова: метод Фурье разделения переменных, задача Штурма — Ли-увилля, уравнение Лапласа.

Раздел: (01) отдельные вопросы сферы образования.

При подготовке студентов приборостроительных специальностей важную роль играет изучение аналитических методов решения задач математической физики [1]. Одним из таких методов является метод Фурье разделения переменных 4, согласно которому решение ищется в виде разложения в ряд Фурье по системе собственных функций задачи Штурма — Лиувилля.

Для успешного освоения студентами данной темы в работе приводятся необходимые теоретические сведения из функционального анализа [5]. Особое внимание уделено рассмотрению задачи Штурма — Лиувилля. Изложенный материал включает постановку задачи, свойства собственных значений и собственных функций [6]. Приведена таблица, в которую сведены наиболее часто встречающиеся типы задач Штурма — Лиувилля для отрезка [7]. Работа содержит краткие теоретические сведения, связанные с постановкой краевых задач для уравнения Лапласа; доказательства сформулированных теорем можно найти в [8, 9]. Показан пример решения краевой задачи для уравнения Лапласа в прямоугольной области.

Структурированный подход к изложению материала, сочетающий основные теоретические сведения и подробно разобранный пример решения краевой задачи, позволяет студентам не только овладеть математическим аппаратом, но и научиться применять его при решении прикладных задач.

1бб1\1 2эо4-12ох Попова Е. М., Чигирёва О. Ю. Методика изложения темы «Решение краевых задач для уравнения Лапласа в прямоугольнике методом Фурье» // Научно-методический электронный журнал «Концепт». — 2018. — № У9. — 0,4 п. л. -иН1: http://e-koncept.ru/2018/186085.htm.

научно-методический электронный журнал

Для описания стационарных процессов в физике обычно используют уравнения эллиптического типа. Наиболее распространенным уравнением этого типа является уравнение Лапласа

где A — дифференциальный оператор 2-го порядка, называемый оператором Лапласа.

К уравнению Лапласа приводят задачи о стационарном тепловом состоянии однородного тела, равновесном распределении электрических зарядов на поверхности проводника, об установившемся движении несжимаемой жидкости и многие другие.

При решении краевых задач для уравнения Лапласа используют различные аналитические методы: метод Фурье разделения переменных, метод функции Грина и метод интегральных преобразований. В данной работе рассматривается метод Фурье разделения переменных.

Гильбертово пространство l2 ([ a, b]; р)

Линейное пространство, в котором задана норма, называют нормированным пространством.

Нормированное пространство называют полным или банаховым пространством, если в нем любая фундаментальная последовательность сходится.

Гильбертовым пространством называют бесконечномерное банахово пространство, норма в котором индуцирована скалярным произведением

Примером гильбертова пространства является пространство функций, суммируемых с квадратом на отрезке [a,b] с весом р(x) > 0:

jр(x)/2 (x)dx 0, q(x) e С [a, b], q(x) > 0.

Этот оператор называют оператором Штурма — Лиувилля. К области определения D (L) оператора L отнесем множество функций f е С2 (a, b)п С1 [a, b], удовлетворяющих условию L [f ]e L2 [a, b] и однородным граничным условиям

-af ‘(a) + Pf (a) = 0 , af ‘(b) + PJ (b) = 0, где a, P = const > 0, причем a + P > 0, i = 1,2.

Свойства оператора L:

1) (L [f], g) = (f, L [g]), f, g e D (L );

2) (L [f], f )> 0, f e D(L) .

Задача Штурма — Лиувилля

Рассмотрим следующую краевую задачу с однородными граничными условиями на отрезке [a, b]:

L [X(x)] = 1р(x)X(x), a 0; a, P = const > 0, причем a+P> 0, i = 1,2.

Задачу (1), (2) называют задачей Штурма — Лиувилля. Она состоит в нахождении значений 1, при которых уравнение (1) имеет ненулевые решения X (x) из области определения оператора L . Такие значения 1 называют собственными значениями оператора L , а соответствующие им нетривиальные решения X (x) — собственными функциями оператора L.

Свойства собственных значений и собственных функций задачи Штурма — Лиувилля

1. Множество собственных значений <1„>«=1 счетно. При этом каждому собственному значению 1п соответствует с точностью до числового множителя только одна собственная функция Xn (x).

2. Все собственные значения неотрицательны: 1п> 0, n е N и <0>. Значение 1 = 0 может быть собственным значением оператора L только при q(x) = 0 и P = P = 0.

3. Собственные функции Xn (x) и Xm (x), отвечающие различным собственным значениям 1п и 1т, ортогональны на отрезке [a,b] с весом р(x), т. е.

issN 2304-i20x Попова Е. М., Чигирёва О. Ю. Методика изложения темы «Решение краевых задач для уравнения Лапласа в прямоугольнике методом Фурье» // Научно-методический электронный журнал «Концепт». — 2018. — № V9. — 0,4 п. л. -URL: http://e-koncept.ru/2018/186085.htm.

научно-методический электронный журнал

Задача 3: ax = Д = 0 Т 2n — 1)J2 Я = ( n ) , n е N; V 21 J

научно-методический электронный журнал

Попова Е. М., Чигирёва О. Ю. Методика изложения темы «Решение краевых задач для уравнения Лапласа в прямоугольнике методом Фурье» // Научно-методический электронный журнал «Концепт». — 2018. — № V9. — 0,4 п. л. -URL: http://e-koncept.ru/2018/186085.htm.

Задача Штурма — Лиувилля

Собственные значения и собственные функции задачи Штурма — Лиувилля

где / (Р), g (Р), И (Р) и у(Р)> 0 (у(Р)^ 0) — функции, заданные на границе Е области О; Я — внешняя нормаль к границе Е.

Если область, в которой поставлена краевая задача, ограничена, то такая задача называется внутренней.

Далее сформулируем основные свойства 1-й и 2-й внутренних краевых задач на плоскости.

1. Решение внутренней задачи Дирихле на плоскости единственно.

2. Внутренняя задача Дирихле на плоскости разрешима при любой непрерывной функции / (Р).

3. Решение внутренней задачи Неймана на плоскости определяется с точностью до произвольной аддитивной постоянной.

4. Внутренняя задача Неймана на плоскости разрешима при любой непрерывной функции g (Р), удовлетворяющей условию

$Я(Р) Не можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

где /1 (х) = 4и0 — 1 — I, /2 (х) = и би

issn 2304-120X Попова Е. М., Чигирёва О. Ю. Методика изложения темы «Решение краевых задач для уравнения Лапласа в прямоугольнике методом Фурье» // Научно-методический электронный журнал «Концепт». — 2018. — № V9. — 0,4 п. л. -URL: http://e-koncept.ru/2018/186085.htm.

научно-методический электронный журнал

Решение. Согласно методу Фурье, решение u (x, y) краевой задачи (3)-(5) будем искать в следующей форме:

u (x, y ) = X (x) Y (y 0. (6)

Запишем дифференциальный оператор A, стоящий в левой части уравнения

(3), в виде A = ——L , где L =—. Далее подставим предполагаемую форму реше-

ния (6) в уравнение (3):

X ( x ) Y'( y )-Y ( y ) L [ X (x )] = 0. После разделения переменных получим соотношение: L [ X (x)] Y •( y) X (x) = Y (y)» •

В результате уравнение (3) в частных производных «распадается» на два дифференциальных уравнения:

L [ X (x)] = 1X (x), 0 Не можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

5. Kolmogorov, A. N. & Fomin, S. V. (1972). Jelementy teorii funkcij i funkcional’nogo analiza, Nauka, Moscow (in Russian).

6. Vladimirov, V. S. (1988). Op. cit.

научно-методический электронный журнал

Попова Е. М., Чигирёва О. Ю. Методика изложения темы «Решение краевых задач для уравнения Лапласа в прямоугольнике методом Фурье» // Научно-методический электронный журнал «Концепт». — 2018. — № V9. — 0,4 п. л. -URL: http://e-koncept.ru/2018/186085.htm.

7. Feoktistov, V. V. & Chigirjova, O. Ju. (2015). Uravnenija matematicheskoj fiziki i special’nye funkcii: metod. ukazanija k vypolneniju domashnego zadanija, Izd-vo MGTU im. N. Je. Baumana, Moscow (in Russian).

8. Vladimirov, V. S. (1988). Op. cit.

9. Sveshnikov, A. G., Bogoljubov, A. N. & Kravcov, V. V. (2004). Op. cit.

Рекомендовано к публикации:

Горевым П. М., кандидатом педагогических наук, главным редактором журнала «Концепт»

Поступила в редакцию Received 14.06.18 Получена положительная рецензия Received a positive review 10.07.18

Принята к публикации Accepted for publication 10.07.18 Опубликована Published 30.09.18

Creative Commons Attribution 4.0 International (CC BY 4.0) © Концепт, научно-методический электронный журнал, 2018 © Попова Е. М., Чигирёва О. Ю., 2018