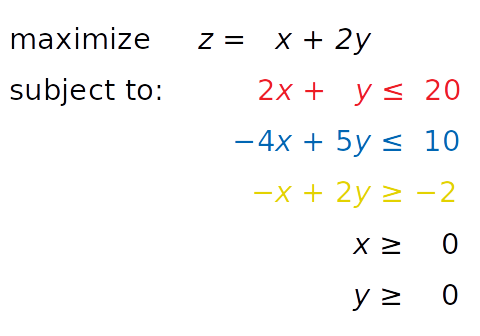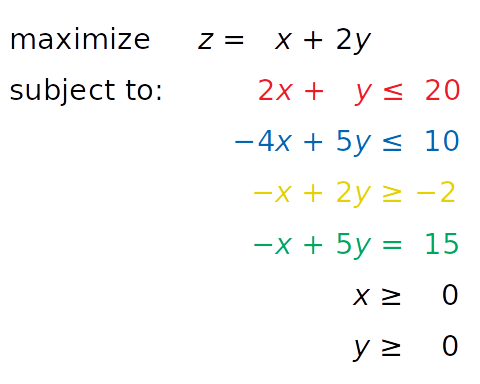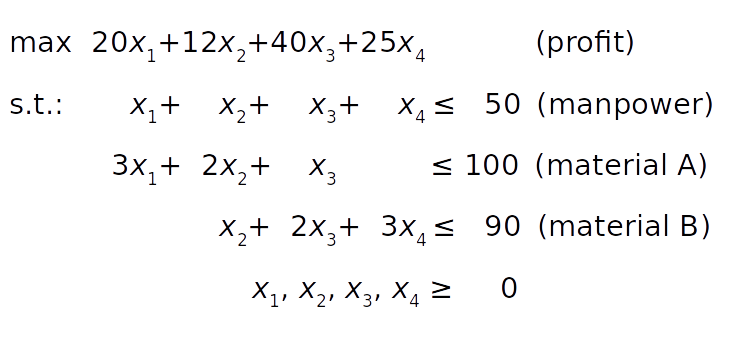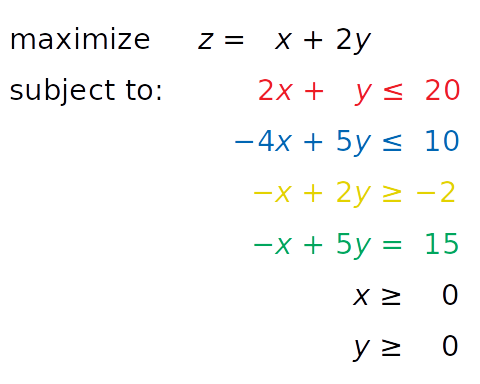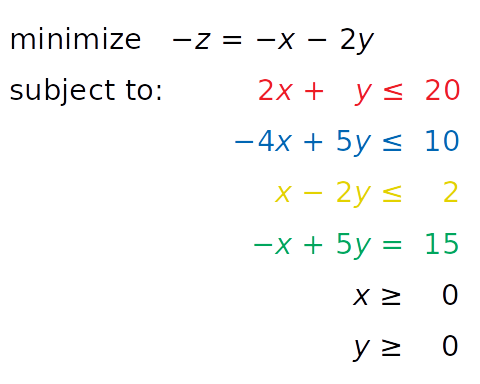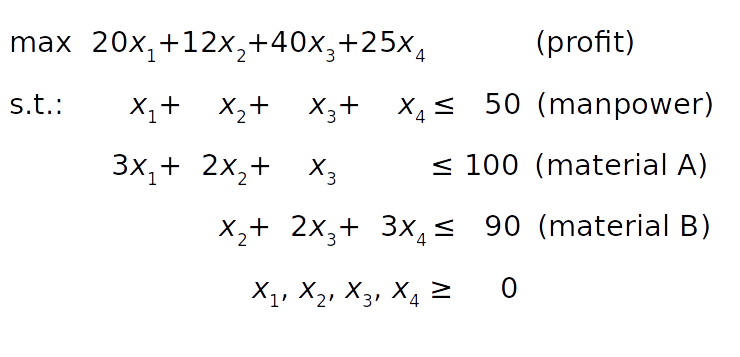Уравнение линейное программирование если нет решения

Решение задач линейного программирования

Решение происходит в три этапа:

1. Переход к КЗЛП. Любая ЗЛП вида ax ≤ b , ax ≥ b , ax = b ( F(X) → extr ) сводится к виду ax = b , F(X) → max ;
2. Переход к СЗЛП. КЗЛП вида ax = b сводится к виду ax ≤ b , F(X) → max ;
3. Решение симплексным методом;

• Шаг №1
• Шаг №2
• Видеоинструкция
• Оформление Word

Переход от задачи минимизации целевой функции к задаче максимизации

Задача минимизации целевой функции F(X) легко может быть сведена к задаче максимизации функции F*(X) при тех же ограничениях путем введения функции: F*(X) = -F(X) . Обе задачи имеют одно и то же решение X*, и при этом min(F(X)) = -max(F*(X)) .
Проиллюстрируем этот факт графически:

F(x) → min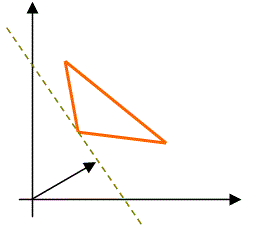

F(x) → max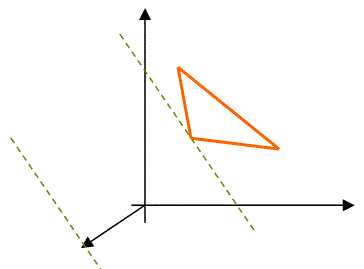

Для оптимизации функции цели используем следующие понятия и методы.
Опорный план – план с определёнными через свободные базисными переменными.
Базисный план – опорный план с нулевыми базисными переменными.
Оптимальный план – базисный план, удовлетворяющий оптимальной функции цели (ФЦ).

Ведущий (разрешающий) элемент – коэффициент свободной неизвестной, которая становится базисной, а сам коэффициент преобразуется в единицу.
Направляющая строка – строка ведущего элемента, в которой расположена с единичным коэффициентом базисная неизвестная, исключаемая при преобразовании (строка с минимальным предельным коэффициентом, см. далее).
Направляющий столбец – столбец ведущего элемента, свободная неизвестная которого переводится в базисную (столбец с максимальной выгодой, см. далее).

Переменные x₁, …, x_m, входящие с единичными коэффициентами только в одно уравнение системы, с нулевыми – в остальные, называются базисными или зависимыми. В канонической системе каждому уравнению соответствует ровно одна базисная переменная. Переход осуществляется с помощью метода Гаусса–Жордана. Основная идея этого метода состоит в сведении системы m уравнений с n неизвестными к каноническому виду при помощи элементарных операций над строками.
Остальные n-m переменных (x_m+1,…, x_n) называются небазисными или независимыми переменными.

Базисное решение называется допустимым базисным решением, если значения входящих в него базисных переменных x_j≥0, что эквивалентно условию неотрицательности b_j≥0.
Допустимое базисное решение является угловой точкой допустимого множества S задачи линейного программирования и называется иногда опорным планом.
Если среди неотрицательных чисел b_j есть равные нулю, то допустимое базисное решение называется вырожденным (вырожденной угловой точкой) и соответствующая задача линейного программирования называется вырожденной.

Симплексный метод решения задач линейного программирования

Симплексный метод решения задач линейного программирования

Введение

Задача линейного программирования (ЗЛП) состоит в определении значений упорядоченной совокупности переменных x_j, j = 1(1)n при которых линейная целевая функция достигает экстремального значения и при этом выполняются (удовлетворяются) все ограничения (они также линейные) в форме равенств или неравенств. Требуется найти план Х = , который обеспечивает получение целевой функцией с экстремальным значением. Идеи моделей линейного планирования (программирования) впервые были высказаны и опубликованы советским математиком Л. В. Канторовичем в 1939 году в работе «математические методы организации и планирования производства». В 1975 году Л. В. Канторович и Т. Купманс получили Нобелевскую премию по экономическим наукам с формулировкой «за их вклад в теорию оптимального распределения ресурсов». В 1947 г. очень близкие идеи высказаны американским математиком Дж. Данцигом. А еще позднее стали массово появляться работы, посвященные проблемам выбора оптимальных решений в силу их исключительной важности. Признание приоритета за Л. В. Канторовичем не оспаривалось практически никогда, а после присуждения Нобелевской премии тем более.

Общая постановка задачи

Задача линейного программирования (ЗЛП) состоит в определении значений упорядоченной совокупности переменных x_j, j = 1(1)n при которых линейная целевая функция достигает экстремального значения и при этом выполняются (удовлетворяются) все ограничения в форме равенств или неравенств. Требуется найти план Х = , который обеспечивает получение целевой функцией экстремального значения

а) Если система ограничений ЗЛП обладает хотя бы одним решением, она называется совместной в противном случае несовместной; б) Допустимое множество решений ЗЛП не пусто, если система ограничений совместна; в) Множество допустимых решений ЗЛП (если оно не пусто) в общем случае является многогранным множеством. Линейная функция Q(X ) называется функцией цели, целевой функцией (ЦФ), множество планов <X > удовлетворяющих системе ограничений (2) – (5), ­­- множеством допустимых решений (альтернатив) и обозначается символом R, X є Ω Допустимый план X є Ω, доставляющий целевой функции (1) экстремальное значение, называется оптимальным. Задача в форме (1) – (5) представляет общую задачу линейного программирования.

Cтандартная форма задачи

Если все ограничения задачи заданы в виде строгих равенств и на переменные величины наложено условие неотрицатаельности x_j ≥0, j = 1(1)n, то такую формулировку называют стандартной:

Экстремумы функций в общем случае связаны простыми соотношениями

Переход от общей задачи к стандартной

Для удобства применения методов решения выполняют преобразование исходной общей задачи. Ограничения неравенства преобразуют в равенства. Вводятся дополнительные переменные по числу неравенств, т. е. формулируют расширенную задачу x_n+1 ≥0, x_n+2 ≥0, . , x_n+k ≥0. Неравенства a_i1x₁+a_i2x₂+. +a_inx_n ≥b_i введением переменной x_n+1≥0 преобразуются в равенства a_i1x₁+a_i2x₂+. +a_inx_n + a_i(n+1)x_n+1=b_i. В ЦФ вновь введённые переменные имеют коэффициенты равные нулю c_n+1=c_n+2=. =c_n+k =0.

а) Если в исходной общей задаче на некоторые переменные x_j , j = 1(1)n, не наложено условие их неотрицательности, то каждую такую переменную представляют в виде разности положительных новых переменных x’_j — x»_j , где x’_j≥0 и x»_j≥0 , j>r . Способ устранения отрицательных переменных прост, но при этом размерность (число неотрицательных переменных) задачи возрастает. б) Имеется другой более сложный путь. Каждую x_j ≯ 0 выражают явно через другие, для которых условие x_j ≥0 выполняется. Затем найденные выражения подставляют в ограничения, чтобы исключить их из рассмотрения. При этом размерность задачи даже уменьшается.

Каноническая форма задачи

Удобство этой формы ЗЛП состоит в том, что она позволяет предельно просто получить первое допустимое решение. Для этой формы должны быть выполнены условия:

правые части в ограничениях – неотрицательны b_i ≥ 0, i = 1(1)m;

каждое уравнение содержит переменную x_j ≥0 с коэффициентом при ней равным “1” в этом уравнении и с коэффициентом “0” во всех других уравнениях; эти переменные называют дополнительными или искусственными;

в ЦФ эти переменные входят с коэффициентом “0”;

определение опорного плана (начальной вершины) выполняют методом искусственного базиса, что ещё до решения задачи позволяет выяснить факт существования решения.

Если исходная задача имеет хотя бы один план, то расширенная задача (после введения искусственных переменных в систему ограничений) также содержит этот план в качестве своего допустимого решения

Переменные x₁, x₂, . x_m называют базисными – остальные свободными (внебазисными). Вершина допустимой области решений записывается в виде точки , так как векторы условий для x₁, x₂, . x_m являются линейно независимыми (образуют подматрицу, где единицы помещаются только на главной диагонали).

Геометрическая интерпретация ЗЛП

Будем рассматривать пример ЗЛП в производстве двух видов продукции на предприятии, использующем при этом четыре виды сырья (см. ранее эту задачу). Этот пример удобен для геометрической интерпретации тем, что пространство решений является двумерным (т. е. плоскость) и все элементы ЗЛП допускают наглядное представление (изображение) в трёхмерном пространстве. Начнём с рассмотрения системы неравенств (ограничений ЗЛП). Заметим, что каждое i-е неравенство в ограничениях ЗЛП определяет полуплоскость в системе координат х₁Ох₂ с граничной прямой a_i1x₁ + a_i2x₂ = b_i , i = 1(1)m.

Рисунок 1 — Примеры областей, рписывающих ограничения, задачи линейного программирования

Выпишем их и присвоим им имена

Область, формируемая полуплоскостями, может быть получена в виде замкнутого или разомкнутого (неограниченного) многогранника. Путём непосредственного построения границ (прямых) и выявления области пересечения полупространств выясним, является ли многогранное множество ограниченным и не пусто ли оно (рис.). Имеем на плоскости х₁ О х₂ многоугольник А Ո В Ո C Ո D Ո E Ո F . Он является выпуклым (всегда ли?), его граница образована отрезками прямых.

Целевая функция. Что можно сказать о линейной форме (ЦФ)? Это функция двух переменных x₁ и x2, её образ в трёхмерном пространстве – плоскость, проходящая через начало координат. Найдём частные производные ЦФ по х_j

Так как частная производная по переменной х_j представляет наибольшую скорость изменения функции Q в направлении этой оси, то вектор C = — это вектор наибольшего изменения ЦФ, вектор градиентного направления. Если значения Q зафиксировать Q =Q₁ = const , то уравнение ЦФ превращается в уравнение прямой c₁x₁ + c₂x₂= Q₁= const плоскости х₁О х₂

В трёхмерном пространстве это плоскость параллельная х₁О х₂ на высоте Q₁, в каждой точке которой значение ЦФ постоянно и равно Q₁. . На плоскости Q этой прямой соответствует линия параллельная плоскости х₁О х₂, которую называют линией уровня (плотницкий уровень) функции c₁x₁ + c₂x₂ . Изменяя Q, получим семейство линий уровня параллельных друг другу. Требованию задачи – поиску экстремума Q соответствует смещение точки по поверхности функции Q в направлении вектора C = от начала координат.

Ограничения ЗЛП не позволяют аргументам ЦФ Q(x1, x2) выходить за пределы многоугольной допустимой области. Другими словами, надо найти точку на плоскости Q наиболее удалённую от плоскости х₁О х₂ и проекция которой на х₁О х₂ лежит в области допустимых решений. Координаты x*₁, x*₂ найденной точки и определяют оптимальный план ЗЛП. Покажем, что семейство линий уровня (изолиний) перпендикулярно C , т. е. перпендикулярно прямой х₂ =с₂х₁/c₁. Из векторного анализа известно, что все линии уровня ЦФ Q перпендикулярны вектору градиенту ЦФ, вычисленному в некоторой точке

Таким образом, перемещаясь вдоль вектора C или по прямой х₂ =с₂х₁/c₁, легко построить линию уровня (она перпендикулярна х₂ = с₂х₁/c₁ ) и вычислить значение ЦФ Q для этой линии. Экстремум Q, очевидно, будет достигаться в положении касания линией уровня (её проекцией) границы множества допустимых решений. Такое касание может быть трёх типов: в вершине, по ребру, по грани многогранника. Этим типам касания соответствуют: единственное решение в вершине и бесконечное множество решений в других случаях. Область допустимых решений. Рассмотрим случаи ограниченной и неограниченной области допустимых решений. В последнем случае поиск экстремума Q может приводить к отсутствию решения, так как extr Q → ±∞ или существует опорная прямая линия, касающаяся неограниченного многогранника, и тогда решение существует.

Пример. Описание области допустимых решений.

Рисунок В — Область допустимых решений ЗЛП

Мы можем записать уравнение границы области D заданной неравенствами:

Основные понятия и теоремы линейной алгебры Важным понятием линейной алгебры является понятие линейного векторного пространства. Определение 2.1. Упорядоченная совокупность n действительных чисел называется n-мерным вектором. Определение 2.2. Совокупность всевозможных n-мерных векторов после введения в нее операций сложения и умножения на действительное число называется n-мерным линейным векторным пространством. Частными случаями линейных пространств являются прямая, плоскость, трехмерное пространство. Определение 2.3. Система векторов X₁, X₂, . X_n называется линейно зависимой, если существуют такие числа λ₁, λ₂, …, λ_n, не равные нулю одновременно, при которых имеет место равенство: λ₁X₁+ λ₂X₂ …+ λ_n X_n=0 , где все λ_i ≥0 и λ₁+ λ₂+ …+ λ_n =1. Если же это равенство возможно лишь в случае, когда все λ_i = 0 (i = 1(1)n) , то система векторов называется линейно независимой. Определение 2.4. Базисом n-мерного векторного пространства называется любая совокупность n линейно независимых векторов этого пространства. В двумерном пространстве за базис могут быть взяты любые два неколлинеарных вектора, в частности, е₁ = (1,0), е₂ = (0, 1). В трехмерном пространстве – любые три некомпланарных вектора, например, е₁ = (1,0,0), е₂ = (0,1,0), е₃ = (0,0,1).

Выпуклой линейной комбинацией точек X₁, X₂, . X_n называется линейная комбинация вида: X= λ₁X₁+ λ₂X₂ …+ λ_n X_n где все λ_i ≥0 и λ₁+ λ₂+ …+ λ_n =1. В частности, когда имеются две точки X₁ и X₂, то их выпуклая комбинация λX₁+(1- λ)X₂, λ ∈[0,1] представляет собой точку на отрезке, соединяющем эти точки.

Теорема 1. Любой вектор n-мерного векторного пространства можно представить, как линейную комбинацию векторов базиса, притом единственным образом. Определение 2.5. Максимальное число линейно независимых векторов линейного пространства называется размерностью линейного пространства. Линейное пространство обычно обозначают, R_n где n – его размерность. Выпуклой оболочкой точек называется множество всевозможных выпуклых комбинаций этих точек. Множество называется выпуклым, если вместе с двумя любыми его точками оно содержит и их произвольную выпуклую линейную комбинацию. С геометрической точки зрения это означает, что выпуклое множество содержит вместе с любыми двумя своими точками и соединяющий их отрезок. Выпуклое множество совпадает со своей выпуклой оболочкой. Примерами выпуклых множеств являются прямолинейный отрезок, квадрат, круг, прямая, полуплоскость, куб, шар, полупространство и другие. Угловыми точками выпуклого множества называются точки, не являющиеся выпуклой линейной комбинацией двух произвольных точек множества. Например, угловыми точками треугольника являются его вершины, угловыми точками круга – точки окружности. Таким образом, выпуклое множество может иметь конечное или бесконечное число угловых точек, но может не иметь их совсем. Например, прямая, плоскость, полуплоскость, пространство, полупространство угловых точек не имеют. Одним из основных понятий теории линейного программирования является понятие выпуклого многогранника в n-мерном пространстве, частными случаями которого являются при n = 1 отрезок на прямой, при n = 2 выпуклый многоугольник на плоскости. Выпуклым многоугольником называется выпуклое замкнутое ограниченное множество точек на плоскости, имеющее конечное число угловых точек, называемых вершинами. Прямолинейные отрезки, соединяющие две вершины и образующие границу, называются сторонами многоугольника.

Опорной прямой выпуклого многоугольника называется прямая, имеющая с многоугольником, расположенным по одну сторону от нее, хотя бы одну общую точку.

Выпуклым многогранником называется выпуклое замкнутое ограниченное множество точек пространства, имеющее конечное число угловых точек, называемых его вершинами. Многоугольники, ограничивающие многогранник, называются его гранями, а отрезки, по которым пересекаются грани, называются ребрами. Опорной плоскостью многогранника называется плоскость, имеющая с многогранником, расположенным по одну сторону от нее, хотя бы одну общую точку.

Теорема 2.2. Выпуклый n-мерный многогранник является выпуклой линейной комбинацией своих угловых точек.

Следствие 2.3. Из теоремы вытекает, что выпуклый многогранник порождается своими угловыми точками (вершинами): отрезок – двумя точками, треугольник – тремя точками, n – угольник на плоскости – n точками и т. д. В тоже время выпуклая многогранная область, содержащая бесконечно удаленную точку, являясь неограниченным множеством, не определяется однозначно своими угловыми точками: любую ее точку нельзя представить в виде выпуклой линейной комбинации угловых точек.

Элементы выпуклых множеств

Определение 1. Множеством называется совокупность элементов любой природы, для которых задано правило принадлежности к данному множеству.

Определение 2. е — о к р е с т н о с т ь ю точки х называется множество всех точек, расстояние которых до точки х меньше е.

Определение 3. Точка х₁ называется внутренней точкой множества M, если существует такая — окрестность данной точки, все точки которой принадлежат множеству M.

Определение 4. Точка х₂ называется в н е ш н е й т о ч к о й м н о ж е с т в а M, если существует такая — окрестность данной точки, все точки которой не принадлежат множеству М.

Определение 5. Точка х₃ называется г р а н и ч н о й т о ч к о й м н о ж е с т в а M, если в любой её — окрестности существуют точки как принадлежащие множеству M, так и не принадлежащие этому множеству.

Определение 6. Множество М называется з а м к н у т ы м, если оно содержит все свои граничные точки. х 2— незамкнутое множество, Пример. х 2 — замкнутое множество.

Определение 7. Множество М называется в ы п у к л ы м, если вместе с любыми двумя точками, принадлежащими данному множеству, оно содержит и отрезок их соединяющий. В общей форме ЗЛП каждый символ R1, R2, …, Rm означает один из знаков: = или ≠. В такой форме задачи линейного программирования часть переменных может быть подчинена условию неотрицательности (x_i ≥ 0), часть – условию неположительности (x_j ≤ 0), а какие-то переменные, возможно, могут принимать любые значения.

Общий алгоритм симплексного метода ЗЛП

Пусть система невырожденна и совместна, т.е. r_A = r_B = r = m

Все введённые переменные в новых обозначениях удобно свести в таблицу, которая называется симплексной.

Алгоритм решения

1) Формируем исходный план при свободных переменных; x_j =0, j = m+1(1)n, x_j = β_ф, ф = 1(1)m при β_ф > 0 план x o допустим Q(x) =x_o.

2) Проверяем этот план на оптимальность, используя значения γ_j коэффициентов ЦФ в последней строке таблицы. Могут быть два случая:

а) все γ_j ≤0, j = m+1(1)n , при этом увеличение никакой переменной (из свободных) не приведёт к уменьшению ЦФ Q, т. е. план x o улучшить нельзя, и он уже оптимален, таким образом, условием оптимальности плана является – отсутствие в таблице γ_j >0.

б) некоторые γ_j > 0. В этом случае увеличение значений соответствующих свободных переменных x_j (γ_j > 0) будет минимизировать Q, так как

Чтобы Q уменьшалось, такие переменные следует вводить (последовательно) в базис, но, чтобы размерность пространства не изменялась из базиса должны выводиться переменные в число свободных (по одной) формируем множество индексов Г = < j | γ_j >0>. Какая переменная должна первой вводиться в базис? Вообще последовательно перебирая (вершины симплекса) решение отыскивается при произвольном выборе, но для определённости выбираем новую базисную переменную с индексом v = argmax <x_j>, где j ∈ Г. Теперь определим переменную (базисную), которая будет выводиться из базиса.

В системе уравнений

Начинаем увеличивать х_v до тех пор, пока некоторый х_ф станет отрицательным. Первый же х_ф ≤ 0 будет выводиться из базиса. Определение. Столбец с индексом v и строка с индексом ф = i называются направляющими.

3) Проверка существования решения (ограниченность ЗЛП). В выражениях, связывающих х, ∝, β, х_ф = β_ф -∝_фvх_v, ф=1(1)m, могут быть все ∝_фv 0. Пусть ЦФ ограничена и некоторые ∝_фv > 0. Сформируем множество индексов S = < ф | ∝_фv >0>. Из базиса необходимо выводить переменную с индексом i, так как она первая обращается в нуль, i = argmin(β_ф/∝_фv), где ф∈S, таким образом, базисная переменная x_i выводится из базиса.

Определение. Коэффициент ∝_фv=∝_iv , стоящий на пересечении направляющих строки и столбца называется направляющим (разрешающим, генеральным) элементом таблицы.

4) Формируем новые множества:

Дальнейшие действия алгоритма:

преобразуем задачу, т.е. все базисные переменные и целевую функцию выражаем через свободные переменные;

заполняем новую симплексную таблицу;

делаем все свободные переменные х_j = 0 и находим опорный план;

Опорный план (вектор) такой Х’ = ; Q(Х’ ) ≤ Q₀ ;

если план не оптимален, то определяем направляющий столбец;

проверяем существует ли оптимальный план;

если оптимальный план существует, то находим направляющую строку и вновь изменяем базис и т. д.

Переход от одной таблицы к другой связан с трудоемкими расчетами (о чем надо еще написать) Вводимую в базис переменную х_ν (икс ню) выражаем через свободные переменные и выводимую х_i. Действуем так.

При ручном счете все эти действия проще выполнять с использованием вспомогательных таблиц по правилам специального алгоритма. Эти таблицы имеют прежнюю структуру, но клетки делятся на две полуклетки. В верхней полуклетке оставляем содержимое из прежней таблицы.

Рисунок С — Структурная схема алгоритма симплекс-метода

При решении задач линейного программирования вычисляются ранги у матрицы ограничений и расширенной матрицы ранги должны быть равны r=m.

Матрица и её ранг. Система mn чисел, расположенных в форме прямоугольной таблицы из m строк и n столбцов, называется матрицей.

Определение. Рангом матрицы [A] называется наибольший порядок, который могут иметь её миноры, не обращающиеся в нуль. Для определения ранга матрицы следует рассмотреть все её миноры порядка р (где р – меньшее из чисел m, n, если m ≠ n или р = m = n); если хотя бы один из них ≠ 0, то ранг [A] равен р; если же все они равны (= 0), то следует рассмотреть все миноры порядка р – 1 и т. д. Практически поступают наоборот: переходят от миноров меньшего порядка к минорам большего порядка, в соответствии со следующим правилом. Если найден минор k-го порядка D_k, отличный от нуля, то остается вычислить только те миноры (k + 1) -го порядка, которые представляют собой «окаймление» D_k, например,

Определение. Минором k-го порядка матрицы [A] (k ≤ m, k ≤ n) называется определитель D, составленный (с сохранением порядка) из k 2 элементов матрицы, лежащих на пересечении некоторых её k столбцов и k строк См. схему выше минор D из 3-х строк и 3-х столбцов. Обозначается матрица символами:

Матрица А и ее миноры с различным окаймлением

Приведем пример вычисления ранга матрицы.

С выполнением каждого шага связаны процедуры:

1. Получение опорного плана; 2. устанавливается, является ли данный опорный план оптимальным; 3. если нет, то существует ли оптимальный план вообще, или задача является неограниченной; 4. если оптимальный план существует, то, как перейти на следующем шаге, к новому опорному плану с меньшим значением ЦФ.

Алгоритм СМ применяется к ЗЛП после её приведения к канонической форме, т.е. отыскивается минимум целевой функции min Q(X) на множестве векторов Х .

Система ограничений совместна r_A = r_B и detA ≠ 0 невырожденная, т.е. ранг r =m матрицы A_{[m, n]} и расширенной матрицы системы равен m. Имеется множество решений. Для решения системы произвольным (n — m) переменным могут быть приданы любые, в частности, нулевые значения. Эти переменные называются свободными. Обычно их индексируют x_e, e =(m+1)(1)n. Остальные переменные (их называют базисными), однозначно определяются из решения системы

(здесь x_e, e =(m+1)(1)n). Матрица этой системы неособенная и, следовательно, система имеет единственное решение x_j , j =1(1)m.

Исходный опорный план ЗЛП – вектор, содержащий значения всех переменных задачи как базисных, так и свободных, т.е. этот вектор Х , удовлетворяет ограничениям, но не обеспечивает, как правило, экстремума ЦФ. Общее число опорных планов очевидно равно числу сочетаний из n по m. Оптимальный план можно выявить, перебрав их все. Такой путь громоздок и неприемлем уже при n, m ≈ 10 ÷15.

Алгоритм СМ тоже перебирает опорные планы, но не все, а направленно, т.е. на каждом шаге ЦФ уменьшается. Число шагов имеет тот же порядок, что и число уравнений в ограничениях.

Приведем пояснения некоторым понятиям и терминам, широко используемым в алгоритме решения задач линейного программирования симплексным методом и тесно связанными с ним методами.

Определение. Системой линейных уравнений называют систему следующего вида. Ранг матрицы определяется через миноры r = – 5.

Решение системы уравнений. Решаем относительно переменных x и y, полагаем z = 1. Получаем единственное решение х = –2/5, y = 3/5, z =1. Все другие решения получаются из этого линейно-независимого фундаментального решения: х = –2k/5; y = 3k/5; z = k или х = 2k , y = 3k, z = 5k. Подобные системы возникают при описании ограничений ЗЛП. Существенную роль при решении ЗЛП играют определители подобных систем (Δ = 0, Δ ≠ 0). При однородной системе определитель должен быть равен нулю.

Определение. Симплекс – выпуклый многоугольник в n-мерном пространстве с n + 1 вершинами, не лежащими в одной гиперплоскости. Симплексы выделены в отдельный класс потому, что в n-мерном пространстве n точек всегда лежат в одной гиперплоскости. Другими словами, симплекс – это простейший многоугольник, содержащий некоторый объем n-мерного пространства. В обычном (трехмерном) пространстве симплекс – это тетраэдр; трехмерный объем совпадает с объемом тела. На плоскости симплекс – это треугольник, двумерный объем – площадь; на прямой – симплекс – отрезок, объем – длина отрезка.

Определение. Гиперпространство, гиперплоскость. Гиперпространство многомерного (n-мерного) пространства – это его подпространство размерности (n – 1). Главное свойство гиперпространства – то, что оно «самое большое» подпространство. Иначе говоря, если к базису выбранного гиперпространства добавить еще один линейно независимый вектор, то можно получить базис всего пространства.

Например, для трехмерного пространства гиперпространством является плоскость (любая), проходящая через начало координат. Для двумерного пространства – гиперпространство – это прямая линия, проходящая через нуль.

Гиперплоскость в n-мерном пространстве обобщает наши представления о роли прямой на плоскости и плоскости в пространстве. Например, в n-мерном пространстве через любые n точек можно провести единственную гиперплоскость (как в трехмерном через три точки общего положения, т.е. не лежащие на одной прямой).

Гиперплоскость определяется линейной формой: а₁х₁ + а₂х₂ + … + а_nx_n = k, где коэффициенты (а₁, а₂, …, а_n) представляют собой координаты вектора А.

Гиперплоскость делит пространство (соответствующей размерности) на два полупространства. Все точки каждого из них определяются неравенствами. Например, в случае прямой линии на плоскости: а₁х₁ + а₂х₂ ≥_Z, или а₁х₁ + а₂х₂ >Z _, а₁х₁ + а₂х₂ Литература

Ваулин А. Е. Методы цифровой обработки данных.– СПб.: ВИККИ им. А. Ф. Можайского, 1993.– 106 с.

Гэри М., Джонсон Д. Вычислительные машины и трудно решаемые задачи. М.: Мир, 1982.

Корбут А.А., Финкельштейн Ю. Ю. Дискретное программирование М. Наука. Гл. ред. физ.-мат. лит. 1969.

Макаров И. М. и др. Теория выбора и принятия решений.– М.: Наука, 1982.– 328 с.

Пфанцагль И. Теория измерений. – М.: Наука, 1988.–384 с.

Таха Х. А. Введение в исследование операций. 7-е изд. М.: Изд. дом «Вильямс», 2005.

Фишберн П. С. Теория полезности для принятия решений. – М.: Наука,1978. –352 с.

🐍 Линейное программирование. Практика решения задач оптимизации на Python

Leo Matyushkin

Данная публикация представляет собой сокращенный перевод руководства Мирко Стожилковича Hands-On Linear Programming: Optimization With Python. Для удобства читателей текст перевода также адаптирован в виде Jupyter-блокнота.

Линейное программирование – это набор методов, используемых в математическом программировании, также называемых математической оптимизацией. Эти методы используются для решения систем линейных уравнений и неравенств, перед которыми стоит цель максимизации или минимизации некоторой линейной функции. Линейное программирование используется в научных вычислениях, экономике, технических науках, производстве, транспорте, военном деле, логистике, энергетике и т. д.

Экосистема Python включает несколько мощных инструментов линейного программирования. Из этого руководства вы узнаете:

• что такое линейное программирование и в чем его польза;
• какие инструменты Python подходят для линейного программирования;
• как построить модель и решить задачу линейного программирования на Python.

Что собой представляет линейное программирование

Системы линейных уравнений и неравенств часто имеют множество возможных решений.

Линейное программирование – это набор математических и вычислительных инструментов, позволяющих найти конкретное решение системы, которое соответствует максимуму или минимуму какой-либо другой линейной функции. Линейное программирование – это фундаментальный метод оптимизации, десятилетиями применяемый в областях, требующих большого объема математических вычислений. Эти методы точны, сравнительно быстры и подходят длямножества практических приложений.

Смешанно-целочисленное линейное программирование – это вид линейного программирования, которое фокусируется на обработке задач, где хотя бы одна переменная принимает дискретные целые, а не непрерывно меняющиеся значения.

Целочисленные переменные важны для правильного представления количеств, естественным образом выражаемых целыми числами, таких как число выпущенных самолетов или количество обслуженных клиентов.

Особенно важным видом целочисленных переменных являются бинарные переменные, имеющие лишь значения 0 или 1 , и полезные при принятии решений вида «да»/«нет». Например, следует ли строить завод, включить или выключить машину. Также их можно использовать для имитации логических ограничений.

Смешанно-целочисленное линейное программирование позволяет преодолеть многие ограничения линейного программирования. Можно аппроксимировать нелинейные функции кусочно-линейными, использовать полунепрерывные переменные, логические ограничения модели. Это требовательный к ресурсам инструмент, но достижения в области компьютерного оборудования и программного обеспечения сделали его более доступным.

Линейное программирование на Python

Базовый метод решения задач линейного программирования называется симплекс-методом, другой популярный подход – метод внутренней точки. Задачи смешанного целочисленного линейного программирования решаются с помощью более сложных и ресурсоемких методов, таких как метод ветвей и границ.

Заметим, что почти все широко используемые библиотеки линейного программирования и смешанно-целочисленного линейного программирования написаны на языках Fortran, C или C++, так как линейное программирование требует интенсивной вычислительной работы с матрицами, часто очень большими. Соответствующие инструменты Python – это просто удобные интерфейсы для работы с низкоуровневыми библиотеками – солверами.

В этом руководстве для определения и решения задач линейного программирования мы будем использовать Python-библиотеки SciPy и PuLP.

1. Примеры задач линейного программирования

1.1. Небольшой показательный пример

Рассмотрим следующую задачу максимизации:

Нам нужно найти такие x и y , чтобы выполнялись «красное», «синее» и «желтое» неравенства, а также ограничения x ≥ 0 и y ≥ 0 . При этом решение должно соответствовать максимально возможному значению z .

Независимые переменные, которые нужно найти ( x и y ) называют переменными решения (decision variables). Функция, которую необходимо максимизировать или минимизировать ( z ), – это целевая функция (objective function), функция стоимости (cost function) или просто цель (goal). Неравенства (или уравнения), которым необходимо удовлетворять, называются ограничениями (inequality constraints или equality constraints для обычных уравнений).

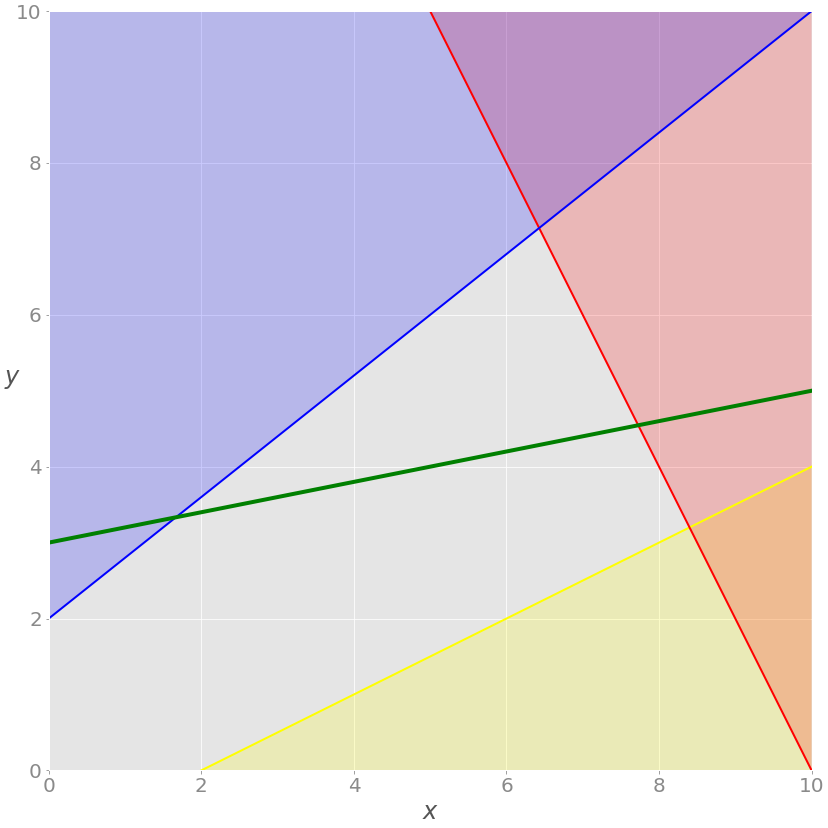
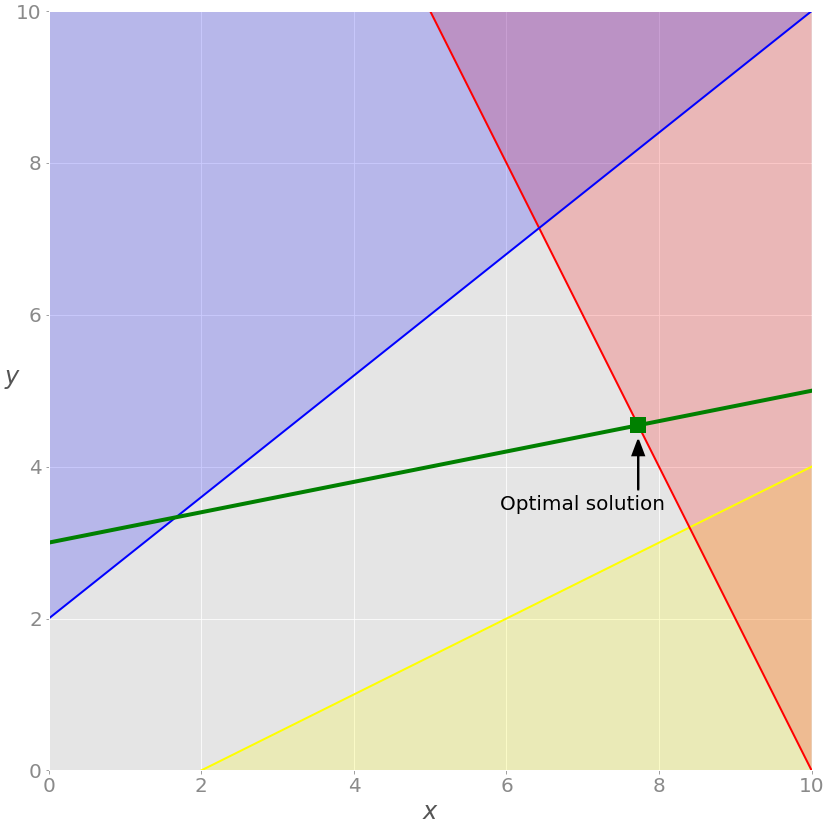
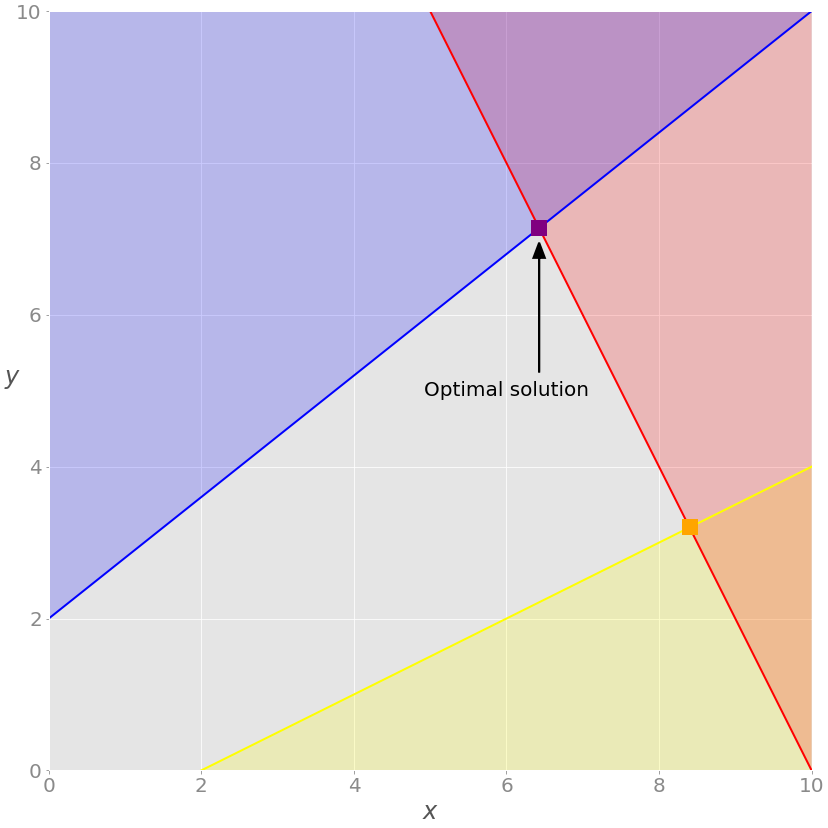
Проблему можно визуализировать следующим образом.

2x + y = 20 , а красная область над ней показывает, где красное неравенство не выполняется. Аналогично синяя линия – это −4x + 5y = 10 , желтая линия – это −x + 2y = −2 , окрашенные области – та часть плоскости, где неравенство не выполняется.» data-src=»https://media.proglib.io/posts/2020/11/26/5a6c3e3ee24ae5a228d7a0ee4ea9fb8a.png» > Красная линия представляет функцию 2x + y = 20 , а красная область над ней показывает, где красное неравенство не выполняется. Аналогично синяя линия – это −4x + 5y = 10 , желтая линия – это −x + 2y = −2 , окрашенные области – та часть плоскости, где неравенство не выполняется.

Каждая точка серой области удовлетворяет всем ограничениям и является потенциальным решением задачи. Эта область называется областью допустимых решений (feasible region), а ее точки – допустимыми решениями (feasible solutions).

Мы хотим максимизировать z . Решение, соответствующее максимальному значению z , называют оптимальным решением.

Обратите внимание, что функция z линейна. Оптимальное решение должно находиться в одной из вершин области допустимых решений. Иногда весь край допустимой области или даже вся область может соответствовать одному и тому же значению z .

Представим, что в задачу введено дополнительное ограничение в виде равенства, окрашенного зеленым:

Его можно визуализировать, добавив соответствующую зеленую прямую:

Теперь область допустимых решений не соответствует всей серой зоне. Это лишь часть зеленой линии, проходящей через серую область от точки пересечения с синей линией до точки пересечения с красной.

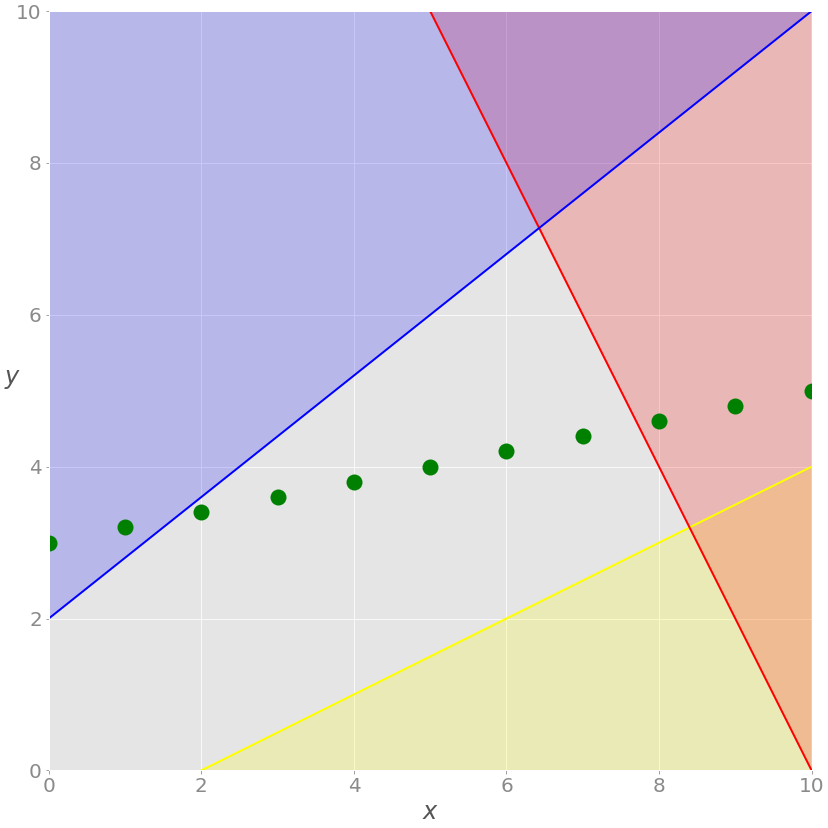
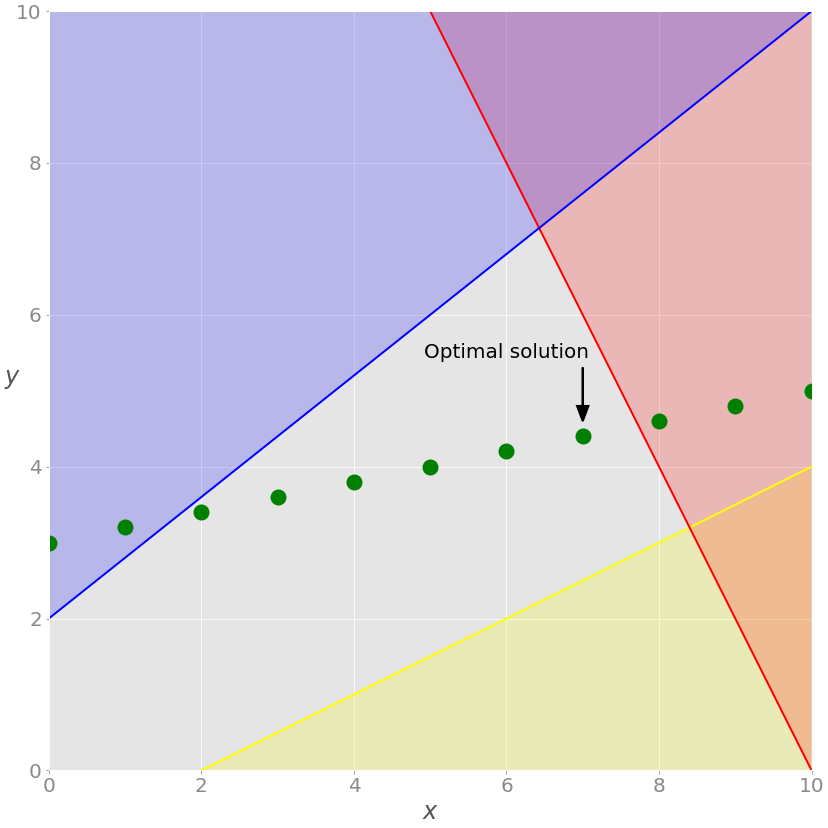
Если добавить требование, что все значения x должны быть целыми числами, то мы получим задачу смешанно-целочисленного линейного программирования, и набор возможных решений снова изменится:

Больше нет зеленой линии – только дискретные точки, где значение x является целым числом. Возможные решения – это зеленые точки на сером фоне.

Эти три примера иллюстрируют задачи линейного программирования – они имеют ограниченные допустимые области решений и конечные решения.

Когда ни одно решение не может удовлетворить все ограничения сразу, задача в рамках линейного программирования неразрешима.

1.2. Задача о распределении ресурсов

В предыдущих разделах мы рассмотрели абстрактную задачу линейного программирования, не связанную с каким-либо реальным приложением. В этом разделе речь пойдет о более практической задачи оптимизации, связанной с распределением ресурсов на производстве.

Предположим, что фабрика производит четыре различных продукта, ежедневное количество первого продукта составляет x_1 , второго продукта – x_2 и т. д. Цель – определить максимальную прибыль ежедневного объема производства для каждого продукта с учетом следующих условий:

1. Прибыль (profit) на единицу продукта составляет 20, 12, 40 и 25 долларов для каждого из четырех продуктов соответственно.
2. Из-за нехватки рабочей силы (manpower) общее количество единиц, производимых в день, не может превышать 50.
3. На каждую единицу 1-го продукта расходуется 3 единицы сырья A. Каждая единица 2-го продукта требует 2 единиц сырья A и 1 единицы сырья B. Каждой единице 3-го продукта требуется 1 единица A и 2 единицы B. Наконец, каждая единица 4-го продукта требует трех единиц. B.
4. Из-за ограничений по транспортировке и хранению фабрика может потреблять до 100 единиц сырья A и 90 единиц B в день.

Математическую модель можно определить так:

Целевая функция (прибыль) определяется в условии 1. Ограничение рабочей силы следует из условия 2. Ограничения на сырье A и B могут быть получены из условий 3 и 4 путем суммирования потребностей в сырье для каждого продукта. Наконец, количество продуктов не может быть отрицательным.

В отличие от предыдущего примера, эту задачу не так удобно визуализировать, потому как она имеет четыре переменных. Однако принципы остаются теми же.

2. Линейное программирование на Python. Практическая реализация

В этом руководстве мы будем использовать для решения описанной выше задачи линейного программирования два пакета Python :

1. SciPy – универсальный пакет для научных вычислений с Python. Его внутренний пакет scipy.optimize можно использовать как для линейной, так и для нелинейной оптимизации.
2. PuLP – API линейного программирования Python для определения задачи и вызова солверов. По умолчанию в качестве солвера используется COIN-OR Branch and Cut Solver (CBC). Еще один отличный солвер с открытым исходным кодом – GNU Linear Programming Kit (GLPK).

2.1. Установка SciPy и PuLP

Чтобы следовать этому руководству, вам необходимо установить SciPy и PuLP.

Возможно, вам потребуется запустить pulptest или sudo pulptest , чтобы включить солверы PuLP, особенно если вы используете Linux или Mac:

2.2. Использование SciPy

В этом разделе мы рассмотрим, как использовать библиотеку SciPy по оптимизации и поиску корней для линейного программирования. Начнём с импорта scipy.optimize.linprog() :

2.3. Решение первого примера c помощью SciPy

Начнём с решения первого (дополненного) примера:

linprog() решает только задачи минимизации (не максимизации) и не допускает ограничений-неравенств со знаком больше или равно ( ≥ ). Чтобы обойти эти проблемы, нам необходимо изменить описание задачи перед запуском оптимизации:

• Вместо максимизации z = x + 2y минимизируем отрицательное значение ( −z = −x − 2y ).
• Вместо знака ≥ мы можем умножить «желтое» неравенство на -1 и получить противоположный знак (ограничения по осям рассмотрим далее).

На следующем шаге определяем входные значения:

Мы поместили значения из системы в соответствующие списки:

• obj содержит коэффициенты целевой функции,
• lhs_ineq и rhs_ineq содержат коэффициенты из ограничений-неравенств,
• lhs_eq и rhs_eq содержат коэффициенты из ограничивающего уравнения.

Следующим шагом является определение границ каждой переменной. В данном случае они находятся между нулем и положительной бесконечностью:

Однако эти границы совпадают с установленными по умолчанию в linprog() .

Наконец, пришло время оптимизировать и решить интересующую нас проблему:

Параметр c относится к коэффициентам из целевой функции. A_ub и b_ub соответственно связаны с коэффициентами из левой и правой частей ограничений-неравенств. Точно так же A_eq и b_eq относятся к ограничениям уравнений. Параметр bounds служит для указания нижней и верхней границ переменных решения.

Параметр method определяет используемый алгоритм линейного программирования. Доступны три варианта:

• по умолчанию используется метод внутренней точки: method = «inner-point»,
• измененный двухфазный симплекс-метод method=»revised simplex»,
• симплекс-метод method=»simplex»

linprog() возвращает структуру данных со следующими атрибутами:

• .con – остатки ограничения-равенства;
• .fun – оптимальное значение целевой функции (если найдено);
• .message – словесный статус решения;
• .nit – количество итераций, необходимых для завершения расчета;
• .slack – значения так называемых дополнительных переменных – разниц между значениями левой и правой сторонами ограничений;
• .status – целое число от 0 до 4, отражающих результат решения: например, 0, когда было найдено оптимальное решение;
• .success – логическое значение, показывающее, найдено ли оптимальное решение;
• .x – массив NumPy, содержащий оптимальные значения переменных решения.

Доступ к атрибутам можно получить по отдельности:

Графически результат можно отобразить следующим образом.

Вначале наша задача органичивалась только неравенствами. Если удалить параметры зеленого уравнения A_eq и b_eq из вызова linprog() , получим следующий результат:

2.4. Решение задачи о производстве с помощью SciPy

Рассмотрим теперь решение второй задачи – о продуктах, рабочей силе и используемом сырье.

Как и в предыдущем примере, нам нужно извлечь необходимые векторы и матрицу из задачи, передать их в качестве аргументов в linprog() :

Максимальная прибыль составляет 1900 и соответствует x_1 = 5 и x_3 = 45 . В данных условиях производить второй и четвертый продукты невыгодно. Результат позволяет сделать несколько интересных выводов:

1. Третий продукт приносит наибольшую прибыль.
2. Первая дополнительная переменная ( slack ) равна 0. Это означает, что равны значения левой и правой сторон ограничения для рабочей силы. Завод производит 50 единиц в день, и это его полная мощность.
3. Вторая дополнительная переменная равна 40: фабрика потребляет 60 единиц сырья A (15 единиц для первого продукта и 45 для третьего) из возможных 100 единиц.
4. Третья дополнительная переменная равен 0: фабрика потребляет все 90 единиц сырья B. При этом все это количество потребляется для производства третьего продукта. Вот почему фабрика вообще не может производить второй или четвертый товар и не может произвести более 45 единиц третьего товара. Cырья B просто не хватает.

Возможности линейного программирования SciPy полезны в основном для небольших задач. Для более крупных и сложных проблем разумно использовать другие библиотеки:

• SciPy не поддерживает работу с целочисленными переменными решения.
• SciPy не подразумевает запуск внешних солверов.
• SciPy не предоставляет классы или функции для построения моделей. Определять массивы и матрицы вручную для крупных задач слишком утомительно.
• Также вручную приходится переопределять задачи, как мы это сделали выше.

2.5. Решение первой задачи на линейное программирование с помощью PuLP

Итак, PuLP имеет более удобный API линейного программирования, чем SciPy. Начнем с импорта.

Первый шаг – инициализировать экземпляр LpProblem для описания модели:

Параметр sense определяет, решаем ли мы задачу минимизации (параметр LpMinimize или 1 , установлен по умолчанию) или максимизации ( LpMaximize или -1 ).

Создав модель, мы можем определить переменные решения как экземпляры класса LpVariable :

Значения границ по умолчанию – отрицательная и положительная бесконечности, поэтому в нашем случае необходимо указать нижнюю границу ( lowBound = 0 ).

Необязательный параметр cat определяет категорию переменной решения. При работе с непрерывными переменными можно использовать значение по умолчанию «Continuous» .

Переменные x и y теперь можно использовать для создания других PuLP-объектов, представляющих линейные выражения и ограничения:

Построив линейную комбинацию нескольких переменных решения, мы получаем экземпляр pulp.LpAffineExpression , представляющий линейное выражение. Выражения можно комбинировать с операторами == , и >= и получать экземпляры pulp.LpConstraint – линейные ограничения вашей модели.

Опишем теперь ограничения. В отличие от SciPy, с PuLP не нужно создавать списки и матрицы. Просто записываем выражения Python и добавляем в модель с помощью оператора += :

LpProblem позволяет добавлять ограничения в модель, определяя их как кортежи. Первый элемент кортежа – экземпляр LpConstraint , второй – его удобочитаемое имя.

Аналогично описывается целевая функция:

Теперь можно посмотреть полное определение модели:

Строковое представление модели содержит все соответствующие данные: цель, переменные, ограничения и их имена.

Теперь мы готовы решить задачу. Достаточно лишь вызвать метод .solve() для объекта модели.

Метод .solve() вызывает базовый солвер, изменяет объект модели и возвращает целочисленный статус решения, равный 1, если найден оптимум. Остальные коды состояний описаны в документации.

Результаты оптимизации доступны в виде атрибутов модели:

model.objective содержит значение целевой функции, model.constraints – значения дополнительных переменных, а объекты x и y имеют оптимальные значения переменных решения.

Результаты получились примерно такие же, как у SciPy.

Чтобы получить смешанно-целочисленное решение, достаточно обозначить это при помощи параметра cat :

Теперь x – целое число, как указано в модели. Этот факт меняет решение. Покажем это на графике:

Как видите, оптимальным решением является крайняя правая зеленая точка на сером фоне. Это решение с наибольшими значениями как x , так и y , дающее максимальное значение целевой функции.

2.6. Решение задачи о производстве с помощью PuLP

Подход к определению и решению второй задачи такой же, как и в предыдущем примере:

Как видите, решение согласуется с тем, что мы молучили с помощью SciPy. Наиболее выгодное решение – производить в день 5 единиц первого продукта и 45 единиц третьего.

Давайте сделаем задачу более интересной. Допустим, из-за проблем с оборудованием, фабрика не может производить первую и третью продукцию параллельно. Какое решение наиболее выгодно в этом случае?

Теперь у нас есть еще одно логическое ограничение: если x_1 положительно, то x_3 должно равняться нулю, и наоборот. Здесь пригодятся бинарные переменные решения. Введем две переменные y_1 и y_3 , которые будут обозначать, генерируются ли вообще первый или третий продукты:

При таких условиях оказывается, что оптимальный подход – исключить первый продукт вовсе и производить только третий.

Заключение

Теперь вы в общих чертах представляете, с какими задачами имеет дело линейное программирование и как использовать Python для решения подобных задач.

Теперь – после прохождения этого руководства – вы умеете:

• определить модель, которая описывает задачу в SciPy и PuLP;
• создать программу Python для оптимизационной задачи;
• запустить программу оптимизации, чтобы найти решение задачи;
• получить результат оптимизации.

Если вы хотите узнать больше о линейном программировании, вот несколько отправных точек, с которых можно начать:

Следите за нашими тегами Python и Математика!