Кривые второго порядка — определение и построение с примерами решения
Содержание:
Геометрической фигурой или просто фигурой на плоскости называется множество точек. Задать фигуру — значит указать, из каких точек плоскости она состоит. Одним из важных способов задания фигуры на плоскости является ее задание при помощи уравнений с двумя неизвестными. Произвольное уравнение с двумя неизвестными х и у записывается в виде
- Если точка М(а,Ь) принадлежит фигуре Ф, то координаты (а,Ь) являются решениями уравнения
- если пара чисел (c,d) является решением уравнения F(x,y) = 0, то точка N(c,d) принадлежит фигуре Ф.
Это определение в более компактной записи выглядит следующим образом. Уравнение 

Из определения уравнения фигуры следует, что фигура Ф состоит только из тех точек плоскости, координаты которых являются решениями уравнения 
Возможны два вида задач:
- дано уравнение
и надо построить фигуру Ф, уравнением которой является
;
- дана фигура Ф и надо найти уравнение этой фигуры.
Первая задача сводится к построению графика уравнения 
Для решения второй задачи, как следует из определения уравнения фигуры, достаточно:
- Задать фигуру геометрически, т.е. сформулировать условие, которому удовлетворяют только точки фигуры (довольно часто определение фигуры содержит такое условие);
- Записать в координатах условие, сформулированное в первом пункте.
Эллипс
Эллипсом называется линия, состоящая из всех точек плоскости, для каждой из которых сумма расстояний до двух данных точек 

Точки 
Если а =Ь, то уравнение (7.3) можно переписать в виде:

Это уравнение окружности с центром в начале координат. Эллипс (3) можно получить из окружности (4) сжатием плоскости к оси Ох. Пусть на плоскости выбрана прямоугольная система координат Оху. Тогда преобразование, переводящее произвольную точку М(х,у) в точку 

Число 


Фокальными радиусами точки М эллипса называются отрезки прямых, соединяющие эту точку с фокусами 







Директрисы обладают следующим свойством: отношение расстояния г любой точки эллипса от фокуса к ее расстоянию d до соответствующей директрисы есть величина постоянная, равная эксцентриситету, т.е.
Гипербола
Гиперболой называется линия, состоящая из всех точек плоскости, модуль разности расстояний от которых до двух данных точек 

Точки 



Тогда 




Уравнение (9.4.1)- каноническое уравнение параболы. Уравнения 
Легко показать, что уравнение 

и сделаем параллельный перенос по формулам
В новых координатах преобразуемое уравнение примет вид: 

Пример:
Пусть заданы точка F и прямая у =-1 (рис. 9.8). Множество точек Р(х, y) для которых расстояние |PF| равно расстоянию




Кривые второго порядка на плоскости
Кривой второго порядка называется фигура на плоскости, задаваемая в прямоугольной системе координат уравнением второй степени относительно переменных х и у:
где коэффициенты А, В и С не равны одновременно нулю
Любая кривая второго порядка на плоскости принадлежит к одному из типов: эллипс, гипербола, парабола, две пересекающиеся прямые, 2 параллельные прямые, прямая, точка, пустое множество.
Кривая второго порядка принадлежит эллиптическому типу, если коэффициент В равен нулю: В=0, а коэффициенты А и С имеют одинаковые знаки: АС>0.
Кривая второго порядка принадлежит гиперболическому типу, если коэффициент В равен нулю: В=0, а коэффициенты А и С имеют противоположные знаки: АС 2с. Точка М(х,у) принадлежит эллипсу тогда и только тогда, когда ее координаты удовлетворяют уравнению

Число а называют большей полуосью эллипса, число 
шей полуосью эллипса, 2а и 2b — соответственно большей и меньшей осями эллипса. Точки 

Координатные оси являются осями симметрии эллипса, а начало координат — его центром симметрии. Центр симметрии эллипса называется центром эллипса.
Замечание. Каноническое уравнение эллипса можно рассматривать и в случае b>а. Оно определяет эллипс с большей полуосью b, фокусы которого лежат на оси Оу.
В случае а=b каноническое уравнение эллипса принимает вид 
Эксцентриситетом эллипса называется отношение фокусного расстояния к длине большей оси.
Так, в случае а>b эксцентриситет эллипса выражается формулой:
Эксцентриситет изменяется от нуля до единицы 

Пример:
Показать, что уравнение
является уравнением эллипса. Найти его центр, полуоси, вершины, фокусы и эксцентриситет. Построить кривую.
Решение:
Дополняя члены, содержащие х и у соответственно, до полных квадратов, приведем данное уравнение к каноническому виду:


Найдем эксцентриситет эллипса:
Для вычисления вершин и фокусов удобно пользовать новой прямоугольной системой координат, начало которой находится в точке 

В новой системе координат координаты 
Переходя к старым координатам, получим:
Построим график эллипса.

Гиперболой называется множество всех точек плоскости, для которых модуль разности расстояний до двух данных точек, называемых фокусами, есть величина постоянная, меньшая расстояния между фокусами.
Так же, как и для эллипса, геометрическое свойство точек гиперболы выразим аналитически. Расстояние между фокусами назовем фокусным расстоянием и обозначим через 2с. Постоянную величину обозначим через 2а: 2а
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
ОБЩЕЕ УРАВНЕНИЕ ЛИНИЙ ВТОРОГО ПОРЯДКА
Линии второго порядка
1. Основные понятия.
6. Общее уравнение линий второго порядка.
ОСНОВНЫЕ ПОНЯТИЯ
Рассмотрим линии, определяемые уравнениями второй степени относительно текущих координат

Коэффициенты уравнения – действительные числа, но, по крайней мере, одно из чисел 
ОКРУЖНОСТЬ
Простейшей кривой второго порядка является окружность.
Определение. Окружностью радиуса R с центром в точке 


Каноническое уравнение окружности 
Эллипс
Определение. Эллипсом называется множество всех точек плоскости, сумма расстояний от каждой из которых до двух данных точек этой плоскости, называемых фокусами, есть величина постоянная и большая, чем расстояние между фокусами.
Каноническое уравнение эллипса 

с – половина расстояния между фокусами; a – большая полуось; b – малая полуось.



Теорема. Фокусное расстояние и полуоси эллипса связаны соотношением:
Определение.Характеристикой эллипса, показывающей меру его вытянутости, является эксцентриситет – величина, определяемая отношением: 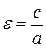
Замечание. Для эллипса 
Определение.Прямые 
Теорема. Если 
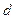


Замечание. Если a = b, то c = 0, а значит, фокусы сливаются, и эллипс превращается в окружность.
Если же 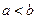



Пример. Составьте уравнение эллипса, если его фокусы F1(0; 0), F2(1; 1), а большая ось равна 2.
Уравнение эллипса имеет вид: 
Расстояние между фокусами: 2c = 
a 2 – b 2 = c 2 = 
По условию большая ось равна 2, то есть 2а = 2, откуда получаем, что
а = 1, b = 
Тогда искомое уравнение эллипса имеет вид: 
Гипербола
Определение. Гиперболойназывается линия, для всех точек которой модуль разности расстояний от двух данных точек, называемых фокусами, есть величина постоянная и меньшая, чем расстояние между фокусами.
Каноническое уравнение гиперболы 

Теорема. Фокусное расстояние и полуоси гиперболы связаны соотношением:
Ось 2а называется действительной осью гиперболы.
Ось 2b называется мнимой осью гиперболы.
Прямоугольник со сторонами 2а и2b называется основным прямоугольником гиперболы.
Гипербола имеет две асимптоты, уравнения которых
Замечание.Для гиперболы эксцентриситет 
Определение. Две прямые, перпендикулярные действительной оси гиперболы и расположенные симметрично относительно центра на расстоянии a/ε от него, называются директрисами гиперболы. Их уравнения: 
Определение. Гипербола называется равносторонней, если ее полуоси равны ( 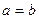
Ее каноническое уравнение 
Определение. Эксцентриситетом гиперболы называется отношение расстояние между фокусами к величине действительной оси гиперболы, обозначается 

Кривая, определяемая уравнением 



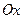
Гиперболы 

Пример. Составьте уравнение гиперболы, если ее эксцентриситет равен 2, а фокусы совпадают с фокусами эллипса, заданного уравнением
Найдем фокусное расстояние для эллипса:
Тогда искомое уравнение гиперболы 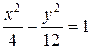
Парабола
Определение. Параболой называется множество всех точек плоскости, каждая из которых одинаково удалена от данной точки, называемой фокусом, и от данной прямой, называемой директрисой и не проходящей через фокус.
Каноническое уравнение параболы y 2 = 2px .
Конспекты :»Кривые второго порядка»
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
1. Окружность и ее уравнение
Кривая второго порядка – линия на плоскости, задаваемая уравнением: Ах 2 +2Вху+Су 2 +2Dx+2Ey+F=0 , где коэффициенты А, В, С, D, E, F – любые действительные числа при условии, что А, В, С одновременно не равны нулю.
Выделяют следующие кривые второго порядка:
Окружностью называется множество точек плоскости, равноудаленных от одной точки, называемой центром.
Пусть центром окружности является точка О ( a;b ), а расстояние до любой точки М ( x;y ) окружности равно R (рис.1). Составим уравнение окружности.
Расстояние от точки М до центра окружности можно найти, пользуясь формулой расстояния между точками:
Подставив в это выражение координаты точек М и О ,получим:
Поскольку расстояние ОМ равно радиусу R , следовательно, R = .
Возведём обе части уравнения в квадрат:
Это уравнение называется каноническим уравнением окружности с центром О ( a ; b ) и радиусом R .
Если центр окружности совпадает с началом координат, то уравнение окружности имеет вид: x 2 + y 2 = R 2 .
Пример 1 Составьте уравнение окружности с центром О (3; -2) и радиусом r = 5.
Решение: Подставив a =3, b =-2 и r = 5 в каноническое уравнение окружности 

Пример 2 Запишите уравнение окружности с центром в точке М(-3;1), которая проходит через точку К(-1;5)
Подставим значения в уравнение окружности
Составьте уравнение окружности
А. О(-2;1) R =4 Б. М ( 1; -4) , R = 2; В. М ( 0; -5) , R = 3; Г. О (-3;2), R =4.
Составьте уравнение окружности с центром в точке М (1; -4), проходящей через точку А(0; 3).
Определите по уравнению окружности координаты ее центра и радиус :
А) (Х+2)² + ( У – 5)² = 49 Б) (Х+7)² + ( У + 1)² = 36
В) (Х- 6)² + ( У + 15)² = 81 Г) Х ² + ( У -9)² = 2
Эллипс и его уравнение
Эллипсом называется множество точек на плоскости, сумма расстояний от каждой из которых до двух заданных точек (называемых фокусами ) есть величина постоянная, большая, чем расстояние между фокусами.
Фокусы эллипса принято обозначат буквами F 1 и F 2 , расстояние между фокусами – через 2с , сумму расстояний от любой точки эллипса до фокусов- через 2а (2а).
Каноническое уравнение эллипса имеет вид:
Где a , b , c – связаннымежду собой равенством или .
Рассмотрим два основных случая расположения эллипса относительно осей координат. Эти случаи представлены в следующей таблице:
Эксцентриситетом эллипса называется отношение расстояния между фокусами к длине большей оси. Эксцентриситет обозначается буквой .
Так как по определению 2 a , то эксцентриситет всегда выражается правильной дробью, те 0
Если то эллипс сильно вытянут;
если же то эллипс имеет более круглую форму.
если то эллипс вырождается в окружность.
№ 1Найти координаты фокусов, длины осей и эксцентриситет эллипса, заданного уравнением
Находим фокусы эллипса: а 2 =16 b 2 =32
Откуда а=4; b =или 4.
Так как b , то фокусы эллипса расположены на оси ординат
Находим длины осей:
Найти координаты фокусов, длины осей и эксцентриситет эллипса, заданного уравнением:
Гипербола и ее уравнение
Гиперболой называется множество точек плоскости, разность расстояний от каждой из которых до двух заданных точек (фокусов) есть величина постоянная.
Эта постоянная величина положительна и меньше расстояния меду фокусами.
Фокусы гиперболы принято обозначат буквами F 1 и F 2 , расстояние между фокусами – через 2с , постоянную разность между расстояниями от любой точки гиперболы до ее фокусов — через 2а (2а).
Каноническое уравнение гиперболы имеет вид:
Где a , b , c – связанны между собой равенством .
Рассмотрим два основных случая расположения гиперболы относительно осей координат. Эти случаи представлены в следующей таблице:
Эксцентриситетом гиперболы называется отношение расстояние между фокусами к длине действительной оси.
Так как по определению 2а
Прямые называются асимптотами ; их уравнения имеет вид
№ 1 Найти координаты фокусов, длины осей, эксцентриситет и уравнения асимптот, если гипербола задана уравнением
Приведем уравнение к каноническому виду, т.е. разделим обе его части на 400
Самостоятельно: Найти координаты фокусов, длины осей, эксцентриситет и уравнения асимптот, если гипербола задана уравнением .
Парабола и ее уравнение
Параболой называется множество точек на плоскости, равноудаленных от заданной точки ( называемой фокусом ) и данной прямой ( называемой директрисой ).
Фокус параболы принято обозначать буквой F , директрису буквой d , расстояние от фокуса до директрисы — буквой p ( p ). Рассмотрим основные случаи расположения параболы относительно осей координат.
Каноническое уравнение параболы, фокус которой расположен на оси абсцисс (рис.61,62), имеет вид
Эти два случая представлены в следующей таблице:
Каноническое уравнение параболы, фокус которой расположен на оси ординат (рис.63,64), имеет вид
Эти два случая представлены в следующей таблице:

№1 Найти координаты фокуса и уравнение директрисы параболы, заданной уравнением
№ 2 Найти каноническое уравнение параболы и уравнение ее директрисы, если известно, что вершина параболы лежит в начале координат, а фокус имеет координаты (0;-3).
Фокус параболы отрицателен, т.к. его координаты (0;-3) следовательно, уравнение параболы имеет вид (ветви параболы направлены вниз ).
Составляем уравнение параболы:
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
- Сейчас обучается 932 человека из 80 регионов
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
- Сейчас обучается 682 человека из 75 регионов
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Сейчас обучается 308 человек из 69 регионов
Ищем педагогов в команду «Инфоурок»
Дистанционные курсы для педагогов
«Взбодрись! Нейрогимнастика для успешной учёбы и комфортной жизни»
Свидетельство и скидка на обучение каждому участнику
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 575 225 материалов в базе
Самые массовые международные дистанционные
Школьные Инфоконкурсы 2022
33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»
Другие материалы
- 17.12.2018
- 254
- 0
- 17.12.2018
- 215
- 0
- 17.12.2018
- 216
- 0
- 17.12.2018
- 882
- 19
- 17.12.2018
- 385
- 6
- 17.12.2018
- 305
- 9
- 17.12.2018
- 684
- 13
- 17.12.2018
- 457
- 2
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Добавить в избранное
- 17.12.2018 5657
- DOCX 162.3 кбайт
- 89 скачиваний
- Оцените материал:
Настоящий материал опубликован пользователем Фадина Кристина Валерьевна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала
- На сайте: 5 лет и 7 месяцев
- Подписчики: 1
- Всего просмотров: 60703
- Всего материалов: 63
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Дистанционные курсы
для педагогов
663 курса от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
В Курганской области дистанционный режим для школьников продлили до конца февраля
Время чтения: 1 минута
ЕГЭ в 2022 году будут сдавать почти 737 тыс. человек
Время чтения: 2 минуты
Полный перевод школ на дистанционное обучение не планируется
Время чтения: 1 минута
Приемная кампания в вузах начнется 20 июня
Время чтения: 1 минута
Тринадцатилетняя школьница из Индии разработала приложение против буллинга
Время чтения: 1 минута
Минобрнауки создаст для вузов рекомендации по поддержке молодых семей
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
http://poisk-ru.ru/s7872t3.html
http://infourok.ru/konspekti-krivie-vtorogo-poryadka-3454036.html






























