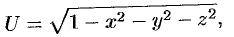Уравнение линии уровня скалярного поля

Скалярное поле. Векторное поле. Основные понятия и задачи

Понятие поля в математике

Теория поля является разделом математики, однако понятие поля лежит в основе многих представлений современной физики. В общем случае говорят, что в пространстве задано поле некоторой величины u , если в каждой точке пространства (или некоторой его части) определено значение этой величины. Так, например, при изучении потока газа приходится исследовать несколько полей: температурное поле (в каждой точке температура имеет определённое значение), поле давлений, поле скоростей и другие поля.

Поле величины u называется стационарным, (или установившимся), если u не зависит от времени t . В противном случае поле называется нестационарным (или неустановившимся). Таким образом, величина u есть функция точки M и времени t .

В задачах физики чаще всего приходится иметь дело со скалярными и векторными величинами. В соответствии с этим различают два вида полей: скалярные и векторные.

Скалярное поле: определение, поверхности уровня и линии уровня

Пусть D — некоторая область на плоскости или в пространстве.

Определение скалярного поля. Если в области D каждой точке M(x,y,z) пространства или точке M(x,y) плоскости в каждый момент времени t по определённому закону ставится в соответствие значение скалярной величины u , то функция u(x,y,z,t) в случае пространства или u(x,y,t) в случае плоскости называется скалярным полем.

Понятия скалярного поля и функции, определённой в области D , совпадают.

Примером скалярного поля может служить поле температур воздуха в некотором помещении, если температуру рассматривать как функцию точки. В точках, расположенных ближе к источнику тепла, температура выше, чем в точках, расположенных дальше от источника тепла. Можно привести и такие примеры, как поле освещённости, поле плотности массы и тому подобные.

Для получения более полного представления о скалярном поле используется его графическое изображение — поверхности уровня в пространстве и линии уровня на плоскости.

Линии уровня широко используются при составлении топографических и метеорологических карт. На топографических картах линия уровня — линия, в точках которой отмечена одна и та же высота над уровнем моря. На метеорологических картах строят два вида линий уровня — изотермы (линии одинаковой температуры) и изобары (линии одинакового давления).

Определение. Поверхностью уровня скалярного поля называется множество всех тех точек пространства, в которых скалярное поле постоянно.

Уравнение поверхности уровня скалярного поля u(x,y,z) :

При постоянном изменении значения C поверхности уровня заполняют всю область пространства. Если поверхности уровня размещены плотно, скалярное поле изменяется быстро. Если же поверхности уровня расположены редко, скалярное поле изменяется медленно.

Определение. Линией уровня скалярного поля называется множество всех тех точек на плоскости, в которых скалярное поле постоянно.

Уравнение линии уровня скалярного поля u(x,y) :

Пример 1. Определить поверхности уровня скалярного поля и их вид.

Решение. Уравнением поверхностей уровня данного скалярного поля является

.

Поверхностями уровня являются конусы с вершиной в начале координат и осью вращения Oy . Так как по области определения , то одновременно не может быть x = 0 и z = 0 . Поэтому следует исключить вершину конусов.

Пример 2. Определить линии уровня скалярного поля и их вид.

Решение. Уравнением линий уровня данного скалярного поля является

.

Из этого уравнения выразим «игрек»:

.

Так как arcsinC — также константа, обозначим её C 1 . Тогда

Графиками этих линий являются параболы с вершиной в точках и ветвями вниз. На рисунке изображены линии уровня в трёх случаях: C 1 = 1 — красная линия, C 1 = 2 — зелёная линия, C 1 = 3 — синяя линия.

Векторное поле: определение, векторные линии

Понятие векторного поля во многом аналогично понятию скалярного поля.

Определение векторного поля. Если в некоторой области пространства каждой точке M по определённому закону ставится в соответствие вектор , то векторная функция называется полем вектора или векторным полем.

Таким образом, векторным полем является векторная функция точки пространства

Примерами векторного поля являются поля скорости и ускорения в текущей жидкости или газе, поле силы гравитации, поле интенсивности электростатического поля и тому подобные. Вообще, примером векторного поля может служить поле сил любой природы.

Мы будем рассматривать только стационарные векторные поля, то есть поля, не зависящие от времени.

Проекции вектора , соответствующего точке M , на координатные оси обозначим P = P(x,y,z) , Q = Q(x,y,z) , R = R(x,y,z) . Тогда векторное поле сможем задать через компоненты:

.

Таким образом, векторное поле можно определить тремя скалярными функциями P , Q , R . Пусть эти функции и их частные производные по переменным x,y,z являются непрерывными функциями.

Определение. Векторной линией называется линия, направление которой в каждой точке касательной совпадает с направлением вектора поля в этой точке (рисунок ниже).

Векторные линии поля силы обычно называют линиями силы, векторные линии поля скоростей потока жидкости или газа — векторами потока. У стационарного потока жидкости линии потока совпадают с траекториями частиц жидкости.

Уравнения векторных линий можно найти, решив систему дифференциальных уравнений

.

Пример 3. Найти линии вектора поля .

Решение. Так как , , , получаем систему дифференциальных уравнений

.

Из первого равенства получаем

где . Из последнего равенства следует . Таким образом, получаем

И получаем уравнения векторных линий данного векторного поля:

Поверхности и линии уровня скалярного поля

Поверхности и линии уровня

Рассмотрим скалярное поле, задаваемое функцией 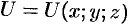. Для наглядного представления скалярного поля используют поверхности и линии уровня.

Поверхностью уровня скалярного поля называется геометрическое место точек, в которых функция 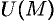принимает постоянное значение, т. е.

Давая в уравнении (70.1) величине с различные значения, получим различные поверхности уровня, которые в совокупности как бы расслаивают поле. Через каждую точку поля проходит только одна поверхность уровня. Ее уравнение можно найти путем подстановки координат точки в уравнение (70.1).

Для скалярного поля, образованного функцией

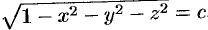
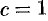
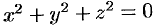
поверхностями уровня является множество концентрических сфер с центрами в начале координат: . В частности, при получим , т. е. сфера стягивается в точку.

Для равномерно раскаленной нити поверхности уровня температурного поля (изотермические поверхности) представляют собой, круговые цилиндры, общей осью которых служит нить.

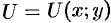
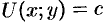
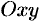
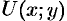
В случае плоского поля равенство представляет собой уравнение линии уровня поля, т. е. линия уровня — это линия на плоскости , в точках которой функция сохраняет постоянное значение.

В метеорологии, например, сети изобар и изотерм (линии одинаковых средних давлений и одинаковых средних температур) являются линиями уровня и представляют собой функции координат точек местности.

Линии уровня применяются в математике при исследовании поверхностей методом сечений (см. п. 12.9).

На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:

Другие темы по высшей математике возможно вам они будут полезны:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Электронная библиотека

Полем называется область пространства, каждой точке Р которой поставлена в однозначное соответствие некоторая величина Q(p).

Если величина Q(p) является физической, то поле называется физическим. В зависимости от природы функции Q(p), поля разделяются на скалярные и векторные. Примерами скалярных физических полей могут быть поля температуры, атмосферного давления, плотности воздуха, электрического потенциала, массы и т.д. К векторным величинам относятся: поля силы тяжести, скорости частиц текущей жидкости (газа), сдвига точек упругого тела, магнитной индукции и др.

Если функция Q(p) не изменяется с течением времени, то поле называется стационарным или установившимся, в противном случае – нестационарным.

Для получения общих результатов, справедливых для любых конкретных физических полей, всякому полю ставится в соответствие его математическая модель. Математическая теория поля изучает свойства векторных и скалярных полей, которые выявляются практическими задачами из физики, электротехники, математики и других наук.

Для успешного овладения теорией поля необходим математический аппарат, в который входит векторная алгебра и векторный анализ, элементы дифференциального и интегрального исчисления. Отметим, что в перспективе обобщением теории скалярных и векторных полей является теория тензорных полей, которая играют важную роль в теории упругости, теории относительности и др.

Для задания скалярного поля надо задать скалярную функцию . Введем понятие поверхности (линии) равного уровня скалярного поля.

Определение. Поверхностью равного уровня скалярного поля называется такая поверхность, на которой функция имеет постоянное значение.

Уравнение поверхности уровня:

где С – постоянная. Если функция , то говорят о линии равного уровня: .

При различных значениях С получаем семейство поверхностей (линий) уровня. Примерами поверхностей уровня являются поверхности: равных температур в некотором теле; равного потенциала V в электрическом поле .

Совокупность поверхностей (линий) уровня дает наглядное представление конкретного поля, что облегчает его изучение.

Найти поверхность уровня поля , проходящую через точку .

Решение. Уравнение поверхности уровня: U = C:

Очевидно, . Поверхностями уровня служит семейство сфер с центром в начале координат. Чтобы выбрать нужную сферу, проходящую через , требуется подставить координаты этой точки в уравнение поверхностей уровня:

Уравнение искомой поверхности уровня:

описывает сферу радиуса R = 3 с центром в начале координат.

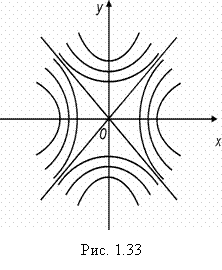
Найти линии уровня поля .

При С > 0 линии уровня есть равнобочные гиперболы с вершинами на оси Ох; при С = 0 – прямые – асимптоты этих гипербол (сопряженных) (рис. 1.33).

Понятие скалярного поля тесно связано с важным понятием производной скалярной функции по заданному направлению (в математическом анализе этого не было).

Теорема: если функция дифференцируема в точке Р, то производная в точке Р по любому направлению существует и равна (обозначается ):

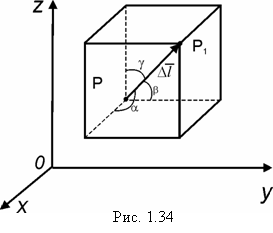
Доказательство. Как известно из математического анализа [6], если функция дифференцируема, то её приращение (рис.

Разделим на обе части последнего равенства, получим:

Переходя к пределу при , и учитывая, что

получим формулу (1.91). Если , то поле возрастает; при – убывает и – дает скорость изменения поля в направлении .

Найти производную от функции по направлению от точки Р(1; 1; 1) к точке Р₁(2; 3; 4).

Формула (1.91) ставит задачу: найти то направление, которое доставляет максимальное значение для . Оказывается, такое направление дается понятием градиента скалярного поля.

Определение. Градиентом скалярного поля (обозначается grad U) называется вектор, проекции которого на оси декартовой системы координат есть , , , т.е.

Вывод: градиент скалярного поля есть вектор.

Имеется связь между производной по направлению и градиентом (рис. 1.35).

Найдем скалярное произведение :

.

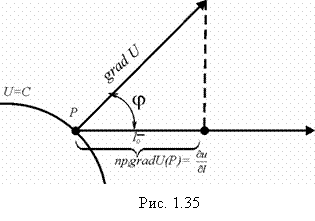
Таким образом, левая часть полученного равенства есть .

При изменении будет меняться и . Очевидно, эта проекция будет максимальной, когда направление совпадает с . Учитывая физический смысл производной по направлению и формулу (1.94) убеждаемся в том, что: вектор grad U по величине и направлению есть наибольшая скорость возрастания . В этом состоит физический смысл градиента. Это широко используется в практике.

Покажем, что направлен по нормали к поверхности (линии) уровня скалярного поля , проходящей через точку Р.

Уравнение поверхности уровня: . Уравнение нормали к поверхности уровня:

где X, Y, Z – текущие координаты нормали; x, y, z – координаты поверхности, в которой проведена нормаль. Видим, что проекции направляющего вектора нормали те же, что и градиента.

Найти наибольшую скорость возрастания скалярного поля в точке Р(1; 2; 3).

Решение. Согласно (1.92) имеем:

Поверхность уровня поля U, проходящая через точку Р(1; 2; 3) – сфера: . Наибольшая скорость возрастания функции U будет в направлении радиуса этой сферы, проходящего через данную точку Р(1; 2; 3).

Срочно?
Закажи у профессионала, через форму заявки
8 (800) 100-77-13 с 7.00 до 22.00