Уравнение линии второго порядка привести к каноническому

Приведение кривой второго порядка к каноническому виду

Пример №1 . Привести уравнение второго порядка к каноническому виду с помощью поворота и параллельного переноса осей координат. Построить кривую.

Пример №2 . Выполнив последовательно преобразования координат: поворот, а затем параллельный перенос координатных осей, преобразовать к каноническому виду уравнение кривой второго порядка и построить ее в исходной системе координат, а также найти параметры кривой.

Алгоритм перехода кривой второго порядка к каноническому виду

Пример №1 . 4y=-6-sqrt(4x-x 2 )
sqrt(4x-x 2 ) = -(4y+6)
Возведем в квадрат
4x-x 2 = (4y+6) 2
Раскрывая скобки, получаем:
16y 2 +48y + 36 +x 2 -4x = 0

Далее решается калькулятором. Если самостоятельно решать, то получим:
4x-x 2 = (4y+6) 2
-(x 2 — 4x) = 2(y+3/2) 2
-(x 2 — 4x + 4) = (y+3/2) 2
-(x — 2) 2 = (y+3/2) 2
(y+3/2) 2 + (x — 2) 2 = 0

Пример №2 . x=1-2/3 sqrt(y 2 -4y-5)
Здесь надо сначала привести к нормальному виду.
3/2(x-1)=sqrt(y 2 -4y-5)
Возводим в квадрат
9/4(x-1) 2 =y 2 -4y-5
9/4x 2 -9/4*2x+9/4-y 2 +4y+5=0
9/4x 2 -9/2x-y 2 +4y+29/4=0

Далее можно решать как с калькулятором, так и без него:
9/4(x-1) 2 =y 2 -4y-5
9/4(x-1) 2 =y 2 -4y+4-4-5
9/4(x-1) 2 =(y 2 -2)-9
9/4(x-1) 2 -(y 2 -2) = -9
-1/4(x-1) 2 +1/9(y 2 -2) = 1

Примеры решений: кривые второго порядка

В этом разделе вы найдете бесплатные примеры решений задач по аналитической геометрии на плоскости на тему Кривые второго порядка: приведение к каноническому виду, нахождение характеристик, построение графика т.п.

Кривые 2-го порядка: решения онлайн

Задача 1. Привести к каноническому виду уравнение кривой 2 порядка, найти все ее параметры, построить кривую.

Задача 2. Дана кривая. Привести к каноническому виду. Построить и определить вид кривой.

Задача 3. Выяснить вид кривой по общему уравнению, найти её параметры и положение в системе координат. Сделать рисунок.

Задача 4. Общее уравнение кривой второго порядка привести к каноническому. Найти координаты центра, координаты вершин и фокусов. Написать уравнения асимптот и директрис. Построить линии на графики, отметить точки.

Задача 5. Дана кривая $y^2+6x+6y+15=0$.
1. Докажите, что данная кривая – парабола.
2. Найдите координаты ее вершины.
3. Найдите значения ее параметра $р$.
4. Запишите уравнение ее оси симметрии.
5. Постройте данную параболу.

Задача 6. Дана кривая $5x^2+5y^2+6xy-16x-16y=16$.
1. Докажите, что эта кривая – эллипс.
2. Найдите координаты центра его симметрии.
3. Найдите его большую и малую полуоси.
4. Запишите уравнение фокальной оси.
5. Постройте данную кривую.

Задача 7. Найти уравнения параболы и её директрисы, если известно, что парабола имеет вершину в начале координат и симметрична относительно оси $Ox$ и что точка пересечения прямых $y=x$ и $x+y-2=0$ лежит на параболе.

Задача 8. Составить уравнение кривой, для каждой точки которой отношение расстояния до точки $F(0;10)$ к расстоянию до прямой $x=-4$ равно $\sqrt<2/5>$. Привести это уравнение к каноническому виду и определить тип кривой.

Задача 9. Даны уравнения асимптот гиперболы $y=\pm 5x/12$ и координаты точки $M(24,5)$, лежащей на гиперболе. Составить уравнение гиперболы.

Задача 10. Даны уравнение параболы $y=1/4 x^2+1$ и точка $C(0;2)$, которая является центром окружности. Радиус окружности $r=5$.
Требуется найти
1) точки пересечения параболы с окружностью
2) составить уравнение касательной и нормали к параболе в точках её пересечения с окружностью
3) найти острые углы, образуемые кривыми в точках пересечения. Чертёж.

3.8. Приведение уравнения к каноническому виду

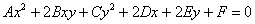
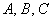
Эта задача следовала за нами практически с самого начала главы и в заключительном параграфе мы окончательно разберёмся, как общее уравнение линии второго порядка ( не равны одновременно нулю) свести к одному из девяти канонических случаев.

В предыдущих параграфах мы очень подробно отработали частный случай уравнения, когда коэффициент :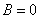
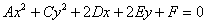
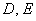
(не равны нулю одновременно)

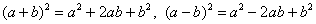
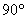
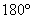
Такое уравнение приводится методом выделения полного квадрата(ов) с дальнейшим применением формул , далее осуществляется поворот (опционально) на угол либо в некоторых случаях на и непременно параллельный перенос линии или системы координат.

…У вас такое уравнение? Значит, вам хватит материалов предыдущих параграфов!

Не такое? Значит, не хватит 🙂

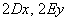
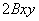
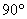
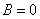
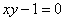
Как многие подметили, члены общего уравнения «отвечают» за параллельный перенос, и логично предположить, что ненулевое слагаемое «отвечает» за поворот (за исключением угла и кратных ему углов, при которых , и мы отделываемся лёгким испугом).Простейший пример поворота на «нехалявный» угол нам уже встречался – это неканонически расположенная «школьная» гипербола .

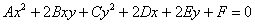
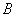
Уравнение с ненулевым коэффициентом неприятно тем, что в общем случае его невозможно привести к каноническому виду с помощью обычных средств алгебры: переноса слагаемых, их группировки, вынесений за скобки, выделения полных квадратов и прочей школьной самодеятельности. Поэтому на помощь приходится привлекать более мощные методы решения.

Рассмотрим в качестве примера уравнение 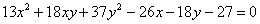. Какие будут идеи? …Да ладно с ними, с идеями, тут даже не понятно, какую линию оно задаёт. Эллипс? Гиперболу? Параболу? Что-то другое из классификации?

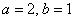
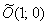
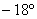
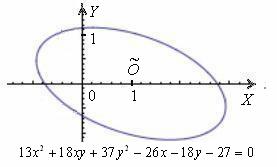
Немного потраченного времени, и вы научитесь довольно легко находить ответы на эти вопросы, в частности, без особых проблем сможете определить, что данное уравнение определяет эллипс с полуосями , который расположен центром в точке и повёрнут относительного своего канонического положения на отрицательный угол, составляющий примерно :
Мысленно возьмите эллипс в руки, поверните его на любой угол и переместите в произвольное место плоскости. Новому положению эллипса будет соответствовать совершенно другое уравнение, и если вам предъявить его без чертежа, то никто в жизнь не догадается, что оно определяет тот же самый эллипс.

Именно поэтому и появилась задача приведения уравнения к каноническому виду – чтобы независимо от расположения линии выяснить, что это за зверь и каким нравом он обладает.
Выше я рассматривал два способа приведения. Применительно к нашему примеру:

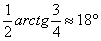
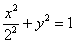
1) Осуществим параллельный перенос эллипса центром в начало координат (представляем мысленно) и повернём его на угол (против часовой стрелки). В результате получится нужное уравнение .

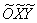
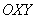
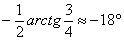
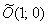
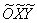
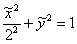
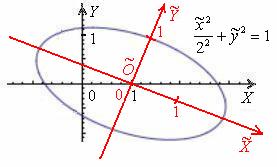
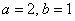
2) Перейдём к прямоугольной системе координат , которая получается путём поворота исходной системы координат на вокруг начала координат и её параллельного переноса центром в точку . Таким образом, в новой системе координат уравнение данного эллипса запишется в каноническом виде :
«Навскидку» второй способ кажется вычурным и неуклюжим, однако, если немного призадуматься, то он более корректен. И толстый намёк на это уже проскочил чуть выше: куда бы мы ни переместили данную линию, какую бы систему координат ни выбрали – эллипс останется тем же самым эллипсом с полуосями , своими фокусами и другими индивидуальными характеристиками.

Но стОит ли перемещать САМУ линию? Представьте, что крыша вашего дома имеет эллиптическую форму, и шаловливый Карлсон выбрал начало координат на трубе кочегарки J. Что вы будете делать, чтобы с комфортом исследовать эллипс? Разумеется, не станете переносить крышу, а перейдёте к удобной системе координат.

То есть, система координат относительна и вторична по отношению к тому или иному объекту. Следовательно, вполне логично и правомерно тревожить именно её, а не «уникальный» эллипс, крышу дома или что-то ещё.

А суть преамбулы состоит в том, что далее мы будем приводить уравнение линии 2-го порядка путём перехода к новой прямоугольной системе координат, в которой уравнение исследуемой линии примет канонический вид.

Существует несколько практических методов приведения уравнения линии к каноническому виду, причём, некоторые из них являются достаточно трудными. Я постараюсь составить максимально простой конспект, доступный человеку с любым уровнем подготовки.

Для этого нам потребуется ещё одно теоретическое понятие:

Все линии 2-го порядка можно разделить на две большие группы:

1) центральные линии, обладающие единственным центром (точкой) симметрии (эллипс, мнимый эллипс, гипербола, пара мнимых или действительных пересекающихся прямых);

2) нецентральные линии, у которых центры симметрии отсутствуют (парабола), либо их бесконечно много (пара действительных или мнимых параллельных прямых, пара совпавших прямых).

Итак, вы счастливый обладатель уравнения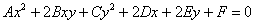
с ненулевым коэффициентом .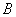

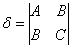
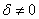
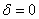
С чего начать? На первом шаге целесообразно выяснить, к какой группе относится линия. Для этого нужно мысленно либо на черновике составить и вычислить определитель . Если , то перед нами уравнение центральной линии, если же – то нецентральной.

Для уравнения :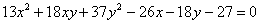
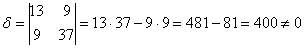
, значит, оно определяет центральную линию.

Зачем это нужно? Чтобы выбрать наиболее выгодный способ решения. Да, конечно, ваш учебный план может и не предоставить возможность выбора, но, тем не менее, я постараюсь провести вас через дебри самой комфортной и короткой тропинкой.

Для приведения уравнения центральной линии, по моему мнению, лучше всего использовать метод инвариантов. Но, к сожалению, он перестаёт работать в нецентральном случае, поэтому на помощь придётся привлечь достаточно трудоёмкий универсальный способ решения либо ортогональное преобразование квадратичной формы (но тут уже надо ориентироваться в другой теме). Сначала разберём одно, затем другое, и даже если вам нужно разделаться лишь с нецентральной линией, постарайтесь не пропускать нижеследующий параграф, поскольку вся информация взаимосвязана: