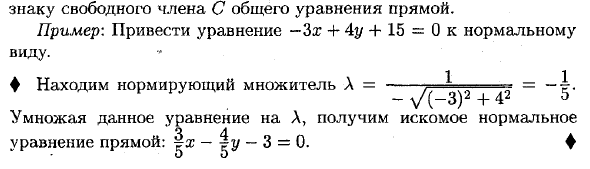Уравнение линии y2 x 1

Различные виды уравнений прямой на плоскости

Различные виды уравнений прямой на плоскости

• Различные типы уравнений, действующих непосредственно на плоскости Самая простая линия — это прямая линия. Различные способы определения прямых соответствуют различным типам уравнений в декартовых системах координат. 1. Линейное уравнение с угловым коэффициентом Дает произвольную прямую линию на плоскости Ohu, которая не параллельна оси Oy. Его положение полностью определяется ординатой b пересечения N (Q; b) с осью Oy и углом a между осью Oh и линией. Под углом o; (0 ^ a Людмила Фирмаль

Знак свободного члена C общего уравнения для прямой. Пример: приведите уравнение -3x-b 4y + 15 = 0 к стандартной форме. ♦ Коэффициент нормализации Л = — ^ Д3 ^ 2 + 42 = Умножьте это уравнение на A, чтобы получить желаемое нормальное уравнение для линии. — 3 = 0.Это удовлетворяется координатами любой точки M (x; y) на прямой.

Вы можете видеть, что любая точка P (x; y) Примеры решения и задачи с методическими указаниями

• Не существует В этом случае линейное уравнение имеет вид х = а, (2) Где а — абсцисса пересечения линии и оси Ox. Обратите внимание, что уравнения (1) и (2) являются линейными уравнениями. 2. Общее уравнение прямой Рассмотрим уравнение первого порядка относительно общего вида x и y. Ax + By + C = 0, (3) Где A, B и C — произвольные числа, а A и B — одновременно ненулевые. Уравнение (3) указывает, что это линейное уравнение. Есть два случая. Если B = 0, форма уравнения (3) имеет вид Ax + C = 0, AΦ0, т.е. x = -Это линейное уравнение, параллельное оси Oy и проходящее через точку В случае ΦΦ0 y =-получается из уравнения (3).

Это линейное уравнение с угловым коэффициентом k = tgc * = -. Некоторые частные случаи общего уравнения прямой: 1) Если A = 0, уравнение сводится к виду y =. Это линейное уравнение, параллельное оси Ox 2) Когда B = 0, линия параллельна оси Oy. 3) Если C = 0, получить Ax + By = 0. Координаты точки 0 (0; 0) удовлетворяют уравнению, и линия проходит через начало координат.

Следовательно, уравнение (3) является линейным уравнением и называется общим линейным уравнением. Людмила Фирмаль

Линейное уравнение через заданную точку В этом направлении Сделайте так, чтобы линия проходила через точку M (x0; y0), и ее направление характеризуется угловым коэффициентом k. Уравнение для этой линии можно записать в виде y = kx 4-6. Поскольку прямая проходит через точку M (x0, y0), координаты точки удовлетворяют уравнению линии y0 = kx o + b.

Следовательно, 6 = уо-кхо. Подставляя значение b в выражение y = kx + b, получаем искомое выражение для строки y = kx + yo-kx0. у-йо = к (х-хо). (4) Уравнение (4) с различными значениями k также называется уравнением пучка вокруг точки M (x0 ‘, Y0). • Из этого карандаша невозможно определить только прямые линии, параллельные оси Oy. 4. Уравнение прямой, проходящей через две точки Пусть прямая проходит через точки M \ (x \ y ) и M2 (x2 ‘, Y2). Форма уравнения для прямой, проходящей через точку Mb: Y

2 / i = k (x-zi), (5) Где k — неизвестный коэффициент Поскольку прямая проходит через точку M2 (^ 22/2)>, координаты этой точки должны удовлетворять уравнению (5): Y2-Y1- = k (x2-x1).

Найти k = ^ отсюда — заменить найденное X2-X \ Получите уравнение для прямой, которая проходит через значения k, точек M \ и M ^ в уравнении (5). L = (б) 2 / 2-2 / 1- Для этого уравнения Xi × X2, Y \ Φy-X2 = xi прямая, проходящая через точки M \ yi) и M2 (x2] Y2), предполагается параллельной оси ординат. Форма уравнения: х = х . Если y2 = 2 / s, уравнение линии можно записать в виде y = y / i. Линия M-yM2 параллельна горизонтальной оси.

Уравнение отрезка Линия пересекает ось Ox в точке M \ (a; 0) и ось Oy в точке Mg (0; b). В этом случае уравнение (6) принимает следующий вид: U- 0 Это 6-0 0-а ‘ Это уравнение называется линейным сегментным уравнением. Это связано с тем, что числа a и b указывают, какой отрезок отрезает линия по координатным осям. , х-а Х у

+ I = L a b в Mg (0; 6) б \ ИЛИ ®

Уравнение прямой через заданную точку, перпендикулярную этому вектору Найти линейное уравнение через заданную точку M0 (x0 \ y0), перпендикулярную данному ненулевому вектору n = (A; B). Возьмем произвольную точку M (x; y) на прямой и рассмотрим вектор M0M- (x-x0; Y-Yo). • Векторы n и McM являются вертикальными, поэтому их скалярное произведение равно нулю. A (x-x0) + B (y-yo) = 0. (7) Уравнение (7) называется уравнением прямой, проходящей через данную точку, перпендикулярную данному вектору и y. Вектор ri = (A) B), перпендикулярный прямой, называется вектором нормали этой прямой.

Уравнение (7) можно переписать в следующем формате Ax + By + C = 0, (8) Где A и B — координаты нормального вектора, а C = —Aho — W / o — свободный член. Уравнение (8) является общим уравнением для линии (см. (3)). 7. Полярные координатные уравнения для прямых Найти линейные уравнения в полярных координатах. Его положение может быть определено путем указания расстояния p от полюса O до конкретной линии и угла a между полюсом OP и осью I через полюс O, перпендикулярный этой линии. Для любой точки M (r;

с другой стороны, pR / OM = \ OM \ cos (a-

Следовательно, линейное уравнение (9) в декартовой системе координат принимает вид: x-cosо4-у • sinа-р = 0. (10) Уравнение (10) называется линейным нормальным уравнением. 44 года п / / a \ x о Вот как можно сделать уравнение (3) прямой в виде (10). Умножим все слагаемые в уравнении (3) на некоторый коэффициент, чтобы получить Л ^ ОХЛх + ХВу + АС = 0. Это уравнение становится уравнением (10). В результате должно быть выполнено уравнение: A / 4 = cos a-, XB = sin a, A C = -p. Из первых двух уравнений найдите Л2А2 + A2J52 = cos2 a + sin2а, т.е. А = ±> * y / A2 + B’2 Х называется нормировочным фактором. Согласно третьему уравнению АС = -р, знак нормировочного коэффициента меняется на противоположный

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Уравнение прямой, виды уравнения прямой на плоскости

В прошлом материале мы рассмотрели основные моменты, касающиеся темы прямой на плоскости. Теперь же перейдем к изучению уравнения прямой: рассмотрим, какое уравнение может называться уравнением прямой, а также то, какой вид имеет уравнение прямой на плоскости.

Определение уравнения прямой на плоскости

Допустим, что есть прямая линия, которая задана в прямоугольной декартовой системе координат O х у .

Прямая линия – это геометрическая фигура, которая состоит из точек. Каждая точка имеет свои координаты по осям абсцисс и ординат. Уравнение, которое описывает зависимость координат каждой точки прямой в декартовой системе O x y , называется уравнением прямой на плоскости.

Фактически, уравнение прямой на плоскости – это уравнение с двумя переменными, которые обозначаются как x и y . Уравнение обращается в тождество при подстановке в него значений любой из точек прямой линии.

Давайте посмотрим, какой вид будет иметь уравнение прямой на плоскости. Этому будет посвящен весь следующий раздел нашей статьи. Отметим, что существует несколько вариантов записи уравнения прямой. Объясняется это наличием нескольких способов задания прямой линии на плоскости, и также различной спецификой задач.

Общее уравнение прямой линии

Познакомимся с теоремой, которая задает вид уравнения прямой линии на плоскости в декартовой системе координат O x y .

Уравнение вида A x + B y + C = 0 , где x и y – переменные, а А , В и C – это некоторые действительные числа, из которых A и B не равны нулю, задает прямую линию в декартовой системе координат O x y . В свою очередь, любая прямая линия на плоскости может быть задана уравнением вида A x + B y + C = 0 .

Таким образом, общее уравнение прямой на плоскости имеет вид A x + B y + C = 0 .

Поясним некоторые важные аспекты темы.

Посмотрите на рисунок.

Линия на чертеже определяется уравнением вида 2 x + 3 y — 2 = 0 , так как координаты любой точки, составляющей эту прямую, удовлетворяют приведенному уравнению. В то же время, определенное количество точек плоскости, определяемых уравнением 2 x + 3 y — 2 = 0 , дают нам прямую линию, которую мы видим на рисунке.

Общее уравнение прямой может быть полным и неполным. В полном уравнении все числа А , В и C отличны от нуля. Во всех остальных случаях уравнение считается неполным. Уравнение вида A x + B y = 0 определяет прямую линию, которая проходит через начало координат. Если A равно нулю, то уравнение A x + B y + C = 0 задает прямую, расположенную параллельно оси абсцисс O x . Если B равно нулю, то линия параллельна оси ординат O y .

Вывод: при некотором наборе значений чисел А , В и C с помощью общего уравнения прямой можно записать любую прямую линию на плоскости в прямоугольной системе координат O х у .

Прямая, заданная уравнением вида A x + B y + C = 0 , имеет нормальный вектор прямой с координатами A , B .

Все приведенные уравнения прямых, которые мы рассмотрим ниже, могут быть получены из общего уравнения прямой. Также возможен и обратный процесс, когда любое из рассматриваемых уравнений может быть приведено к общему уравнению прямой.

Разобраться во всех нюансах темы можно в статье «Общее уравнение прямой». В материале мы приводим доказательство теоремы с графическими иллюстрациями и подробным разбором примеров. Особое внимание в статье уделяется переходам от общего уравнения прямой к уравнениям других видов и обратно.

Уравнение прямой в отрезках

Уравнение прямой в отрезках имеет вид x a + y b = 1 , где a и b – это некоторые действительные числа, которые не равны нулю. Абсолютные величины чисел a и b равны длине отрезков, которые отсекаются прямой линией на осях координат. Длина отрезков отсчитывается от начала координат.

Благодаря уравнению можно легко построить прямую линию на чертеже. Для этого необходимо отметить в прямоугольной системе координат точки a , 0 и 0 , b , а затем соединить их прямой линией.

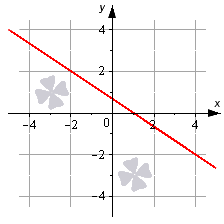
Построим прямую, которая задана формулой x 3 + y — 5 2 = 1 . Отмечаем на графике две точки 3 , 0 , 0 , — 5 2 , соединяем их между собой.

Дополнительно рекомендуем ознакомиться с материалом, изложенным в статье «Уравнение прямой в отрезках».

Уравнение прямой с угловым коэффициентом

Эти уравнения, имеющие вид y = k · x + b должны быть нам хорошо известны из курса алгебры. Здесь x и y – это переменные, k и b – это некоторые действительные числа, из которых k представляет собой угловой коэффициент. В этих уравнениях переменная у является функцией аргумента x .

Дадим определение углового коэффициента через определение угла наклона прямой к положительному направлению оси O x .

Для обозначения угла наклона прямой к положительному направлению оси O x в декартовой системе координат введем величину угла α . Угол отсчитывается от положительного направления оси абсцисс до прямой линии против хода часовой стрелки. Угол α считается равным нулю в том случае, если линия параллельна оси O x или совпадает с ней.

Угловой коэффициент прямой – это тангенс угла наклона этой прямой. Записывается это следующим образом k = t g α . Для прямой, которая располагается параллельно оси O y или совпадает с ней, записать уравнение прямой с угловым коэффициентом не представляется возможным, так как угловой коэффициент в этом случае превращается в бесконечность (не существует).

Прямая, которая задана уравнением y = k · x + b , проходит через точку 0 , b на оси ординат. Это значит, что уравнение прямой с угловым коэффициентом y = k · x + b , задает на плоскости прямую линию, которая проходит через точку 0 , b и образует угол α с положительным направлением оси O x , причем k = t g α .

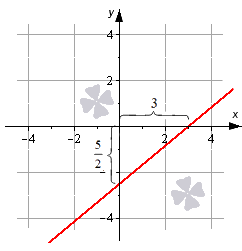
Изобразим прямую линию, которая определяется уравнением вида y = 3 · x — 1 .

Эта линия должна пройти через точку ( 0 , — 1 ) . Угол наклона α = a r c t g 3 = π 3 равен 60 градусов к положительному направлению оси O x . Угловой коэффициент равен 3

Обращаем ваше внимание, что с помощью уравнения прямой с угловым коэффициентом очень удобно искать уравнение касательной к графику функции в точке.

Больше материала по теме можно найти в статье «Уравнение прямой с угловым коэффициентом». Помимо теории там размещено большое количество графических примеров и подробный разбор задач.

Каноническое уравнение прямой на плоскости

Данный вид уравнения имеет вид x — x 1 a x = y — y 1 a y , где x 1 , y 1 , a x , a y — это некоторые действительные числа, из которых a x и a y не равны нулю.

Прямая линия, заданная каноническим уравнением прямой, проходит через точку M 1 ( x 1 , y 1 ) . Числа a x и a y в знаменателях дробей представляют собой координаты направляющего вектора прямой линии. Это значит, что каноническое уравнение прямой линии x — x 1 a x = y — y 1 a y в декартовой системе координат O x y соответствует линии, проходящей через точку M 1 ( x 1 , y 1 ) и имеющей направляющий вектор a → = ( a x , a y ) .

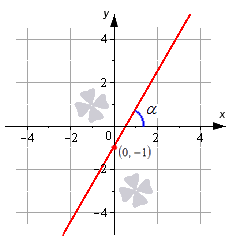
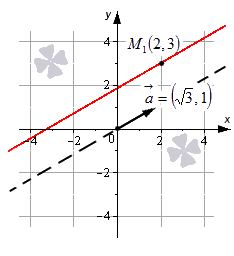
Изобразим в системе координат O x y прямую линию, которая задается уравнением x — 2 3 = y — 3 1 . Точка M 1 ( 2 , 3 ) принадлежит прямой, вектор a → ( 3 , 1 ) является направляющим вектором этой прямой линии.

Каноническое уравнение прямой линии вида x — x 1 a x = y — y 1 a y может быть использовано в случаях, когда a x или a y равно нулю. Наличие ноля в знаменателе делает запись x — x 1 a x = y — y 1 a y условной. Уравнение можно записать следующим образом a y ( x — x 1 ) = a x ( y — y 1 ) .

В том случае, когда a x = 0 , каноническое уравнение прямой принимает вид x — x 1 0 = y — y 1 a y и задает прямую линию, которая расположена параллельно оси ординат или совпадает с этой осью.

Каноническое уравнение прямой при условии, что a y = 0 , принимает вид x — x 1 a x = y — y 1 0 . Такое уравнение задает прямую линию, расположенную параллельно оси абсцисс или совпадающую с ней.

Больше материала на тему канонического уравнения прямой смотрите здесь. В статье мы приводим целый ряд решений задач, а также многочисленные примеры, которые позволяют лучше овладеть темой.

Параметрические уравнения прямой на плоскости

Данные уравнения имеют вид x = x 1 + a x · λ y = y 1 + a y · λ , где x 1 , y 1 , a x , a y — это некоторые действительные числа, из которых a x и a y не могут быть одновременно равны нулю. В формулу вводится дополнительный параметр λ , который может принимать любые действительные значения.

Назначение параметрического уравнения в том, чтобы установить неявную зависимости между координатами точек прямой линии. Для этого и вводится параметр λ .

Числа x , y представляют собой координаты некоторой точки прямой. Они вычисляются по параметрическим уравнениям прямой при некотором действительном значении параметра λ .

Предположим, что λ = 0 .

Тогда x = x 1 + a x · 0 y = y 1 + a y · 0 ⇔ x = x 1 y = y 1 , т. е. точка с координатами ( x 1 , y 1 ) принадлежит прямой.

Обращаем ваше внимание на то, что коэффициенты a x и a y при параметре λ в данном виде уравнений представляют собой координаты направляющего вектора прямой линии.

Рассмотрим параметрические уравнения прямой линии вида x = 2 + 3 · λ y = 3 + λ . Прямая, заданная уравнениями, в декартовой системе координат проходит через точку ( x 1 , y 1 ) и имеет направляющий вектор a → = ( 3 , 1 ) .

Больше информации ищите в статье «Параметрические уравнения прямой на плоскости».

Нормальное уравнение прямой

Нормальное уравнение прямой имеет вид , A x + B y + C = 0 , где числа А , В , и C таковы, что длина вектора n → = ( A , B ) равна единице, а C ≤ 0 .

Нормальным вектором линии, заданной нормальным уравнением прямой в прямоугольной системе координат O х у , является вектор n → = ( A , B ) . Эта прямая проходит на расстоянии C от начала координат в направлении вектора n → = ( A , B ) .

Еще одним вариантом записи нормального уравнения прямой линии является cos α · x + cos β · y — p = 0 , где cos α и cos β — это два действительных числа, которые представляют собой направляющие косинусы нормального вектора прямой единичной длины. Это значит, что n → = ( cos α , cos β ) , справедливо равенство n → = cos 2 α + cos 2 β = 1 , величина p ≥ 0 и равна расстоянию от начала координат до прямой.

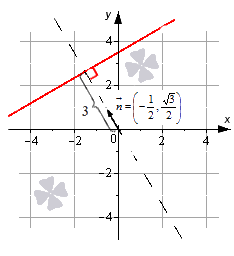
Рассмотрим общее уравнение прямой — 1 2 · x + 3 2 · y — 3 = 0 . Это общее уравнение прямой является нормальным уравнением прямой, так как n → = A 2 + B 2 = — 1 2 2 + 3 2 = 1 и C = — 3 ≤ 0 .

Уравнение задает в декартовой системе координат 0ху прямую линию, нормальный вектор которой имеет координаты — 1 2 , 3 2 . Линия удалена от начала координат на 3 единицы в направлении нормального вектора n → = — 1 2 , 3 2 .

Обращаем ваше внимание на то, что нормальное уравнение прямой на плоскости позволяет находить расстояние от точки до прямой на плоскости.

Если в общем уравнении прямой A x + B y + C = 0 числа А , В и С таковы, что уравнение A x + B y + C = 0 не является нормальным уравнением прямой, то его можно привести к нормальному виду. Подробнее об этом читайте в статье «Нормальное уравнение прямой».

Уравнение прямой, проходящей через две точки онлайн

С помощю этого онлайн калькулятора можно построить уравнение прямой, проходящей через две точки. Дается подробное решение с пояснениями. Для построения уравнения прямой задайте размерность (2-если рассматривается прямая на плоскости, 3- если рассматривается прямая в пространстве), введите координаты точек в ячейки и нажимайте на кнопку «Решить».

Предупреждение

Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.

Уравнение прямой, проходящей через две точки − примеры и решения

Пример 1. Построить прямую, проходящую через точки A(2, 1, 1), B(3, 1, -2).

(1)

Подставив координаты точек A и B в уравнение (1), получим:

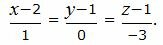(Здесь 0 в знаменателе не означает деление на 0).

Составим параметрическое уравнение прямой:

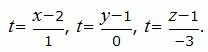Выразим переменные x, y, z через параметр t :

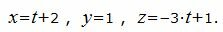Каноническое уравнение прямой, проходящей через точки A(2, 1, 1), B(3, 1, -2) имеет следующий вид:

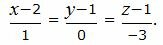Параметрическое уравнение прямой, проходящей через точки A(2, 1, 1), B(3, 1, -2) имеет следующий вид:

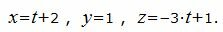Пример 2. Построить прямую, проходящую через точки A(1, 1/5, 1) и B(−2, 1/2, −2).

(2)

Подставив координаты точек A и B в уравнение (2), получим:

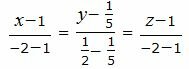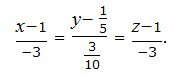Составим параметрическое уравнение прямой:

Выразим переменные x, y, z через параметр t :

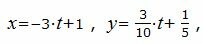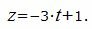Каноническое уравнение прямой, проходящей через точки A(1, 1/5, 1) и B(−2, 1/2, −2) имеет следующий вид:

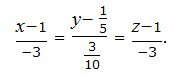Параметрическое уравнение прямой, проходящей через точки A(1, 1/5, 1) и B(−2, 1/2, −2) имеет следующий вид: