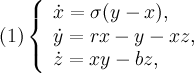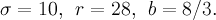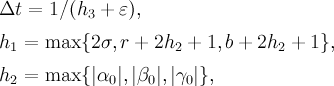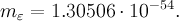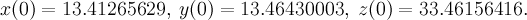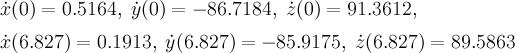Уравнение лоренца методы ускорения высоковольтный индукционный резонансный

Динамическая система Лоренца и вычислительный эксперимент

Данный пост является продолжением моей статьи [1] на Хабрахабре об аттракторе Лоренца. Здесь рассмотрим метод построения приближенных решений соответствующей системы, уделив внимание программной реализации.

Динамической системой Лоренца является автономная система обыкновенных дифференциальных уравнений третьего порядка

где 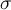, r и b являются положительными числами. Для исследования поведения решений системы обычно берут классические значения параметров системы, т.е.

Как было отмечено в статье [1], в этом случае в системе (1) имеет место неустойчивость ее решений на аттракторе. По сути, это делает некорректным применение классических численных методов на больших отрезках времени (а на таких отрезках и строятся предельные множества динамических систем). 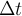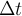Одним из вариантов преодоления этой проблемы является переход к высокоточным вычислениям, но такой подход ставит исследователя в жесткие рамки: во-первых, малая степень свободы для уменьшения ошибки (изменение величины шага интегрирования и точности представления вещественного числа для управления вычислительным процессом), во-вторых, большой объем вычислений при очень малых .

Другим вариантом решения данной проблемы может быть применение метода степенных рядов. В работе [2] описана модификация этого метода для динамических систем вида (1), позволяющая достаточно быстро определять коэффициенты разложений

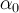
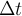
где коэффициенты , и определяются начальными условиями; также получена длина (шаг) отрезка сходимости рядов (2):

если , то , иначе ,

— любое положительное число.

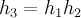
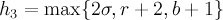
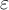
Заметим, что приведенная в статье [2] схема получения длины отрезка сходимости степенных рядов может по аналогии перенесена на другие динамические системы третьего порядка с нелинейностями вида (1) (например, система, описывающая поведение саморазвивающейся рыночной экономики [3, с. 261]).

Несмотря на то, что все траектории системы (1) ограничены и ее правая часть всюду аналитична, первоначальный вычислительный эксперимент показал, что радиус сходимости рядов (2) ограничен и зависит от выбора начальных условий. Поэтому описанным способом мы можем получить только часть траектории. Процедура построения дуги траектории на любом отрезке времени заключается в сшивке частей траектории, составляющих искомое решение, на которых сходятся ряды (2). 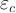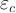Ошибкой интегрирования, накапливаемой при переходе от дуги к дуге траектории из-за погрешности нахождения текущего приближенного решения, можно управлять за счет варьирования точности разложения в степенной ряд. Использование при этом высокоточных вычислений позволяет продолжить решения на очень большие промежутки времени, поскольку невозможно сделать сколь угодно малой из-за ограничения на машинный эпсилон.

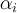
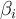
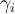
По формулам (3) вычисляем , и до такого значения i, при котором имеет место оценка

Понятно, что значительного накопления ошибки интегрирования на длинных временных отрезках нам и здесь не избежать, поэтому будем реализовывать высокоточные вычисления с плавающей точкой на базе библиотеки GNU MPFR Library, а точнее, C++-интерфейса библиотеки MPFR для работы с вещественными числами произвольной точности — MPFR C++. Она удобна тем, что в ней имеется класс mpreal с перегруженными арифметическими операциями и дружественными математическими функциями. Для установки библиотеки в Ubuntu Linux выполним

Кроме пакета libmpfr-dev менеджеров пакетов потянет еще и libgmp-dev. Это devel-пакет библиотеки GNU Multiple Precision Arithmetic Library или GMP (MPFR является ее расширением).

Рассмотрим пример кода на C++ вычисления значений фазовых координат в конечный момент времени, а также проверки найденных значений.

Для компиляции файла lorenz.cpp с этим кодом выполним следующее

Как видно из листинга программы, для хранения значений коэффициентов степенных рядов используются векторы из библиотеки STL. Было принято, что количество бит под мантиссу вещественного числа равно 180. Диапазон изменения экспоненты — по умолчанию от до (на 32-битных платформах). Функция machine_epsilon() определения машинного эпсилон была использована для того, чтобы узнать его значение для заданного представления вещественного числа. В данном случае

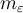
Приведем результаты вычислительного эксперимента. В качестве начальных условий возьмем значения, близкие к аттрактору Лоренца:

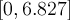
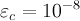
Отрезок времени, на котором производилось вычисления, — . Первоначально точность оценки общего члена ряда бралась равной . Этого достаточно, чтобы получить результат

;

(уменьшая значение , значения координат не изменятся). При этом можно брать вещественные числа с меньшим объемом памяти.

Значения производных, как и значения координат, приведены для того, чтобы проиллюстрировать факт возвращения траектории в окрестность начальной точки, но незамыкания, как это следовало бы ожидать из гипотезы существования циклов в системе (1). После такого сближения точка траектории уходит от своего начального положения, но потом опять возвращается в ее окрестность. Такое поведение предсказывает качественная теория дифференциальных уравнений (устойчивость по Пуассону точек рекуррентных траекторий на аттракторе; это было указано в [1] и обсуждено на конференции [4]).

Указанная разрядность для вещественного числа была выбрана с целью отследить не только возврат траектории системы Лоренца в окрестность начальных условий [1, рис. 1], но и для прохода назад по времени от конечной точки к начальной по дуге траектории (равенство параметра way функции calc() -1). Тогда в расчетах нужно брать 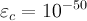. В результате получаются значения, совпадающие с начальными до седьмого знака после запятой (метод toString() класса mpreal, вызванный без параметров, говорит о преобразовании числа в строку с максимальным количеством знаков после запятой):

x = 13.412656286837273085165416945301946328440634370684244
y = 13.4643000297481126631507883918720904312092673686014399
z = 33.4615641630148784946354299167181879731357599130041067

Такое малое значение выбрано потому, что при движении по траектории в отрицательные значения времени наблюдается сильная неустойчивость решений — они сразу уходят в бесконечность от аттрактора, поскольку мы при расчетах находимся вблизи от него, а не непосредственно на нем.

В программе также предусмотрено фиксированное значение шага. Проверено, число 0.02 может быть использовано для построений приближенных решений вблизи аттрактора Лоренца. Это значение гораздо больше того, которое получается из приведенной оценки из работы [2] (флаг FL_CALC равен 1) для любых начальных условий, но при удалении начальной точки на значительное расстояние от аттрактора метод перестает работать (ряды не сходятся).

В работе [5, с. 90, 91] для исследования траекторий системы (1) применяется метод Эйлера с переменным шагом интегрирования. Величина выбирается с отслеживанием ошибки на текущем шаге (т.е. локальный контроль), используя интервальную арифметику. Однако нет проверки общей ошибки интегрирования. Проход назад по времени, описанный выше, нам гарантирует правильность построения приближенного решения. Варьируя точностью оценки общего члена ряда, можно уменьшить ошибку на шаге, что не позволяет метод Эйлера. Также в рассмотренной модификации метода степенных рядов преимуществом перед общей схемой метода рядов Тейлора является быстрый расчет по формулам (3) коэффициентов разложения по сравнению с процедурой символьного дифференцирования правых частей уравнений системы (кроме того, в нелинейном случае под символьные выражения требуется много памяти для их хранения при вычислении производных высших порядков).

Таким образом, зная состояние системы Лоренца в прошлом, мы с достаточной степенью точности можем предсказать поведение ее траекторий в течение длительных интервалов времени, а также вернуться назад. По сути здесь нарушается формальное определение хаоса [6, с. 118, 119].

ЛО́РЕНЦА — МА́КСВЕЛЛА УРАВНЕ́НИЯ

ЛО́РЕНЦА – М А́КСВЕЛЛА УРАВНЕ́НИЯ, осн. урав­не­ния мик­ро­ско­пич. клас­сич. элек­тро­ди­на­ми­ки, оп­ре­де­ляю­щие элек­тро­маг­нит­ные по­ля, соз­да­вае­мые отд. за­ря­жен­ны­ми час­ти­ца­ми, дви­жу­щи­ми­ся (или по­коя­щи­ми­ся) в ва­куу­ме. Л. – М. у. ле­жат в ос­но­ве элек­трон­ной тео­рии, раз­ра­бо­тан­ной Х. А. Ло­рен­цем в кон. 19 – нач. 20 вв. Л. – М. у. яв­ля­ют­ся след­ст­ви­ем пе­ре­но­са фе­но­ме­но­ло­ги­че­ских Мак­свел­ла урав­не­ний, оп­ре­де­ляю­щих на­блю­дае­мое мак­ро­ско­пи­че­ское (ус­ред­нён­ное) элек­тро­маг­нит­ное по­ле, на мик­ро­ско­пи­че­ское (не­по­сред­ст­вен­но не­на­блю­дае­мое) элек­тро­маг­нит­ное по­ле и име­ют вид: $$\textrm \,\boldsymbol = -\frac<\partial \boldsymbol b><\partial t>, \quad \textrm\,\boldsymbol=μ_0 \left( \sum_iρ_iv_i +ε_0\frac<\partial \boldsymbol><\partial t>\right),\\ \textrm