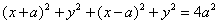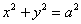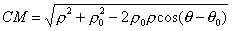Уравнение луча проходящего через полюс под углом

4.4. Уравнение линии в полярных координатах

По существу, уравнение линии в полярной системе координат представляет собой функцию полярного радиуса от полярного угла (аргумента). При этом полярный угол учитывается в радианах (!) и непрерывно принимает значения от до (иногда следует рассмотреть до бесконечности, или же в ряде задач для удобства от до ). Каждому значению угла «фи», которое входит в область определения функции , соответствует единственное значение полярного радиуса.

Полярную функцию можно сравнить со своеобразным радаром – когда луч света, исходящий из полюса, вращается против часовой стрелки и «прорисовывает» линию.

«Дежурным» примером полярной кривой является Архимедова спираль . На следующем рисунке изображен её первый виток – когда полярный радиус вслед за полярным углом принимает значения от 0 до :
Далее, пересекая полярную ось в точке , спираль продолжит раскручиваться, бесконечно далеко удаляясь от полюса. Но подобные случаи на практике встречаются довольно редко; более типичная ситуация, когда на всех последующих оборотах мы «пройдёмся по той же самой линии», которая получена в диапазоне .
В первом же примере мы сталкиваемся и с понятием области определения полярной функции: поскольку полярный радиус неотрицателен , то отрицательные углы у функции рассматривать нельзя.

! Примечание: в ряде случаев принято использовать обобщённые полярные координаты, где радиус может быть отрицательным, и такой подход мы вкратце изучим чуть позже

Кроме спирали Архимеда, есть множество других известных кривых, но искусством, как говорится, сыт не будешь, поэтому я подобрал примеры, которые очень часто встречаются в реальных практических заданиях.

Сначала простейшие уравнения и простейшие линии:

Уравнение вида задаёт луч, исходящий из полюса. Действительно, вдумайтесь, если значение угла всегда (каким бы ни было «эр») постоянно, то какая это линия?

Примечание: в обобщённой полярной системе координат данное уравнение задаёт прямую, проходящую через полюс.

Уравнение вида определяет… догадайтесь с первого раза – если для любого угла «фи» радиус остаётся постоянным? Фактически это определение окружности с центром в полюсе радиуса .

Например, . Для наглядности найдём уравнение этой линии в прямоугольной системе координат. Используя полученную ранее формулу , проведём замену:

Возведём обе части в квадрат:
– уравнение окружности с центром в начале координат радиуса 2, что и требовалось проверить.

А теперь оценИте удобство – с окружностью значительно выгоднее работать именно в полярных координатах по причине предельной простоты уравнения .

Рассмотрим более содержательные задачи на построение:

Задача 116

Построить линию

Решение: в первую очередь найдём область определения. Так как полярный радиус неотрицателен, то должно выполняться неравенство . Можно вспомнить школьные правила решения тригонометрических неравенств, но в простых случаях как этот,
я советую более быстрый графический метод решения:

– Посмотрим на график функции (см. Приложение Тригонометрия). Что означает неравенство ? Оно означает, что нас устраивает тот кусок графика, который не ниже оси абсцисс , а именно, его часть на отрезке . И, соответственно, интервал не подходит. Таким образом, область определения нашей функции: , то есть график расположен справа от полюса (по терминологии декартовой системы – в правой полуплоскости).

В полярных координатах часто бывает смутное представление о том, какую линию определяет то или уравнение, поэтому чтобы её построить, необходимо найти принадлежащие ей точки – и чем больше, тем лучше. Обычно ограничиваются десятком-другим (а то и меньшим количеством). Проще всего, конечно же, взять табличные значения угла.

Для бОльшей ясности к отрицательным значениям угла я буду «прикручивать» один оборот (левая колонка), и в силу чётности косинуса соответствующие положительные значения можно заново не считать (справа):

Изобразим полярную систему координат и отложим найденные точки, при этом одинаковые значения «эр» удобно откладывать за один раз, делая парные засечки циркулем по рассмотренной ранее технологии:

В принципе, линия отчётливо прорисовывается, но чтобы стопроцентно подтвердить догадку, давайте найдём её уравнение в декартовой системе координат. Можно применить недавно выведенные формулы , но я расскажу вам о более хитром приёме.

Обе части уравнения искусственно домножаем на «эр»: и используем более компактные формулы перехода:

Выделяя полный квадрат, приводим уравнение к понятному виду:

– уравнение окружности с центром в точке , радиуса 2.

Коль скоро по условию требовалось просто выполнить построение и всё, плавно соединяем найденные точки линией. Ничего страшного, если получится немного неровно, вы же не обязаны были знать, что это окружность 😉

Почему мы не рассмотрели значения угла вне промежутка ?

Ответ прост: нет смысла. Ввиду периодичности функции нас ждёт бесконечный «бег» по построенной окружности.

Несложно провести нехитрый анализ и прийти к выводу, что уравнение вида задаёт окружность диаметра с центром в точке .

Образно говоря, все такие окружности «сидят» на полярной оси и обязательно проходят через полюс. Если же , то весёлая компания перекочует налево – на продолжение полярной оси (подумайте, почему).

Похожая задача для самостоятельного решения:

Задача 117

Построить линию и найти её уравнение в декартовой системе координат.

Систематизируем порядок решения задачи:

Находим область определения функции, для этого удобно посмотреть на синусоиду (Приложение Тригонометрия), чтобы сразу же понять, где синус неотрицателен.

На втором шаге рассчитываем полярные координаты точек, используя табличные значения углов; проанализируйте, нельзя ли сократить количество вычислений?

На третьем шаге откладываем точки в полярной системе координат и аккуратно соединяем их линией.

И, наконец, находим уравнение линии в декартовой системе координат.

Примерный образец решения в конце книги.

Общий алгоритм и технику построения в полярных координатах мы детализируем и существенно ускорим совсем скоро, но перед этим познакомимся ещё с одной распространённой линией:

Уравнение луча проходящего через полюс под углом

Глава 10. Вывод уравнений заранее данных линий

В задачах предыдущего параграфа линия определялась при помощи данного уравнения. Здесь мы будем иметь задачи противоположного характера; в каждой из них линия определяется чисто геометрически, а уравнение ее требуется найти.

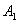
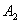
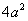
ПРИМЕР 1. В декартовой прямоугольной системе координат вывести уравнение геометрического места точек, сумма квадратов расстояний которых до двух данных точек (-а; 0) и (а; 0) есть величина постоянная, равная .

РЕШЕНИЕ. Обозначим буквой М произвольную точку линии, буквами х и у обозначим координаты этой точки. Так как точка М может занимать на линии любое положение то х и у являются переменными величинами; их называют текущими координатами.

Запишем геометрическое свойство линии символически:

(1).

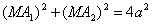
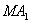
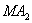
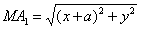
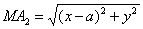
В этом отношении при движении точки М могут меняться длины и . Выразим их через текущие координаты точки М:

, (2)

Подставив полученные выражения в равенство (1), найдем уравнение, связывающее координаты х, у точки М:

Это и есть уравнение данной линии.

Действительно, для каждой точки М, лежающей на этой инии, выполняется условие (1) и, следовательно, координаты точки М будут удовлетворять уравнению (2); для каждой точки М, не лежащей на линии, не будет выполняться условие (1) и, следовательно, ее координаты не будут удовлетворять уравнению (2).

Таким образом, задача решена. Однако уравнение (2) можно упростить; раскрывая скобки и приводя подобные члены, получим уравнение данной линии в виде:

Теперь легко понять, что данная линия есть окружность с центром в начале координат и радиусом, равным а.

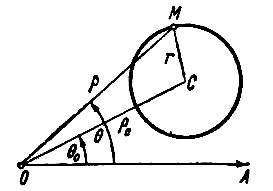
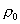
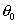
ПРИМЕР 2. В полярной системе координат вывести уравнение окружности, которая имеет центр С( ; ) и радиус r (см. рис.).

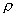
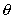
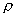
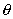
РЕШЕНИЕ. Олозначим буквой М произвольную точку окружности, буквами и — ее полярные координаты. Так как точка М может занимать на окружности любое положение, то и являются переменными величинами. Как и в случае декартовой системы, их называют текущими координатами.

Все точки окружности отстоят от центра на расстоянии r ; запишем это условие символически:

(1).

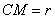
Выразим СМ через текущие координаты точки М (воспользуемся теоремой косинусов):

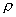
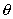
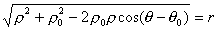
Подставив полученное выражение в равенство (1), найдем уравнение, связывающее координаты , точки М:

(2)

Это и есть уравнение данной окружности.

Действительно, для каждой точки М, лежащей на данной окружности, выполняется условие (1) и , следовательно, координаты точки М будут удовлетворять уравнению (2); для каждой точки М, не лежащей на данной окружности, не будет выполняться условие (1) и, следовательно, ее координаты не будут удовлетворять уравнению (2).

Таким образом, задача решена. Можно лишь несколько упростить полученное уравнение и представить его в виде, свободным от радикала:

.

Геометрическая оптика. Общие свойства лучей

Геометрическая оптика. общие свойства лучей

В рамках электромагнитной теории света его распространение представляет собой волновой процесс. С помощью волновой теории мы можем решать задачи о распространении света, как в однородной среде, так и через любую оптическую систему, т. е. совокупность различных сред, ограниченных теми или иными поверхностями или диафрагмами. Однако в очень многих областях, имеющих важное практическое значение, в частности, при решении вопросов формирования световых пучков (светотехника), образования изображения (оптотехника), решение можно получить гораздо более простым путем, с помощью представлений геометрической оптики. Интуитивно ясный и применяемый обычно без дополнительных объяснений метод геометрической оптики оперирует понятием отдельных световых лучей, поведение которых в окружающих средах было установлено экспериментально, как уже известно из исторического введения. Построения с помощью световых лучей достаточно формальны, удобны в использованиии и в большом числе случаев вполне адекватно описывают формирование даже самых сложных оптических изображений.

Понятие светового луча можно получить из рассмотрения реального светового пучка в однородной среде, из которого при помощи одной или нескольких диафрагм с отверстиями выделяется узкий параллельный пучок. Чем меньше диаметр этих отверстий, тем уже выделяемый пучок, и в пределе, переходя к отверстиям сколь угодно малым, можно, казалось бы, получить световой луч как прямую линию. Однако подобный процесс выделения сколь угодно узкого пучка (луча) невозможен вследствие явления дифракции. Неизбежное угловое расширение реального светового пучка с длиной волны l, пропущенного через диафрагму диаметра D, определяется углом дифракции j » l ¤ D (см. Оптика ч. 2, раздел “Дифракция на круглой апертуре”). Таким образом, световой луч есть абстрактное математическое понятие, а не физический образ, и приближение геометрической оптики на самом деле требует некоторого обоснования и определения границ его применимости.

Только в предельном случае, когда l ® 0, подобное расширение не имело бы места, и можно было бы говорить о луче как о геометрической линии, направление которой определяет направление распространения световой энергии. Таким образом, световой луч есть абстрактное математическое понятие, а не физический образ, и геометрическая оптика есть лишь предельный случай волновой оптики, соответствующий исчезающе малой длине световой волны.

Соотношение j » l ¤ D показывает, что угловое отклонение, нарушающее прямолинейность распространения света в однородной среде, может быть весьма мало, если размеры отверстия или экрана велики по сравнению с длиной волны l. Поэтому в реальной оптике, где l — конечная величина, отступления от законов геометрической оптики должны быть тем меньше, чем больше размеры диафрагмы.

Таким образом, при пользовании законами геометрической (лучевой) оптики нельзя забывать, что они — лишь первое приближение к действительности и что без дифракционных явлений не обходится ни один случай распространения света. Необходимо, следовательно, понимать волновой (дифракционный) смысл этих геометрических построений. Из этого ясно, что законы геометрической оптики имеют ограниченное применение, и надо уметь ориентироваться, при каких условиях применение этих законов допустимо и будет находиться в достаточном соответствии с экспериментом. Оказывается, что даже в практической оптике наиболее тонкие вопросы (например, вопрос о разрешающей силе оптических инструментов) решаются только в рамках теории дифракции.

1.2 Уравнение эйконала

Рассмотрим монохроматическую световую волну с длиной волны в вакууме l0, распространяющуюся в немагнитной (m = 1) среде с показателем преломления . Поле этой волны должно удовлетворять уравнению Гельмгольца

, (1.1)

где – волновой вектор, обратный длине волны.

Будем искать решение этого уравнения в виде

, (1.2)

где L(r) – вещественная скалярная функция координат, имеющая размерность длины и называемая оптическим путем или эйконалом (от греческого eikon – путь). Нетрудно видеть, что равенство L = const определяет поверхность постоянной фазы, т. е. геометрический волновой фронт.

Подставим выражение (1.2) в (1.1) и перейдем к пределу геометрической оптики l®0 (k0®¥), оставив только слагаемые с k02.Тогда получаем:

, или . (1.3)

Уравнение (1.3) называется уравнением эйконала и является основным уравнением, описывающим поведение света в приближении геометрической оптики. Отметим, что при его выводе мы пренебрегли многочисленными слагаемыми, получающимися при дифференцировании уравнения волны (1.2). Отсюда следует, что приближение геометрической оптики справедливо, если изменения амплитуды e на расстоянии порядка длины волны малы по сравнению с самой амплитудой. Это условие, очевидно, нарушается на границе геометрической тени, так как. там интенсивность света, а значит и напряженность поля, меняется скачком. Действительно, именно на границе тени особенно ярко проявляют себя дифракционные эффекты, обусловленные волновой природой света. Нельзя также ожидать, что геометрическая оптика даст правильное описание полей вблизи точек, где имеется резкий максимум интенсивности, например, в окрестности формируемого линзой оптического изображения точечного источника, образующегося в линзе.

Уравнение эйконала можно также записать в векторной форме. Введем единичный вектор s, совпадающий по направлению с вектором grad L, тогда

. (1.4)

Из векторного анализа известно, что вектор градиента всегда ортогонален поверхности уровня функции, т. е. поверхности, на которой функция постоянна. В данном случае поверхность уровня для эйконала представляет собой волновой фронт, следовательно s – орт нормали к волновому фронту. Исходя их уравнений Максвелла можно показать, что направление вектора Пойнтинга, определяющего перенос энергии света, совпадает с вектором s. Таким образом, линии векто­ра s представляют собой геометрические световые лучи. Рис. 1.1 иллюстрирует тот факт, что семейство волновых фронтов (a, b, c) и семейство световых лучей (1, 2, 3) образуют ортогональную (в общем случае криволинейную) сеть.

1.3 Законы распространения лучей

Оптический путь

Рассмотрим два последовательных близких положения волнового фронта (рис. 1.2). Из (1.4) следует, что в силу ортогональности отрезка ds волновым поверхностям , т. е.

. (1.5)

Это означает, что расстояние между соседними волновыми фронтами увеличивается по мере уменьшения показателя преломления. Таким образом, на рис. 1.1 показатель преломления среды в левой части рисунка больше, чем в правой. Из сказанного следует, что оптическая длина пути совпадает с геометрической только в вакууме (n = 1), во всех других средах dL > ds.

Учтем, что , где dt – время прохождения лучом расстояния ds. Тогда из (1.5) следует, что оптическая длина пути между двумя точками Р1 и Р2, лежащими на одном луче, равна

, (1.6)

т. е. оптический путь между двумя точками равен скорости света в вакууме, умноженной на время прохождения лучом расстояния между этими точками.

Уравнение светового луча в неоднородной среде

Обсудим более детально характер искривления лучей в неоднородной среде. Будем рассматривать радиус-вектор r точки P, лежащей на луче, как функцию длины дуги луча s (рис. 1.3). Тогда и уравнение эйконала запишется в виде . Продифференцируем это уравнение по длине дуги s, учитывая, что , получаем

. (1.6)

Поскольку вторая производная от радиус-вектора характеризует кривизну луча, из (1.6) следует, что в неоднородной среде световые лучи изгибаются в сторону увеличения показателя преломления. Этот вывод согласуется с ходом лучей на рис. 1.1.

Искривлением световых лучей в неоднородной среде объясняется появление миражей. Нижние миражи (рис. 1.4а) обусловлены тем, что слои воздуха, прилегающие к нагретой поверхности песка в пустыне имеют меньшую плотность (а значит и меньший показатель преломления), в результате возникает изображение удаленных предметов, как при отражении в зеркале. К этому же типу оптической иллюзии относится известный всем автомобилистам эффект зеркальных “луж” на нагретом асфальте.

Для возникновения так называемого верхнего миража (рис. 1.4б) необходимо, чтобы показатель преломления приповерхностного слоя воздуха достаточно быстро уменьшался с высотой, что возможно, когда, например, внизу располагается холодный слой, а над ним находится слой более теплого воздуха.

Эффект атмосферной рефракции возникает из-за искривления световых лучей при наклонном прохождении верхних слоев атмосферы (рис. 1.4в). Благодаря этому Солнце остается видимым еще некоторое время после ухода под горизонт, а видимые положения небесных светил смещаются относительно истинных в сторону зенита.

Закон прямолинейного распространения света в однородных средах

Из уравнения (1.6) следует, что в однородной среде (n = const, grad n = 0) кривизна лучей равна нулю, т. е. свет распространяется прямолинейно. Этот закон может считаться прочно установленным на опыте, он встречается еще за 600 лет до нашей эры в сочинениях Фалеса Милетского. Он имеет глубокий смысл, ибо понятие о прямой линии, по-видимому, возникло из оптических наблюдений. Геометрическое понятие прямой как линии, представляющей кратчайшее расстояние между двумя точками, есть понятие о линии, по которой распространяется свет в однородной среде, образуя геометрические тени (рис. 1.5).

Закон интенсивности

Рассмотрим узкую трубку лучей, выходящих из элемента dS1 волнового фронта L = a1 и пусть dS2 – элемент, который пересекают эти лучи на другом волновом фронте L = a2 (рис. 1.6). Поскольку направление вектора Пойнтинга в каждой точке трубки совпадает с направлением луча, полная энергия, протекающая по трубке постоянна и не зависит от изменения ее сечения: W1 = W2. Тогда интенсивности I1 и I2 в двух сечениях связаны соотношением , выра­жающим закон интенсивности в геометрической оптике: произведение IdS остается постоянным вдоль трубки лучей. В частном случае, если пучок прямолинейных лучей выходит из одной точки, а волновые фронты имеют вид сферических поверхностей, интенсивность света оказывается обратно пропорциональной квадрату расстояния от источника.

Закон независимости световых пучков

Закон независимости включает в себя два положения: а) если световой пучок разбить на отдельные пучки с помощью диафрагм, то действие на экране этих выделенных пучков оказывается независимым от того, действуют ли одновременно другие пучки, или они устранены; б) распространение всякого светового пучка в среде совершенно не зависит от того, есть в ней другие пучки света или нет. Закон независимости световых пучков необходимо дополнить утверждением, определяющим совместное действие световых пучков при попадании их на освещаемую поверхность: освещенность экрана, создаваемая несколькими световыми пучками, равна сумме освещенностей, создаваемых каждым пучком в отдельности. Нарушения справедливости этого утверждения имеют место в нелинейной оптике или при интерференции света.

В первом случае интенсивность пучков столь велика, что их совместное действие меняет свойства среды и поведение пучков в зоне перекрытия отличается от поведения в других областях. Во втором случае взаимная сфазированность электромагнитных волн приводит к перераспределению интенсивности света во времени и пространстве.

Стигматические световые пучки

Пользуясь представлениями лучевой (геометрической) оптики предполагается рассматривать каждую светящуюся точку источника света как вершину расходящегося пучка лучей, называемого гомоцентрическим, т. е. имеющим общий центр. Если после отражения или преломления света на границах раздела сред этот пучок превращается в пучок, сходящийся тоже в одну точку, то и последний представляет собой гомоцентрический пучок и центр его является изображением светящейся точки. При сохранении гомоцентричности каждая точка источника дает одну точку изображения (сопряженную). Такие изображения называются точечными или стигматическими (рис. 1.7).

В силу обратимости (взаимности) световых лучей (см. ниже) изображение можно рассматривать как источник, а источник — как изображение. Поэтому при стигматическом изображении центры пучков называются сопряженными точками той оптической системы, в которой происходит преобразование расходящегося гомоцентрического пучка в сходящийся. Соответственные лучи и пучки также называются сопряженными. Если в результате отражения и преломления пучок перестает быть гомоцентрическим, то стигматичность изображения теряется, и точка уже не изображается точкой. Так как в практической оптике обычно ставится задача получения изображений, точно передающих форму источника, то важнейшим вопросом геометрической оптики является выяснение условий сохранения гомоцентричности пучков.

1.4 Принцип Ферма

Найдем величину оптического пути между двумя точками А и В, лежащими на одном луче (рис. 1.8):

.

Этот интеграл, равный разности значений эйконала в точках В и А и, следовательно, не зависящий от пути интегрирования, называется интегральным инвариантом Лагранжа. Но , поэтому

. Знак равенства имеет место только в том случае, когда направления векторов s и dr совпадают в каждой точке траектории, т. е. когда она представляет собой реальный световой луч (АСВ на рис. 1.8). Для любой другой траектории, соединяющей точки А и В (например, ADB) оптическая длина пути оказывается больше, чем для реального луча.

Обобщением вышеприведенных рассуждений является принцип Ферма: свет распространяется по такой траектории, оптическая длина которой (а значит и время распространения) имеет экстремальное значение (минимальное, максимальное или стационарное) в некоторой регулярной окрестности светового луча. Под регулярной окрестностью понимается область, которую можно заполнить световыми лучами так, что через каждую точку будет проходить единственный луч. В большинстве случаев оптическая длина луча принимает минимальное значение, поэтому этот принцип называют также принципом наикратчайшего оптического пути.

В формулировке минимального светового пути этот принцип был выдвинут еще Героном Александрийским в III веке до н. э., а в формулировке минимального времени – в XVII веке Пьером Ферма.

Иллюстрация применения принципа Ферма к отражению света от поверхностей различной кривизны показан на рис. 1.9. Нетрудно доказать, что для плоской (рис. 1.9а) и выпуклой (рис. 1.9б) поверхностей из всех возможных траекторий АКВ, соединяющих точки А и В, таких, что точка К лежит на зеркале, наименьшую длину, имеет та, для которой угол падения равен

углу отражения.

Для эллиптического зеркала, у которого точки А и В являются фокусами, сумма длин отрезков АК и КВ постоянна. Поэтому оптическая длина траектории АКВ имеет стационарное значение и все реальные лучи, вышедшие из А, попадают в В. Точка В является изображением точки А, т. е. А и В – сопряженные точки. Этот пример иллюстрирует закон таутохронизма (одновременности): оптическая длина лучей между двумя сопряженными точками постоянна.

В случае когда отражение света происходит от вогнутой поверхности с кривизной большей, чем у эллипса, оптическая длина реального луча максимальна по сравнению с соседними лучами (рис. 1.9г).

Принцип Ферма может рассматриваться как основополагающий принцип геометрической оптики. Из него, так же как из уравнения эйконала, могут быть получены такие важнейшие следствия, как например

— закон прямолинейного распространения света в однородной среде;

— законы отражения и преломления на границах раздела, т. е. на тех поверхностях, где показатель преломления меняется скачком;

— траектории распространения световых лучей в неоднородной среде с непрерывно изменяющимся показателем преломления;

— закон взаимности или обратимости светового луча, в соответствии с которым траектории всех лучей, остаются без изменения при изменении их направлений распространения на противоположные.

1.5 Прохождение света через плоскую границу раздела

Предположим, что световой пучок распространяется в среде, показатель преломления которой плавно изменяется, но зависит только от одной координаты: n = n(z). Поскольку в плоскости XY показатель преломления остается постоянным, такие среды называются плоско-слоистыми. Исходя из уравнения эйконала, можно показать, что каждый световой луч в этом случае является плоской кривой, а угол q, который луч образует с осью OZ, удовлетворяет справедливому для любых зависимостей n(z) соотношению

. (1.7)

На рис. 1.10 показано распространение лучей, испущенных точечным источником, помещенным в плоско-слоистую среду. Рис. 1.10а соответствует случаю убывания функции n(z), 1.10б – возрастанию, а 1.10в – наличию минимума показателя преломления. Если луч распространяется в сторону уменьшения показателя преломления, он может углубиться в среду только на определенное расстояние, дойдя до точки поворота zп. Поскольку в точке поворота луча q = p/2 и sinq = 1, то zп определяется из соотношения , где q0 – угол выхода луча из источника, n0 – показатель преломления в месте расположения источника.

Частным, но практически наиболее важным случаем плоско-слоистых сред являются две однородные среды с показателями преломления n1 и n2 с плоской границей раздела между ними. Ось Z направлена по нормали к границе раздела.

При прохождении через такую границу раздела свет испытывает отражение и преломление (рис. 1.11). Рисунок соответствует ситуации, когда показатель преломления первой среды меньше, чем второй (n1 V2). Взаимное расположение лучей описывается законами отражения и преломления света на границе раздела. Эти законы подробно обсуждаются далее (см. Оптика, ч. 3, разделы 5.1…5.3), поэтому здесь приведем только основные формулировки.

Отражение света от границы раздела двух однородных сред

Как непосредственно вытекает из принципа Ферма и вышепреведенного анализа, луч падающий, нормаль к отражающей поверхности и луч отраженный лежат в одной плоскости (плоскости падения), которая определяется как плоскость, образованная падающим на границу раздела лучом и нормалью к границе, проведенной в точке падения луча (рис. 1.12). Углы между лучами и нормалью равны между собой: угол падения a равен углу отражения b. Установление этого закона связано с употреблением полированных металлических поверхностей (зеркал), известных уже в очень отдаленную эпоху. Построение изображения точечного источника S в плоском зеркале приведено на рис. 1.13а. В результате отражения формируется мнимое изображение S¢ источника, т. е. изображение, возникающее в точке пересечения продолжений отраженных лучей. Расстояние от зеркала до изображения b¢ равно расстоянию от источника до зеркала b.

На рис. 1.13б показано построение изображения протяженного объекта. Поскольку изображение объекта строится как совокупность изображений всех его точек, то результат для плоского зеркала очевиден: изображение получается равным, прямым и мнимым. При визуальном восприятии такого изображения правая и левая стороны как бы меняются местами.

Построение изображений в скрещенных зеркалах представлено на рис. 1.14. При отражении источника S в зеркале 1 образуется изображение S¢, которое, в свою очередь, служит источником для изображения S² в зеркале 2 (рис. 1.14а). С другой стороны, начиная построение с зеркала 2, получим изображения S²¢ и S²² (рис. 1.14б). Можно показать, что сам источник S и все формирующиеся изображения лежат на дуге одной окружности с центром в вершине зеркального угла. Кроме того, из простых геометрических соображений очевидно, что угол d между направлениями лучей до и после отражения от двух зеркал равен удвоенному углу между зеркалами: .

Последнее свойство широко используется для конструирования уголковых отражателей света (рис. 1.15). Зеркала, образующие прямой угол, возвращают все световые лучи точно в обратном направлении.

Преломление света на границе раздела двух однородных сред

Правильная формулировка этого закона принадлежит Снеллиусу и доказывается принципом Ферма. Иллюстрацией этого принципа может служить первая задача к данному разделу. Согласно закону Снеллиуса (см. рис. 1.16), луч преломленный лежит в плоскости падения, а синусы углов падения и преломления связаны соотношением

, (1.8)

которое является частным случаем общего закона (1.7).

При прохождении луча сквозь плоскопараллельную пластинку направление прошедшего луча света совпадает с направлением падающего, однако луч смещается параллельно самому себе. Расстояние х, измеренное в направлении, поперечном лучу, носит название смещения луча (рис. 1.17). Оно пропорционально толщине пластинки d и зависит от ее показателя преломления.

Если луч идет из оптически более плотной среды в менее плотную (n2