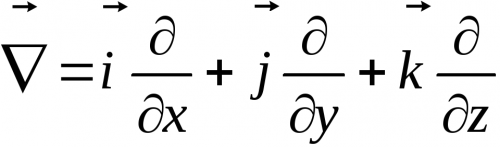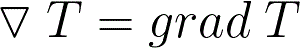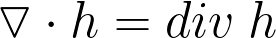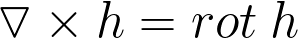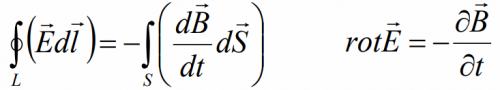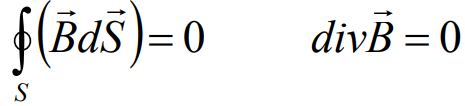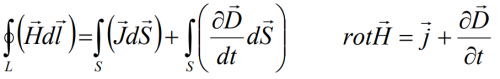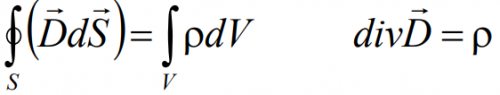Уравнения Максвелла

Уравнения Максвелла — это 4 уравнения, которые описывают, как электрические и магнитные поля распространяются и взаимодействуют; т.е. эти уравнения (правила или даже законы) описывают процессы/взаимодействия электромагнетизма.

Эти правила описывают, как проходит управление поведением электрических и магнитных полей. Уравнения Максвелла показывают, что электрический заряд (положительный и отрицательный):

1. Порождает электрическое поле (также если заряд изменяется со временем, то он вызывает появление электрического поля).
2. В дальнейшем он вызывает появление магнитного поля.

Уравнения Максвелла в дифференциальной форме

Уравнение 1: Закон Гаусса или Теорема Гаусса

Дивергенция электрического поля равняется плотности заряда. Существует вязь между электрическим полем и электрическим зарядом.

Дивергенция в физике показывает, насколько данная точка пространства является источником или потребителем потока поля.

Очень кратко: Электрические поля расходятся от электрических зарядов: электрический заряд создаёт поле вокруг себя и, таким образом, действует как источник электрических полей. Это можно сравнить с краном, который является источником воды.

Ещё закон Гаусса говорит о том, что отрицательные заряды действуют как сток для электрических полей (способ, как вода стекает через отверстие стока). Это означает, что линии электрического поля имеют начало и поглощаются при электрическом заряде.

Заряды с одинаковым знаком отталкиваются друг от друга, а противоположные заряды притягиваются друг к другу (если есть два положительных заряда, они будут отталкиваться; а если есть один отрицательный и один положительный, они будут притягиваться друг к другу).

Уравнение 2: Закон электромагнитной индукции (Закон Фарадея)

Можно создать электрическое поле, изменив магнитное поле.

Очень кратко: Закон Фарадея гласит, что изменяющееся магнитное поле внутри контура вызывает индуцированный ток, который возникает из-за силы или напряжения внутри контура. Это значит:

1. Электрический ток порождает магнитные поля, а эти магнитные поля (вокруг цепи) вызывают электрический ток.
2. Изменяющееся во времени магнитное поле вызывает распространение электрического поля.
3. Циркулирующее во времени электрическое поле вызывает изменение магнитного поля во времени.

Уравнение 3: Закон Гаусса для магнетизма

Дивергенция магнитного потока любой замкнутой поверхности равна нулю. Магнитного монополя не существует.

Закон Гаусса для магнетизма утверждает (очень кратко):

1. Магнитных монополей не существует.
2. Расхождение полей B или H всегда равно нулю в любом объёме.
3. На расстоянии от магнитных диполей (это круговой ток) магнитные поля текут по замкнутому контуру.

Уравнение 4: Закон Ампера

Магнитное поле создаётся с помощью тока или изменяющегося электрического поля.

Очень кратко: Электрический ток порождает магнитное поле вокруг тока. Изменяющийся во времени электрический поток порождает магнитное поле.

Уравнения Максвелла в интегральной и дифференциальной форме

Вспомним сначала в дифференциальной форме и следом будет в интегральной форме.

Уравнение 1: Закон Гаусса (Теорема Гаусса)

Это же уравнение в интегральной форме:

Поток вектора электрической индукции D через любую замкнутую поверхность равняется сумме свободных зарядов, охваченных этой поверхностью. Электрическое поле создаётся нескомпенсированными электрическими зарядами (это те, что создают вокруг себя своё собственное электрическое поле).

Уравнение 2: Закон электромагнитной индукции (Закон Фарадея)

И это же уравнение в интегральной форме:

Циркуляция вектора напряжённости Е вихревого электрического поля (по любому замкнутому контуру) равняется скорости изменения магнитного потока через площадь контура (S) с противоположным знаком.

Уравнение 3: Закон Гаусса для магнетизма

И это же уравнение в интегральной форме:

Силовые линии магнитного поля замкнуты, т.к. поток вектора индукции В магнитного поля через любую замкнутую поверхность равняется нулю.

Уравнение 4: Закон Ампера

И это же уравнение в интегральной форме:

Циркуляция вектора напряжённости Н магнитного поля по замкнутому контуру равняется алгебраической сумме токов, которые пронизывают этот контур. Магнитное поле создаётся не только током проводимости, но и переменным электрическим полем.

Электромагнитная индукция. Уравнения Максвелла для электромагнитного поля

Уравнения Максвелла для электромагнитного поля

1. Явление электромагнитной индукции

2. ЭДС индукции в движущемся проводнике

3. ЭДС индукции в неподвижном проводнике

4. Самоиндукция. Индуктивность

5. Взаимная индукция

6. Энергия магнитного поля в неферромагнитной изотропной среде

7. Работа по перемагничиванию ферромагнетика

8. Теория Максвелла

8.1. Первое уравнение Максвелла

8.2. Ток смещения. Второе уравнение Максвелла

8.3. Теорема Остроградского-Гаусса. Третье и четвёртое уравнения Максвелла

8.4. Полная система уравнений Максвелла

8.5. Частные случаи: стационарное поле; поле в свободном пространстве

1. Явление электромагнитной индукции

При перемещении проводника в магнитном поле под действием силы Ампера (рис.16.1) совершается работа (см. предыдущую лекцию)

. (16.1)

Эта работа совершается за счёт энергии источника. Полная работа источника равна

и по закону сохранения энергии расходуется и на перемещение проводника (16.1), и на нагрев проводников. Выделяющаяся теплота по закону Джоуля-Ленца равна

,

где R – полное сопротивление цепи; тогда

,

.

.

Последнее выражение представляет собой закон Ома для полной цепи, причём в числителе, кроме ЭДС источника, появилось ещё одно слагаемое, которое естественно интерпретируется тоже как ЭДС. Это – ЭДС индукции:

. (16.2)

Получен закон Фарадея: ЭДС индукции в замкнутом контуре равна по величине и противоположна по знаку скорости изменения магнитного потока через поверхность, натянутую на этот контур.

Знак «минус» в (16.2) является следствием закона сохранения энергии: если бы минуса не было, появившийся из-за ЭДС индукции дополнительный ток (индукционный ток ) провоцировал бы дальнейшее изменение магнитного потока, что вело бы опять же к увеличению индукционного тока и так до бесконечности, а такого быть не может – энергия для возросшего до бесконечности тока тоже требовалась бы бесконечная. Отсюда – правило Ленца: собственное магнитное поле индукционного тока препятствует изменению магнитного потока, вызвавшего индукционный ток.

Закон Фарадея (16.2) здесь получен для одного частного случая (деформации контура), но он универсален: ЭДС индукции можно вычислять по (16.2) независимо от того, каким способом изменяется магнитный поток :

1) можно деформировать контур (изменяем площадь);

2) перемещать контур (изменяем ориентацию контура в пространстве – угол );

3) изменять индукцию поля .

2. ЭДС индукции в движущемся проводнике можно объяснить возникновением силы Лоренца.

Пусть проводник длиной движется в плоскости, перпендикулярной индукции поля , и скорость направлена под углом к проводнику (рис.16.2).

Электроны проводника движутся вместе с проводником, и на них действует сила Лоренца

,

что эквивалентно действию поля сторонних сил с напряжённостью

.

Под действием силы Лоренца электроны проводника перемещаются вдоль проводника (вверх на рис.15.2). Между точками (1) и (2) на концах проводника возникает разность потенциалов.

ЭДС (в данном случае – ЭДС индукции) по определению равна

,

. (16.3)

То же самое можно получить по закону Фарадея (16.2). Площадь, заметённая проводником в процессе движения, равна

,

пересечённый магнитный поток

,

ЭДС индукции по (16.2)

.

3. ЭДС индукции в неподвижном проводнике

ЭДС индукции, возникающую в неподвижном проводнике при изменении индукции магнитного поля, объяснить силой Лоренца нельзя. Максвелл предположил, что всякое переменное магнитное поле порождает в пространстве электрическое поле , которое и является причиной возникновения индукционного тока. Поле неэлектростатического происхождения.

Если , то возникает поле . По аналогии с предыдущим случаем для любого замкнутого контура L, мысленно выделенного в пространстве:

.

По закону Фарадея:

,

где – изменение магнитного потока через поверхность, натянутую на контур L (рис.15.3).

По определению магнитного потока

,

.

Операции дифференцирования по времени и интегрирования по пространству независимы друг от друга, поэтому их можно поменять местами; при этом производная будет частной (по времени):

.

Как видно, циркуляция вектора отлична от нуля, то есть это поле вихревое, непотенциальное.

. (16.4)

Циркуляция напряжённости вихревого электрического поля , порождённого изменяющимся магнитным полем , по произвольному замкнутому контуру равна по величине и противоположна по знаку потоку производной индукции магнитного поля через поверхность, натянутую на этот контур.

4. Самоиндукция. Индуктивность

Контур с током I создаёт в окружающем пространстве магнитное поле, индукция которого пропорциональна силе тока: (рис.16.4).

Магнитный поток через поверхность, натянутую на контур, пропорционален индукции (по определению потока ):

.

Введём коэффициент пропорциональности между током в контуре и магнитным потоком – индуктивность контура L:

, (16.5)

. (16.5а)

Индуктивность контура численно равна магнитному потоку, пронизывающему контур, если сила тока в контуре равна 1 А.

Для катушки с N витками нужно учитывать суммарный магнитный поток сквозь все витки, то есть полное потокосцепление

, (16.6)

. (16.5б)

Индуктивность контура зависит от формы контура, его размеров и магнитных свойств среды. Размерность

.

Пример: индуктивность длинного соленоида.

Индукция поля длинного соленоида

,

где n – плотность намотки (число витков на единицу длины):

. (16.7)

Магнитный поток через сечение соленоида

.

.

,

. (16.8)

или, с учётом (16.7):

. (16.8а)

Поскольку – объём соленоида, то

. (16.8б)

Самоиндукция. Если в контуре изменяется сила тока, то пропорционально будет меняться и магнитный поток, что приведёт в возникновению ЭДС индукции в контуре (закон Фарадея). Это – явление самоиндукции. Самоиндукция – возникновение ЭДС индукции в контуре при изменении силы тока в нём.

.

Будем считать коэффициент самоиндукции L постоянным, тогда

. (16.9)

При замыкании или размыкании цепи токи резко меняются. Если индуктивность контура велика, то из-за возникновения ЭДС самоиндукции индукционный ток может быть много больше тока, на который рассчитана нагрузка:

.

Такие токи называются экстратоками замыкания или размыкания. Именно возникновение таких токов объясняет, почему лампочки чаще перегорают в момент включения или выключения.

5. Взаимная индукция

Рассмотрим два контура L1 и L2 с токами I1 и I2 соответственно, расположенные не слишком далеко друг от друга так, чтобы линии индукции B1 поля, созданного током I1 первого контура, пронизывали второй контур (рис.16.5).

Магнитный поток через второй контур пропорционален индукции B1 поля, созданного первым током, а индукция B1 пропорциональна току I1:

.

Введём коэффициент пропорциональности – коэффициент взаимной индукции двух контуров:

, (16.10)

. (16.10а)

И наоборот, если ток I2 во втором контуре создаёт поле с индукцией B2, то магнитный поток , пронизывающий первый контур, пропорционален току I2:

. (16.11)

Можно показать, что коэффициент пропорциональности в (16.10) и (16.11) один и тот же:

.

Коэффициент взаимной индукции зависит от формы, размеров обоих контуров, из взаимного расположения и магнитных свойств окружающей среды. Как и коэффициент самоиндукции, он измеряется в генри:

.

Пример: рассмотрим две катушки на общем ферромагнитном сердечнике (рис.16.6).

Число витков первой катушки равно N1, второй – N2; длина сердечника (тороида) по средней линии равна l, площадь сечения тороида – S. Линии индукции B1 магнитного поля, созданного током первой катушки, пронизывают все витки второй катушки, причём

;

магнитный поток через сечение сердечника

;

полное потокосцепление (суммарный поток через все N2 витков второй катушки) для второй катушки

;

а коэффициент взаимной индукции катушек

. (16.13)

Заметим, что для случая, когда поток, созданный одной катушкой, полностью проходит сквозь все витки второй катушки.

Если изменяется сила тока I1 в первом контуре, то по закону Фарадея и по (16.10) ЭДС индукции во втором контуре равна:

. (16.12)

Симметрично, при изменении тока во втором контуре ЭДС индукции в первом будет равна:

. (16.12а)

Явление взаимной индукции – это возникновение ЭДС индукции в одном контуре при изменении тока в другом контуре.

6. Энергия магнитного поля в неферромагнитной изотропной среде

При замыкании ключа К (рис.16.7) в цепи начинает течь ток и спустя некоторое время устанавливается его постоянное значение I, а в катушке – стационарное магнитное поле B. Будем считать, что сопротивление проводов и источника пренебрежимо мало (R=0), тогда по закону сохранения энергии работа источника идёт только на создание магнитного поля в соленоиде:

(16.14)

По второму правилу Кирхгофа для замкнутого контура:

.

ЭДС здесь две: ЭДС источника и ЭДС самоиндукции в катушке индуктивности:

.

,

Работа источника тока:

.

Отсюда энергия магнитного поля катушки

. (16.15)

По определению (16.5) , тогда

, (16.16)

. (16.17)

Если у катушки больше одного витка, нужно заменить поток на полное потокосцепление :

, (16.16а)

. (16.17б)

Эта энергия локализована в пространстве, где создано магнитное поле. Рассчитаем объёмную плотность энергии, считая поле однородным. По определению, объёмная плотность энергии – это энергия единицы объёма:

. (16.18)

Тогда из (16.15) и (16.8б):

.

Здесь в первых скобках – индукция поля соленоида; во вторых – напряжённость:

, (16.19)

. (16.20)

. (16.21)

Поскольку , можно записать по-другому:

, (16.22)

. (16.23)

7. Работа по перемагничиванию ферромагнетика

Имеется катушка с ферромагнитным сердечником. Ток в катушке периодически изменяется, ферромагнетик при этом перемагничивается. Изменения индукции B поля в ферромагнетике отстают от изменений напряжённости H, — возникает гистерезис (рис.16.8).

Работу по перемагничиванию ферромагнетика можно получить как произведение силы тока на изменение магнитного потока (точнее, полного потокосцепления в катушке):

. (16.1)

.

Из (16.20) заменим , тогда работа по перемагничиванию при изменении индукции на dB равна:

.

Работа в расчёте на единицу объёма:

. (16.24)

Она равна площади заштрихованной на графике (16.8) полоски. Работа по перемагничиванию единицы объёма ферромагнетика за один цикл равна площади петли гистерезиса, то есть интегралу:

. (16.25)

Чем уже петля гистерезиса (меньше коэрцитивная сила HC), тем меньше потери на перемагничивание; поэтому для изготовления сердечников электромагнитов применяют магнитомягкие ферромагнетики.

8. Теория Максвелла

Теория Максвелла для электромагнитного поля – это обобщение теоремы Остроградского-Гаусса, закона полного тока и закона электромагнитной индукции Фарадея. Теория решает задачу электродинамики: найти характеристики электрического и магнитного полей системы зарядов и токов.

8.1. Первое уравнение Максвелла

По теореме о циркуляции вектора напряжённости электроСТАТИЧЕСКОГО поля (то есть поля, созданного неподвижными зарядами):

.

По (16.4) циркуляция вектора напряжённости поля, созданного изменяющимся магнитным полем:

.

Поверхность S натянута на контур L (рис.16.9). Сложим почленно эти два уравнения:

,

где – напряжённость суммарного (полного) электрического поля. Тогда

. (I)

Это – первое уравнение Максвелла в интегральной форме. Его смысл: электрические поля создаются как электрическими зарядами, так и изменяющимся магнитным полем.

Дифференциальную форму первого уравнения Максвелла можно получить, если воспользоваться математической теоремой Стокса: для любого векторного поля (в том числе поля )

, (16.26)

где – ротор векторного поля; своего рода оператор векторного дифференцирования. Ротор проще всего записать в виде определителя:

. (16.27)

Таким образом, например, проекция ротора на ось OX равна:

.

Операция ротор – из той же серии, что и градиент:

;

Градиент конструирует из скалярного поля векторное, а ротор – из векторного снова векторное.

Градиент характеризует быстроту изменения величины (например, потенциала ) в пространстве. Смысл ротора (ротор – значит «вихрь»): если поле вихревое (непотенциальное), то его ротор отличен от нуля. Ротор показывает вихревой характер поля.

Из сравнения (16.26) и (I):

. (I)

Это – первое уравнение Максвелла в дифференциальной форме.

8.2. Ток смещения. Второе уравнение Максвелла

Изменяющееся во времени магнитное поле порождает возникновение вихревого электрического поля – это одно из предположений Максвелла. Второе предположение симметрично: изменяющееся во времени электрическое поле порождает возникновение магнитного поля. Это удобно описывать с помощью токов смещения. Рассмотрим протекание переменного тока через конденсатор (рис.16.9).

Внутри конденсатора реально никаких токов нет; а есть изменяющееся во времени электрическое поле – за счёт изменяющегося заряда обкладок конденсатора. Но предположим, что внутри конденсатора течёт ток смещения . Он должен быть равен току проводимости в подводящих проводах; таким образом ток будет непрерывным. Тогда

,

.

Здесь – поверхностная плотность заряда. В лекции 12 было показано, что вектор электрического смещения вблизи проводника равен поверхностной плотности заряда:

,

.

Здесь производная – частная, поскольку D зависит в общем случае ещё и от координат, а производная – по времени. Тогда плотность тока смещения равна:

. (16.28)

Особенности тока смещения:

1) Течёт в вакууме, где нет реальных заряженных частиц – переносчиков тока.

2) При протекании тока смещения не выделяется теплота Джоуля-Ленца.

3) Единственное положительное свойство (и назначение!) тока смещения – создавать магнитное поле.

Название «ток смещения» – из определения (16.28) через вектор электрического смещения .

Получим некоторые полезные соотношения для плотности тока смещения. Из лекции 12:

,

где – вектор поляризации диэлектрика, тогда

.

Первое слагаемое возникает в веществе при его поляризации и оправдывает термин «ток смещения»: в переменном электрическом поле происходит смещение поляризационных зарядов. Второе слагаемое есть и в вакууме, где никаких заряженных частиц нет.

Итак, в общем случае магнитные поля создаются токами проводимости и токами смещения. В законе полного тока (см. предыдущую лекцию)

заменим плотность тока проводимости на суммарную плотность тока проводимости и смещения:

,

тогда

, (II)

где S – поверхность, натянутая на контур L (рис.16.11).

Уравнение (II) – второе уравнение Максвелла для электромагнитного поля в интегральной форме.

Воспользовавшись теоремой Стокса (16.26) для напряжённости магнитного поля:

,

получим второе уравнение Максвелла в дифференциальной форме:

. (II)

Его смысл: магнитные поля создаются как токами проводимости (плотность тока проводимости – ), так и изменяющимися во времени электрическими полями – .

8.3. Теорема Остроградского-Гаусса. Третье и четвёртое уравнения Максвелла

Максвелл обобщил теорему Остроградского-Гаусса (см. лекцию 12) для любых полей, в том числе и нестационарных:

, (III)

где – объёмная плотность заряда. Интегрирование производится по объёму V, ограниченному замкнутой поверхностью S (рис.16.12).

Смысл теоремы: поток вектора электрического смещения через произвольную замкнутую поверхность равен алгебраической сумме электрических зарядов, охваченных этой поверхностью. Иначе говоря, источником электрического поля являются электрические заряды.

По математической теореме Гаусса:

, (16.29)

где – дивергенция векторного поля. Она равна по определению:

. (16.30)

Дивергенция завершает коллекцию операций дифференцирования по координатам векторных и скалярных полей: градиент из скаляра конструирует вектор ( – вектор), ротор из вектора снова даёт вектор, а дивергенция вектор превращает в скаляр ( – скаляр!). Сравнивая (16.30) и (III), получим третье уравнение Максвелла в дифференциальной форме:

. (III)

В лекции 14 сформулирована теорема Остроградского-Гаусса для магнитного поля:

. (IV)

Это – четвёртое уравнение Максвелла для электромагнитного поля в интегральной форме.

Аналогично в дифференциальной форме:

. (IV)

Смысл этого уравнения: магнитных зарядов нет.

8.4. Полная система уравнений Максвелла

Полная система уравнений Максвелла включает, кроме приведённых четырёх основных, ещё три так называемых материальных. Эти три связывают характеристики полей со свойствами среды и друг с другом и включают, в частности, закон Ома в дифференциальной форме. Вот полная система в интегральной и в дифференциальной формах:

8.5. Частные случаи: стационарное поле; поле в свободном пространстве

Если поля стационарные, все производные равны нулю:

Поля – магнитное и электрическое – разделяются. Их характеристики не связаны друг с другом.

Второй частный случай – поля в свободном пространстве, где нет ни зарядов, ни токов проводимости:

Рассмотрим систему двух первых уравнений Максвелла для свободного пространства:

или

Изменение магнитного поля порождает поле электрическое , тоже в общем случае изменяющееся во времени; а изменения поля порождают снова возникновение магнитного поля . Поля – электрическое и магнитное – распространяются, превращаясь друг в друга. Это – электромагнитная волна, распространяющаяся в свободном пространстве, в отрыве от первоначально породивших её зарядов и токов.

Уравнения Максвелла для электромагнитного поля — основные законы электродинамики

Система уравнений Максвелла обязана своим названием и появлением Джеймсу Клерку Максвеллу, сформулировавшему и записавшему данные уравнения в конце 19 века.

Максвелл Джемс Кларк (1831 — 1879) был известным британским физиком и математиком, профессором Кембриджского университета в Англии.

Он практически объединил в своих уравнениях все накопленные к тому времени экспериментально полученные результаты касательно электричества и магнетизма и придал законам электромагнетизма четкую математическую форму. Основные законы электродинамики (уравнения Максвелла) были сформулированы в 1873 году.

Максвелл развил учение Фарадея об электромагнитном поле в стройную математическую теорию, из которой вытекала возможность волнового распространения электромагнитных процессов. При этом оказалось, что скорость распространения электромагнитных процессов равна скорости света (величина которой была уже известна из опытов).

Это совпадение послужило для Максвелла основанием к тому, чтобы высказать идею об общей природе электромагнитных и световых явлений, т.е. об электромагнитной природе света.

Созданная Джеймсом Максвеллом теория электромагнитных явлений нашла первое подтверждение в опытах Герца, впервые получившего электромагнитные волны.

В итоге эти уравнения сыграли главную роль в формировании точных представлений классической электродинамики. Уравнения Максвелла могут быть записаны в дифференциальной или интегральной форме. Практически они описывают сухим языком математики электромагнитное поле и его связь с электрическими зарядами и токами в вакууме и в сплошных средах. К данным уравнениям можно добавить выражение для силы Лоренца, в этом случае мы получим полную систему уравнений классической электродинамики.

Чтобы понимать некоторые математические символы, использующиеся в дифференциальных формах уравнений Максвелла, для начала определим такую занятную вещь, как оператор набла.

Оператор набла (или оператор Гамильтона) — это векторный дифференциальный оператор, компоненты которого являются частными производными по координатам. Для нашего реального пространства, которое является трехмерным, адекватна прямоугольная система координат, для которой оператор набла определяется следующим образом:

где i, j и k – единичные координатные векторы

Оператор набла, будучи применен к полю тем или иным математическим образом, дает три возможные комбинации. Данные комбинации именуются:

Градиент — вектор, своим направлением указывающий направление наибольшего возрастания некоторой величины, значение которой меняется от одной точки пространства к другой (скалярного поля), а по величине (модулю) равный скорости роста этой величины в этом направлении.

Дивергенция (расхождение) — дифференциальный оператор, отображающий векторное поле на скалярное (то есть, в результате применения к векторному полю операции дифференцирования получается скалярное поле), который определяет (для каждой точки), «насколько расходится входящее и исходящее из малой окрестности данной точки поле», точнее, насколько расходятся входящий и исходящий потоки.

Ротор (вихрь, ротация) — векторный дифференциальный оператор над векторным полем.

Теперь рассмотрим непосредственно уравнения Максвелла в интегральной (слева) и дифференциальной (справа) формах, содержащие в себе основные законы электрического и магнитного полей, включая электромагнитную индукцию.

Интегральная форма: циркуляция вектора напряженности электрического поля по произвольному замкнутому контуру прямо пропорциональна скорости изменения магнитного потока через площадь, ограниченную этим контуром.

Дифференциальная форма: при всяком изменении магнитного поля возникает вихревое электрическое поле, пропорциональное скорости изменения индукции магнитного поля.

Физический смысл: всякое изменение магнитного поля во времени вызывает появление вихревого электрического поля.

Интегральная форма: поток индукции магнитного поля через произвольную замкнутую поверхность равен нулю. Это означает, что в природе нет магнитных зарядов.

Дифференциальная форма: поток силовых линий индукции магнитного поля из бесконечного элементарного объёма равен нулю, так как поле вихревое.

Физический смысл: источники магнитного поля в виде магнитных зарядов в природе отсутствуют.

Интегральная форма: циркуляция вектора напряженности магнитного поля по произвольному замкнутому контуру прямо пропорциональна суммарному току, пересекающему поверхность, охватываемую этим контуром.

Дифференциальная форма: вокруг любого проводника с током и вокруг любого переменного электрического поля существует вихревое магнитное поле.

Физический смысл: протекание тока проводимости по проводникам и изменения электрического поля во времени приводят к появлению вихревого магнитного поля.

Интегральная форма: поток вектора электростатической индукции через произвольную замкнутую поверхность, охватывающую заряды, прямо пропорционален суммарному заряду, расположенному внутри этой поверхности.

Дифференциальная форма: поток вектора индукции электростатического поля из бесконечного элементарного объема прямо пропорционален суммарному заряду, находящемуся в этом объёме.

Физический смысл: источником электрического поля является электрический заряд.

Система данных уравнений может быть дополнена системой так называемых материальных уравнений, которые характеризуют свойства заполняющей пространство материальной среды: