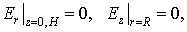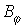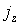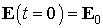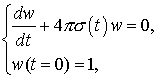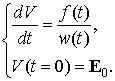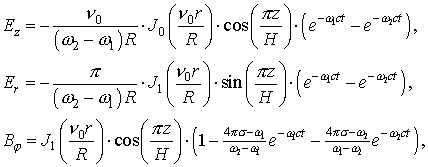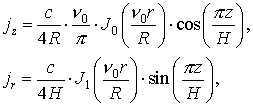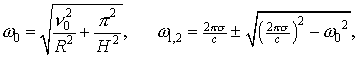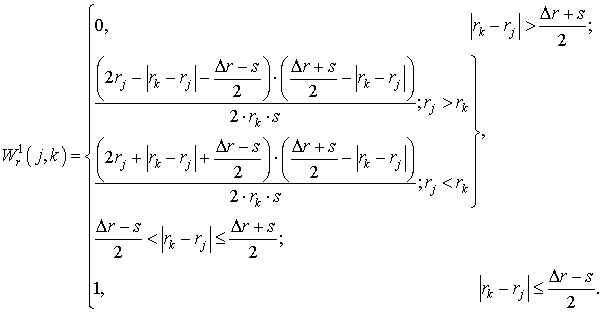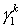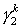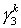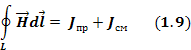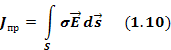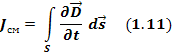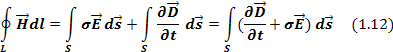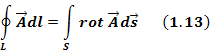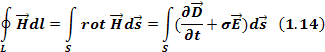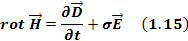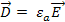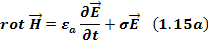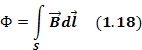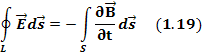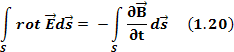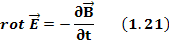Численное моделирование возбуждения электромагнитных полей в цилиндрической полости потоком релятивистских электронов
( Numerical Simulation of Electromagnetic Fields Generation in the Cylindrical Cavity by Relativistic Electron Flux
Preprint, Inst. Appl. Math., the Russian Academy of Science)
Егорушкин А.А., Крюков А.А., Скачков М.В.
(A.A.Yegorushkin, A.A.Krukov, M.V.Skachkov)
ИПМ им. М.В.Келдыша РАН
Москва, 2005
Аннотация
Рассмотрен эксперимент, в котором аксиально-симметричный поток релятивистских электронов инжектируется с торца в цилиндрическую камеру (материал – Fe), заполненную воздухом. Математическая модель эксперимента включает двумерные нестационарные уравнения Максвелла в цилиндрических координатах; уравнения для вычисления проводимости воздушной среды в камере; моделирование потока релятивистских электронов методом крупных частиц. При численном интегрировании уравнений Максвелла используется идеология метода квазианалитической интерполяции. В методе крупных частиц расчёт плотности тока основывается на законе сохранения заряда в ячейках. Предложен и реализован подход к распараллеливанию вычислительного алгоритма на многопроцессорной вычислительной технике с распределённой памятью, который принципиально отличается от геометрического распараллеливания и использует тот факт, что моделирование крупных частиц занимает основное расчётное время.
Abstract
The experiment, which is in the axial-symmetric relativistic electron flux injecting from the end face into the cylindrical chamber (material – Fe) filled with the air, is considered. The mathematical model contains the 2-D non-stationary Maxwell equations in cylindrical coordinate system, the equations for computing the air conductivity in the chamber and the particle simulation algorithm for the relativistic electron flux. For integrating the Maxwell equations the quasianalitic interpolation technique is used. The computation of the current density that is realized in the particle simulation algorithm is based on the charge conservation in grid cells. The technique of the parallel computations at multiprocessor with distributed memory is proposed. This technique is different from the geometric method and uses the fact that the particle simulation algorithm occupies the basic time of computations.
Возбуждение электромагнитных полей в полостях технологических объектов, находящихся под воздействием гамма-излучения, определяется комптоновской ионизацией материалов. В результате ионизации возникает поток комптоновских электронов высоких энергий, который, в свою очередь, взаимодействует с молекулами нейтрального газа, заполняющего полости, и образует потоки вторичных электронов. Возникающие при этом электромагнитные колебания влияют на функционирование электронной аппаратуры объектов.
Разработка адекватной математической модели указанных физических процессов и построение вычислительных алгоритмов в сложной геометрии является нетривиальной задачей. В связи с этим актуальными становятся разработка и исследование математических моделей конкретных физических экспериментов, построение численных методик расчёта электромагнитных полей и проведение на их основе численного эксперимента. Численный эксперимент позволит более детально изучать отдельные этапы эволюции физических процессов и путём сравнения с результатами физических экспериментов выбрать адекватную математическую модель.
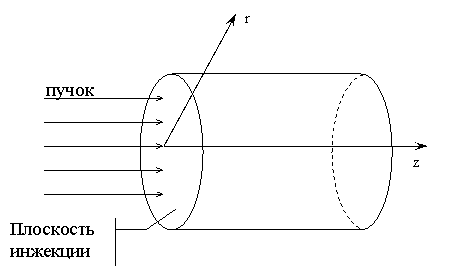
В настоящей работе рассматривается эксперимент, в котором аксиально-симметричный поток гамма-квантов проникает сквозь торец в цилиндрическую камеру (материал – Fe ), заполненную воздушной средой. Ось потока совпадает с осью камеры. Процесс взаимодействия гамма-квантов с торцом камеры и образование потока комптоновских релятивистских электронов моделируется методом Монте – Карло [1], его описание выходит за рамки настоящей работы. В работе этот поток считается заданным, т. е. в камеру инжектируется аксиально-симметричный пучок релятивистских электронов.
Математическая модель рассматриваемого эксперимента включает три взаимосвязанные подзадачи.
1. Задача для двумерных нестационарных уравнений Максвелла в цилиндрических координатах с граничными и начальными условиями.
2. Вычисление проводимости воздушной среды в камере.
3. Моделирование потока релятивистских электронов методом крупных частиц.
При численной реализации модели были решены следующие проблемы.
Во-первых, в зависимости от интенсивности потока релятивистских электронов возможны процесс лавинной ионизации воздушной среды в камере и, как следствие, большая проводимость. Поэтому численные методики интегрирования уравнений Максвелла и уравнений для вычисления проводимости должны быть адаптированы к этим процессам. В настоящей работе для этой цели используется идеология метода квазианалитической интерполяции [2].
Во-вторых, стандартные процедуры вычисления плотности тока в методе крупных частиц не обеспечивают сохранение заряда в ячейках, что в случае малой проводимости воздушной среды может привести к накоплению фиктивного заряда в расчётной области и заметному искажению электрического поля [3]. Поэтому в работе предлагается методика расчёта плотности тока, основанная на законе сохранения заряда в ячейках.
В-третьих, в силу цилиндрической симметрии расчётной сетки возникает проблема со взвешиванием заряда частиц вблизи оси симметрии. Стандартные процедуры взвешивания не дают удовлетворительного результата в осевых ячейках. Простая интерполяция из соседних не осевых ячеек не годится, так как требуется выполнение закона сохранения заряда в ячейках. В работе предлагается процедура взвешивания, дающая правильный результат в осевых ячейках.
В-четвёртых, предложен и реализован подход к распараллеливанию вычислительного алгоритма, который принципиально отличается от геометрического распараллеливания и использует тот факт, что моделирование крупных частиц занимает основное расчётное время.
§1. Математическая модель
Рассматривается эксперимент, в котором аксиально-симметричный пучок релятивистских электронов инжектируется в цилиндрическую камеру, заполненную нейтральной воздушной средой (рис.1). Ось пучка совпадает с осью камеры. Давление в камере Р=1атм. Математическая модель эксперимента включает следующие взаимосвязанные подзадачи.
SHAPE \* MERGEFORMAT
1. Уравнения Максвелла в цилиндрических координатах с граничными и начальными условиями:
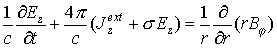
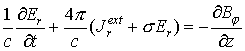
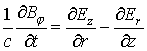
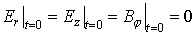
2. Уравнения движения релятивистских электронов
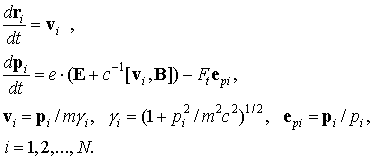
Начальные координаты электронов распределены в плоскости инжекции ( z = 0) равномерно по сечению. Начальные скорости отвечают энергетическому спектру электронов в пучке. Сила ионизационного торможения Ft описывается формулой Бета – Блоха:
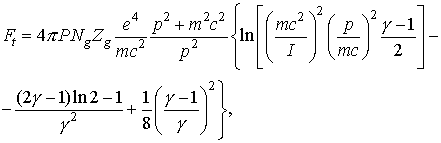
где Р – давление в атм., 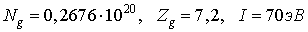

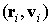
3. Уравнения для вычисления проводимости воздушной среды в камере:
где n – концентрация электронов проводимости, Q ( t ) – источник вторичной ионизации (вычисляется с использованием метода крупных частиц), u ( P , E ) – подвижность электронов проводимости, a ( P , E ) – скорость вторичной ионизации (значения величин u ( P , E ) и a ( P , E ) посчитаны по методике, изложенной в работе [4], и содержатся в таблицах),
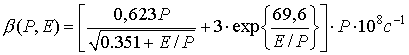
§2. Численное интегрирование уравнений Максвелла и уравнения для вычисления проводимости воздушной среды
Для разностной аппроксимации системы уравнений (1) используется вариант явной схемы «крест». Вводится равномерная сетка по времени 
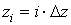
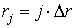
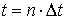
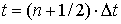
SHAPE \* MERGEFORMAT
SHAPE \* MERGEFORMAT

SHAPE \* MERGEFORMAT
SHAPE \* MERGEFORMAT
SHAPE \* MERGEFORMAT
Пространственные производные заменяются центрально-симметричными разностными соотношениями
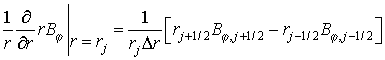

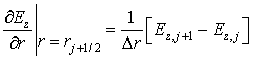
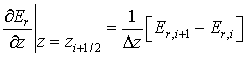
При интегрировании по времени используется идеология метода квазианалитической интерполяции [2]. Для аппроксимации дифференциального уравнения с начальным условием
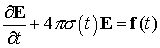
вводится вспомогательная функция 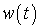
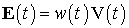
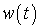
решив которую получим
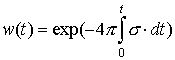
Тогда 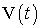
Интегрируя это уравнение и аппроксимируя интеграл по времени, получим разностную запись исходного уравнения
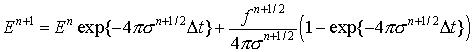
Такой метод обеспечивает первый порядок аппроксимации по D t в пределе 
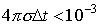
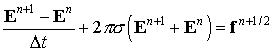
Была рассчитана следующая тестовая задача:
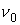
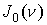
Метод квазианалитической интерполяции используется также при интегрировании уравнения (4):
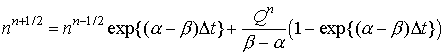
Необходимость в использовании квазианалитической интерполяции диктуется тем обстоятельством, что при E > 100 СГСЕ значение a велико.
§3. Моделирование потока релятивистских электронов методом крупных частиц
Численное интегрирование уравнений движения (2) проводится по методу, аналогичному методу Бориса [5]:
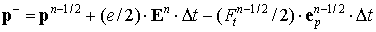

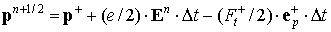
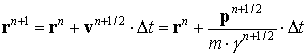
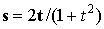
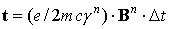
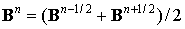
Здесь компоненты поля билинейно интерполированы с узлов пространственной сетки на координаты частиц. В алгоритме на каждом шаге по времени проводится проверка неравенства
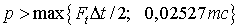
В случае нарушения этого неравенства электрон считается поглотившимся и его дальнейшее движение не рассматривается. Метод Бориса был выбран в связи с тем, что он полностью учитывает тот факт, что магнитное поле изменяет направление движения электрона, но не изменяет его энергию.
Метод крупных частиц, использованный для вычисления плотности тока 
3.1. Расчёт плотности тока в узлах расчётной сетки базируется на законе сохранения заряда в ячейках и основывается на методике работы [3]. Соблюдение закона сохранения заряда в ячейках особенно важно обеспечить в случае малой проводимости воздушной среды. В этом случае метод крупных частиц, не обеспечивающий сохранение заряда в ячейках, может привести к накоплению фиктивного заряда в расчётной области и заметному искажению электрического поля.
Стандартные процедуры вычисления плотности тока в узлах 
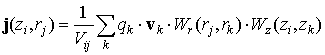
где 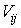
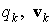
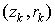
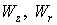
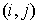
Эти процедуры не обеспечивают сохранение заряда в ячейках.
В работе предлагается другой алгоритм вычисления плотности тока, аналогичный алгоритму из [3]. В этом алгоритме производится подсчёт заряда, перенесённого каждой частицей через границу пространственной ячейки за один шаг по времени. Полученные значения суммируются по частицам, делятся на площадь границы и приравниваются к плотности тока в узле расчётной сетки на границе ячейки.
Подсчёт заряда, перенесённого одной частицей через границу ячейки за один шаг по времени, проводится следующим образом. Предположим, что частица находится в ячейке 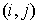
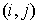
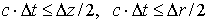
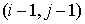
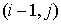
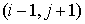

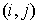
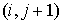
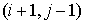
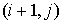
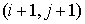
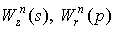
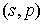

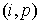
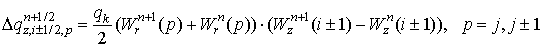
заряд, вынесенный из ячейки 
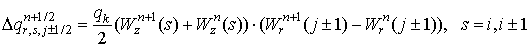
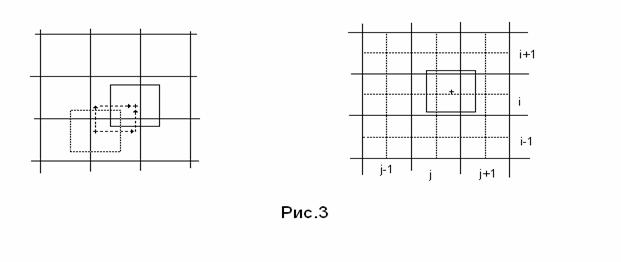
Предложенные формулы расчёта не являются единственно возможными. Они представляют собой полусумму результатов, полученных для двух вариантов движения частицы: смещение сначала параллельно оси z , а затем вдоль радиального направления до конечного положения частицы; смещение сначала вдоль радиального направления, а затем параллельно оси z (см. рис.3).
Для сглаживания электромагнитных шумов предложенный алгоритм вычисления плотности тока необходимо дополнить процедурой усреднения тока по характерному промежутку времени пролёта частицей пространственной ячейки [3]:
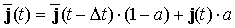
где 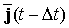
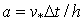
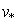
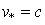
3.2. В силу цилиндрической симметрии возникает трудность, связанная с распределением заряда частиц вблизи оси. Кроме требования сохранения заряда частицы (7) форм-факторы должны обеспечивать правильный расчёт плотности тока в плоскости инжекции 
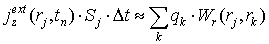
где 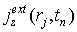
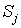
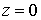

Начальные координаты электронов распределены в плоскости инжекции равномерно по r . Поэтому заряды инжектируемых частиц вычисляются по формуле:
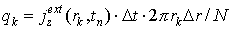
где N – число частиц, инжектируемых в одну ячейку за один шаг по времени. В пределе при 
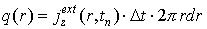
и в соотношении (8) суммирование заменяется интегрированием:
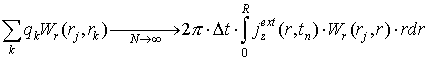
В предположении, что в пределах ячейки 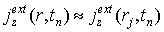
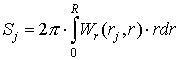
которому должна удовлетворять неотрицательная функция 
Рассмотрим два стандартных форм-фактора.
1. Взвешивание по модели CIC с равномерно заряженными крупными частицами.
2. Линейное взвешивание.
Здесь s – размер частицы. Функции 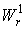
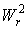
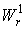
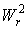
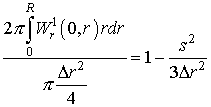
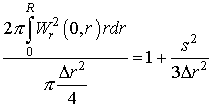
Из этих уравнений видно, что если в качестве искомой функции взять 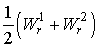
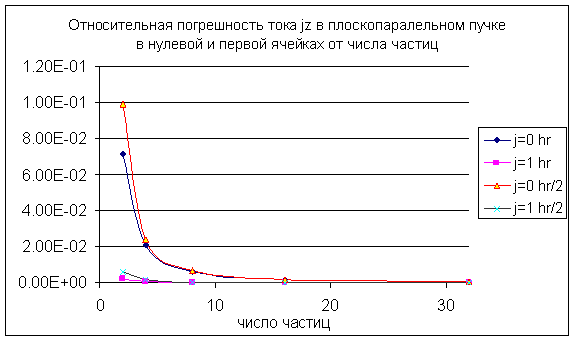
Ниже приведены расчетные данные для плоскопараллельного пучка (частицы движутся в направлении оси z ).
Использовались частицы размера hr и hr /2, 
2.3. Для сглаживания флуктуаций плотности тока, вызванных дискретной структурой пучка, целесообразно распределять начальные координаты и скорости частиц с использованием последовательности точек, равномерно распределённых в трёхмерном единичном кубе. При этом обычные случайные числа не годятся из-за их большой дисперсии при малой выборке. Удовлетворительные результаты даёт использование обращённых двоичных, троичных и пятеричных дробей 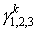
Последовательность точек 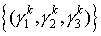
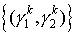
Опишем подробно процедуру инжекции крупных частиц в камеру в момент времени 
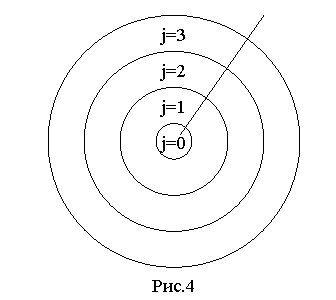
Пусть J – число ячеек в плоскости инжекции 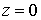
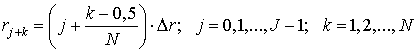
где N – число точек в пределах одной j -й ячейки. Число инжектируемых частиц увеличивается пропорционально номеру ячейки, т. е. с координатой 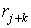
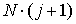
Начальные энергии и направления вылета электронов в j -й ячейке разыгрываются с использованием чисел 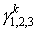
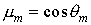
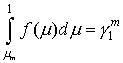
где 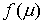
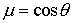
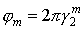
Начальная энергия электрона находится в результате решения уравнения:
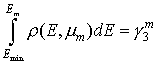
где 
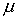

P – число шагов по времени между повторами в последовательности точек 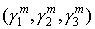
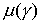
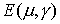
В связи с тем, что скорости электронов имели три компоненты, уравнения движения (2) интегрировались в декартовых координатах. Для расчёта плотности тока производился переход в цилиндрическую систему координат 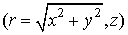

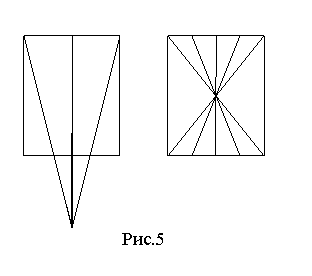
т. е. все частицы стартовали с одного луча. Такое описание применимо в аксиальной симметрии, когда точки на окружности 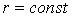
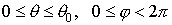
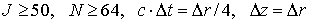
§4. Параллельная реализация вычислительного алгоритма на многопроцессорной вычислительной системе с распределённой памятью
Рассматриваемая в настоящей работе численная методика, реализующая метод крупных частиц, включает два основных блока:
1) решение уравнений Максвелла (1) сеточным методом и расчёт проводимости (4);
2) решение уравнений движения крупных частиц (2) (электронов пучка) и вычисление плотности тока пучка 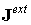
В процессе работы программы на каждом временном шаге блоки обмениваются данными. Этими данными являются массивы значений компонент электромагнитного поля, заполняемые в первом блоке и используемые во втором для решения уравнений движения электронов пучка, и плотность тока пучка 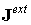
Просматриваются два основных подхода к распараллеливанию численной методики.
Первый подход – традиционное геометрическое распараллеливание. Расчётная область разбивается на подобласти, в каждой из которых за исключением границ задача решается самостоятельно. Эффективность распараллеливания существенно зависит от равномерности загрузки процессоров, обслуживающих разные подобласти. В связи с этим при реализации этого подхода возникает следующая трудность. Двум основным блокам численной методики требуются разные затраты временных ресурсов, которые отличаются на порядки. А именно, на моделирование движения частиц и их взвешивание на сетке требуется значительно больше времени, чем на разностное решение уравнений Максвелла. Это объясняется тем, что число крупных частиц много больше числа узлов пространственной расчётной сетки. В связи с этим равномерность загрузки процессоров жёстко связана с равномерностью распределения крупных частиц пучка в расчётной области. Однако в практических задачах ситуация усложняется тем, что пучок далеко не всегда занимает всю расчётную область. Он может находиться в некоторой её части и изменяться в пространстве и во времени (расширяться, сжиматься, деформироваться и т.п.).
Авторами настоящего препринта реализован второй подход к распараллеливанию численной методики, который использует тот факт, что моделирование крупных частиц занимает основное расчётное время. Число крупных частиц, приходящееся на одну пространственную ячейку, является дополнительной размерностью задачи. Поэтому если это число составляет сотни или тысячи единиц, то распараллеливание резонно проводить «по частицам», т.е. разделить всю совокупность крупных частиц на списки и распределить их по процессорам. Фактически это означает распараллеливание только второго блока численной методики, отвечающего за вычисление плотности тока пучка 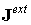
Организация обменных операций при распараллеливании «по частицам» принципиально отличается от геометрического распараллеливания. В геометрическом распараллеливании обмены осуществляются между двумя процессорами, обслуживающими соседние пространственные подобласти. В распараллеливании «по частицам» используются коллективные обмены.
Опишем схему организации обменов во втором подходе более детально. Пусть M – число процессоров, пронумерованных от 0 до ( M – 1). 0-ой процессор назовём головным ( root ). В головном процессоре реализуется первый блок численной методики, отвечающий за решение уравнений Максвелла. Выходными данными первого блока являются компоненты электромагнитного поля в узлах пространственной сетки, которые после вычисления на данном временном шаге распределяются по всем процессорам. Второй блок численной методики реализуется во всех процессорах, включая головной. Полный список крупных частиц пучка заранее разделён на M подобных списков, пучок расслаивается при этом на M одинаковых пучков. Процессор с номером i вычисляет плотность тока 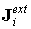
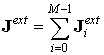
Затем происходит переход на следующий временной слой и алгоритм повторяется. Следует отметить, что такая схема организации обменов возможна благодаря тому, что частицы взаимодействуют друг с другом только на макро-уровне – через поле. Столкновения частиц не учитываются.
§5. Исходные данные и результаты расчётов
Результаты вычислительного эксперимента получены при следующих значениях исходных данных. Цилиндрическая камера (см. рис.1) имеет высоту H = 50 см и радиус R = 12,5 см . Плотность входного тока в плоскости инжекции z = 0 имеет вид:
где 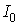
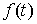
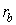
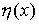
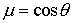

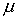

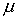
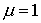
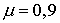
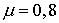
Основной расчёт проводился на 64 процессорах многопроцессорной вычислительной системы МВС-1000М и занял 220 мин. При этом на хранение текущей информации о координатах, импульсах и зарядах крупных частиц потребовалось по 150 Мбайт оперативной памяти на каждом процессоре. Таким образом, если бы тот же расчёт целиком проводить на одном процессоре, то потребовалось бы около 10 Гбайт оперативной памяти. Такой объём оперативной памяти не мог быть выделен одному процессору. Для оценки эффективности распараллеливания вычислительного алгоритма был проведён расчёт задачи на 32 процессорах. Общее время вычислений оказалось равным 410 мин, что указывает на то, что эффективность распараллеливания вычислений не менее 90%.
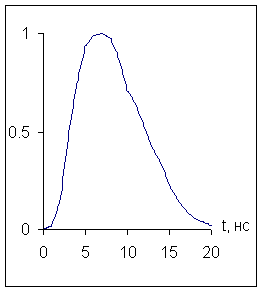
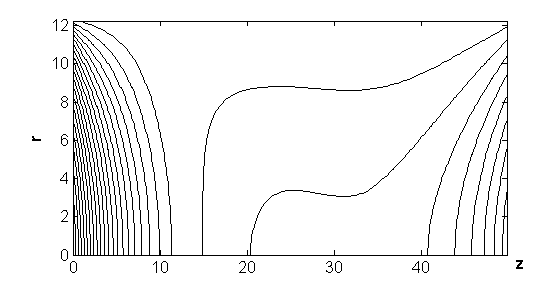
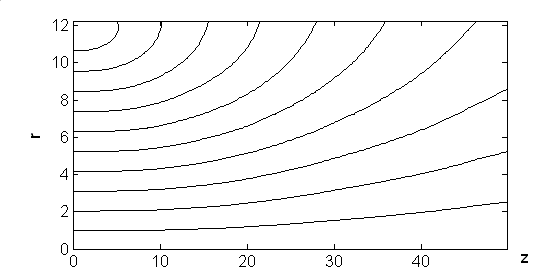
На рис.9 показаны линии уровня максимального по времени модуля z -компоненты напряжённости электрического поля 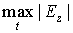
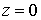

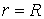
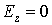
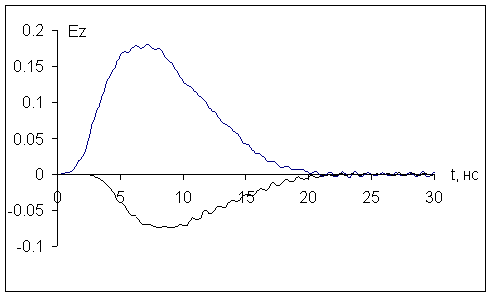
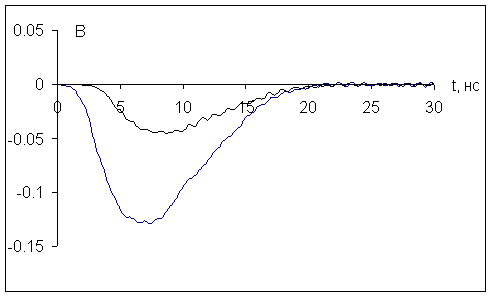
На рис.10 изображены зависимости от времени z -компоненты напряжённости электрического поля 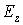
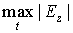
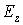
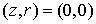
На рис.11 показаны линии уровня максимального по времени модуля напряжённости магнитного поля 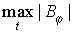
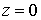
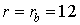
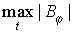
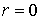
На рис.12 приведены зависимости от времени напряжённости магнитного поля в двух точках 
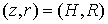
Приведённые результаты вычислительного эксперимента сравнивались с предварительными результатами физического эксперимента. Сравнение показало на удовлетворительное совпадение амплитуд электрического поля, полученных в физическом эксперименте, с результатами численных расчётов.
Авторы выражают признательность к. ф.-м. н. М. Е. Жуковскому за предоставленные исходные данные для вычислительного эксперимента, постоянное внимание и помощь в работе.
1. М.Е.Жуковский, С.В.Подоляко, Р.В.Усков. Алгоритм расчёта простран-ственного и спектрального распределений электронов, порождённых при взаимодействии проникающего излучения с объектами. М.: Ин. прикл. матем. им. М.В.Келдыша РАН, 2004, препр. №89, 16с.
2. В.Я.Арсенин, Г.Д.Васильков. О разностных схемах для дифференциаль-ных уравнений с диссипативными членами. – М.: Ин. прикл. матем. им. М.В.Келдыша АН СССР, 1981, препр. №17, 20с.
3. М.В.Скачков. О проблеме шумов и сохранения заряда в методе крупных частиц. // Матем. моделирование, 2000, т.12, №9, с.96-108.
4. А.В.Березин и др. О математических моделях вторичной ионизации. М.: Ин. прикл. матем. им. М.В.Келдыша РАН, 2002, препр. №29, 20с.
5. J.P.Boris. Relativistic Plasma Simulation-Optimization of a Hybrid Code // Proc. Fourth. Conf. Num. Sim. Plasmas, Naval Res. Lab., Wash D.C., 2-3 November 1970, p.3-67.
6. Ч.Бэдсэл, А.Ленгдон. Физика плазмы и численное моделирование. М.: Электроатомиздат, 1989, 455с.
Первое уравнение Максвелла.
Первое уравнение Максвелла — это обобщение закона Ампера и Био-Саварра для токов смещения. Звучит следующим образом: циркуляция вектора напряженности магнитного поля по замкнутому контуру равна полному току, пронизывающему этот контур.
В современном обозначении записывается
Т.о. физический смысл первого уравнения Максвелла состоит в том, что магнитное поле в некоторой области пространства связано не только с токами проводимости, протекающими в этой области, но и с изменением электрического поля во времени в этой области(токами смещения).
Это означает, что циркуляция вектора 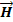

Уравнение 1.12 называют первым уравнением Максвелла в интегральной форме.
Получим дифференциальную форму уравнения Максвелла. Для этого воспользуемся уравнением Стокса, которое преобразует контурный интеграл в поверхностный:
Применим уравнение 1.13 к левой части уравнения 1.12. Получим
Уравнение 1.14 справедливо, если равны подынтегральные функции, то есть
Уравнение 1.15 есть первое уравнение Максвелла в дифференциальной форме.
Для изотропных сред
Подставим в 1.15
Дифференциальная форма первого уравнения Максвелла используется в том случае, когда производные поля по координатам пространства непрерывны. Интегральная форма 1.12 такого ограничения не имеет.
§1.3. Второе уравнение Максвелла.
Второе уравнение Максвелла— это обобщение закона индукции Фарадея для диэлектрической среды в свободном пространстве
где Ф – поток магнитной индукции, пронизывающий проводящий контур и создающий в нем ЭДС. ЭДС создается не только в проводящем контуре, но и в некотором диэлектрическом контуре в виде электрического тока смещения.
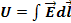
Физический смысл второго уравнения Максвелла состоит в том, что электрическое поле в некоторой области пространства связано с изменением магнитного поля во времени в этой области. То есть переменное магнитное поле возбуждает вихревое электрическое поле.
Получим второе уравнение Максвелла в интегральной форме
Уравнение 1.19 – второе уравнение Максвелла в интегральной форме.
Воспользуемся уравнением Стокса 1.13, преобразуем левую часть уравнения 1.19:
Уравнение 1.20 есть второе уравнение Максвелла в дифференциальной форме.
максвелла уравнения
МАКСВЕЛЛА УРАВНЕНИЯ
1. Краткая история
2. Каноническая форма
3. Максвелла уравнения в интегральной форме
4. Общая характеристика Максвелла уравнений
5. Максвелла уравнения для комплексных амплитуд
6. Алгебраические Максвелла уравнения
7. Материальные уравнения
8. Граничные условия
9. Двойственная симметрия Максвелла уравнений
10. Максвелла уравнения в четырёхмерном представлении
11. Лоренц-инвариантность Максвелла уравнений
12. Лагранжиан для электромагнитного поля
13. Единственность решений Максвелла уравнений
14. Классификация приближений Максвелла уравнений
15. Максвелла уравнения в различных системах единиц
Максвелла уравнения — ур-ния, к-рым подчиняется (в пределах применимости классической ыакроскопич. электродинамики, см. Электродинамика классическая), электромагнитное поле в вакууме и сплошных средах.
1. Краткая история
Установлению M. у. предшествовал ряд открытий законов взаимодействий заряженных, намагниченных и токонесущих тел (в частности, законов Кулона, Био — Савара, Ампера). В 1831 M. Фарадей (M. Faraday) открыл закон эл—магн. индукции и примерно в то же время ввёл понятие электрич. и магн. полей как самостоят, физ. субстанций. Опираясь на фарадеевское представление о поле и введя ток смещения, равнозначный по своему магн. действию обычному электрич. току, Дж. К. Максвелл (J. С. Maxwell, 1864) сформулировал систему ур-ний, названную впоследствии ур-ниями Максвелла. M. у. функционально связывают электрич. и магн. поля с зарядами и токами и охватывают собой все известные закономерности макроэлектромагнетизма. Впервые о M. у. было доложено на заседании Лондонского Королевского общества 27 окт. 18(34. Первоначально Максвелл прибегал к вспомогат. механич. моделям «эфира», но уже в «Трактате об электричестве и магнетизме» (1873) эл—магн. поле рассматривалось как самостоят, физ. объект. Физ. основа M. у.- принцип близкодействия, утверждающий, что передача эл—магн. возмущений от точки к точке происходит с конечной скоростью (в вакууме со скоростью света с). Он противопоставлялся ньютоновскому принципу дальнодействия, сводящемуся к мгновенной передаче воздействий на любое расстояние 
2. Каноническая форма
Канонич. форма записи, принятая ныне, принадлежит Г. Герцу (H. Hertz) и О. Хевисайду (О. Heaviside) и основана на использовании не кватернионных, а векторных полей: напряжённости электрического поля E, напряжённости магнитного поля H, векторов электрической индукции D и магнитной индукции В. M. у. связывают их между собой, с плотностью электрического заряда
Здесь использована Гаусса система единиц (о записи M. у. в др. системах см. в разделе 15). Входящие в (1) — (4) величины E, D, j являются истинными, или полярными, векторами (а величина r — истинным скаляром), поля H к В — псевдовекторами, или аксиальными векторами. Все эти величины предполагаются непрерывными (вместе со всеми производными) ф-циями времени t и координат 
3. Максвелла уравнения в интегральной форме
Используя Гаусса — Остроградского формулу и С такса формулу, ур-ниям (1) — (4) можно придать форму интегральных:
Криволинейные интегралы в (1a), (2a) берутся по произвольному замкнутому контуру (их наз. циркуляция-ми векторных полей), а стоящие в правых частях поверхностные интегралы — по поверхностям, ограниченным этими контурами (опирающимся на них), причём направление циркуляции (направление элемента контура


M. у. в форме (1a) — (4a) предназначаются не только для изучения топологич. свойств эл—магн. полей, но и являются удобным аппаратом решения конкретных задач электродинамики в системах с достаточно высокой симметрией или с априорно известными распределениями полей. Кроме того, в матем. отношении эта система ур-ний содержательнее системы (1) — (4), поскольку пригодна для описания разрывных, нодиффе-ренцируемых распределений полей. Но в отношении физ. пределов применимости обе системы ур-ний равнозначны, т. к. любые скачки полей в макроэлектродинамике должны рассматриваться как пределы микромасштабно плавных переходов, с тем чтобы внутри них сохранялась возможность усреднения ур-ний Лоренца — Максвелла. С этими оговорками резкие скачки можно описывать и в рамках M. у. (1) — (4), прибегая к аппарату обобщённых функций.
Наконец, M. у. в интегральной форме облегчают физ. интерпретацию MH. эл—магн. явлений и поэтому нагляднее сопоставляются с теми экспериментально установленными законами, к-рым они обязаны своим происхождением. Так, ур-ние (1a) есть обобщение Био — Савара закона (с добавлением к току 
Ур-ние (2a) выражает закон индукции Фарадея; иногда его правую часть переобозначают через «магн. ток смещения»
где

где 
4. Общая характеристика Максвелла уравнений
Совокупность M. у. (1) — (4) составляет систему из восьми (двух векторных и двух скалярных) линейных дифференц. ур-ний 1-го порядка для четырёх векторов 



или в интегральной форме:
Это ур-ние непрерывности для тока, содержащее в себе закон сохранения заряда для замкнутых изолнров. областей
Ур-ния (1) — (4) распадаются на два самостоят, «блока»: ур-ния (1) и (4), содержащие векторы 





Система M. у. (1) — (4) не является полной: по существу, она связывает 4 векторные величины двумя векторными ур-ниями. Её замыкание осуществляется путём добавления соотношений, связывающих векторы 1-го «блока»

5. Максвелла уравнения для комплексных амплитуд
В силу линейности системы (1) — (4) для её решений справедлив суперпозиции принцип .Часто оказывается удобным фурье-представление общего решения (1) — (4) как ф-ции времени (см. Фурье преобразование). Записывая временной фактор в виде 

Система (1б) — (4б) в нек-ром смысле удобнее (1) — (4), ибо упрощает применение к эл—динамич. системам, обладающим временной дисперсией (см. раздел 7), т. е. зависимостью параметров от частоты
6. Алгебраические Максвелла уравнения
Если распространить (в силу линейности M. у.) фурье-разложение и на зависимость полей от пространственных координат, т. е. представить общее решение ур-ний (1) — (4) в виде суперпозиции плоских волн типа 

Такое сведение M. у. к набору ур-ний для осцилляторов (осцилляторов поля) составляет важный этап перехода к квантовой электродинамике, где эл—магн. поле рассматривается как совокупность фотонов, характеризуемых энергиями 

7. Материальные уравнения
В макроэлектродинамике материальные связи, характеризующие эл—магн. свойства сред, вводятся феноменологически; они находятся либо непосредственно из эксперимента, либо на основании модельных представлений. Существуют два способа описания: в одном векторы E и H считаются исходными и материальные ур-ния задаются в виде D = D(E , H) и В = В( Е,Н), в другом — за исходные берутся векторы 2-го «блока» E и В, и соответствующие материальные связи представляются иначе: D = D(E,В), H= H(E, В). Оба описания совпадают для вакуума, где материальные уравнения вырождаются в равенства D = E и B = H.
Рассмотрим простейшую модель среды, характеризуемую мгновенным, локальным поляризац. откликом на появляющиеся в ней поля E и H. Под действием поля E в такой среде возникает электрич. поляризация 

Материальные ур-ния для таких сред имеют вид
При этом индуцированные в среде электрич. заряды наз. связанными или поляризац. зарядами с плотностью 

Эти понятия были перенесены и на магн. поля, что можно выразить в виде системы ур-ний, аналогичной
и только потом выяснилось, что истинными источниками намагничивания среды оказались электрич. токи 
тогда как следовало бы принять беззарядовые ур-ния
что равносильно замыканию исходных M. у. (1) — (4) с помощью материальных связей
Из (6) и (7a) следует, что 2-й вариант представления материальных соотношений, в к-ром постулируются в качестве исходных векторы E и B, физически предпочтительнее.
В модели Лоренца — Максвелла усреднение микрополя Нмикро, произведённое с учётом вклада со стороны индуциров. полей, приводит к ур-ниям (9) и соответственно = В. Однако обычно параметры сред вводятся с помощью ур-ний (7), что облегчает двойственную симметризацию ф-л (подробнее см. в разделе 9). Напр., скалярные восприимчивости сред (c e , c m ) определяются соотношениями
Простейшие модели сред характеризуются пост, значениями

Классификация разл. сред ооычно основывается на материальных ур-ниях типа (10) и их обобщениях. Если проницаемости e и m не зависят от полей, то M. у. (1) — (4) вместе с материальными ур-ниями (10) остаются линейными, поэтому о таких средах говорят как о линейных средах. При наличии зависимостей



Значение индуциров. поляризации Р е , напр, в момент г, может определяться, вообще говоря, значениями полей во все предыдущие моменты времени, т. е.
что при преобразовании Фурье по времени приводит к зависимости 




В проводящих средах входящая в M. у. (1) — (5) плотность тока 



где 




В общем случае вид материальных ур-ний зависит также и от системы отсчёта, в к-рой эти ур-ния рассматривают. Так, если в неподвижной системе К среда характеризуется простейшими ур-ниями (10), то в инер-циальной системе К’ , движущейся относительно К с пост, скоростью и, появляется анизотропия:
где индексы

что можно трактовать как наличие временной и пространственной дисперсии. Исследование процессов с материальными связями типа (12) составляет предмет электродинамики движущихся сред. Заметим, что хотя характеристики е и m удобно симметризуют материальные ур-ния, их введение не является непременным условием замыкания M. у. Соответствующей перенормировкой допустимо свести описание магн. поля к одно-векторному, т. е. сделать 

8. Граничные условия
Поскольку M. у. справедливы для любых (в рамках применимости макроэлектродинамики) неоднородных сред, то в областях резкого изменения их параметров иногда можно игнорировать тонкую структуру распределения полей в переходном слое и ограничиться «сшиванием» полей по разные стороны от него, заменяя тем самым переходный слой матем. поверхностью — границей, лишённой толщины. Если внутри переходной области имелись заряды с объёмной плотностью


Применение M. у. и ур-ния непрерывности приводит к следующим граничным условиям:
Здесь индексы 1 и 2 характеризуют поля по разные стороны от границы, а
Иногда граничные условия (1г) — (5г) порождают краевые условия, т. е. задают не правила перехода через границу, а сами поля на ней. Напр., внутри идеального проводника 






9. Двойственная симметрия Максвелла уравнений
Двойственная симметрия M. у. имеет место для любой формы их записи. Она состоит в инвариантности M. у. относительно линейных преобразований нолей, производимых по след, правилам:
Здесь








Таким сведением задач с заданными
Принцип перестановочной двойственности является представителем класса дискретных преобразований (см. Симметрия ),оставляющих инвариантными M. у. Такого же сорта преобразованиями являются, в частности, операция обращения времени
последовательно осуществляемые комбинации операций
10. Максвелла уравнения в четырёхмерном представлении
Придавая времени t смысл четвёртой координаты и представляя её чисто мнимой величиной 
где
аналогично вводят 4-вектор магн. тока.
В этих обозначениях M. у. допускают компактное 4-мерное представление:
Взаимной заменой векторов поля и индукции в ф-лах (13),
через к-рые также могут быть записаны M. у.:
Любая пара тензорных ур-ний, содержащая в правых частях оба 4-тока (электрич. и мат.), тождественна системе M. у. Чаще используют пару ур-ний (15 а), (18), при этом материальные ур-ния сводятся к функциональной связи между тензорами 

Из антисимметрии тензоров поля, индукции и M. у. в форме (17) — (18) следует равенство нулю 4-дивергенций 4-токов:
к-рое представляет собой 4-мерную запись ур-ний непрерывности для электрич. (магн.) зарядов. T. о., 4-векторы токов являются чисто вихревыми, и соотношения (17), (18) можно рассматривать как их представление в виде 4-роторов соответствующих тензоров. Наряду с представленным здесь вариантом часто используется также 4-мерное описание, в к-ром временная координата (обычно с индексом О) берётся действительной, но 4-мерному пространству приписывается гипербодич. сигнатура 
11. Лоренц-инвариантность Максвелла уравнений
Все экспериментально регистрируемые эл—динамич. явления удовлетворяют относительности принципу .Вид M. у. сохраняется при линейных преобразованиях, оставляющих неизменным интервал 







Релятивистски-ковариантная запись M. у. позволяет легко находить инвариантные комбинации полей, токов и потенциалов (4-скаляров или инвариантов Лоренца группы), сохраняющихся, в частности, при переходе от одной инерциальной системы отсчёта к другой. Во-первых, это чисто полевые инварианты (см. Инварианты электромагнитного поля ).Во-вторых, это токовые (источниковые) инварианты:
В-третьих, это потенциальные инварианты:
где



12. Лагранжиан для электромагнитного поля
M. у. могут быть получены из наименьшего действия принципа, т. е. их можно совместить с Эйлера — Лаг-ранжа уравнениями, обеспечивающими вариационную акстремальность ф-ции действия:
здесь 
В результате лагранжиан принимает вид инвариантной комбинации полей, потенциалов и источников:
А ур-ния Эйлера — Лагранжа для нек-рой обобщённой координаты 
Для 

13. Единственность решений Максвелла уравнений
Различают теоремы единственности для стационарных и нестационарных процессов. Условия единственности нестационарных решений извлекаются из Пойн-тинга теоремы, где источники считаются заданными ф-циями координат и времени. Если бы они порождали два разл. поля, то разность этих полей в вакууме (или в любой линейной материальной среде) вследствие принципа суперпозиции была бы решением однородных M. у. Для обращения этой разности в нуль и, следовательно, получения единств, решения достаточно удовлетворить след, трём условиям. 1) На поверхности S, окружающей область V, где ищется поле, должны быть заданы тангенциальные составляющие поля Е тан или поля Н тан либо соотношения между ними импедансного типа: 


В стационарных режимах нач. условия выпадают, и теоремы единственности формулируются непосредственно для установившихся решений. Так, в электростатике достаточно задать все источники r e ст , все полные заряды на изолиров. проводниках или их потенциалы, чтобы при соответствующих условиях на бесконечности (нужное спадание поля) решение было бы единственным. Аналогичные теоремы устанавливаются для магнитостатики и электродинамики пост, токов в проводящих средах.
Особо выделяется случай синусоидальных во времени процессов, для к-рых формулируют след, признаки, достаточные для получения единств, решения: 1) задание источников 
14. Классификация приближений Максвелла уравнений
Классификация приближений M. у. обычно основывается на безразмерных параметрах, определяющих и критерии подобия для эл—магн. полей. В вакууме таким параметром является отношение 


а) а = 0 — статич. приближение, статика.
Система M. у. распадается на три.
Материальная связь в простейшем случае имеет вид 



http://helpiks.org/6-65047.html
http://www.femto.com.ua/articles/part_1/2141.html