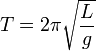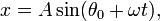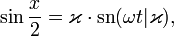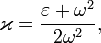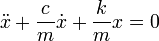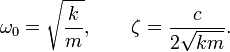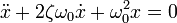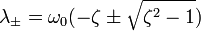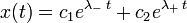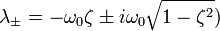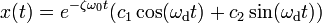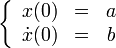Малые колебания физического и математического маятников
Физическим маятником называется твердое тело любой формы, имеющее горизонтальную ось вращения, не проходящую через центр тяжести тела, называемую осью привеса.
Рассмотрим движение физического маятника под действием силы тяжести Р (рис. 115). В соответствии с (111.218) дифференциальное уравнение движения физического маятника будет
где IO — момент инерции маятника относительно оси вращения О,
h — расстояние центра инерции С от оси вращения (длина физического маятника).
При малых колебаниях маятника или при малых углах отклонения φ можно принять sin φ ≈ φ, тогда
где
Интегрируя это уравнение, найдем
Постоянные интегрирования С1 и С2 определим из начальных условий движения. Например, пусть при t = 0, φ0=α, φ0=0.
Следовательно, под действием силы тяжести (без учета силы сопротивления среды) маятник совершает гармонические колебания. Частота этих колебаний
Период Т малых колебаний физичесйого маятника равен
Формула (111.222) может быть использована для опытного определения момента инерции твердого тела.
Математический маятник представляет собой несвободную тяжелую материальную точку М, соединенную с горизонтальной осью вращения (осью привеса) z гибкой нерастяжимой невесомой нит (или абсолютно жестким невесомым стержнем), движущуюся в вертикальной плоскости. Расстояние материальной точки от оси вращения называется длиной математического маятника.
Пусть вес математического маятника равен Р, а длина — l. Рассматривая математический маятник как частный случай физического маятника, применим для вывода дифференциального уравнения движения математического маятника уравнение (111.219), в котором
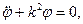
Таким образом, движение математического маятника описывается дифференциальным уравнением, аналогичным уравнению движения физического маятника.
Для круговой частоты колебаний /с и периода колебаний Т математического маятника получим
Приведенной длиной физического маятника называется длина синхронного с ним математического маятника, т. е. математического маятника, имеющего тот же период колебаний, что и физический маятник.
Приравняв периоды колебаний математического и физического маятников или выражения (111.224) и (111.222), получим
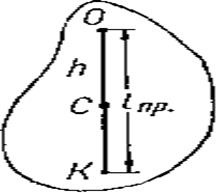
На расстоянии приведенной длины /пр от точки привеса О (рис. 116) находится точка К, которая называется центром колебаний (качаний) физического маятника.
Центр колебаний физического маятника имеет следующие свойства:
1. Центр тяжести маятника расположен между центром колебаний и точкой привеса, следовательно lпр>h.
2. Если заставить маятник колебаться вокруг оси, проходящей через центр колебаний и параллельной его оси привеса, то точка привеса О будет новым центром колебаний такого физического маятника.
Это свойство взаимозаменяемости точки привеса и центра колебаний физического маятника (теорема Гюйгенса) используется в оборотном маятнике Картера, применяемом для определения ускорения силы тяжести в различных точках земной поверхности.
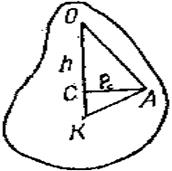
Рассмотрим графический способ нахождения центра колебаний физического маятника, основанный на том, что радиус инерции маятника относительно центральной оси ρc есть средняя пропорциональная между длиной h маятника и расстоянием КС его центра инерции от центра колебаний (рис. 116).
а на основании формулы (111.80)
Как видно из рис. 116, lпр-h=KC=h1. Поэтому 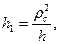
Для нахождения центра колебаний отложим из точки С перпендикулярно к отрезку h отрезок рс (рис. 117) и конец его А соединим с точкой привеса О. Затем под прямым углом к ОА проведем прямую до пересечения с продолжением ОС в искомой точке К — центре колебаний физического маятника. Заметим при этом, что ρc можно отложить как вправо, так и влево от точки С.
Дата добавления: 2015-08-08 ; просмотров: 2159 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Колебания материальной точки в теоретической механике
Содержание:
Колебания материальной точки:
К исследованию колебаний одной материальной точки могут быть сведены многие технические задачи
В качестве примера интегрирования дифференциальных уравнений движения рассмотрим колебания материальной точки. Еще совсем недавно изучение колебаний не входило в программу курсов теоретической механики высших учебных заведений. Но необходимость создания новых методов расчета всевозможных машин и различных сооружений, обладающих большой прочностью при небольшом весе, а также необходимость увеличения скоростей и производигельности машин стимулировали быстрое развитие раздела динамики, называемого теорией колебаний. Раздел, посвященный колебаниям, включен теперь во все программы по теоретической механике.
C основами явлений колебаний удобно ознакомиться сперва на примере, колебания одной материальной точки. Изучение вибраций одной материальной точки интересно также и потому, что к вибрации точки могут быть непосредственно приведены многие практически важные задачи.
Пусть точка M массы m притягивается к точке О силой F, пропорциональной (рис. 162) расстоянию ОМ, а начальная скорость точки M направлена по прямой OM или равна нулю. В таком случае точка M будет двигаться по прямолинейной траектории, вдоль которой мы направим ось х. Начало координат возьмем в точке О (в равновесном положении). Сила F как бы стремится вернуть точку M в равновесное положение О, за что ее называют восстанавливающей силой. Примером такой силы могут служить сила упругости стержня, совершающего малые колебания, или равнодействующая сил веса G и натяжения T нити при малых колебаниях маятника и т. и. Чем больше координата х, тем больше величина этой силы. Вместе с тем сила (точнее говоря, ее проекция на ось Ох) по знаку всегда противоположна знаку координаты х. В самом деле, если точка M находится справа от x начала координат О, то координата х положительна, а сила направлена в отрицательную сторону, и наоборот, если координата х отрицательна, то восстанавливающая сила направлена в положительную сторону. Обозначив коэффициент пропорциональности между силой и расстоянием через с (причем с > 0), выразим восстанавливающую силу формулой
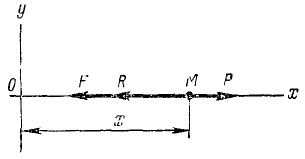
Рис. 162
Пусть на точку M во время ее движения действует сила сопротивления R, пропорциональная скорости точки и направленная против скорости. Таким образом, если точка M движется вправо (х > 0), то сила сопротивления направлена влево (R 0. Обозначив коэффициент пропорциональности через а (причем а > 0), мы определим силу сопротивления (выражаясь точнее, ее проекцию на ось Ох) формулой
Кроме того, пусть на точку M действует возмущающая сила Р, т. е. некоторая дополнительная сила, вызывающая изменение движения, обусловленного основной силой F. Возмущающая сила направлена по прямолинейной траектории точки M и, периодически изменяя свою величину и знак, раскачивает точку M то в ту, то в другую сторону. Мы ограничимся рассмотрением простейшего случая и предположим, что сила P изменяется с течением времени по закону синуса:
P = H sin pt. (133)
Очевидно, что сила P изменяется в пределах от +Н до —Н. Пример такой силы приведен в задаче № 110.
Напишем дифференциальное уравнение движения точки M:
Разделив обе части уравнения на т, введем обозначения
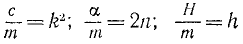
и перенесем члены, содержащие х или его производные, влево:
х + 2nx + k 2 x =h sin pt. (135)
Мы имеем неоднородное линейное дифференциальное уравнение с постоянными коэффициентами. Общее решение такого уравнения складывается из: 1) общего решения соответствующего однородного уравнения, т. е. уравнения (135) без правой части, и какого-либо частного решения неоднородного уравнения (135).
Для интегрирования уравнения
х + 2nx + k 2 x = 0
составим характеристическое уравнение
z 2 + 2nz + k 2 = 0.
Если n 2 sin (pt— δ)
и подставим в (135) написанное выражение х и его производных:
— Bp 2 sin (pt — δ) + 2nBp cos (pt — δ) + k 2 B sin (pt — δ) = h sin pt.
Преобразуем правую часть этого равенства:
h sin pt = h sin (pt — δ +δ) = h sin (pt — δ) cos ∂ + h cos (pt — δ) sin δ.
Перенеся все члены влево и собирая члены, содержащие sin(pt— δ) и cos (pt — δ), получим
[В (k 2 —p 2 )-h cos δ] sin (pt — δ) + (2Bnp-hsin δ) cos (pt — δ) = O.
Это равенство обращается в тождество, если
В (k 2 — р 2 ) = h cos δ; 2Bnp = h sin δ,
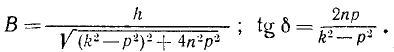
Складывая общее решение (136) однородного уравнения с найденным частным решением неоднородного уравнения, получим общее решение неоднородного уравнения (135) в таком виде:
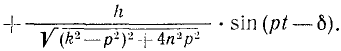
Прежде чем исследовать сложное колебательное движение точки под действием сил F, R и P, выражаемое уравнением (138), рассмотрим более простые движения, которые точка совершала’ бы под действием одной силы F или же под действием силы F и какой-либо- одной из двух остальных R или Р.
Точка, движущаяся по прямой, совершает под действием восстанавливающей силы гармоническое колебание
Свободные колебания без сопротивления
Предположим, что на материальную точку M (см. рис. 162 на стр. 274) действует только восстанавливающая сила (131), сила же сопротивления (132) и возмущающая сила (133) равны нулю. Пусть начальная скорость точки M направлена по прямой MO или равна нулю. В таком случае точка M будет двигаться по прямой OM (по оси Ох), дифференциальное и кинематическое уравнения ее движения мы получим, положив в (135) и в (138) n и h равными нулю. В самом деле, если сила сопротивления R=O, то, следовательно, α = 0, потому что R=— ах и х переменная величина. Если же a = 0, то равно нулю и n, которое согласно (134) равно 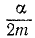
В таком случае уравнение (135) принимает вид
Этому уравнению придадим более удобный вид, для чего выразим, постоянные интегрирования C1 и C2 через две другие постоянные величины А и β, однозначно связанные с C1 и C2 соотношениями
x = A sin (kt+ β). (140)
Это уравнение является одним из важнейших уравнений в теории колебаний и описывает наиболее простое колебательное движение, называемое гармоническим. Еще в древности было известно, что если некоторая точка M’ (рис. 163) равномерно движется по окружности радиуса О’М’ — А со скоростью kA, то проекция M этой точки на какую-либо ось Ох, лежащую в плоскости окружности, совершает гармонические колебания. Мы воспользуемся рис. 163, чтобы нагляднее ознакомить читателя с параметрами гармонического колебания.
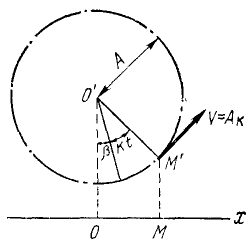
Рис. 163
Если точка M’ опишет полную окружность, то точка M’ совершит одно полное колебание.
Время одного полного колебания точки M (или, что то же, время,в течение которого точка M’ описывает одну полную окружность) называют периодом -τ0 колебаний.
Угловая скорость k, с которой поворачивается радиус-вектор 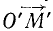
Период и угловая частота связаны простым соотношением, которое становится очевидным, если учесть, что τ0—это время, в течение которого 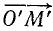
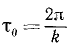
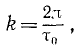
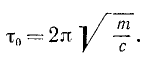
Период имеет размерность времени
Частота имеет размерность угловой скорости
Из (141) видно, что круговая частота k равна числу полных колебаний, совершаемых в 2π сек. Частота ν колебаний пропорциональна круговой (циклической, угловой) частоте k и равна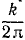
Максимальное отклонение А точки M от среднего (равновесного) положения О в ту или в другую сторону (или, что то же, радиус круговой траектории точки М’) называют амплитудой. Амплитуду измеряют в единицах длины:
Аргумент синуса (kt + β) называют фазой колебания, a β—начальной фазой. Физический смысл фазы колебания выявляется при сравнении двух колебаний с одинаковыми частотами, но с разными начальными фазами. Колебание с фазой (kt+ β) опережает колебание с фазой kt, а колебание с фазой (kt — β) отстает от него (разумеется, при положительном β).
Напомним, что А и β являются постоянными интеграции, а следовательно, их определяют по начальным данным. Пусть в начальное мгновение t = 0, x=x0 и x=x0. Продифференцировав (140) по времени, получим х = Ak cos (kt + β), и подставляя начальные значения:
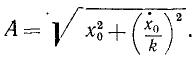
Из тех же равенств можно определить и начальную фазу 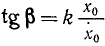
Задача №1
Груз весом 2 T подвешен на тросе (рис. 164). При равномерном спуске груза со скоростью υ = 5м/сек произошла неожиданная задержка верхнего конца троса вследствие защемления троса в обойме блока. Пренебрегая весом троса, определить его наибольшее натяжение при последующих колебаниях груза, если коэффициент жесткости троса с = 4 T/см.
Решение. Примем следующие единицы измерений: длина—в см, время — в сек, сила—в Т. Рассмотрим движение груза. На груз действуют две силы: вертикально вниз вес груза 2T, вертикально вверх — натяжение троса. Груз спускался равномерно, следовательно, до защемления натяжение троса равнялось весу груза. В этом равновесном положении его застала авария. После защемления троса груз не остановился мгновенно. В это мгновение он имел скорость 5 м/сек и продолжал опускаться. Но по мере опускания груза сила натяжения троса возрастала от своего начального значения 2T. Ускорение груза направлено по силе и пропорционально ей. Поэтому опускание груза было замедленным и в некоторое мгновение скорость груза, перейдя через нуль, стала направленной вверх, в направлении силы и ускорения. Движение вверх было ускоренным, но по мере того как груз поднимался, растяжение троса, а следовательно, и его натяжение уменьшались, а потому уменьшалось ускорение груза, скорость же продолжала увеличиваться до момента прохождения через равновесное положение. После этого груз, набрав скорость, продолжал подниматься, ио замедленно, так как натяжение троса стало меньше силы веса и равнодействующая приложенных к грузу сил была направлена вниз. Затем скорость стала равной нулю, груз начал падать вниз, натяжение троса возрастало и движение повторялось снова неопределенное количество раз.
Начало О системы отсчета выберем обязательно в равновесном положении груза, относительно которого происходят колебания, направив ось Ox вертикально вниз (рис. 164). В начальное мгновение (в момент защемления троса) было: x0= 0; x0= 500 см/сек. Квадрат круговой частоты определим по (134). После подстановки в формулу 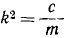
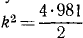
Таким образом, при равновесном положении груза натяжение троса равно 2T; когда же груз опустился на одну амплитуду, то трос растянулся еще на 11,28 см, а при жесткости троса в 4 T/см натяжение его увеличилось еще на 45,12 Т.
Натуральный логарифм отношения двух последующих амплитуд затухающих колебаний называют логарифмическим декрементом
Свободные колебания с сопротивлением
Движение под действием восстанавливающей силы и силы сопротивления будем называть свободными колебаниями. Мы только что убедились, что свободные колебания без сопротивления являются гармоническими и, раз возникнув, они повторялись бы до тех пор, пока их не прекратила бы или не изменила бы какая-нибудь внешняя сила. Пусть возмущающая сила отсутствует (P = 0, H = 0, h = 0), а на точку действуют силы F=-cx и R =—ах. Дифференциальное уравнение (135) движения точки M принимает вид
х + 2nx 4- k 2 x = 0, (144)
а его интеграл получим, положив в (138) h=0:
или, если воспользуемся соотношениями (140),
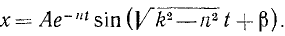
Постоянные А и β определяют по начальным данным.
Наиболее существенное отличие уравнения (145) от уравнения (140), иначе говоря, наиболее существенное изменение в свободном колебании точки М, внесенное наличием силы сопротивления, заключается в множителе e -nt , который с течением времени непрерывно уменьшается, вследствие чего амплитуда Ae -nt колебаний с сопротивлением убывает по экспоненциальному закону, асимптотически приближаясь к нулю. Такое колебание называют затухающим.
Переходя к определению периода затухающих колебаний, обратим внимание на то, что вообще периодом периодического движения называют промежуток времени между двумя последовательными прохождениями точки (или системы) через одно и то же положение водном и том же направлении. В случае затухающих колебаний только равновесное положение удовлетворяет такому определению периода, через всякое же другое положение точка M (или любая система, совершающая затухающие колебания) проходит через неравные промежутки времени (см. рис. 165). Поэтому под периодом затухающих колебаний понимают промежуток времени τ1 между двумя последовательными прохождениями точки M (или системы) через положение равновесия в одинаковом направлении. В таком же смысле колебания, описываемые уравнением (145), могут быть названы изохронными. Период затухающих колебаний можно определить но формуле
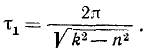
Проф. И. М. Бабаков в учебнике «Теория колебаний» рекомендует для практических расчетов более удобную формулу:
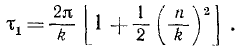
Сравнивая (141) и (146), мы видим, что сопротивление увеличивает период свободных колебаний, но незначительно.
Гораздо больше оно влияет на убывание амплитуд. Так, например, при n = 0,05 k сопротивления увеличивают период на 0,125%, а амплитуда за время одного полного колебания уменьшается более чем на 25%. На рис. 165 изображен график затухающих колебаний для случая n = 0,05 k, позаимствованный из «Лекций» проф. Е. Л. Николаи.
Отношение абсолютных значений двух последовательных амплитудных отклонений точки от равновесного положения называют коэффициентом затухания:
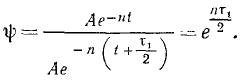
Для характеристики быстроты убывания амплитуды удобнее пользоваться натуральным логарифмом коэффициента затухания, называемым логарифмическим декрементом колебаний:
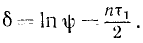
На рис. 165 пунктиром изображены кривые, уравнения которых x= Ае -n и х = —Ae -nt . График затухающих колебаний расположен между этими двумя кривыми и поочередно их касается.
Задача №2
Маятник, масса которого равна 1 кг и период качания в безвоздушной среде τ0=l сек, заставили качаться вереде, сопротивляющейся но закону R =—2х н. Определить: 1) период затухающих колебаний маятника и 2) уменьшение амплитуды в течение трех периодов.
Решение. Определим параметры колебаний.
Круговая частота. Период τ0=l сек= 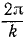
Коэффициент α=2; m=1; 2n=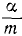
Период затухающих колебаний 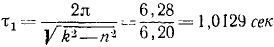
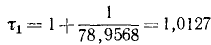
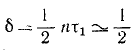
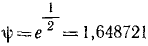
Отношение каждого максимального отклонения к последующему (через полпериода) равно коэффициенту затухания, следовательно, если амплитуду при первом размахе принять за 1, то следующие уменьшаются в отношении 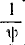
Под действием восстанавливающей и возмущающей сил точка совершает сложное колебание, являющееся результатом наложения трех гармонических колебаний: свободного, сопровождающего свободного и вынужденного
Вынужденные колебания без сопротивления
Пусть на точку М, движущуюся по оси Ох, действуют две силы — восстанавливающая F=— CX и возмущающая P =H sin pt, направленные также по оси Ох. Величина pt может быть названа фазой силы, постоянную р назовем круговой частотой возмущающей силы, а период этих изменений обозначим через τ. Действие сопротивления мы пока не учитываем, поэтому, положив в уравнении (135) n = 0, получим следующее дифференциальное уравнение вынужденных колебаний без сопротивления:
x+ k 2 x = h sin pt. (148)
Чтобы найти решение этого уравнения, надо в (138) положить равным нулю не только n, но и δ, так как согласно (137) δ = 0 при n = 0. Имеем
Определим постоянные. Если в начальное мгновение х = x0 и x = χ0, то
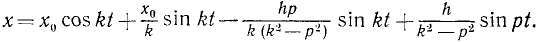
Первые два слагаемых описывают свободные колебания с частотой k. Воспользовавшись соотношениями (140″), эти два слагаемых можно представить в виде x1 = A sin (kt + β). Если в начальное мгновение х = х= 0, то эти колебания во все время действия возмущающей силы не возникают. Третье слагаемое
— гармоническое колебание, происходящее с частотой k свободных колебаний, но с амплитудой, зависящей от возмущающей силы. Это колебание всегда, при любых начальных условиях, сопровождает вынужденные колебания и его называют свободным сопровождающим колебанием. Четвертое слагаемое
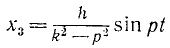
описывает вынужденные колебания. Таким образом, колебания точки являются результатом линейного наложения трех гармонических колебаний: 1) свободных, 2) сопровождающих свободных и 3) вынужденных (рис. 166):
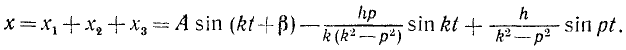
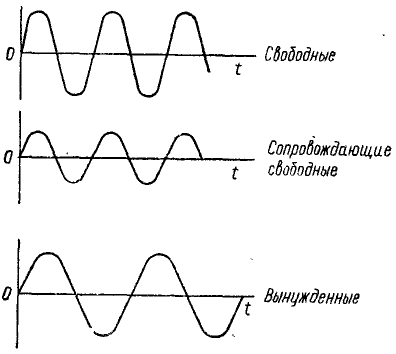
Рис. 166
На схеме (рис. 166) приведены только частоты этих колебаний, но разумеется, не изображены амплитуды и начальные фазы.
Вынужденные колебания происходят с частотой р, равной частоте возмущающей силы. Они не зависят от начальных данных.
Как видно из (143), для изменения амплитуды свободных колебаний достаточно изменить начальное отклонение или начальную скорость. Напротив, для изменения амплитуды вынужденных колебаний надо изменить возмущающую силу, что обычно бывает сопряжено с необходимостью преобразования конструкции.
Если частота р вынужденных колебаний меньше частоты k собственных (случай «малой» частоты), то амплитуда вынужденных колебаний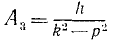
с фазой pt возмущающей силы. По если р > k (случай «большой» частоты), то выражение, написанное для А3, становится отрицательным, однако амплитуда не может быть отрицательной. Это кажущееся несоответствие объясняется тем, что при р > k фаза вынужденных колебаний противоположна фазе возмущающей силы и уравнение вынужденных колебаний имеет вид
Резонанс
Если частоты собственных и вынужденных колебаний близки между собой, то амплитуды получаются очень большими. Напомним, что при интегрировании уравнения (135) мы положили p≠k. Если р= k, то дифференциальное уравнение (148) имеет вид
x-k 2 x = h sin kt (148′)
Будем искать частное решение вида
Определив х =— 2Bk sin kt— Btk 2 cos kt и подставив его вместе с х в дифференциальное уравнение, получим
— 2Bk sin kt = h sin kt,
Находим общее решение дифференциального уравнения движения:
Дифференцируем по времени:
Если в начальное мгновение x=x0 и x=x0, то
и общее решение принимает вид
или, полагая 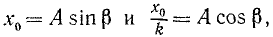
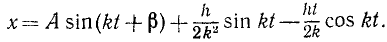
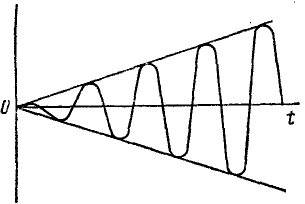
Следовательно, и при равенстве частот движение точки состоит из трех колебательных движений, однако вынужденные колебания представлены непериодическим членом, в коэффициент которого входит множителем время. C течением времени это третье слагаемое, называемое вековым членом, безгранично растет по абсолютной величине. Размах вынужденных колебаний непрерывно растет по линейному закону. Это явление называется резонансом. График вынужденных колебаний при резонансе представлен на рис. 167.
Задача №3
Груз M подвешен в точке В к пружине AB (рис. 168), верхний конец А которой прикреплен к поступательно движущейся кулисе. Кривошип кулисного механизма имеет длину а = 0,02 м и вращается с угловой скоростью 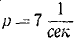
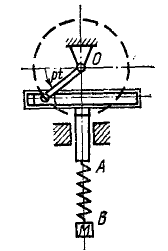
Рис. 168
Решение. Составим дифференциальное уравнение движения груза М. Начало координат выберем в точке, с которой центр тяжести груза совладал в момент начала движения (при t = 0), когда верхний конец А пружины, совершающей гармонические колебания вместе с кулисой, занимал свое среднее положение. При сделанном нами выборе начала отсчета (в равновесном положении груза) вес G = 3,6 н уравновешивался статическим натяжением пружины с λcr = 36 ∙ 0,1. Наличие этих двух взаимно уравновешенных сил эквивалентно их отсутствию, а потому мы можем их отбросить и в дальнейшем рассматривать движение центра тяжести груза лишь под действием натяжения пружины, обусловленного только ее динамической деформацией, т. е. только деформацией пружины при колебании груза около равновесного положения.
При t ≠ 0 положение центра тяжести груза определяется координатой х, получающейся от суммирования двух перемещений: динамической деформации пружины и перемещения a sin pt верхнего конца А пружины. Следовательно, динамическая деформация пружины равна разности перемещений ее нижнего конца В и верхнего конца А, т. е. равна х—α sin pt . Дифференциальное уравнение движения центра груза имеет вид
mx = — с (х—a sin pt).
Деля обе части уравнения на m и вводя обозначения 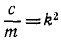
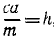
x + k 2 x = h sin pt,
где
Подставляя в (149′), находим вынужденные колебания груза.
Ответ. 0,04 sin 7t.
Задача №4
Статический прогиб рессор товарного вагона равен 5 см. Определить критическую скорость вагона, при которой начнется «галопирование» вагона, если на стыках рельсов вагон испытывает толчки, вызывающие вынужденные колебания на рессорах: длина рельсов равна 12 м.
Решение. Жесткость рессор 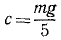
Если поезд идет со скоростью υ см/сек, то вагон получает толчки на стыках через каждые 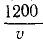
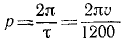
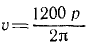
Чтобы выразить скорость в км/ч, умножим выраженную в см/ceκ скорость на 0,036.
Если к точке приложены восстанавливающая и возмущающая сила и сила сопротивления, то свободные колебания затухают и остаются только вынужденные
Влияние сопротивления на вынужденные колебания
Если на точку, кроме восстанавливающей и возмущающей сил, действует также и сила R сопротивления, то движение точки описывается дифференциальным уравнением (135) и его решением (138).
Первый член правой части (138) с возрастанием t стремится к нулю, и соответствующие ему колебания точки с течением времени затухают, поэтому ими можно пренебречь. Остаются только вынужденные колебания (рис. 169):
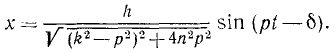
Они происходят с частотой возмущающей силы, сопротивление не влияет на период вынужденных колебаний. Амплитуда не зависит от начальных условий и времени и не изменяется с течением времени.
Предположим, что возмущающая сила сохраняет свое максимальное значение Н. При равновесии под действием такой силы и восстанавливающей силы F =— сх точка M получила бы так называемое статическое отклонение
Из этого соотношения найдем максимальное ускорение точки M под действием возмущающей силы: h=k 2 xст и, подставляя это значение h в выражение (150), выразим амплитуду вынужденных колебаний равенством
Отношение частоты вынужденных колебаний к частоте собственных колебаний
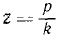
носит название коэффициента расстройки и отношение величины n, измеряемой в ceκ -1 , к частоте собственных колебаний называют безразмерным коэффициентом вязкости:
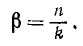
Введя эти обозначения в предыдущее равенство и разделив обе части его на xст, получим:
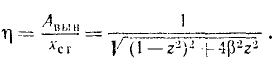
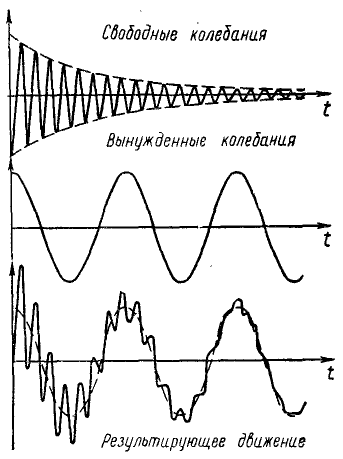
Рис. 169
Величина η—коэффициент динамичности — позволяет охарактеризовать динамический эффект, вызываемый возмущающей силой.
Коэффициент динамичности η зависит от двух величин (z и β).
Задавшись каким-либо значением β, и откладывая по оси абсцисс различные значения z, а по оси ординат—соответствующие значения коэффициента динамичности η, получим, так называемые, резонансные кривые. На рис. 170 изображены резонансные кривые для значений безразмерного коэффициента вязкости: 0,25, 0,15. и 0,10. Пунктиром нанесена уходящая в бесконечность при 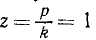
Как показывает график (рис. 170) в областях, достаточно далеких от резонанса, амплитуды вынужденных колебаний с сопротивлением почти не зависят от безразмерного коэффициента вязкости. В этих областях при вычислении амплитуд вынужденных колебаний можно не учитывать сопротивлений и пользоваться более простой формулой
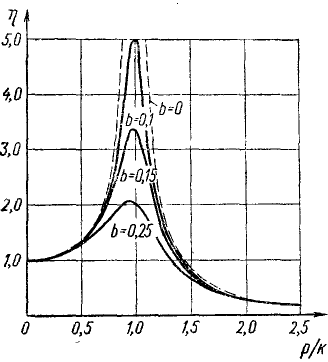
Рис. 170
При резонансе (р = k) амплитуда вынужденных колебаний при наличии сопротивлений остается конечной, но наибольшее значение амплитуда имеет, если 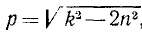
В вынужденных колебаниях с сопротивлением всегда бывает сдвиг фазы колебания по отношению к фазе .возмущающей силы. Величина этого сдвига определяется формулой (137).
Заметим, что все сказанное здесь относительно малых колебаний материальной точки полностью соответствует малым колебаниям материальной системы с одной степенью свободы.
| Рекомендую подробно изучить предмет: |
|
| Ещё лекции с примерами решения и объяснением: |
- Количество движения
- Момент количества движения
- Мощность и работа силы
- Потенциальная энергия
- Естественный и векторный способы определения движения точки
- Координатный способ определения движения точки
- Касательное и нормальное ускорения точки
- Основные законы динамики
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Уравнение колебаний маятника
Рис.1
Исследуем выражение (2) в зависимости от разности фаз (φ2 — φ1):
1) φ2 — φ1 = ±2mπ (m = 0, 1, 2, . ), тогда A=A1+A2, т. е. амплитуда результирующего колебания А будет равна сумме амплитуд складываемых колебаний;
2) φ2 — φ1 = ±(2m+1)π (m = 0, 1, 2, . ), тогда A=|A1–A2|, т. е. амплитуда результирующего колебания будет равна разности амплитуд складываемых колебаний.
Для практики представляет особый интерес случай, когда два складываемых гармонических колебания одинакового направления мало отличаются по частоте. После сложения этих колебаний получаются колебания с периодически изменяющейся амплитудой. Периодические изменения амплитуды колебания, которые возникают при сложении двух гармонических колебаний с близкими частотами, называются биениями.
Пусть амплитуды складываемых колебаний равны А, а частоты равны ω и ω+Δω, причем Δω
23 Колебания физического маятника.
Физический маятник — осциллятор, представляющий собой твёрдое тело, совершающее колебания в поле каких-либо сил относительно точки, не являющейся центром масс этого тела, или неподвижной оси, перпендикулярной направлению действия сил и не проходящей через центр масс этого тела.
Определения
— угол отклонения маятника от равновесия;
— начальный угол отклонения маятника;
— масса маятника;
— расстояние от точки подвеса до центра тяжести маятника;
— радиус инерции относительно оси, проходящей через центр тяжести.
— ускорение свободного падения.
Момент инерции относительно оси, проходящей через точку подвеса:

[править] Дифференциальное уравнение движения физического маятника
Основная статья: Приведённая длина
Пренебрегая сопротивлением среды, дифференциальное уравнение колебаний физического маятника в поле силы тяжести записывается следующим образом:
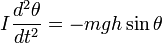
Полагая 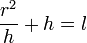
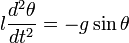
Последнее уравнение аналогично уравнению колебаний математического маятника длиной 

[править] Центр качания физического маятника
Центр качания — точка, в которой надо сосредоточить всю массу физического маятника, чтобы его период колебаний не изменился.
Поместим на луче, проходящем от точки подвеса через центр тяжести точку на расстоянии 
Действительно, если всю массу сосредоточить в центре качания, то центр качания будет совпадать с центром масс. Тогда момент инерции относительно оси подвеса будет равен 
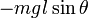
[править] Теорема Гюйгенса
[править] Формулировка
Если физический маятник подвесить за центр качания, то его период колебаний не изменится, а прежняя точка подвеса сделается новым центром качания.
[править] Доказательство
Вычислим приведенную длину для нового маятника:
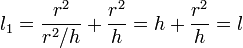
Совпадение приведённых длин для двух случаев и доказывает утверждение, сделанное в теореме.
[править] Период колебаний физического маятника
Для того, чтобы найти период колебаний физического маятника, необходимо решить уравнение качания. Для этого умножим левую часть этого уравнения на 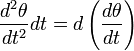
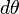
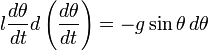
Интегрируя это уравнение, получаем.
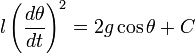
где 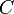
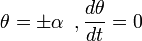
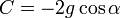
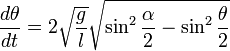
Отделяем переменные и интегрируем это уравнение:
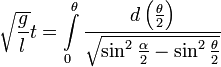
Удобно сделать замену переменной, полагая 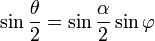
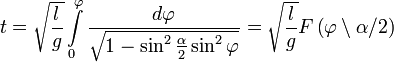
Здесь 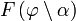
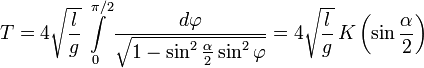
Здесь 
[править] Период малых колебаний физического маятника
Если амплитуда колебаний 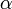
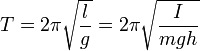
24 Колебания математического маятника
Математи́ческий ма́ятник — осциллятор, представляющий собой механическую систему, состоящую из материальной точки, находящейся на невесомой нерастяжимой нити или на невесомом стержне в однородном поле сил тяготения. Период малых собственных колебаний математического маятника длины l неподвижно подвешенного в однородном поле тяжести с ускорением свободного падения g равен
и не зависит [1] от амплитуды и массы маятника.
Плоский математический маятник со стержнем — система с одной степенью свободы. Если же стержень заменить на растяжимую нить, то это система с двумя степенями свободы со связью. Пример школьной задачи, в которой важен переход от одной к двум степеням свободы.
При малых колебаниях физический маятник колеблется так же, как математический с приведённой длиной.
Уравнение колебаний маятника
Колебания математического маятника описываются обыкновенным дифференциальным уравнением вида
где ω ― положительная константа, определяемая исключительно из параметров маятника. Неизвестная функция x(t) ― это угол отклонения маятника в момент t от нижнего положения равновесия, выраженный в радианах; 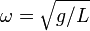
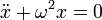
[править] Решения уравнения движения
[править] Гармонические колебания
Маятник, совершающий малые колебания, движется по синусоиде. Поскольку уравнение движения является обыкновенным ДУ второго порядка, для определения закона движения маятника необходимо задать два начальных условия — координату и скорость, из которых определяются две независимых константы:
где A — амплитуда колебаний маятника, θ0 — начальная фаза колебаний, ω — циклическая частота, которая определяется из уравнения движения. Движение, совершаемое маятником, называется гармоническими колебаниями
[править] Нелинейный маятник
Для маятника, совершающего колебания с большой амплитудой, закон движения более сложен:
где 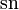

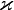
Параметр 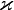
где 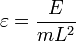
Период колебаний нелинейного маятника
где K — эллиптический интеграл первого рода.
[править] Движение по сепаратрисе
Движение маятника по сепаратрисе является непериодическим. В бесконечно далёкий момент времени он начинает падать из крайнего верхнего положения в какую-то сторону с нулевой скоростью, постепенно набирает её, и останавливается, возвратившись в исходное положение.
25 Затухающие колебания. Зависимость амплитуды от времени.
Затухающие колебания — колебания, энергия которых уменьшается с течением времени. Бесконечно длящийся процесс вида 
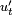
Пускай имеется система, состоящая из пружины (подчиняющейся закону Гука), один конец которой жёстко закреплён, а на другом находится тело массой m. Колебания совершаются в среде, где сила сопротивления пропорциональна скорости с коэффициентом c (см. вязкое трение).
Тогда второй закон Ньютона для рассматриваемой системы запишется так:
где Fc — сила сопротивления, Fy — сила упругости
или в дифференциальной форме
где k — коэффициент упругости в законе Гука, c — коэффициент сопротивления, устанавливающий соотношение между скоростью движения грузика и возникающей при этом силой сопротивления.
Для упрощения вводятся следующие обозначения:
Величину ω называют собственной частотой системы, ζ — коэффициентом затухания.
Тогда дифференциальное уравнение принимает вид
Сделав замену x = e λt , получают характеристическое уравнение
Корни которого вычисляются по следующей формуле
[править] Решения
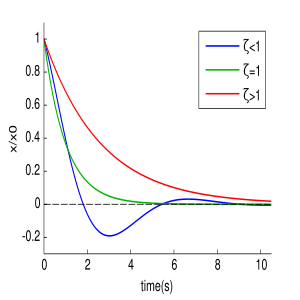
Зависимость графиков колебаний от значения ζ.
В зависимости от величины коэффициента затухания решение разделяется на три возможных варианта.
Если 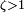
В этом случае колебания с самого начала экспоненциально затухают.
- Граница апериодичности
Если 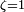
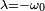
В данном случае может иметь место вре́менный рост, но потом — экспоненциальное затухание.
Если 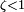
Тогда решением исходного дифференциального уравнения является
Где 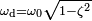
Константы c1 и c2 в каждом из случаев определяются из начальных условий:
26 Вынужденные колебания. Понятие резонанса.
Вынужденные колебания — колебания, происходящие под воздействием внешних сил, меняющихся во времени.
Автоколебания отличаются от вынужденных колебаний тем, что последние вызваны периодическим внешним воздействием и происходят с частотой этого воздействия, в то время как возникновение автоколебаний и их частота определяются внутренними свойствами самой автоколебательной системы.
Наиболее простой и содержательный пример вынужденных колебаний можно получить из рассмотрения гармонического осциллятора и вынуждающей силы, которая изменяется по закону: 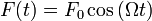
http://www.evkova.org/kolebaniya-materialnoj-tochki-v-teoreticheskoj-mehanike
http://poisk-ru.ru/s49779t9.html
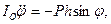
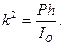
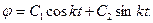
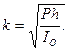
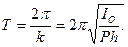
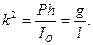
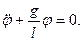
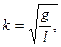
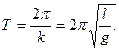
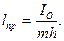
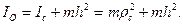
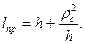
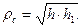
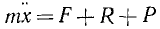
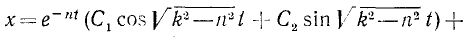
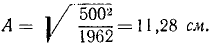
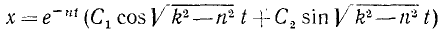
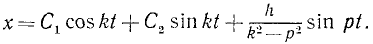
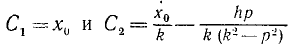
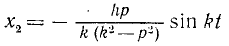
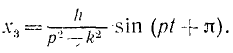
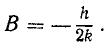
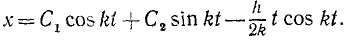
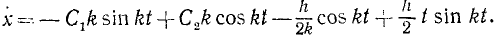
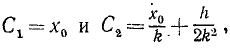
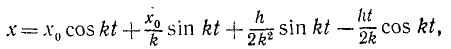
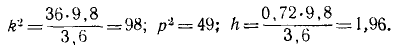
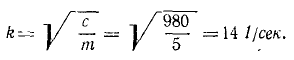
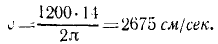
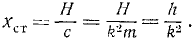
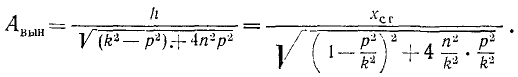
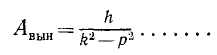
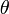 — угол отклонения маятника от равновесия;
— угол отклонения маятника от равновесия; — масса маятника;
— масса маятника;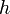 — расстояние от точки подвеса до центра тяжести маятника;
— расстояние от точки подвеса до центра тяжести маятника; — радиус инерции относительно оси, проходящей через центр тяжести.
— радиус инерции относительно оси, проходящей через центр тяжести.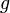 — ускорение свободного падения.
— ускорение свободного падения.