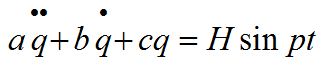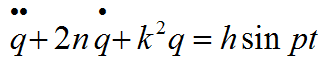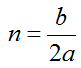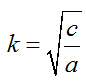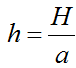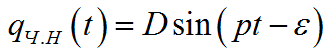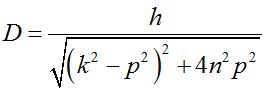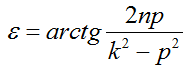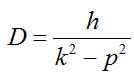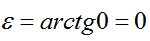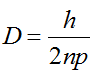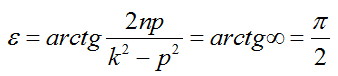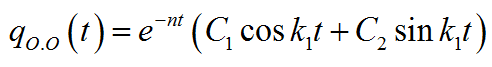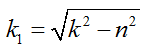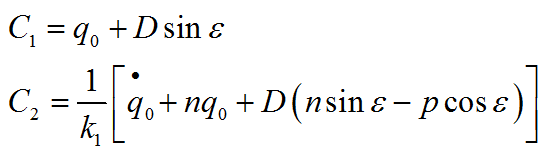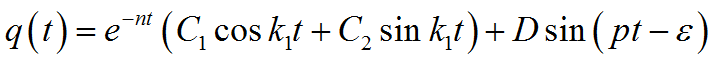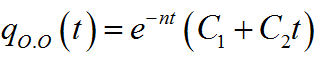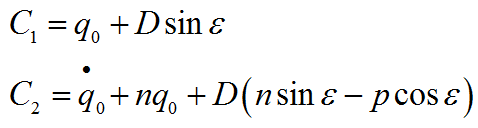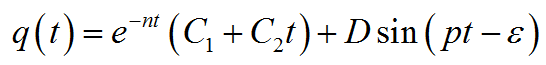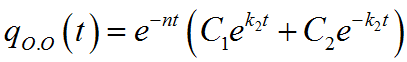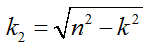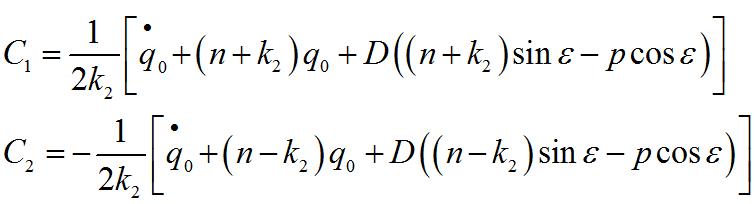Уравнение малых колебаний в общем виде

Теоретическая механика. Малые колебания

Дифференциальное уравнение малых вынужденных колебаний с вязким сопротивлением в общем виде выглядит так

Приводим его к каноническому виду.

— частота собственных колебаний

— амплитуда вынуждающего воздействия.

Решение данного дифференциального уравнения выглядит как сумма общего и частного решений.

Частное решение всегда выглядит одинаково. В общем виде:

— амплитуда вынужденных колебаний

— сдвиг фаз – отставание по фазе установившихся вынужденных колебаний от вынуждающей причины.

В зависимости от условий задачи возможны частные случаи.

При отсутствии вязкого сопротивления (n=0)

Если при этом собственная частота колебаний совпадает с частотой возбуждающей причины (k=p), возникает явление резонанса и амплитуда D стремится к бесконечности.

При наличии сопротивления, но равенстве n=k, резонанс невозможен.

Если по условию задачи возбуждение отсутствует (рассматриваются свободные колебания), т.е. h=0, p=0, то частное решение ДУ нулевое.

Теперь займемся общим решением.

Общее решение дифференциального уравнения зависит от соотношения k и n.

При k>n имеем случай малого сопротивления.

Для этого случая решение однородного уравнения запишем в виде:

Постоянные интегрирования определяем из начальных условий

Тогда окончательное решение дифференциального уравнения

При k=n имеем случай критического сопротивления.

Для этого случая решение однородного уравнения запишем в виде:

Постоянные интегрирования определяем из начальных условий

Тогда окончательное решение дифференциального уравнения

При k

Постоянные интегрирования определяем из начальных условий

Тогда окончательное решение дифференциального уравнения

Малые колебания

Автор: Пользователь скрыл имя, 14 Ноября 2011 в 22:51, реферат

Краткое описание

Очень распространенный тип движения механических систем это так называемые малые колебания, которые система совершает вблизи своего положения равновесия.
Рассмотрим наиболее простой случай, когда система обладает всего одной степенью
свободы – эта система называется линейный осциллятор.

Файлы: 1 файл

малые колебания.docx

1.Свободные одномерные колебания.

Очень распространенный тип движения механических систем это так называемые малые колебания, которые система совершает вблизи своего положения равновесия.

Рассмотрим наиболее простой случай, когда система обладает всего одной степенью

свободы – эта система называется линейный осциллятор.

Функция Лагранжа в случае

Устойчивому положению равновесия соответствует положение, в котором потенциальная энергия имеет мнимое значение, т.е. , где и обобщенные силы , которые вызывают колебания в потенциальной яме при отклонении тела от положения равновесия.

Предположим, что эти отклонения малы и при малых отклонениях системы от положения равновесия разложит потенциальную энергию U(q) в ряд по степеням малости отклонений в окружности положения равновесия.

Произведем масштабное преобразование координат, т.е.будем отсчитывать потенциальную энергию от , U()=0

Учтем, что как точка минимума U(q) (на самом дне потенциальной силы).

Обозначим и назовем коэффициентом квазиупругой силы.

Обозначим –отклонение тела от положения равновесия, которое называется смещением.

Перейдя в случае однородных колебаний к декартовой координате, т.е.

Обозначая,a(x)=m получим функцию Лагранжа для одномерных малых колебаний. Подставим в уравнение Лагранжа:

дифференциальное уравнение движения.

Вводя – собственная частота

Решение. Дифференциальное уравнение – второго порядка или его можно привести к виду – уравнение смещения для линейного гармоничного асцилятора, где Α — амплитуда, ωt+α-фаза, α- начальная фаза.

Как его получить? Исходим из уравнения движения

По общему правилу решения ищем решение в виде

Общее решение ДУ-2 запишем в виде суперпозиции двух уравнений

т.к. x- это смещение, то это действительная величина, а критерием действительности величины является в комплексном анализе то, что

Тогда представим const и также в комплексной форме где a-модуль комплексного числа, мнимая часть числа , но тогда сравнивая их тогда

Учитывая, получим мы пришли к выражению (1) где A=2a

Выражение (1) можно представить в комплексной форме такой вид записи в комплексной форме намного удобнее тригонометрической, поскольку с экспонентами легче работать. Часто пишут просто , и выполняя преобразования и дойдя до ответа необходимо просто в конечном ответе учесть что надо взять действительную часть числа и получим решение. В такой записи — комплексная амплитуда,a- амплитуда,- начальная фаза

МАЛЫЕ КОЛЕБАНИЯ СИСТЕМ СО МНОГИМИ СТЕПЕНЯМИ СВОБОДЫ (МНОГОМЕРНЫЕ МАЛЫЕ КОЛЕБАНИЯ)

Функция Лагранжа системы со многими степенями свободы

Рассмотрим малые колебания вблизи положения равновесия, т.е. вблизи некоторой точки с координатами Это та точка, в которой потенциальная энергия имеет min т.е. экстремум.

1.Исследование потенциальной энергии.

Вводя аналогично одномерным колебаниям малые отклонения тела от положения равновесия , которые бу дем называть смещением, разложим потенциальную энергию в ряд по степеням малости в окрестности положения равновесия

Отсчитывая потенциальную энергию от можно положить U(

Введем обозначение — коэффициенты квазиупругой силы

Причем коэффициент и на дне потенциальной ямы двойные производные должны быть «+» т.е. из коэффициентов можно составить матрицу- . С имметрическая матрица, которая в евклидовом пространстве представляет собой положительно определённую квадрируемую форму , где критерием положительной определенности та кой квадрируемой формы является то, что определители все более высокого ранга должны быть положительны.

3) >0 т.е. и сама потенциальная энергия (1) так же является положительно определенной квадрируемой формой координат

2. Исследование кинетической энергии

Обозначим это значение коэффициентов рассчитанные в точке равновесия, тогда кинетическая энергия т.е. и кинетическая энергия также является положительно определенной квадрируемой формой скоростей, где

3.Функция и уравнение Лагранжа

Объединяя первое и второе, составим функцию Лагранжа малых многомерных колебаний (3) и подставим (3) в уравнение Лагранжа, которых будет n-малое штук.

Собираем производные в уравнение Лагранжа, получим (4) , но i=1,…,n.

Т.е. уравнение движений для малых колебаний представляют собой систему линейных однородных дифференциальных уравнений с постоянными коэффициентами, и по общему правилу ищем решение в виде (5)

Подставляем (5) в (4) , т.к. ( i=1,…,n)

Для этой системы уравнений существует тривиальное решение, когда все коэффициенты =0 (j=1,…,n), но оно нас не интересует . Но для того, чтобы эта система имела отличие от нуля решения, необходимо чтобы обращался в нуль ее определитель, т.е. Выражение (7) называется характеристическим уравнением

Это уравнение служит для определения частот , это уравнение n-ой степени относительно . Решив его, мы находим n-малое частот (выбирая из них , т. е. те частоты , которые имеют реальный физический смысл). Именно такие частоты называются собственными частотами систем.

После нахождения частот, их необходимо подставить в уравнение (6) и найти значение коэффициента матриц а. Тогда решение уравнения это уравнение движения для первой из степеней свободы при многомерных колебаниях примет вид Каждая координата зависит от всех частот.

Если все корни характеристического уравнения (7) различны, т.е. то коэффициенты про порциональны минорам определителя характеристического уравнения где комплексная постоянная, тогда общее решение , где — уравнение для однородного осциллятора. Сравнив с предыдущим пунктом, где мы начинаем понимать, что под мы можем понимать уравнение движения относительно отдельной степени свободы.

Т.е. изменения каждой из координат системы со временем представляет собой положение n-простых периодических колебаний , …, с произвольными амплитудами и фазами, частотами, но вполне определёнными частотами.

5)Колебания линейного осциллятора при наличии вынужденной силы.

Т.к. колебания малые, то и внешнее поле будем полагать достаточно малым, иначе оно может вызвать большие смещения. Пусть, как и раньше — это собственная потенциальная энергия — потенциальная энергия квазиупругой силы. Под действием внешнего поля система будет обладать также потенциальной энергией , где x — смещение

Разложим в ряд по степеням малости смещение (x) в окрестности положения равновесия , но эта функция только времени и по третьему свойству функции Лагранжа ее можно исключить, как полную производную над некоторой другой функции времени
. Подставим в функцию Лагранжа для свободной колебательной системы

Подставим в уравнение Лагранжа , — дифференциальное уравнение движения

Будем рассматривать частный случай, когда внешняя вынужденная сила имеет периодический характер где – частота начальная фаза

Частный случай: (2), но решение неоднородного дифференциального уравнения , где общее решение однородного уравнения, соответствующее уравнению движения свободного гармонического осциллятора

Частный интеграл не однородного уравнения будем искать в виде ,подставим

уравнение движения линейного осциллятора под действием периодической вынужденной силы. Его движение представляет собой наложение двух колебаний с частотами и

Здесь возможны три случая:

1)Если колебания происходят в противофазе

2)Если колебания происходят в фазе

3)Если и это резкое увеличение амплитуды вынужденных колебаний, при совпадений собственной частоты колебательной системы и частоты внешней вынужденной силы.

Гармонические колебания

О чем эта статья:

9 класс, 11 класс, ЕГЭ/ОГЭ

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Механические колебания

Механические колебания — это физические процессы, которые точно или приблизительно повторяются через одинаковые интервалы времени.

Колебания делятся на два вида: свободные и вынужденные.

Свободные колебания

Это колебания, которые происходят под действием внутренних сил в колебательной системе.

Они всегда затухающие, потому что весь запас энергии, сообщенный в начале, в конце уходит на совершение работы по преодолению сил трения и сопротивления среды (в этом случае механическая энергия переходит во внутреннюю). Из-за этого свободные колебания почти не имеют практического применения.

Вынужденные колебания

А вот вынужденные колебания восполняют запас энергии внешним воздействием. Если это происходит каждый период, то колебания вообще затухать не будут.

Вынужденные колебания — это колебания, которые происходят под действием внешней периодически меняющейся силы.

Частота, с которой эта сила воздействует, равна частоте, с которой система будет колебаться.

Например, качели. Если вас кто-то будет на них качать, каждый раз давая толчок, когда вы приходите в одну и ту же точку — такое колебание будет считаться вынужденным.

Это колебание все еще будет считаться вынужденным, если вас будут раскачивать из положения равновесия. Просто в данном случае амплитуда (о которой речь пойдет чуть ниже) будет увеличиваться с каждым колебанием.

Автоколебания

Иногда вынужденному колебанию не нужно внешнего воздействия, чтобы случиться. Бывают такие системы, в которых это внешние воздействие возникает само из-за способности регулировать поступление энергии от постоянного источника.

У автоколебательной системы есть три важных составляющих:

• сама колебательная система
• источник энергии
• устройство обратной связи, обеспечивающей связь между источником и системой

Часы с кукушкой — пример автоколебательной системы. Гиря на ниточке (цепочке) стремится вращать зубчатое колесо (храповик). При колебаниях маятника анкер цепляет за зубец, и вращение приостанавливается.

Но в результате маятник получает толчок, компенсирующий потери энергии из-за трения. Потенциальная энергия гири, которая постепенно опускается, расходуется на поддержание незатухающих колебаний.

Характеристики колебаний

Чтобы перейти к гармоническим колебаниям, нам нужно описать величины, которые помогут нам эти колебания охарактеризовать. Любое колебательное движение можно описать величинами: период, частота, амплитуда, фаза колебаний.

Период — это время одного полного колебания. Измеряется в секундах и обозначается буквой T.

Формула периода колебаний

T = t/N

N — количество колебаний [—]

Также есть величина, обратная периоду — частота. Она показывает, сколько колебаний совершает система в единицу времени.

Формула частоты

ν = N/t = 1/T

N — количество колебаний [—]

Амплитуда — это максимальное отклонение от положения равновесия. Измеряется в метрах и обозначается либо буквой A, либо x max .

Она используется в уравнении гармонических колебаний:

Гармонические колебания

Простейший вид колебательного процесса — простые гармонические колебания, которые описывают уравнением:

Уравнение гармонических колебаний

x — координата в момент времени t [м]

t — момент времени [с]

(2πνt) в этом уравнении — это фаза. Ее обозначают греческой буквой φ

Фаза колебаний

t — момент времени [с]

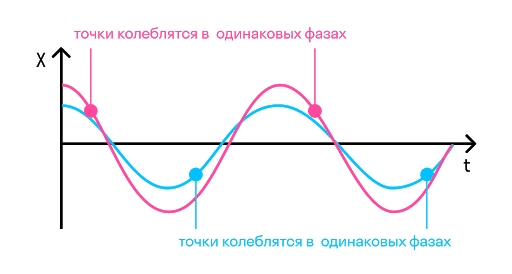
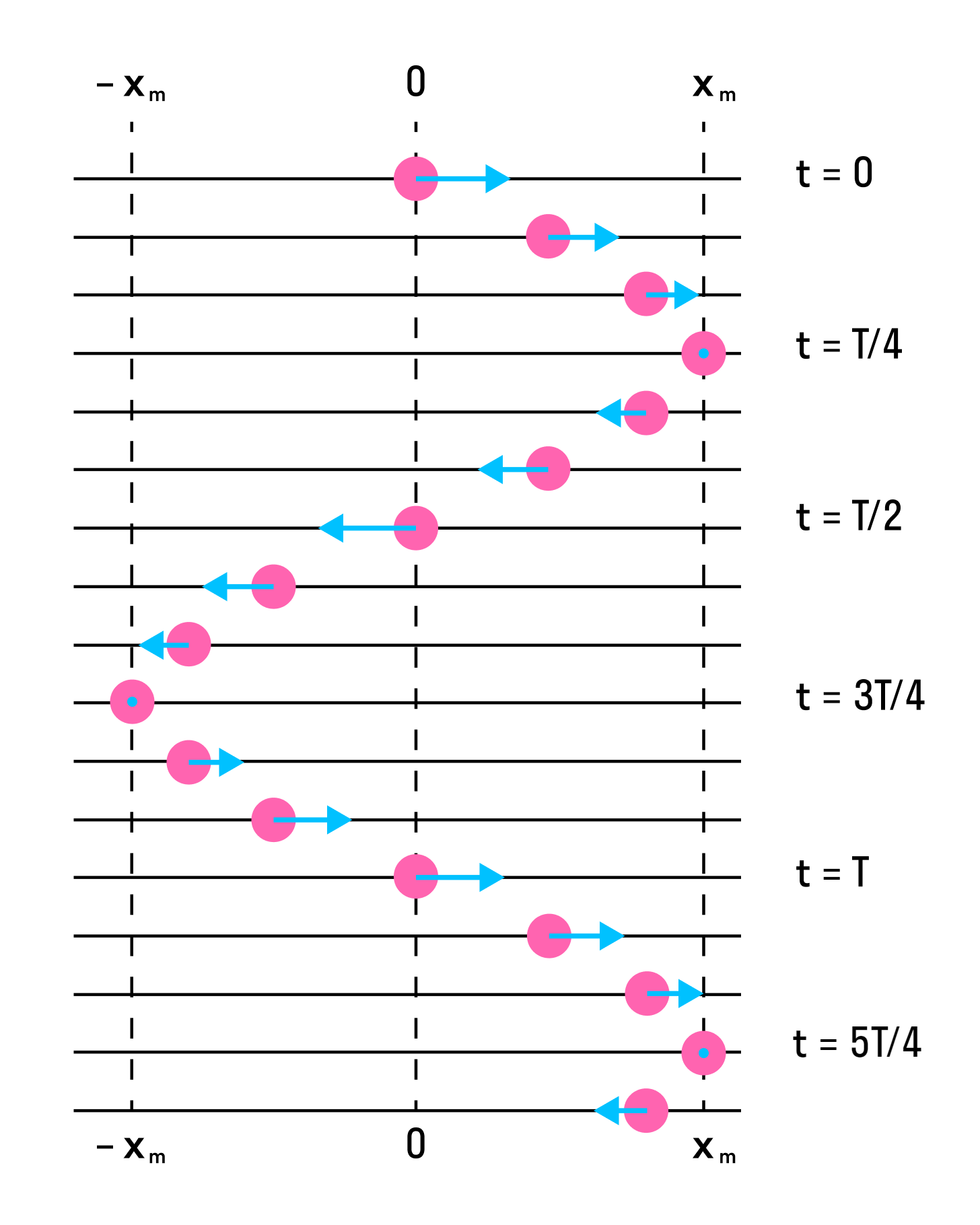
Фаза колебаний — это физическая величина, которая показывает отклонение точки от положения равновесия. Посмотрите на рисунок, на нем изображены одинаковые фазы:

Например, в тех же самых часах с кукушкой маятник совершает колебания. Он качается слева направо и приходит в самую правую точку. В той же фазе он будет находиться, когда придет в ту же точку, идя справа налево. Если мы возьмем точку на сантиметр левее самой правой, то идя в нее не слева направо, а справа налево, мы получим уже другую фазу.

На рисунке ниже показаны положения тела через одинаковые промежутки времени при гармонических колебаниях. Такую картину можно получить при освещении колеблющегося тела короткими периодическими вспышками света (стробоскопическое освещение). Стрелки изображают векторы скорости тела в различные моменты времени.

Если изменить период, начальную фазу или амплитуду колебания, графики тоже изменятся.

На рисунке ниже во всех трех случаях для синих кривых начальная фаза равна нулю, а в последнем (с) — красная кривая имеет меньшую начальную фазу.

В первом случае (а) красная кривая описывает колебание, у которого амплитуда больше колебания, описанного синей линией.

Во втором случае (b) красная кривая отличается от синей только значением периода — у красной период в два раза меньше.

Математический маятник

Математический маятник — отличный пример гармонических колебаний. Если мы подвесим шарик на нити, то это еще не будет математическим маятником — пока он только физический.

Математическим этот маятник станет, если размеры шарика много меньше длины нити (тогда этими размерами можно пренебречь и рассматривать шарик как материальную точку), растяжение нити очень мало, а масса нити во много раз меньше массы шарика.

Математическим маятником называется система, которая состоит из материальной точки массой m и невесомой нерастяжимой нити длиной l, на которой материальная точка подвешена, и которая находится в поле силы тяжести (или других сил).

Период малых колебаний математического маятника в поле силы тяжести Земли определяется по формуле:

Формула периода колебания математического маятника

l — длина нити [м]

g — ускорение свободного падения [м/с 2 ]

На планете Земля g = 9,8 м/с 2

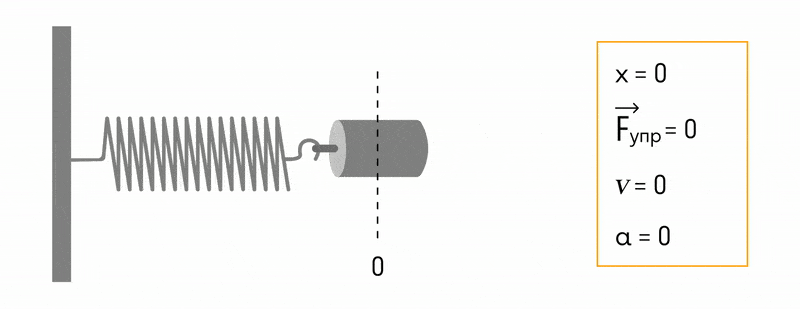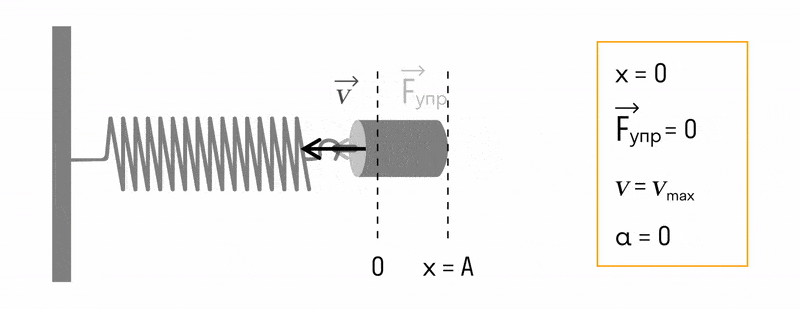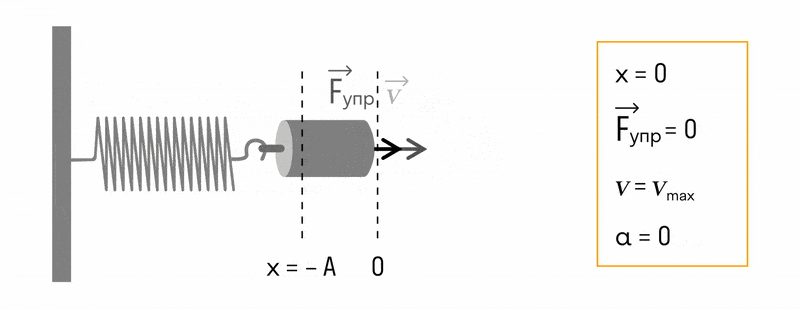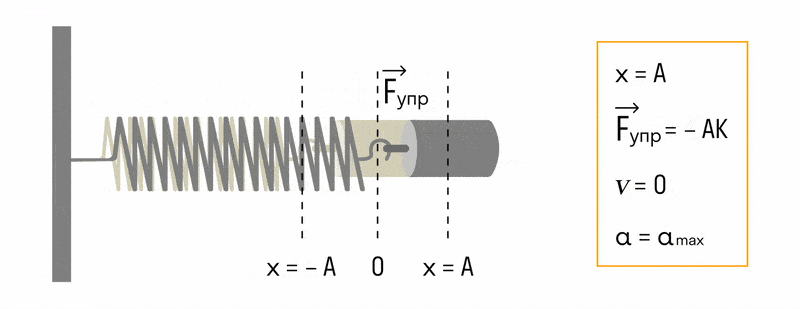
Пружинный маятник

Пружинный маятник — это груз, прикрепленный к пружине, массой которой можно пренебречь.

В пружинном маятнике колебания совершаются под действием силы упругости.
Пока пружина не деформирована, сила упругости на тело не действует.

Формула периода колебания пружинного маятника

m — масса маятника [кг]

k — жесткость пружины [Н/м]

Закон сохранения энергии для гармонических колебаний

Физика — такая клевая наука, в которой ничего не исчезает бесследно и не появляется из ниоткуда. Эту особенность описывает закон сохранения энергии.

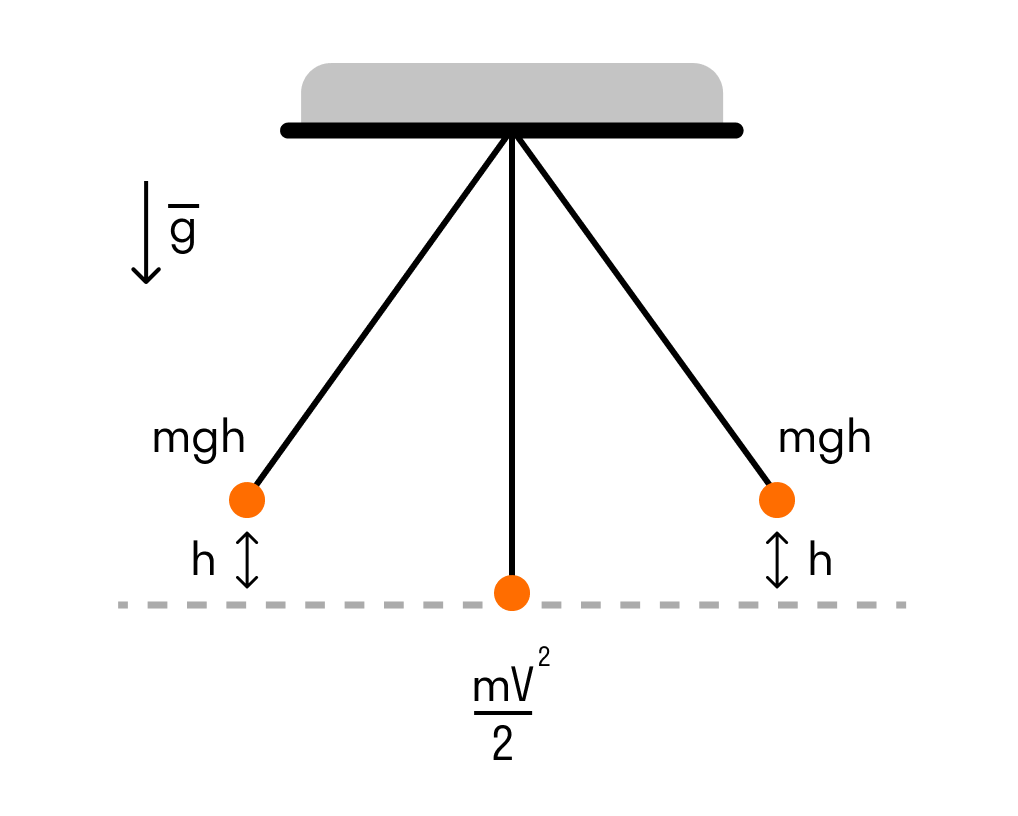
Рассмотрим его на примере математического маятника.

• Когда маятник отклоняют на высоту h, его потенциальная энергия максимальна.
• Когда маятник опускается, потенциальная энергия переходит в кинетическую. Причем в нижней точке, где потенциальная энергия равна нулю, кинетическая энергия максимальна и равна потенциальной энергии в верхней точке. Скорость груза в этой точке максимальна.

Онлайн-курсы физики в Skysmart не менее увлекательны, чем наши статьи!