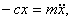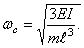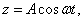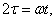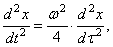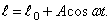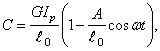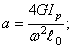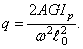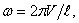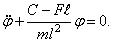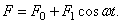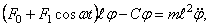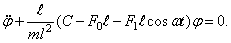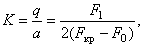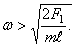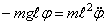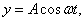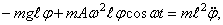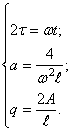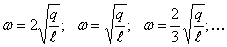Раздел 4. Параметрические колебания
4.1. Основное уравнение (уравнение Матье)
В ряде случаев параметры механической системы — ее жесткость или масса — не остаются неизменными, а являются некоторыми заданными функциями времени, чаще периодическими. Если нарушить состояние равновесия такой системы, то будут происходить своеобразные колебания: с одной стороны, их нельзя назвать свободными, так как система испытывает определенное внешнее воздействие в виде изменения жесткости, а с другой — они не являются вынужденными, так как внешнее воздействие не проявляется в виде заданной возмущающей силы. Эти колебания называются параметрическими и в зависимости от свойств системы и характера изменения ее параметров могут иметь ограниченные или возрастающие амплитуды, причем во втором случае возможно наступление параметрического резонанса.
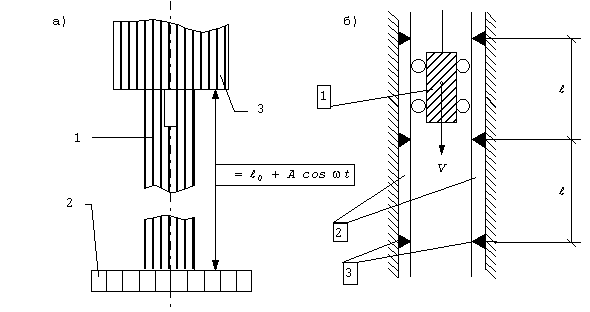
Рассмотрим простейшую систему (рис.56). Сосредоточенная масса 1 закреплена на конце невесомого стержня 2. Свобода перемещений стержня дополнительно ограничена втулкой 3, удаленной от нижнего конца стержня на расстояние 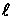
Составим уравнение свободных колебаний груза, считая, что они происходят в плоскости чертежа. Если в текущий момент времени t перемещение груза составляет x , то восстанавливающая сила упругости стержня равна — cx , а уравнение движения груза имеет вид
где c — коэффициент жесткости системы.
Втулка 3 при ее достаточной длине обеспечивает практически полное защемление нижней части стержня, и тогда 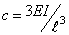
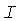
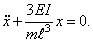
Если расстояние 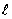
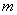
Теперь предположим, что втулка 3 скользит вдоль стержня 2 по заданному закону
т.е. совершает около среднего положения 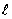
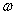
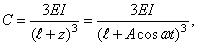
и дифференциальное уравнение (148) становится уравнением с переменными коэффициентами:
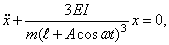
что характерно для системы с параметрическим возбуждением колебаний.
Существует много других механических систем, подверженных параметрическому возбуждению. Ряд примеров убеждает, что в большинстве практически важных случаев дифференциальное уравнение параметрических колебаний можно привести к стандартной форме:
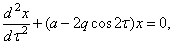
где a и q — некоторые постоянные.
Возвращаясь к механической системе, показанной на рис.56, положим, что амплитуда колебаний втулки A весьма мала по сравнению с длиной 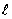
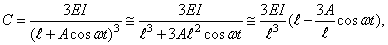
и дифференциальное уравнение (150) принимает вид
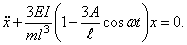
Перейдем к безразмерному времени 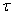
и дифференциальное уравнение (153) приобретает стандартную форму (151), причем
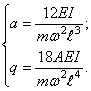
Основное уравнение параметрических колебаний (151) называется уравнением Матье. Решения этого уравнения носят колебательный характер и главным образом зависят от конкретных значений параметров a и q . В одних случаях данной комбинации a и q соответствуют колебания, ограниченные по амплитуде, а в других — колебания с возрастающими амплитудами. Основную практическую важность представляет именно тенденция колебательного процесса: если амплитуды остаются ограниченными, то система устойчива; в противном случае имеет место параметрический резонанс, и система неустойчива.
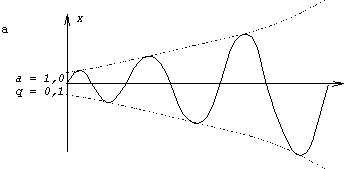
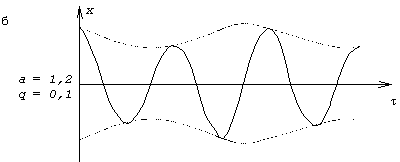
Результаты решения уравнения Матье для двух различных комбинаций a и q показаны на рис.57 (эти решения получены при помощи электронного аналогового устройства). Хотя в обоих случаях параметр q системы одинаков ( q = 0,1), колебания имеют совершенно разный характер из-за различия между значениями параметра a ( a = 1; a = 1,2). В первом случае амплитуды возрастают, т.е. система неустойчива, а во втором случае остаются ограниченными, т.е. система устойчива.
Для практических целей наибольшее значение имеют границы между областями устойчивых и неустойчивых решений. Этот вопрос хорошо исследован, причем окончательные результаты представляются в виде диаграммы, построенной в плоскости параметров a и q , которая называется диаграммой Айнса-Стретта.
Каждой данной системе, характеризуемой параметрами a и q , соответствует точка с координатами a , q на диаграмме Айнса-Стретта (изображающая точка). Если изображающая точка находится в пределах заштрихованных полей диаграммы, то система устойчива; неустойчивым системам соответствуют изображающие точки, расположенные на белых полях.
На рис.58 показана часть диаграммы Айнса-Стретта, относящаяся к малым значениям параметра q . В качестве примера на диаграмме указаны точки 1 и 2, соответствующие параметрам a 1 = 1; q 1 = 0,1; a 2 = 1,2; q 2 = 0,1 (решения уравнения Матье для этих случаев даны на рис.57).
Точка 1 находится в белой зоне (неустойчивость), и колебания происходят с возрастающими амплитудами (рис.57,а). Точка 2 находится в пределах заштрихованной зоны; ей отвечает движение с ограниченной амплитудой (рис.57,б).
В плоскости параметров a , q области устойчивости чередуются с областями неустойчивости, причем наиболее широкая, а потому и наиболее важная область неустойчивости содержит точку a = 1, q = 0. Диаграмма Айнса-Стретта полностью освобождает от выполнения каких-либо операций по решению уравнения Матье. Достаточно составить это уравнение, т.е. найти значения параметров системы a и q , после чего диаграмма дает ответ на вопрос об устойчивости или неустойчивости системы.
При возрастании частоты возбуждения параметры a и q уменьшаются. Так как отношение этих параметров остается постоянным, то последовательные состояния системы определяются изображающими точками на луче 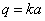
4.2. Случаи периодического изменения жесткости
В качестве примера рассмотрим систему, упругой частью которой является зубчатый (шлицевой) вал 1 (рис.59,а). На нижнем конце вала находится диск 2. С валом соединена зубчатая (шлицевая) массивная втулка 3, которая может скользить вдоль оси вала и совершать гармонические колебания в вертикальном направлении. В этой системе возможно возбуждение не только изгибных, но и крутильных колебаний. Пусть свободная длина вала в текущий момент времени t составляет
Коэффициент жесткости вала на кручение:
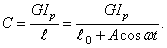
Если амплитуда колебаний А значительно меньше среднего значения длины 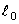
что по структуре совпадает с (152), следовательно, крутильные колебания рассматриваемой системы также описываются уравнением Матье (151), причем
При некоторых условиях, определяемых диаграммой Айнса-Стретта, рассматриваемая система может оказаться в состоянии параметрического резонанса.
Другим примером параметрического возбуждения колебаний при периодическом изменении жесткости является система, изображенная на рис.59,б. Шахтная клеть 1 равномерно движется по вертикальным направляющим 2, которые закреплены на шпалах 3. В этой системе поперечная жесткость, определяющая восстанавливающую упругую силу при поперечных колебаниях клети, есть величина переменная: если клеть находится на уровне очередной пары шпал, то эта жесткость достигает максимума, если же клеть расположена против середины свободного пролета направляющих, то жесткость минимальна. Частота изменения жесткости зависит от расстояния между шпалами и от скорости движения клети:
а отсюда следует, что существует ряд «запретных» диапазонов скорости V , соответствующих условиям параметрического резонанса. Эти соображения полностью подтверждены экспериментальными исследованиями.
4.3. Случаи периодического изменения параметрических нагрузок
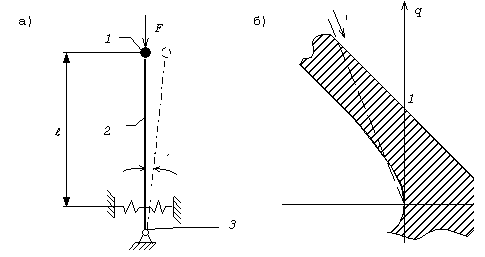
Простейший пример рассматриваемого типа представлен на рис.60,а.
Масса 1 закреплена на верхнем конце вертикального абсолютно жесткого стержня 2; внизу стержень имеет опору, упруго сопротивляющуюся повороту опорного сечения («упругий шарнир»). На верхний конец стержня действует вертикальная сила F . Такая система представляет собой результат упрощенной схематизации реального стержня, обладающего распределенными массой и упругостью.
Сила F является параметрической нагрузкой, и если она постоянна во времени, ее критическое значение можно найти при помощи формулы Эйлера.
Пусть 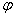
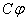
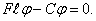
Очевидно, что 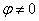
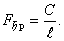
Этой формулой определяется критическое значение статически действующей силы F ( например веса груза 1).
Это же значение можно найти, рассматривая свободные колебания груза 1. В отличие от уравнения статики (156) уравнение моментов относительно шарнира 3 содержит инерционное слагаемое:
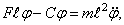
При 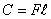
Рассмотрим случай, когда сила F изменяется во времени, следуя гармоническому закону:
При этом уравнение колебаний стержня (158) принимает вид
Это уравнение приводится к стандартной форме — уравнению Матье (151), если положить
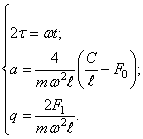
При возрастании частоты 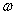
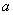
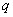
где 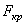
При данном значении 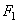
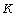
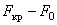
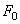
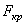
Потеря устойчивости возможна при сколь угодно малых значениях сжимающей статической составляющей 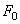
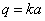
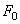
С другой стороны, диаграмма Айнса-Стретта позволяет установить, что устойчивость системы возможна при 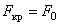
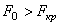
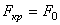
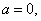
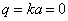
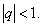
При 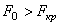
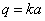
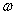
4.4. Маятник с колеблющейся точкой подвеса
Рассмотрим маятник (рис.61,а). Если точка подвеса неподвижна, то единственной силой, создающей момент относительно точки подвеса, является вес груза 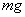
Уравнение малых колебаний маятника имеет вид
Если же точка подвеса колеблется вдоль оси y по закону
то при составлении уравнения моментов нужно учесть переносную силу инерции 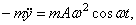
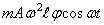
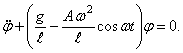
Уравнение (160) можно привести к стандартному виду — уравнению Матье.
Для этого положим:
Теперь из диаграммы Айнса-Стретта видно, что параметр а не зависит от амплитуды колебаний точки подвеса и сколь бы малой ни была амплитуда 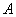
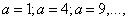
Рассмотрим вопрос об устойчивости верхнего положения маятника (рис.61,б). При неподвижной опоре это положение, конечно, неустойчиво; однако вибрации основания могут придать ему устойчивость. Для получения уравнения движения в данном случае достаточно изменить знак перед членом, содержащим ускорение 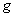
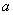
Из рис .61,в видно, что верхнее положение маятника может быть устойчивым. При небольших амплитудах колебаний 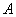
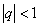
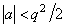
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Выполнение контрольных, курсовых, дипломных работ Качество и своевременность
Анализ процессов в параметрическом колебательном контуре на основе уравнения Матье.
В предыдущем параграфе мы рассмотрели энергетический способ исследования параметрических систем. Данный L метод, позволил вывести формулы, определяющие значение коэффициента модуляции, при котором в колебательной системе возможно либо усиление колебаний, либо стационарный режим, либо нарастающие колебания.
В данном параграфе рассматривается другой часто применяемый способ исследования колебаний в параметрических системах, описываемых дифференциальными уравнениями второго порядка:
Анализ процесса в рассматриваемом параметрическом контуре, основан на сведение уравнений, описывающих колебания в контуре, к уравнению Матье:
Пусть параметрическая емкость колебательного контура изменяется по закону
Запишем с помощью МКТ дифференциальное уравнение параметрических колебаний:
Мы получили интегро-дифференциальное уравнение. Для того чтобы получить дифференциальное уравнение, сделаем замену переменных:
, которое позволяет перейти к дифференциальному уравнению 2го порядка ( введем новые обозначения ), следующего вида:
избавиться от производной 1го порядка, сделаем следующую замену переменных
Подставляя найденные q(t), и в полученное дифференциальное уравнение, получаем
Введем безразмерное время:
У нас уравнение с периодическими коэффициентами, причем коэффициенты a и b – положительные величины. Кроме того, из вида a и b видно, что b
Решение уравнения Матье, строится с помощью теоремы Флоке, которая гласит, что для уравнений типа Хилла (у которого коэффициенты являются периодическими функциями), решение является почти периодическими функциями:
Отсюда следует, что функция удовлетворяет теореме Флоке, если φ(r) периодическая функция.
Этому уравнению удовлетворяет и функция y2=e -μrφ(r).
Возникли периодические функции, которые называются функциями Матье:
φ( )=φ( ,a,b).
μ= μ(a,b) – некий коэффициент, зависящий от параметров a и b.
Причем a и b – вещественные положительные числа.
а) если , то — описывает стационарные решения.
б) если — вещественная величина, то решения расходятся, и следовательно они описывают нарастающие колебания.
в) если — мнимая величина, то решения будут сходящимися, а колебания затухающими.
Рассмотрим однородное уравнение Матье.
, в котором устремим коэффициент b к нулю. Тогда уравнение примет вид:
решение, которого выражается через тригонометрические функции
Вид решения для у(τ) не изменится (т.е. будет выполняться теорема Флоке), только если . Т.е. только в этом случае сдвиг фазы на приведёт к тому, что значение функции не изменится.
Отыскание в общем случае проблема. Поэтому строятся диаграммы значений параметров а и в, при которых решение для у(τ) будет иметь различный характер поведения.
Т.к. функции у1(τ) и у2(τ) удовлетворяют теореме Флоке, тогда решение уравнения Матье будет представляться как комбинация этих двух функций:
В связи с тем, что , тогда коэффициент в мал, и можно предположить, что у(τ) не сильно отличается от тригонометрической функции (случай когда в=0):
с учетом того, что тогда
Если частоты модуляции и накачки, а также параметр модуляции такие, что решения попадают в нижнюю часть зоны, то энергия отклика превышает начальную энергию. Т.е. у нас зона усиления регенеративного типа. Если попадает в верхнюю часть зоны, то эта зона где вносимая энергия превышает энергию потерь, и у нас возникнет режим автоколебаний. Для этих значений можно определить критическое значение параметра – mкр. Области помеченные звездочками, не имеют практического значения, т.к. там происходит еще большее затухание, т.т де регенерация.
Выводы. Т.о. в целях получения параметрического усиления или возбуждения колебаний, следует использовать такое соотношение параметров а и в(т.е. ω0, λ и m), при котором решение соответствует областям неустойчивости. Если при этом коэффициент модуляции m меньше mкрn в системе можно осуществить регенеративное усиление. Если же m больше mкрn в системе происходит параметрическое возбуждение нарастающих колебаний, которые в дальнейшем ограничиваются какими-либо нелинейными элементами, которые неизбежно существуют в цепях.
ПАРАМЕТРИ́ЧЕСКИЙ РЕЗОНА́НС
В книжной версии
Том 25. Москва, 2014, стр. 304-305
Скопировать библиографическую ссылку:
ПАРАМЕТРИ́ЧЕСКИЙ РЕЗОНА́НС, явление раскачки колебаний при периодич. изменении параметров тех элементов колебательной системы, в которых сосредоточена энергия колебаний (реактивные или энергоёмкие параметры). П. р. возможен в колебательных системах разл. физич. природы. Напр., в электрич. колебательном контуре реактивными параметрами являются ёмкость $C$ и индуктивность $L$ , в которых запасены электрич. энергия $W_э=q^2/2C$ и магнитная энергия $W_м=LI^2/2$ (здесь $q$ – электрич. заряд на обкладках конденсатора, $I$ – ток в катушке индуктивности). Собств. колебания в контуре без потерь с постоянными $C$ и $L$ происходят с частотой $ω_0=1/\sqrt
http://all-about-car.ru/volna/parametr13.htm
http://bigenc.ru/physics/text/2707243