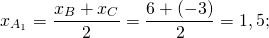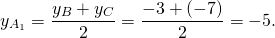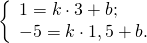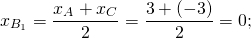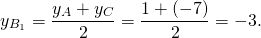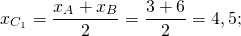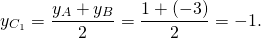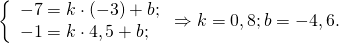Уравнение медианы am и ее длину

Уравнение медианы треугольника

Как составить уравнение медианы треугольника по координатам его вершин?

Медиана соединяет вершину треугольника с серединой противолежащей стороны. Следовательно, при решении задачи составления уравнения медианы нужно:

1. Найти координаты середины отрезка по координатам его концов.
2. Составить уравнение прямой, проходящей через две точки: найденную середину отрезка и противолежащую вершину.

Дано: ΔABC, A(3;1), B(6;-3), C(-3;-7).

Найти уравнения медиан треугольника.

Обозначим середины сторон BC, AC, AB через A₁, B₁, C₁.

Уравнение медианы AA₁ будем искать в виде y=kx+b.

Найдём уравнение прямой, проходящей через точки A(3;1) и A₁(1,5;-5). Составляем и решаем систему уравнений:

Отсюда k= 4; b= -11.

Уравнение медианы AA₁: y=4x-11.

2) Аналогично, координаты точки B₁ — середины отрезка AC

Можно в уравнение y=kx+b подставить координаты точек B(6;-3) и B₁(0;-3) и найти k и b. Но так как ординаты обеих точек равны, уравнение медианы BB₁ можно найти ещё быстрее: y= -3.

3) Координаты точки C₁ — середины отрезка BC:

Отсюда уравнение медианы CC₁ : y=0,8x-4,6.

Задача 20272 2. Даны вершины треугольника ABC: A(-1;.

Условие

2. Даны вершины треугольника ABC: A(-1; 7), B(11; 2), C(17; 10).

а) уравнение стороны AC;
б) уравнение медианы AM;
в) уравнение высоты BH и найти её длину.

Решение

а)
Уравнение АС как уравнение прямой, проходящей через две точки имеет вид:
(x-x_(C))/(x_(A)-x_(C))=(y-y_(C))/(y_(A)-y_(C))

(x-17)/(-1-17)=(y-10)/(7-10)
Пропорция, перемножаем крайние и средние члены пропорции
-3*(х-17)=-18*(у-10)
х-17=6(у-10)
х-6у+43=0
б)
х_(М)=(х_(В)+х_(С))/2=(11+17)/2=14
у_(М)=(у_(В)+у_(С))/2=(2+10)/2=6
M(14;6)
Уравнение АМ как уравнение прямой, проходящей через две точки имеет вид
(x-x_(M))/(x_(A)-x_(M))=(y-y_(M))/(y_(A)-y_(M))
(x-14)/(-1-14)=(y-6)/(7-6)
или
х-14=-15(у-6)
х+15у-104=0
в) ВН ⊥ АС
Угловые коэффициенты взаимно перпендикулярных прямых равны -1
Так как уравнение АС имеет вид
у=(1/6) х-(43/6)

у=-6х+b — уравнение прямых, перпендикулярных АС
Уравнение ВН найдем подставив координаты точки В в данное семейство
2=-6*11+b
b=68
y=-6x+68

или второй способ направляющие векторы взаимно перпендикулярных прямых тоже взаимно перпендикулярны.
Направляющий вектор АС имеет координаты.
(1;-6)
Направляющий вектор ВН имеет координаты (6;1)
Тогда их скалярное произведение (1*6-6*1=0)
6х+у+m=0
Подставляем координаты точки В
6*11+2=m
m=-68
6х+у-68=0

ВН=d( расстоянию от точки В до АС)=
=|11-6*2+43|/sqrt(1+6^2)=
=42/sqrt(37)

Медиана треугольника

Определение . Медианой треугольника называют отрезок, соединяющий вершину треугольника с серединой противоположной стороны (рис 1).

Поскольку в каждом треугольнике имеется три вершины, то в каждом треугольнике можно провести три медианы.

На рисунке 1 медианой является отрезок BD .

Утверждение 1 . Медиана треугольника делит его на два треугольника равной площади ( равновеликих треугольника).

Доказательство . Проведем из вершины B треугольника ABC медиану BD и высоту BE (рис. 2),

и заметим, что (см. раздел нашего справочника «Площадь треугольника»)

Поскольку отрезок BD является медианой, то

что и требовалось доказать.

Утверждение 2 . Точка пересечения двух любых медиан треугольника делит каждую из этих медиан в отношении 2 : 1 , считая от вершины треугольника.

Доказательство . Рассмотрим две любых медианы треугольника, например, медианы AD и CE , и обозначим точку их пересечения буквой O (рис. 3).

Обозначим середины отрезков AO и CO буквами F и G соответственно (рис. 4).

Теперь рассмотрим четырёхугольник FEDG (рис. 5).

Сторона ED этого четырёхугольника является средней линией в треугольнике ABC . Следовательно,

Сторона FG четырёхугольника FEDG является средней линией в треугольнике AOC . Следовательно,

Отсюда вытекает, что точка O делит каждую из медиан AD и CE в отношении 2 : 1 , считая от вершины треугольника.

Следствие . Все три медианы треугольника пересекаются в одной точке.

Доказательство . Рассмотрим медиану AD треугольника ABC и точку O , которая делит эту медиану в отношении 2 : 1 , считая от вершины A (рис.7).

Поскольку точка, делящая отрезок в заданном отношении, является единственной, то и другие медианы треугольника будут проходить через эту точку, что и требовалось доказать.

Определение . Точку пересечения медиан треугольника называют центроидом треугольника.

Утверждение 3 . Медианы треугольника делят треугольник на 6 равновеликих треугольников (рис. 8).

Доказательство . Докажем, что площадь каждого из шести треугольников, на которые медианы разбивают треугольник ABC , равна площади треугольника ABC. Для этого рассмотрим, например, треугольник AOF и опустим из вершины A перпендикуляр AK на прямую BF (рис. 9).