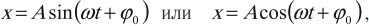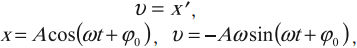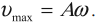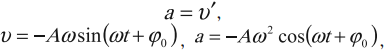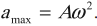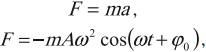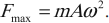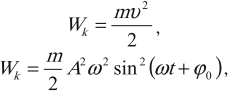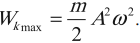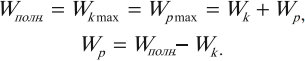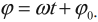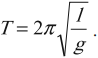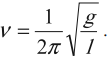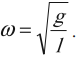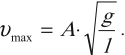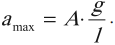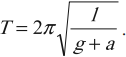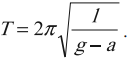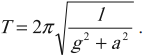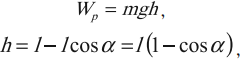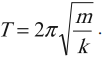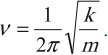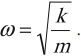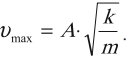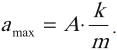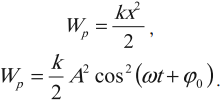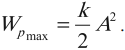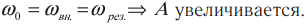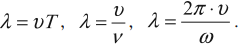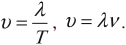Уравнение механических колебаний 10 класс

Механические колебания и волны

Механические колебания – периодически повторяющееся перемещение материальной точки, при котором она движется по какой-либо траектории поочередно в двух противоположных направлениях относительно положения устойчивого равновесия.

Отличительными признаками колебательного движения являются:

• повторяемость движения;
• возвратность движения.

Для существования механических колебаний необходимо:

• наличие возвращающей силы – силы, стремящейся вернуть тело в положение равновесия (при малых смещениях от положения равновесия);
• наличие малого трения в системе.

Механические волны – это процесс распространения колебаний в упругой среде.

Виды волн

• Поперечная – это волна, в которой колебание частиц среды происходит перпендикулярно направлению распространения волны.

Поперечная волна представляет собой чередование горбов и впадин.
Поперечные волны возникают вследствие сдвига слоев среды относительно друг друга, поэтому они распространяются в твердых телах.

• Продольная – это волна, в которой колебание частиц среды происходит в направлении распространения волны.

Продольная волна представляет собой чередование областей уплотнения и разряжения.
Продольные волны возникают из-за сжатия и разряжения среды, поэтому они могут возникать в жидких, твердых и газообразных средах.

Важно!
Механические волны не переносят вещество среды. Они переносят энергию, которая складывается из кинетической энергии движения частиц среды и потенциальной энергии ее упругой деформации.

Гармонические колебания

Гармонические колебания – простейшие периодические колебания, при которых координата тела меняется по закону синуса или косинуса:

где ​ \( x \) ​ – координата тела – смещение тела от положения равновесия в данный момент времени; ​ \( A \) ​ – амплитуда колебаний; ​ \( \omega t+\varphi_0 \) ​ – фаза колебаний; ​ \( \omega \) ​ – циклическая частота; ​ \( \varphi_0 \) ​ – начальная фаза.

Если в начальный момент времени тело проходит положение равновесия, то колебания являются синусоидальными.

Если в начальный момент времени смещение тела совпадает с максимальным отклонением от положения равновесия, то колебания являются косинусоидальными.

Скорость гармонических колебаний
Скорость гармонических колебаний есть первая производная координаты по времени:

где ​ \( v \) ​ – мгновенное значение скорости, т. е. скорость в данный момент времени.

Амплитуда скорости – максимальное значение скорости колебаний, это величина, стоящая перед знаком синуса или косинуса:

Ускорение гармонических колебаний
Ускорение гармонических колебаний есть первая производная скорости по времени:

где ​ \( a \) ​ – мгновенное значение ускорения, т. е. ускорение в данный момент времени.

Амплитуда ускорения – максимальное значение ускорения, это величина, стоящая перед знаком синуса или косинуса:

Если тело совершает гармонические колебания, то сила, действующая на тело, тоже изменяется по гармоническому закону:

где ​ \( F \) ​ – мгновенное значение силы, действующей на тело, т. е. сила в данный момент времени.

Амплитуда силы – максимальное значение силы, величина, стоящая перед знаком синуса или косинуса:

Тело, совершающее гармонические колебания, обладает кинетической или потенциальной энергией:

где ​ \( W_k \) ​ – мгновенное значение кинетической энергии, т. е. кинетическая энергия в данный момент времени.

Амплитуда кинетической энергии – максимальное значение кинетической энергии, величина, стоящая перед знаком синуса или косинуса:

При гармонических колебаниях каждую четверть периода происходит переход потенциальной энергии в кинетическую и обратно.
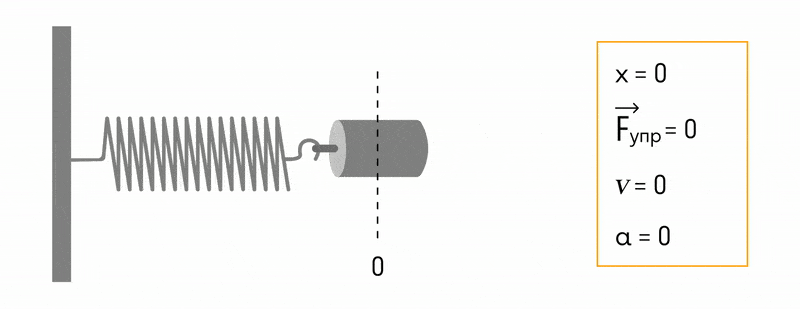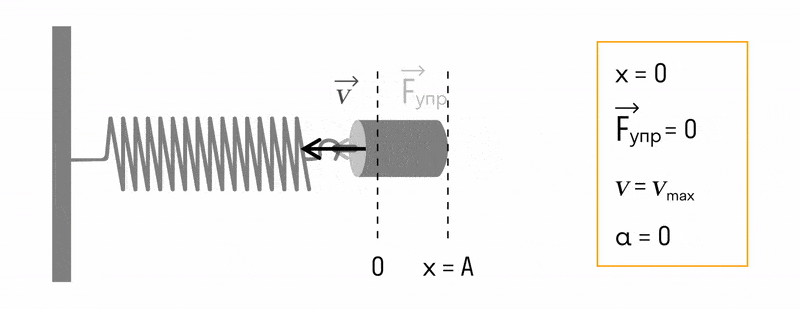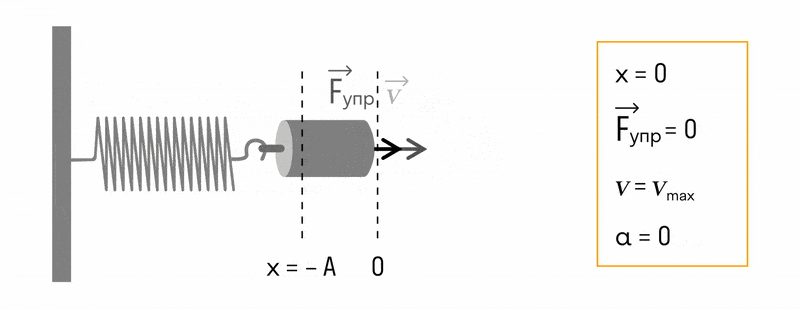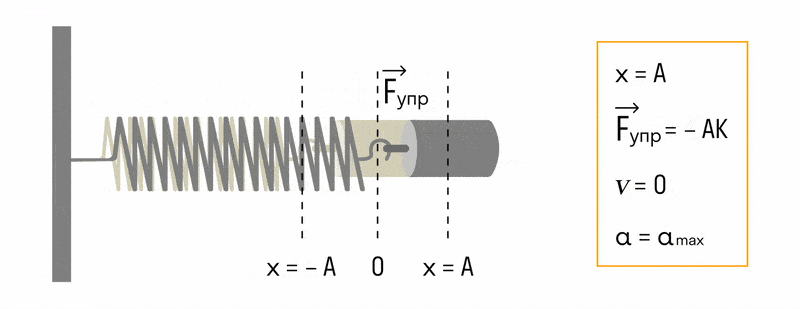
В положении равновесия:

• потенциальная энергия равна нулю;
• кинетическая энергия максимальна.

При максимальном отклонении от положения равновесия:

• кинетическая энергия равна нулю;
• потенциальная энергия максимальна.

Полная механическая энергия гармонических колебаний
При гармонических колебаниях полная механическая энергия равна сумме кинетической и потенциальной энергий в данный момент времени:

Важно!
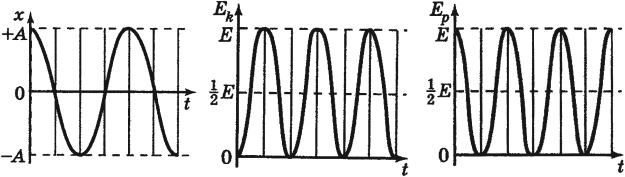
Следует помнить, что период колебаний кинетической и потенциальной энергий в 2 раза меньше, чем период колебаний координаты, скорости, ускорения и силы. А частота колебаний кинетической и потенциальной энергий в 2 раза больше, чем частота колебаний координаты, скорости, ускорения и силы.

Графики зависимости кинетической, потенциальной и полной энергий всегда лежат выше оси времени.

Если сила сопротивления отсутствует, то полная энергия сохраняется. График зависимости полной энергии от времени есть прямая, параллельная оси времени (в отсутствие сил трения).

Амплитуда и фаза колебаний

Амплитуда колебаний – модуль наибольшего смещения тела от положения равновесия.
Обозначение – ​ \( A\, (X_) \) ​, единицы измерения – м.

Фаза колебаний – это величина, которая определяет состояние колебательной системы в любой момент времени.
Обозначение – ​ \( \varphi \) ​, единицы измерения – рад (радиан).

Фаза колебаний – это величина, стоящая под знаком синуса или косинуса. Она показывает, какая часть периода прошла от начала колебаний.
Фаза гармонических колебаний в процессе колебаний изменяется.
​ \( \varphi_0 \) ​ – начальная фаза колебаний.
Начальная фаза колебаний – величина, которая определяет положение тела в начальный момент времени.

Важно!
Путь, пройденный телом за одно полное колебание, равен четырем амплитудам.

Период колебаний

Период колебаний – это время одного полного колебания.
Обозначение – ​ \( T \) ​, единицы измерения – с.

Период гармонических колебаний – постоянная величина.

Частота колебаний

Частота колебаний – это число полных колебаний в единицу времени.
Обозначение – ​ \( \nu \) ​, единицы времени – с -1 или Гц (Герц).

1 Гц – это частота такого колебательного движения, при котором за каждую секунду совершается одно полное колебание:

Период и частота колебаний – взаимно обратные величины:

Циклическая частота – это число колебаний за 2π секунд.
Обозначение – ​ \( \omega \) ​, единицы измерения – рад/с.

Свободные колебания (математический и пружинный маятники)

Свободные колебания – колебания, которые совершает тело под действием внутренних сил системы за счет начального запаса энергии после того как его вывели из положения устойчивого равновесия.

Условия возникновения свободных колебаний:

• при выведении тела из положения равновесия должна возникнуть сила, стремящаяся вернуть его в положение равновесия;
• силы трения в системе должны быть достаточно малы. При наличии сил трения свободные колебания будут затухающими.

При наличии сил трения свободные колебания будут затухающими.
Затухающие колебания – это колебания, амплитуда которых с течением времени уменьшается.

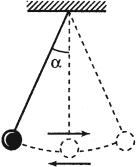
Математический маятник – это материальная точка, подвешенная на невесомой нерастяжимой нити.

Период колебаний математического маятника:

Частота колебаний математического маятника:

Циклическая частота колебаний математического маятника:

Максимальное значение скорости колебаний математического маятника:

Максимальное значение ускорения колебаний математического маятника:

Период свободных колебаний математического маятника, движущегося вверх с ускорением или вниз с замедлением:

Период свободных колебаний математического маятника, движущегося вниз с ускорением или вверх с замедлением:

Период свободных колебаний математического маятника, горизонтально с ускорением или замедлением:

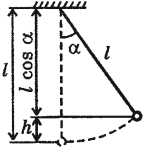
Мгновенное значение потенциальной энергии математического маятника, поднявшегося в процессе колебаний на высоту ​ \( h \) ​, определяется по формуле:

где ​ \( l \) ​ – длина нити, ​ \( \alpha \) ​ – угол отклонения от вертикали.

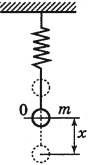
Пружинный маятник – это тело, подвешенное на пружине и совершающее колебания вдоль вертикальной или горизонтальной оси под действием силы упругости пружины.

Период колебаний пружинного маятника:

Частота колебаний пружинного маятника:

Циклическая частота колебаний пружинного маятника:

Максимальное значение скорости колебаний пружинного маятника:

Максимальное значение ускорения колебаний пружинного маятника:

Мгновенную потенциальную энергию пружинного маятника можно найти по формуле:

Амплитуда потенциальной энергии – максимальное значение потенциальной энергии, величина, стоящая перед знаком синуса или косинуса:

Важно!
Если маятник не является ни пружинным, ни математическим (физический маятник), то его циклическую частоту, период и частоту колебаний по формулам, применимым к математическому и пружинному маятнику, рассчитать нельзя. В данном случае эти величины рассчитываются из формулы силы, действующей на маятник, или из формул энергий.

Вынужденные колебания

Вынужденные колебания – это колебания, происходящие под действием внешней периодически изменяющейся силы.

Вынужденные колебания, происходящие под действием гармонически изменяющейся внешней силы, тоже являются гармоническими и незатухающими. Их частота равна частоте внешней силы и называется частотой вынужденных колебаний.

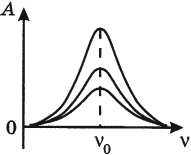
Резонанс

Резонанс – явление резкого возрастания амплитуды колебаний, которое происходит при совпадении частоты вынуждающей силы и собственной частоты колебаний тела.

​ \( v_0 \) ​ – собственная частота колебаний маятника.

На рисунке изображены резонансные кривые для сред с разным трением. Чем меньше трение, тем выше и острее резонансная кривая.

Явление резонанса учитывается при периодически изменяющихся нагрузках в машинах и различных сооружениях.
Также резонанс используется в акустике, радиотехнике и т. д.

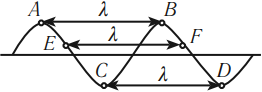
Длина волны

Длина волны – это расстояние, на которое волна распространяется за один период, т. е. это кратчайшее расстояние между двумя точками среды, колеблющимися в одинаковых фазах.
Обозначение – ​ \( \lambda \) ​, единицы измерения – м.

Расстояние между соседними гребнями или впадинами в поперечной волне и между соседними сгущениями или разряжениями в продольной волне равно длине волны.

Скорость распространения волны – это скорость перемещения горбов и впадин в поперечной волне и сгущений или разряжений в продольной волне.

Звук – это колебания упругой среды, воспринимаемые органом слуха.

Условия, необходимые для возникновения и ощущения звука:

• наличие источника звука;
• наличие упругой среды между источником и приемником звука;
• наличие приемника звука; • частота колебаний должна лежать в звуковом диапазоне;
• мощность звука должна быть достаточной для восприятия.

Звуковые волны – это упругие волны, вызывающие у человека ощущение звука, представляющие собой зоны сжатия и разряжения, передающиеся на расстояние с течением времени.

Классификация звуковых волн:

• инфразвук (​ \( \nu \) ​ \( \nu \) \( \nu \) > 20 000 Гц).

Скорость звука – это скорость распространения фазы колебания, т. е. области сжатия и разряжения среды.

Скорость звука зависит

• от упругих свойств среды:

в воздухе – 331 м/с, в воде – 1400 м/с, в металле – 5000 м/с;

в воздухе при температуре 0°С – 331 м/с,
в воздухе при температуре +15°С – 340 м/с.

Характеристики звуковой волны

• Громкость – это величина, характеризующая слуховые ощущения человека, зависящая от амплитуды колебаний в звуковой волне. Единицы измерения – дБ (децибел).
• Высота тона – это величина, характеризующая слуховые ощущения человека, зависящая от частоты колебаний в звуковой волне. Чем больше частота, тем выше звук. Чем меньше частота, тем ниже звук.
• Тембр – это окраска звука.

Музыкальный звук – это звук, издаваемый гармонически колеблющимся телом. Каждому музыкальному тону соответствует определенная длина и частота звуковой волны.
Шум – хаотическая смесь тонов.

Гармонические колебания

О чем эта статья:

9 класс, 11 класс, ЕГЭ/ОГЭ

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Механические колебания

Механические колебания — это физические процессы, которые точно или приблизительно повторяются через одинаковые интервалы времени.

Колебания делятся на два вида: свободные и вынужденные.

Свободные колебания

Это колебания, которые происходят под действием внутренних сил в колебательной системе.

Они всегда затухающие, потому что весь запас энергии, сообщенный в начале, в конце уходит на совершение работы по преодолению сил трения и сопротивления среды (в этом случае механическая энергия переходит во внутреннюю). Из-за этого свободные колебания почти не имеют практического применения.

Вынужденные колебания

А вот вынужденные колебания восполняют запас энергии внешним воздействием. Если это происходит каждый период, то колебания вообще затухать не будут.

Вынужденные колебания — это колебания, которые происходят под действием внешней периодически меняющейся силы.

Частота, с которой эта сила воздействует, равна частоте, с которой система будет колебаться.

Например, качели. Если вас кто-то будет на них качать, каждый раз давая толчок, когда вы приходите в одну и ту же точку — такое колебание будет считаться вынужденным.

Это колебание все еще будет считаться вынужденным, если вас будут раскачивать из положения равновесия. Просто в данном случае амплитуда (о которой речь пойдет чуть ниже) будет увеличиваться с каждым колебанием.

Автоколебания

Иногда вынужденному колебанию не нужно внешнего воздействия, чтобы случиться. Бывают такие системы, в которых это внешние воздействие возникает само из-за способности регулировать поступление энергии от постоянного источника.

У автоколебательной системы есть три важных составляющих:

• сама колебательная система
• источник энергии
• устройство обратной связи, обеспечивающей связь между источником и системой

Часы с кукушкой — пример автоколебательной системы. Гиря на ниточке (цепочке) стремится вращать зубчатое колесо (храповик). При колебаниях маятника анкер цепляет за зубец, и вращение приостанавливается.

Но в результате маятник получает толчок, компенсирующий потери энергии из-за трения. Потенциальная энергия гири, которая постепенно опускается, расходуется на поддержание незатухающих колебаний.

Характеристики колебаний

Чтобы перейти к гармоническим колебаниям, нам нужно описать величины, которые помогут нам эти колебания охарактеризовать. Любое колебательное движение можно описать величинами: период, частота, амплитуда, фаза колебаний.

Период — это время одного полного колебания. Измеряется в секундах и обозначается буквой T.

Формула периода колебаний

T = t/N

N — количество колебаний [—]

Также есть величина, обратная периоду — частота. Она показывает, сколько колебаний совершает система в единицу времени.

Формула частоты

ν = N/t = 1/T

N — количество колебаний [—]

Амплитуда — это максимальное отклонение от положения равновесия. Измеряется в метрах и обозначается либо буквой A, либо x max .

Она используется в уравнении гармонических колебаний:

Гармонические колебания

Простейший вид колебательного процесса — простые гармонические колебания, которые описывают уравнением:

Уравнение гармонических колебаний

x — координата в момент времени t [м]

t — момент времени [с]

(2πνt) в этом уравнении — это фаза. Ее обозначают греческой буквой φ

Фаза колебаний

t — момент времени [с]

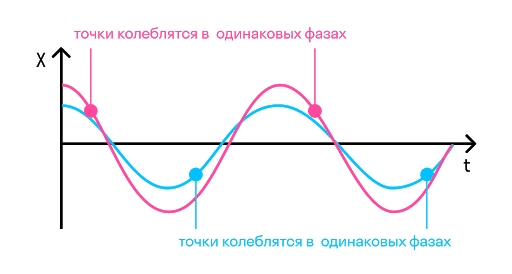
Фаза колебаний — это физическая величина, которая показывает отклонение точки от положения равновесия. Посмотрите на рисунок, на нем изображены одинаковые фазы:

Например, в тех же самых часах с кукушкой маятник совершает колебания. Он качается слева направо и приходит в самую правую точку. В той же фазе он будет находиться, когда придет в ту же точку, идя справа налево. Если мы возьмем точку на сантиметр левее самой правой, то идя в нее не слева направо, а справа налево, мы получим уже другую фазу.

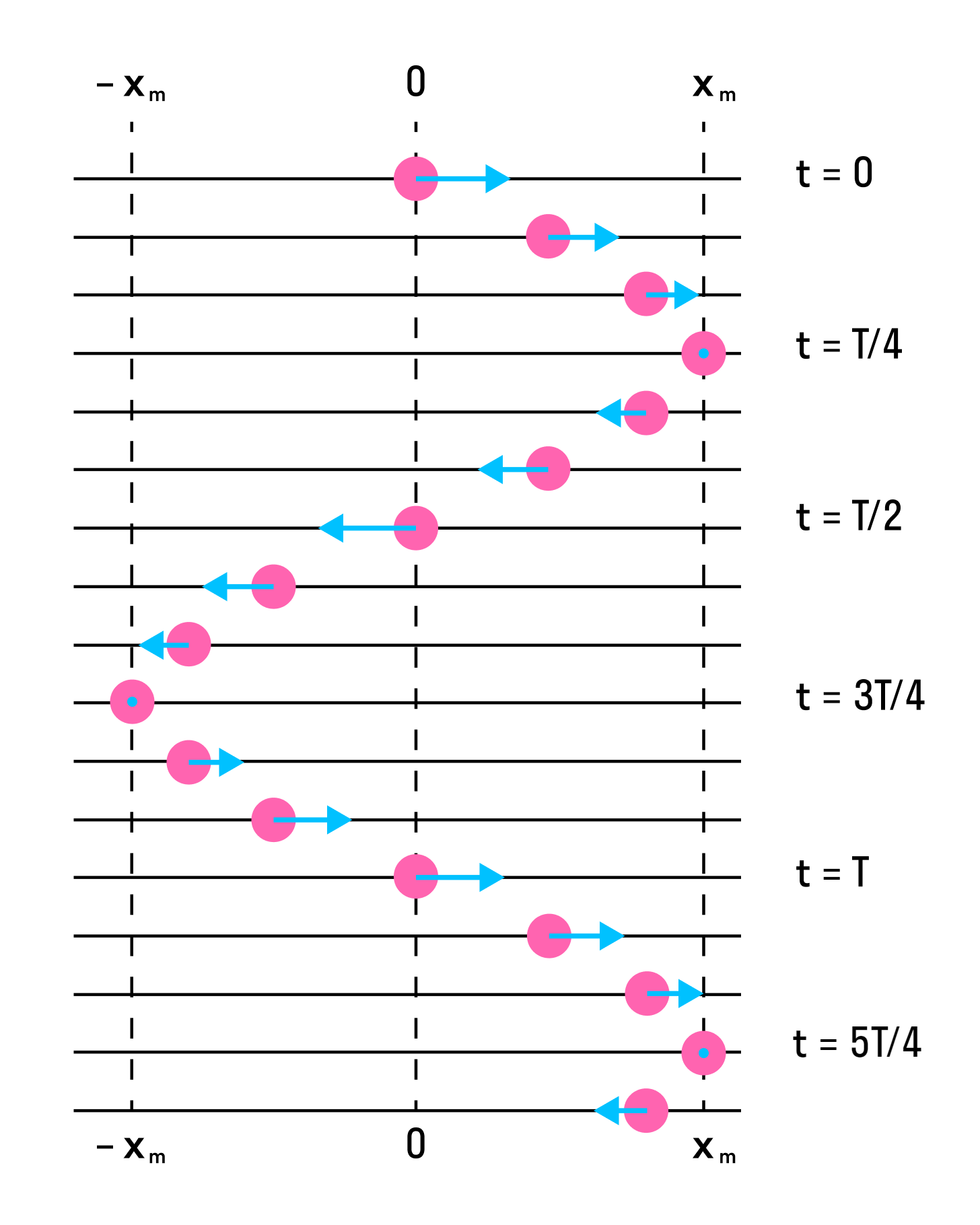
На рисунке ниже показаны положения тела через одинаковые промежутки времени при гармонических колебаниях. Такую картину можно получить при освещении колеблющегося тела короткими периодическими вспышками света (стробоскопическое освещение). Стрелки изображают векторы скорости тела в различные моменты времени.

Если изменить период, начальную фазу или амплитуду колебания, графики тоже изменятся.

На рисунке ниже во всех трех случаях для синих кривых начальная фаза равна нулю, а в последнем (с) — красная кривая имеет меньшую начальную фазу.

В первом случае (а) красная кривая описывает колебание, у которого амплитуда больше колебания, описанного синей линией.

Во втором случае (b) красная кривая отличается от синей только значением периода — у красной период в два раза меньше.

Математический маятник

Математический маятник — отличный пример гармонических колебаний. Если мы подвесим шарик на нити, то это еще не будет математическим маятником — пока он только физический.

Математическим этот маятник станет, если размеры шарика много меньше длины нити (тогда этими размерами можно пренебречь и рассматривать шарик как материальную точку), растяжение нити очень мало, а масса нити во много раз меньше массы шарика.

Математическим маятником называется система, которая состоит из материальной точки массой m и невесомой нерастяжимой нити длиной l, на которой материальная точка подвешена, и которая находится в поле силы тяжести (или других сил).

Период малых колебаний математического маятника в поле силы тяжести Земли определяется по формуле:

Формула периода колебания математического маятника

l — длина нити [м]

g — ускорение свободного падения [м/с 2 ]

На планете Земля g = 9,8 м/с 2

Пружинный маятник

Пружинный маятник — это груз, прикрепленный к пружине, массой которой можно пренебречь.

В пружинном маятнике колебания совершаются под действием силы упругости.
Пока пружина не деформирована, сила упругости на тело не действует.

Формула периода колебания пружинного маятника

m — масса маятника [кг]

k — жесткость пружины [Н/м]

Закон сохранения энергии для гармонических колебаний

Физика — такая клевая наука, в которой ничего не исчезает бесследно и не появляется из ниоткуда. Эту особенность описывает закон сохранения энергии.

Рассмотрим его на примере математического маятника.

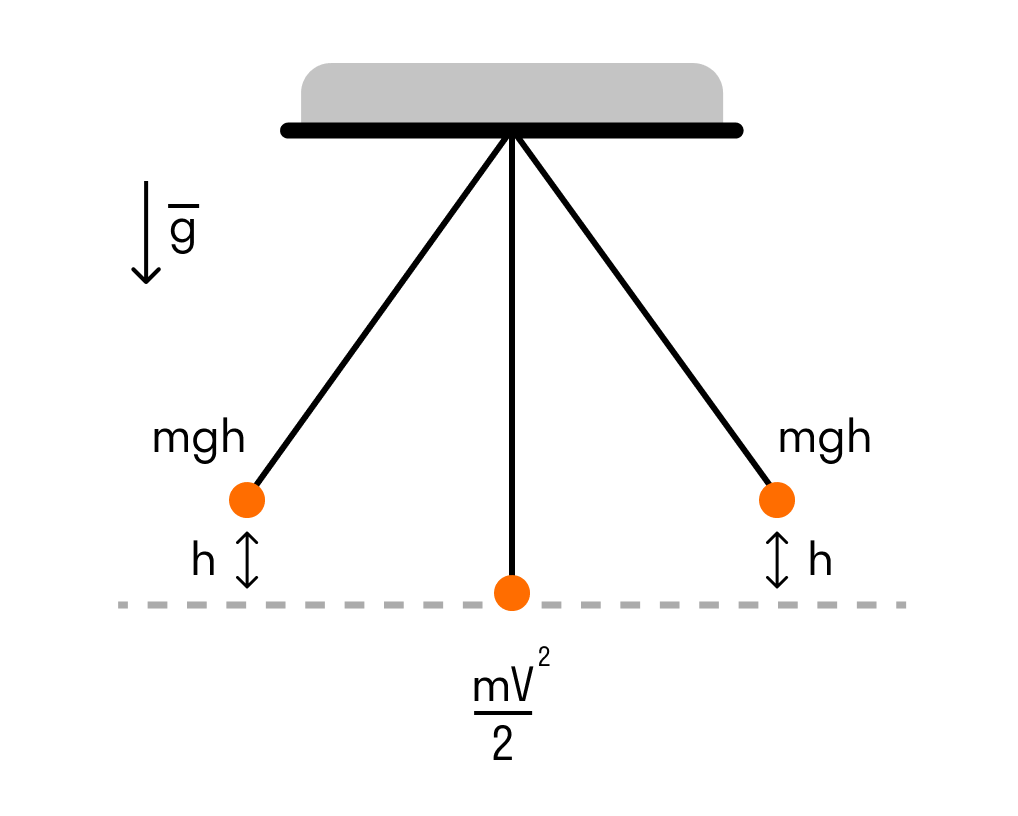
• Когда маятник отклоняют на высоту h, его потенциальная энергия максимальна.
• Когда маятник опускается, потенциальная энергия переходит в кинетическую. Причем в нижней точке, где потенциальная энергия равна нулю, кинетическая энергия максимальна и равна потенциальной энергии в верхней точке. Скорость груза в этой точке максимальна.

Онлайн-курсы физики в Skysmart не менее увлекательны, чем наши статьи!

Конспект по физике на тему «Механические колебания» (10 класс)

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Механические колебания математического и пружинного маятника. Величины, характеризующие колебания. Графическое представление колебательного движения .

Механические колебания – движения, которые точно или приблизительно точно повторяются через определенные интервалы времени. Для колебаний характерно, что колеблющееся тело попеременно смещается то в одну, то в другую сторону относительно некоторой точки или линии – положения равновесия .

Свободно колеблющиеся тела всегда взаимодействуют с другими телами и вместе с ними образуют:

Колебательная система – система тел, способная совершать свободные колебания.

Одно из основных общих свойств всех колебательных систем заключается в возникновении силы, возвращающей систему в положение устойчивого равновесия.

Рассмотрим примеры колебательных систем :

Маятник – твердое тело, совершающее под действием приложенных сил колебания около неподвижной точки или вокруг оси.

1) Математический маятник – материальная точка, подвешенная на длинной прочной нерастяжимой невесомой нити. . → модель.

В устойчивом положении равновесия силы, действующие на тело, взаимно уравновешены: сила тяжести уравновешена силой натяжения нити маятника .

Если отклонить шарик от положения равновесия, то равнодействующая сил тяжести и натяжения нити будет направлена к положению равновесия и под ее действием шарик начнет двигаться с ускорением.

В момент, когда шарик достигнет положения равновесия сумма всех сил, действующих на него, станет равной нулю. Следовательно, и ускорение шарика, согласно II закону Ньютона станет равным нулю. Но к этому моменту скорость шарика уже достигнет некоторого значения. Согласно закону инерции, любое тело обладает свойством сохранять свою скорость, если на него не действуют силы или равнодействующая сил равна нулю. Поэтому, не останавливаясь в положении равновесия, шарик по инерции будет двигаться.

После прохождения положения равновесия, равнодействующая сил, а значит и ускорение, будет направлена противоположно скорости. Следовательно, шарик будет двигаться замедленно, до тех пор, пока не остановится. После этого шарик начнет ускоренное движение в противоположную сторону.

Проскакивая по инерции положение равновесия, шарик продолжит свое движение, после чего весь колебательный процесс повторяется сначала.

При колебаниях математического маятника шарик всегда движется по дуге окружности, радиус которой равен длине нити l . Поэтому положение шарика в любой момент времени определяется углом отклонение нити от вертикали. Будем считать α положительным, если маятник отклонен вправо от положения равновесия, и отрицательным, если он отклонен влево.

Для того чтобы вывести уравнение движения математического маятника, воспользуемся II законом Ньютона:

OX:

Проекция силы тяжести на ось ОХ и будет силой, возвращающей маятник в положение равновесия. Причем эта сила всегда имеет знак, противоположный знаку угла: при отклонении маятника вправо , проекция силы тяжести на ось ОХ направлена влево ; при отклонении маятника влево , проекция силы тяжести на ось ОХ направлена вправо .

Из прямоугольного треугольника: , тогда:

Т.к. , то введем обозначение , тогда:

— уравнение колебаний математического маятника .

2) Пружинный маятник – материальная точка, подвешенная на упругой невесомой пружине. . → модель.

В устойчивом положении равновесия силы, действующие на тело, взаимно уравновешены: сила тяжести уравновешена силой упругости пружины .

Если сместить грузик вниз так, чтобы длина пружины увеличилась на x , то на тело начнет действовать дополнительная сила упругости, которая согласно закону Гука, пропорциональна удлинению пружины. Будем называть эту силу – квазиупругая сила – геометрическая сумма силы тяжести и силы упругости, действующих на пружинный маятник. Эта сила направлена вверх и под ее воздействием тело будет двигаться с ускорением, направленным вверх, постепенно увеличивая скорость. Квазиупругая сила будет при этом уменьшаться.

Дойдя до положения устойчивого равновесия, квазиупругая сила станет равной нулю, и ускорение, согласно II закону Ньютона, также станет равным нулю. Однако тело не остановится, а будет продолжать двигаться вверх по инерции.

После прохождения положения равновесия, пружина начинает сжиматься, и в результате вновь появляется квазиупругая сила, направленная уже вниз и тормозящая движение груза. Согласно II закону Ньютона, тело продолжит движение вверх с ускорением, направленным вниз, то есть замедленно. Следовательно, квазиупругая сила стремится вернуть тело в положение равновесия. Скорость убывает до тех пор, пока в самой верхней точке не обратится в ноль. При этом сжатие пружины, а, следовательно, и квазиупругая сила, увеличиваются.

После этого тело с ускорением начнет двигаться вниз. С уменьшением х модуль квазиупругой силы убывает и в положении равновесия вновь становится равным нулю. Но тело уже успевает к этому моменту набрать скорость и продолжает двигаться вниз по инерции. Это движение приводит к дальнейшему растяжению пружины. Движение груза тормозиться до полной остановки в крайнем нижнем положении, после чего весь процесс повторяется сначала.

Воспользуемся II законом Ньютона для движения пружинного маятника под действием квазиупругой силы:

OX: . Согласно закону Гука:

Уравнение движения не содержит силы тяжести. Дело в том, что сила тяжести, действуя на груз, вызывает растяжение пружины на постоянную величину. Но это не влияет на характер движения груза.

Т.к. , то введем обозначение , тогда:

— уравнение колебаний пружинного маятника .

Вывод : уравнения движения, описывающие колебания таких различных систем, как груз на пружине и математический маятник, одинаковы. Следовательно, движения этих колебательных систем происходят одинаковым образом. Смещения груза на пружине и шарика маятника от положения равновесия изменяются со временем по одному и тому же закону, несмотря на то, что силы, вызывающие колебания, имеют различную физическую природу. В первом случае это квазиупругая сила, во втором – составляющая силы тяжести.

Величины, характеризующие колебательное движение:

1) Амплитуда (х₀) – модуль наибольшего смещения тела от положения равновесия.

Амплитуда определяется начальными условиями.

При колебаниях движение тела периодически повторяется. Колеблющееся тело совершает одно полное колебание, если проходит путь, равный четырем амплитудам.

2) Период ( T ) – минимальный промежуток времени, через который движение тела полностью повторяется.

t – время колебаний; N – число полных колебаний.

3) Частота (ν) – число колебаний в единицу времени.

Си: [ ν ] → 1/с = 1Гц.

4) Циклическая (круговая) частота (ω₀) – число колебаний за 2π секунд.

Си: [ ] → 1 рад/с

Эту частоту называют:

Собственная частота (ω₀) – частота свободных колебаний.

Согласно уравнению колебаний математического маятника, эта величина равна:

Период колебаний математического маятника зависит :

1) От длины маятника .

Чем больше длина маятника, тем медленнее происходят его колебания. Маятник 1 колеблется медленнее маятника 2.

2) От ускорения свободного падения .

Чем меньше ускорение свободного падения, тем больше период колебаний маятника, и, следовательно, тем медленнее идут часы с маятником. Так часы с маятником в виде груз на стержне отстанут за счет уменьшения ускорения свободного падения с высотой в сутки почти на 7с, если их поднять на вершину Останкинской телебашни (500м).

Период колебаний математического маятника не зависит:

1) От массы маятника .

Маятники 1 и 2 будут совершать одинаковое число колебаний в единицу времени.

1) От амплитуды колебаний (при малых углах отклонения) .

Это свойство независимости периода колебаний от амплитуды называют изохронность .

Пусть амплитуда колебаний увеличилась в 2 раза → сила, возвращающая тело в положение равновесия увеличилась в 2 раза → ускорение, вызванное этой силой, увеличилось в 2 раза → приобретенная скорость станет больше в два раза → за то же время тело пройдет вдвое больший путь к положению равновесия, что и при колебаниях вдвое меньшей амплитуды.

Согласно уравнению колебаний пружинного маятника, собственная частота равна:

Период колебаний пружинного маятника зависит :

1) От массы маятника .

Чем больше масса маятника, тем медленнее он изменяет свою скорость под действием силы, тем медленнее происходят его колебания. Маятник 1 колеблется медленнее маятника 2.

2) От жесткости пружины .

Более жесткая пружина сообщает телу большее ускорение, т.е. быстрее меняет его скорость и, следовательно, уменьшает время одного колебания. Маятник 1 колеблется медленнее маятника 2.

Период колебаний математического маятника не зависит:

1) От амплитуды колебаний (при упругих деформациях) .

5) Фаза колебаний (φ) – физическая величина, однозначно определяющая положение колебательной системы в любой момент времени.

Си: [ ] → 1 рад

Проведем вспомогательную окружность радиуса x ₀ . Спроецируем начальное положение тела, и положение тела в момент времени t на эту окружность.

Фаза характеризует смещение от положения равновесия (ПР) (или от начального положения) и равна углу между двумя положениями тела на вспомогательной окружности Фаза отсчитывается против часовой стрелки.

;

Начальная фаза колебаний (φ₀) – фаза колебаний в начальный момент времени ( t =0).

Пусть маятники колеблются с одинаковой частотой и одинаковыми амплитудами. Различают следующие случаи:

В любой момент времени скорости маятников направлены в противоположные стороны → колебания происходят в противоположных фазах.

В любой момент времени скорости маятников направлены в одну сторону → колебания происходят в одинаковых фазах.

В некоторый момент времени направления скоростей маятников совпадают. Через какое-то время скорости направлены в разные стороны → колебания происходят с разностью фаз.

Основная задача механики заключается в нахождении положения тела в любой момент времени. Следовательно, необходимо получить зависимость х=х( t ) для математического и пружинного маятников. Для этого необходимо решить уравнение колебаний. Однако математическое решение этих уравнение – задача сложная и требует знаний высшей математики.

Для нахождения зависимости координаты от времени обратимся к вспомогательной окружности. Для математического маятника из прямоугольного треугольника:

Для пружинного маятника из прямоугольного треугольника:

Полученную зависимость можно доказать экспериментально. Для этого массивный сосуд с маленьким отверстием снизу подвешивают на нити. Под сосудом находится длинная бумажная лента. В сосуд насыпают песок и приводят в колебательное движение. Если ленту перемещать с постоянной скоростью в направлении, перпендикулярном плоскости колебаний, то на ней останется волнообразная дорожка песка, каждая точка которой соответствует положению колеблющегося груза в тот момент, когда он проходил над ней. Полученная кривая называется синусоидой. Аналогичная кривая получается для груза, подвешенного на пружине.

Гармонические колебания – периодические изменения физической величины в зависимости от времени по закону синуса или косинуса.

Гармонические колебания происходят под действием силы, пропорциональной смещению колеблющейся точки и направленной противоположно этому смещению.

Таким образом, решением уравнения колебания пружинного и математического маятников является функция:

либо

где — фаза колебаний.

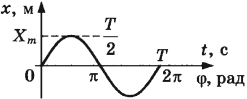
Данную зависимость можно представить графически. График зависимости координаты тела от времени имеет вид:

Наибольшие отклонения груза от положения равновесия в обе стороны одинаковы по модулю и равны х₀. Маятник начал движение из крайней точки с координатой х = х₀. За время, равное периоду, маятник совершил полное колебание, т.е., миновав положение равновесия, дошел до противоположной крайней точки с координатой – х₀, на мгновенье задержался в ней, изменил направление скорости на противоположное, затем пошел в обратном направлении и, вторично пройдя через положение равновесия, вернулся в то же самое место, откуда начал движение. Затем колебания повторяются.

При колебательном движении маятников скорость и ускорение меняются со временем (т.е. движение не является равноускоренным), так как меняется величина и направление силы, возвращающей тело в положение равновесия. Рассмотрим характер этого изменения для математического маятника. В начальный момент времени маятник отклонили от положения равновесия.