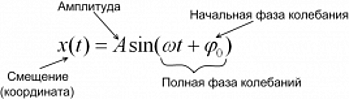Гармонические колебания
О чем эта статья:
9 класс, 11 класс, ЕГЭ/ОГЭ
Механические колебания
Механические колебания — это физические процессы, которые точно или приблизительно повторяются через одинаковые интервалы времени.
Колебания делятся на два вида: свободные и вынужденные.
Свободные колебания
Это колебания, которые происходят под действием внутренних сил в колебательной системе.
Они всегда затухающие, потому что весь запас энергии, сообщенный в начале, в конце уходит на совершение работы по преодолению сил трения и сопротивления среды (в этом случае механическая энергия переходит во внутреннюю). Из-за этого свободные колебания почти не имеют практического применения.
Вынужденные колебания
А вот вынужденные колебания восполняют запас энергии внешним воздействием. Если это происходит каждый период, то колебания вообще затухать не будут.
Вынужденные колебания — это колебания, которые происходят под действием внешней периодически меняющейся силы.
Частота, с которой эта сила воздействует, равна частоте, с которой система будет колебаться.
Например, качели. Если вас кто-то будет на них качать, каждый раз давая толчок, когда вы приходите в одну и ту же точку — такое колебание будет считаться вынужденным.
Это колебание все еще будет считаться вынужденным, если вас будут раскачивать из положения равновесия. Просто в данном случае амплитуда (о которой речь пойдет чуть ниже) будет увеличиваться с каждым колебанием.
Автоколебания
Иногда вынужденному колебанию не нужно внешнего воздействия, чтобы случиться. Бывают такие системы, в которых это внешние воздействие возникает само из-за способности регулировать поступление энергии от постоянного источника.
У автоколебательной системы есть три важных составляющих:
- сама колебательная система
- источник энергии
- устройство обратной связи, обеспечивающей связь между источником и системой
Часы с кукушкой — пример автоколебательной системы. Гиря на ниточке (цепочке) стремится вращать зубчатое колесо (храповик). При колебаниях маятника анкер цепляет за зубец, и вращение приостанавливается.
Но в результате маятник получает толчок, компенсирующий потери энергии из-за трения. Потенциальная энергия гири, которая постепенно опускается, расходуется на поддержание незатухающих колебаний.
Характеристики колебаний
Чтобы перейти к гармоническим колебаниям, нам нужно описать величины, которые помогут нам эти колебания охарактеризовать. Любое колебательное движение можно описать величинами: период, частота, амплитуда, фаза колебаний.
Период — это время одного полного колебания. Измеряется в секундах и обозначается буквой T.
Формула периода колебаний
T = t/N
N — количество колебаний [—]
Также есть величина, обратная периоду — частота. Она показывает, сколько колебаний совершает система в единицу времени.
Формула частоты
ν = N/t = 1/T
N — количество колебаний [—]
Амплитуда — это максимальное отклонение от положения равновесия. Измеряется в метрах и обозначается либо буквой A, либо x max .
Она используется в уравнении гармонических колебаний:
Гармонические колебания
Простейший вид колебательного процесса — простые гармонические колебания, которые описывают уравнением:
Уравнение гармонических колебаний
x — координата в момент времени t [м]
t — момент времени [с]
(2πνt) в этом уравнении — это фаза. Ее обозначают греческой буквой φ
Фаза колебаний
t — момент времени [с]
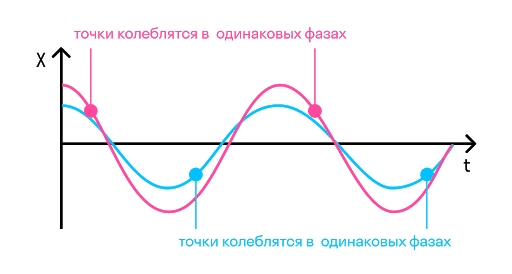
Фаза колебаний — это физическая величина, которая показывает отклонение точки от положения равновесия. Посмотрите на рисунок, на нем изображены одинаковые фазы:
Например, в тех же самых часах с кукушкой маятник совершает колебания. Он качается слева направо и приходит в самую правую точку. В той же фазе он будет находиться, когда придет в ту же точку, идя справа налево. Если мы возьмем точку на сантиметр левее самой правой, то идя в нее не слева направо, а справа налево, мы получим уже другую фазу.
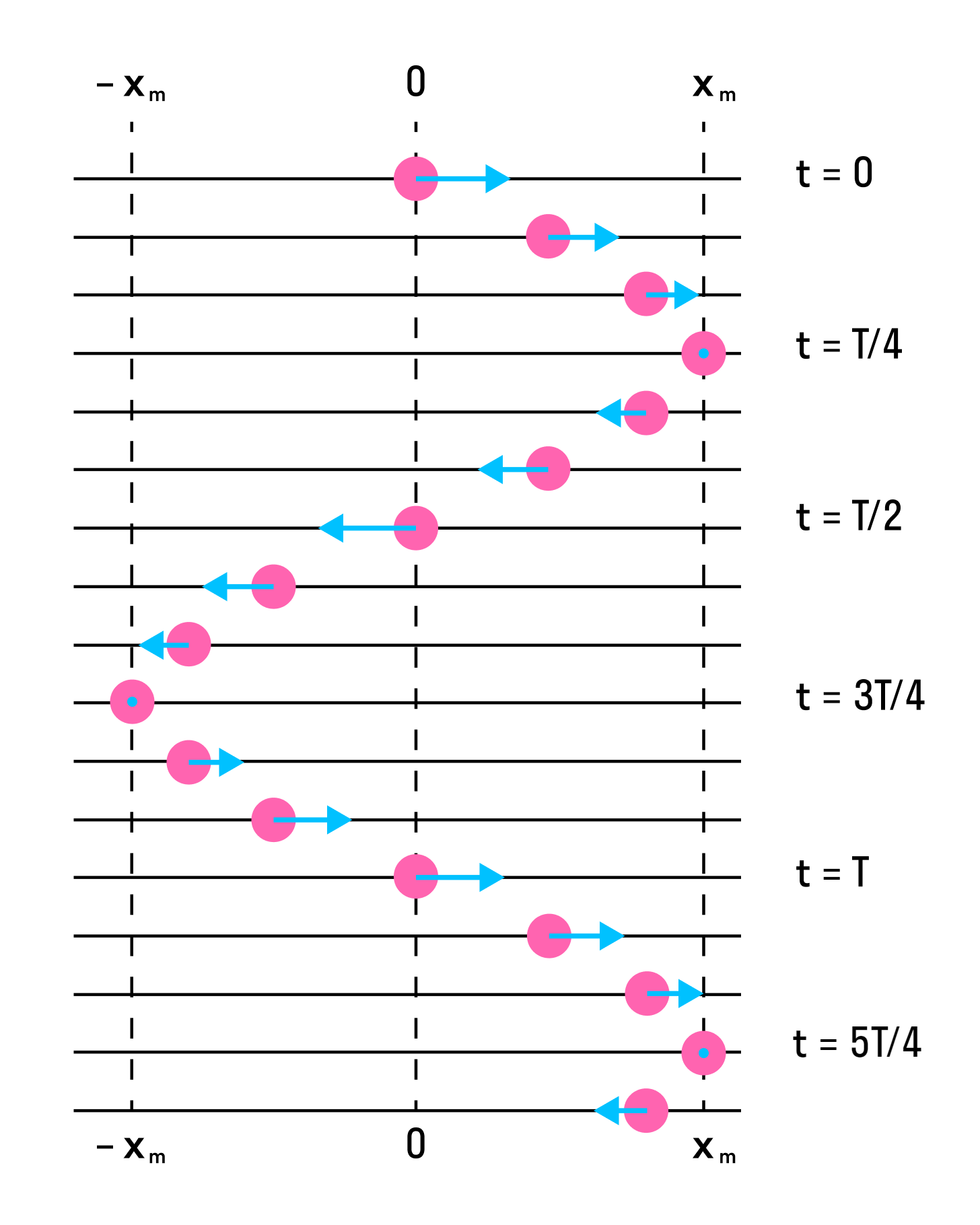
На рисунке ниже показаны положения тела через одинаковые промежутки времени при гармонических колебаниях. Такую картину можно получить при освещении колеблющегося тела короткими периодическими вспышками света (стробоскопическое освещение). Стрелки изображают векторы скорости тела в различные моменты времени.
Если изменить период, начальную фазу или амплитуду колебания, графики тоже изменятся.
На рисунке ниже во всех трех случаях для синих кривых начальная фаза равна нулю, а в последнем (с) — красная кривая имеет меньшую начальную фазу.
В первом случае (а) красная кривая описывает колебание, у которого амплитуда больше колебания, описанного синей линией.
Во втором случае (b) красная кривая отличается от синей только значением периода — у красной период в два раза меньше.
Математический маятник
Математический маятник — отличный пример гармонических колебаний. Если мы подвесим шарик на нити, то это еще не будет математическим маятником — пока он только физический.
Математическим этот маятник станет, если размеры шарика много меньше длины нити (тогда этими размерами можно пренебречь и рассматривать шарик как материальную точку), растяжение нити очень мало, а масса нити во много раз меньше массы шарика.
Математическим маятником называется система, которая состоит из материальной точки массой m и невесомой нерастяжимой нити длиной l, на которой материальная точка подвешена, и которая находится в поле силы тяжести (или других сил).
Период малых колебаний математического маятника в поле силы тяжести Земли определяется по формуле:
Формула периода колебания математического маятника
l — длина нити [м]
g — ускорение свободного падения [м/с 2 ]
На планете Земля g = 9,8 м/с 2
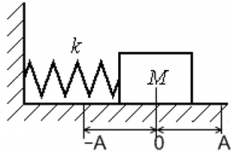
Пружинный маятник
Пружинный маятник — это груз, прикрепленный к пружине, массой которой можно пренебречь.
В пружинном маятнике колебания совершаются под действием силы упругости.
Пока пружина не деформирована, сила упругости на тело не действует.
Формула периода колебания пружинного маятника
m — масса маятника [кг]
k — жесткость пружины [Н/м]
Закон сохранения энергии для гармонических колебаний
Физика — такая клевая наука, в которой ничего не исчезает бесследно и не появляется из ниоткуда. Эту особенность описывает закон сохранения энергии.
Рассмотрим его на примере математического маятника.
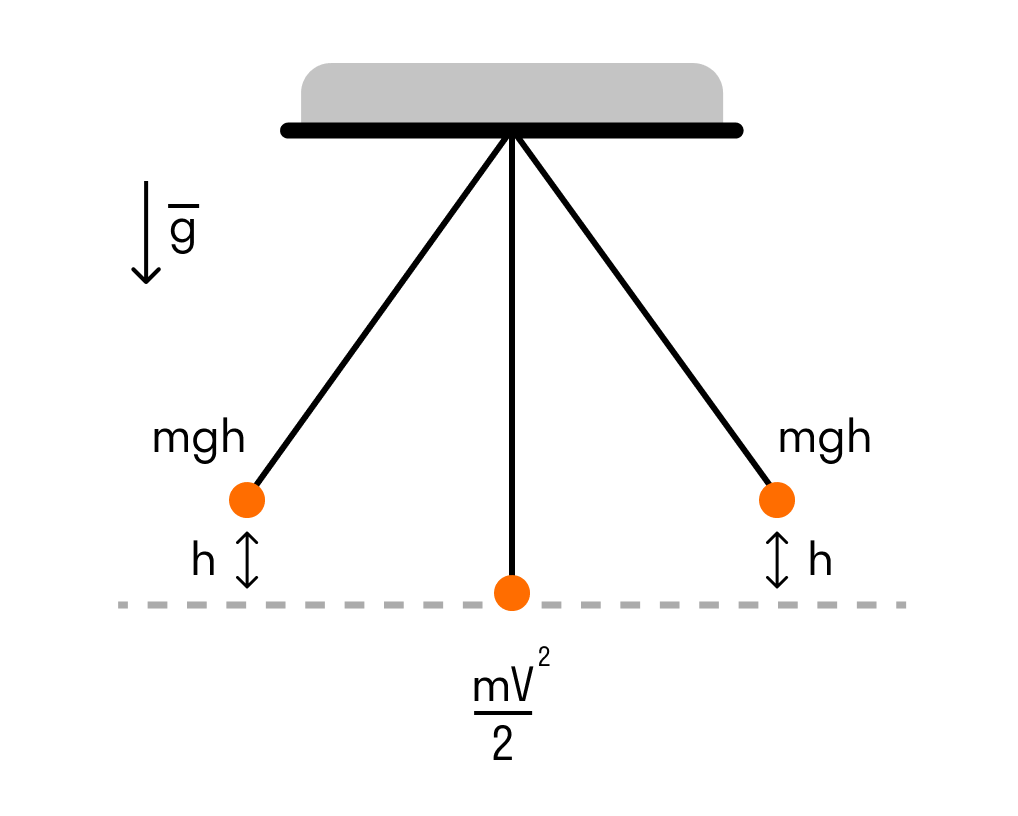
- Когда маятник отклоняют на высоту h, его потенциальная энергия максимальна.
- Когда маятник опускается, потенциальная энергия переходит в кинетическую. Причем в нижней точке, где потенциальная энергия равна нулю, кинетическая энергия максимальна и равна потенциальной энергии в верхней точке. Скорость груза в этой точке максимальна.
Онлайн-курсы физики в Skysmart не менее увлекательны, чем наши статьи!
Уравнение механических колебаний в си имеет вид
4.1.1иБТБЛФЕТЙУФЙЛЙ НЕИБОЙЮЕУЛЙИ ЛПМЕВБОЙК
рХУФШ Л РТХЦЙОЕ У ЛПЬЖЖЙГЙЕОФПН ХРТХЗПУФЙ k РТЙЛТЕРМЕО ЗТХЪ НБУУПК m, ОБИПДСЭЙКУС ОБ ЙДЕБМШОП ЗМБДЛПК РПЧЕТИОПУФЙ (ТЙУХОПЛ 4.1).

тЙУХОПЛ 4.1
рТЙ ТБУФСЦЕОЙЙ РТХЦЙОЩ ОБ ФЕМП ОБЮЙОБЕФ ДЕКУФЧПЧБФШ УЙМБ ХРТХЗПУФЙ FХРТ = — k И (УЙМБ ФСЦЕУФЙ Й УЙМБ ОПТНБМШОПК ТЕБЛГЙЙ ТБЧОЩ Й ОБРТБЧМЕОЩ Ч РТПФЙЧПРПМПЦОЩЕ УФПТПОЩ). еУМЙ ФЕМП ПФРХУФЙФШ, ФП РПД ДЕКУФЧЙЕН УЙМЩ ХРТХЗПУФЙ ПОП ОБЮЙОБЕФ ДЧЙЗБФШУС Ч УФПТПОХ, РТПФЙЧПРПМПЦОХА УНЕЭЕОЙА. рТПИПДС РПМПЦЕОЙЕ ТБЧОПЧЕУЙС, ФЕМП ВХДЕФ ПВМБДБФШ НБЛУЙНБМШОПК УЛПТПУФША Й РП ЙОЕТГЙЙ РТПДПМЦЙФ ДЧЙЦЕОЙЕ, УЦЙНБС РТХЦЙОХ. рПД ДЕКУФЧЙЕН УЙМЩ ХРТХЗПУФЙ, ЧПЪОЙЛБАЭЕК РТЙ ДЕЖПТНБГЙЙ УЦБФЙС, ФЕМП ПУФБОПЧЙФУС Й ОБЮОЕФ ДЧЙЗБФШУС Л РПМПЦЕОЙА ТБЧОПЧЕУЙС Й Ф. Д. рТЙ ЬФПН И — УНЕЭЕОЙЕ ФЕМБ ПФ РПМПЦЕОЙС ТБЧОПЧЕУЙС п -ЙЪНЕОСЕФУС РП ЪБЛПОХ
 | (4.1) |
ЗДЕ б, ω, φ0 ОЕ ЪБЧЙУСФ ПФ ЧТЕНЕОЙ. хТБЧОЕОЙЕ (4.1) ОБЪЩЧБЕФУС ХТБЧОЕОЙЕН ЛПМЕВБОЙК.
1.1 иБТБЛФЕТЙУФЙЛЙ ЗБТНПОЙЮЕУЛЙИ ЛПМЕВБОЙК
ч ХТБЧОЕОЙЙ (4.1) БНРМЙФХДБ б — НБЛУЙНБМШОПЕ ЪОБЮЕОЙЕ ЙЪНЕОСАЭЕКУС ЧЕМЙЮЙОЩ, Ч ОБЫЕН РТЙНЕТЕ б — НБЛУЙНБМШОПЕ УНЕЭЕОЙЕ ПФ РПМПЦЕОЙС ТБЧОПЧЕУЙС. бНРМЙФХДБ ЪБЧЙУЙФ ПФ ЬОЕТЗЙЙ, УППВЭЕООПК УЙУФЕНЕ Ч ОБЮБМШОЩК НПНЕОФ ЧТЕНЕОЙ (РПЛБЦЕН ОЙЦЕ). гЙЛМЙЮЕУЛБС (ЙМЙ ЛТХЗПЧБС) ЮБУФПФБ ω — ЮЙУМП РПМОЩИ ЛПМЕВБОЙК, УПЧЕТЫБЕНЩИ УЙУФЕНПК ЪБ, РТПНЕЦХФПЛ ЧТЕНЕОЙ 2π У. юБУФПФБ ν — ЮЙУМП РПМОЩИ ЛПМЕВБОЙК, УПЧЕТЫБЕНЩИ УЙУФЕНПК ЪБ 1 У. рЕТЙПД ЛПМЕВБОЙК ф — РТПНЕЦХФПЛ ЧТЕНЕОЙ, ЪБ ЛПФПТЩК УПЧЕТЫБЕФУС ПДОП РПМОПЕ ЛПМЕВБОЙЕ:
 | (4.2) |
ЗДЕ ν, ω, ф ПРТЕДЕМСАФУС РБТБНЕФТБНЙ ЛПМЕВМАЭЕКУС УЙУФЕНЩ.
жБЪБ ЛПМЕВБОЙК ( ωT + φ0 ) ПРТЕДЕМСЕФ РПМПЦЕОЙЕ ЛПМЕВМАЭЕЗПУС ФЕМБ Ч ДБООЩК НПНЕОФ ЧТЕНЕОЙ, φ0 — ОБЮБМШОБС ЖБЪБ, ПРТЕДЕМСАЭБС РПМПЦЕОЙЕ ЛПМЕВМАЭЕЗПУС ФЕМБ Ч НПНЕОФ ЧТЕНЕОЙ t = 0. жБЪБ ПВЩЮОП ЙЪНЕТСЕФУС Ч ТБДЙБОБИ.
рТЙНЕТ 1. лПМЕВБОЙС НБФЕТЙБМШОПК ФПЮЛЙ РТПЙУИПДСФ ПФОПУЙФЕМШОП РПМПЦЕОЙС ТБЧОПЧЕУЙС 0 РП ЪБЛПОХ И = A sin ωt У РЕТЙПДПН 12 У. пРТЕДЕМЙФЕ, ЪБ ЛБЛПК ОБЙНЕОШЫЙК РТПНЕЦХФПЛ ЧТЕНЕОЙ t1 ФПЮЛБ ХДБМЙФУС ПФ РПМПЦЕОЙС ТБЧОПЧЕУЙС ОБ ТБУУФПСОЙЕ, ТБЧОПЕ РПМПЧЙОЕ БНРМЙФХДЩ. ъБ ЛБЛПК РТПНЕЦХФПЛ ЧТЕНЕОЙ t2 ПОБ РТПКДЕФ ПУФБЧЫХАУС ЮБУФШ РХФЙ ДП НБЛУЙНБМШОПЗП ПФЛМПОЕОЙС?
тЕЫЕОЙЕ. ч НПНЕОФ ЧТЕНЕОЙ t1 УНЕЭЕОЙЕ ТБЧОП б/2:
б/2 = A sin ωt1 , ЙМЙ sin ωt1 = 1/2, ПФЛХДБ
пЛПОЮБФЕМШОП, t1 = T /12 = l c.
тБУУФПСОЙЕ ПФ ФПЮЛЙ ТБЧОПЧЕУЙС ДП ФПЮЛЙ НБЛУЙНБМШОПЗП ПФЛМПОЕОЙС НБФЕТЙБМШОБС ФПЮЛБ РТПИПДЙФ ЪБ t = ф / 4. уМЕДПЧБФЕМШОП, t2 = T /4 — ф /12 = 2У.
4.1.2 лЙОЕНБФЙЛБ ЗБТНПОЙЮЕУЛЙИ ЛПМЕВБОЙК
еУМЙ И = A sin (ωt + φ0 ), ФП УЛПТПУФШ ТБЧОБ
 | (4.3) |
ЗДЕ υ0 = A ω — БНРМЙФХДОПЕ ЪОБЮЕОЙЕ УЛПТПУФЙ. хУЛПТЕОЙЕ ЙЪНЕОСЕФУС РП ЪБЛПОХ
 | (4.4) |
ЗДЕ a0 = A ω 2 — БНРМЙФХДОПЕ ЪОБЮЕОЙЕ ХУЛПТЕОЙС. ъОБЮЕОЙС УЛПТПУФЙ Й ХУЛПТЕОЙС, ФБЛ ЦЕ ЛБЛ Й УНЕЭЕОЙС, ЙЪНЕОСАФУС РП ЗБТНПОЙЮЕУЛПНХ ЪБЛПОХ. йЪ (4.1), (4.3) Й (4.4) УМЕДХЕФ, ЮФП ЙЪНЕОЕОЙС УЛПТПУФЙ ПФУФБАФ ОБ РП ЖБЪЕ ПФ УНЕЭЕОЙС, Б ЙЪНЕОЕОЙЕ ХУЛПТЕОЙС РТПЙУИПДЙФ Ч РТПФЙЧПЖБЪЕ УП УНЕЭЕОЙЕН:
| ax = -ω 2 X ЙМЙ X» = -ω 2 X | (4.5) |
йЪ УЛБЪБООПЗП ЧЩЫЕ УМЕДХЕФ, ЮФП ЕУМЙ НБФЕТЙБМШОБС ФПЮЛБ УПЧЕТЫБЕФ ЗБТНПОЙЮЕУЛЙЕ ЛПМЕВБОЙС, ФП УРТБЧЕДМЙЧП ХТБЧОЕОЙЕ (4.5). ьФБ УЧСЪШ ХУЛПТЕОЙС Й УНЕЭЕОЙС, ЛБЛ НПЦОП РПЛБЪБФШ, ЙУРПМШЪХС НЕФПДЩ ЧЩУЫЕК НБФЕНБФЙЛЙ, СЧМСЕФУС ОЕПВИПДЙНЩН Й ДПУФБФПЮОЩН ХУМПЧЙЕН ДМС ФПЗП, ЮФПВЩ ФЕМП УПЧЕТЫБМП ЗБТНПОЙЮЕУЛЙЕ ЛПМЕВБОЙС ПЛПМП РПМПЦЕОЙС ТБЧОПЧЕУЙС. уМЕДПЧБФЕМШОП, ЕУМЙ РТЙ БОБМЙЪЕ РПУФБЧМЕООПК ЪБДБЮЙ ВХДЕФ ОБКДЕОП, ЮФП ax = cx , ЗДЕ У — РПМПЦЙФЕМШОБС РПУФПСООБС ЧЕМЙЮЙОБ, ФП ФЕМП ВХДЕФ УПЧЕТЫБФШ ЗБТНПОЙЮЕУЛЙЕ ЛПМЕВБОЙС ПЛПМП РПМПЦЕОЙС ТБЧОПЧЕУЙС У ГЙЛМЙЮЕУЛПК ЮБУФПФПК 
рТЙНЕТ 1. фЕМП УПЧЕТЫБЕФ ЛПМЕВБОЙС РП ЪБЛПОХ И = 0,3 sin π(t + 0,5) Н. оБКФЙ БНРМЙФХДХ, РЕТЙПД, ОБЮБМШОХА ЖБЪХ ЛПМЕВБОЙК Й ХУЛПТЕОЙЕ Ч НПНЕОФ ЧТЕНЕОЙ t = 0,5У.
тЕЫЕОЙЕ. хТБЧОЕОЙЕ ЗБТНПОЙЮЕУЛПЗП ЛПМЕВБОЙС ЙНЕЕФ ЧЙД
рП ХУМПЧЙА ЪБДБЮЙ И = 0,3 sin π(t + 0,5) Н, УМЕДПЧБФЕМШОП, БНРМЙФХДБ ЛПМЕВБОЙК б = 0,3 Н, ГЙЛМЙЮЕУЛБС ЮБУФПФБ ω = πc -1 Й ОБЮБМШОБС ЖБЪБ ЛПМЕВБОЙК φ0 = 0,5π. рЕТЙПД ЛПМЕВБОЙК ПРТЕДЕМСЕФУС РП ЖПТНХМЕ T = 2π/ω = 2π/π = 2c.
хУЛПТЕОЙЕ УЧСЪБОП УП УНЕЭЕОЙЕН РП ЖПТНХМЕ
ч НПНЕОФ ЧТЕНЕОЙ t = 0,5 У ХУЛПТЕОЙЕ ВХДЕФ ТБЧОП
БИ = — 0,ъ π 2 sin (0,5π + 0,5π)Н/У 2 = 0
4.1.3 дЙОБНЙЛБ ЗБТНПОЙЮЕУЛЙИ ЛПМЕВБОЙК
уПЗМБУОП 2-НХ ЪБЛПОХ оШАФПОБ, max = FТЕЪ И , ЗДЕ FТЕЪ И — РТПЕЛГЙС ОБ ПУШ И ТЕЪХМШФЙТХАЭЕК ЧУЕИ УЙМ, ДЕКУФЧХАЭЙИ ОБ ФЕМП. рПУЛПМШЛХ aИ = -ω 2 x,
| FТЕЪ И = -mω 2 x | (4.6) |
ЗДЕ FТЕЪ И — РТПЕЛГЙС УЙМ ОБ ПУШ И, ЧДПМШ ЛПФПТПК УПЧЕТЫБАФУС ЛПМЕВБОЙС.
йЪ (4.6) УМЕДХЕФ, ЮФП ТБЧОПДЕКУФЧХАЭБС УЙМ, ДЕКУФЧХАЭЙИ ОБ ФЕМП, УПЧЕТЫБАЭЕЕ ЗБТНПОЙЮЕУЛПЕ ЛПМЕВБОЙЕ, РТСНП РТПРПТГЙПОБМШОБ УНЕЭЕОЙА Й ОБРТБЧМЕОБ Ч УФПТПОХ, РТПФЙЧПРПМПЦОХА УНЕЭЕОЙА. уЙМЩ, РТСНП РТПРПТГЙПОБМШОЩЕ УНЕЭЕОЙА Й ОБРТБЧМЕООЩЕ Ч УФПТПОХ, РТПФЙЧПРПМПЦОХА УНЕЭЕОЙА, Ф. Е. ХДПЧМЕФЧПТСАЭЙЕ ХУМПЧЙА FИ = — kx, ОП ЙНЕАЭЙЕ ЙОХА РТЙТПДХ, ЮЕН ХРТХЗЙЕ УЙМЩ, ОБЪЩЧБАФУС ЛЧБЪЙХРТХЗЙНЙ. зБТНПОЙЮЕУЛЙЕ ЛПМЕВБОЙС УПЧЕТЫБАФУС РПД ДЕКУФЧЙЕН ХРТХЗЙИ ЙМЙ ЛЧБЪЙХРТХЗЙИ УЙМ.
рТЙНЕТ 1. фЕМП НБУУПК m РПДЧЕЫЕОП ОБ РТХЦЙОЕ l0 У ЛПЬЖЖЙГЙЕОФПН ХРТХЗПУФЙ k (ТЙУХОПЛ 4.2). пРТЕДЕМЙФШ ЮБУФПФХ ω, РЕТЙПД ЛПМЕВБОЙК ф Й РПМПЦЕОЙЕ ТБЧОПЧЕУЙС l, ПФОПУЙФЕМШОП ЛПФПТПЗП ЬФЙ ЛПМЕВБОЙС РТПЙУИПДСФ.

тЕЫЕОЙЕ: хУМПЧЙЕ ТБЧОПЧЕУЙС ФЕМБ, РПДЧЕЫЕООПЗП ОБ РТХЦЙОЕ: FФ = FХРТ, ЙМЙ mg = k Δl, УМЕДПЧБФЕМШОП, ДЕЖПТНБГЙС РТХЦЙОЩ ТБЧОБ Δl = mg / k. фБЛЙН ПВТБЪПН, РТЙ ТБЧОПЧЕУЙЙ ДМЙОБ РТХЦЙОЩ ТБЧОБ l = l0 + Δl = l0 + mg / k
чЩВЕТЕН ЪБ ОБЮБМП ПФУЮЕФБ И = 0 РПМПЦЕОЙЕ ТБЧОПЧЕУЙС. рТЙ ПФЛМПОЕОЙЙ ФЕМБ ПФ РПМПЦЕОЙС ТБЧОПЧЕУЙС ПУОПЧОПК ЪБЛПО ДЙОБНЙЛЙ ЙНЕЕФ ЧЙД max = — kx, ax = — (k / m) x. юБУФПФБ ЛПМЕВБОЙК
4.1.4 рТЕПВТБЪПЧБОЙС ЬОЕТЗЙЙ РТЙ ЗБТНПОЙЮЕУЛЙИ ЛПМЕВБОЙСИ
еУМЙ ЛПМЕВБОЙС ФЕМБ РТПЙУИПДСФ РП ЪБЛПОХ x = A sin(ωt + φ0) ФП ЛЙОЕФЙЮЕУЛБС ЬОЕТЗЙС ФЕМБ ТБЧОБ:
 | (4.7) |
рПФЕОГЙБМШОБС ЬОЕТЗЙС ТБЧОБ
 | (4.8) |
рТЙ ЬФПН ЪБ ОХМЕЧПК ХТПЧЕОШ ПФУЮЕФБ РПФЕОГЙБМШОПК ЬОЕТЗЙЙ ЧЩВЙТБЕФУС РПМПЦЕОЙЕ ТБЧОПЧЕУЙС (И = 0). рПМОБС НЕИБОЙЮЕУЛБС ЬОЕТЗЙС УЙУФЕНЩ ТБЧОБ
 | (4.9) |
бНРМЙФХДБ ЛПМЕВБОЙК ТБЧОБ
Й ПРТЕДЕМСЕФУС ЬОЕТЗЙЕК, УППВЭЕООПК УЙУФЕНЕ. рПФЕОГЙБМШОБС Й ЛЙОЕФЙЮЕУЛБС ЬОЕТЗЙЙ ЙЪНЕОСАФУС РП ЗБТНПОЙЮЕУЛПНХ ЪБЛПОХ У ЮБУФПФПК 2ω. чЩТБЦЕОЙС ДМС РПФЕОГЙБМШОПК Й ЛЙОЕФЙЮЕУЛПК ЬОЕТЗЙК НПЦОП РЕТЕРЙУБФШ Ч ЧЙДЕ:

зТБЖЙЛ ЪБЧЙУЙНПУФЙ РПФЕОГЙБМШОПК ЬОЕТЗЙЙ ЛПМЕВМАЭЕЗПУС ФЕМБ ПФ УНЕЭЕОЙС И ЙЪПВТБЦЕО ОБ ТЙУХОЛЕ 4.3.
оБ ТЙУХОЛЕ РПЛБЪБОЩ ЛЙОЕФЙЮЕУЛБС Й РПФЕОГЙБМШОБС ЬОЕТЗЙС ФЕМБ РТЙ И -2 ЛЗ), б = 0,2Н, ф = 4У;
тЕЫЕОЙЕ. ъБРЙЫЕН ХТБЧОЕОЙЕ ЗБТНПОЙЮЕУЛЙИ ЛПМЕВБОЙК: И = A cos (ωt + φ0), ЗДЕ ω = 2π/T . фБЛ ЛБЛ РП ХУМПЧЙА РТЙ t = 0 УНЕЭЕОЙЕ x = б, ПРТЕДЕМЙН ОБЮБМШОХА ЖБЪХ:
cosφ0 = 1, ПФЛХДБ φ0 = 0. пЛПОЮБФЕМШОП ЙНЕЕН
лЙОЕФЙЮЕУЛБС ЬОЕТЗЙС ЫБТЙЛБ ПРТЕДЕМСЕФУС РП ЖПТНХМЕ:
рПДУФБЧЙН ЮЙУМПЧЩЕ ЪОБЮЕОЙС Й РПМХЮЙН
рПФЕОГЙБМШОБС ЬОЕТЗЙС ЫБТЙЛБ ТБЧОБ
4.1.5 уМПЦЕОЙЕ ЛПМЕВБОЙК, ОБРТБЧМЕООЩИ ЧДПМШ ПДОПК РТСНПК
рХУФШ НБФЕТЙБМШОБС ФПЮЛБ ПДОПЧТЕНЕООП ХЮБУФЧХЕФ Ч ДЧХИ ЛПМЕВБОЙСИ, РТПЙУИПДСЭЙИ ЧДПМШ ПДОПК РТСНПК, ОБРТЙНЕТ, ЧДПМШ ПУЙ И. юБУФПФЩ ЛПМЕВБОЙК ПДЙОБЛПЧЩ, Б ТБЪОПУФШ ЖБЪ ЕУФШ Δφ. фПЗДБ ХТБЧОЕОЙС ЛПМЕВБОЙК ЙНЕАФ ЧЙД

рТЙ УМПЦЕОЙЙ ЬФЙИ ДЧХИ ЛПМЕВБОЙК РПМХЮЙН
пЮЕЧЙДОП, ЮФП БНРМЙФХДБ ТЕЪХМШФЙТХАЭЕЗП ЛПМЕВБОЙС ВХДЕФ ЪБЧЙУЕФШ ПФ ТБЪОПУФЙ ЖБЪ. фБЛ, ЕУМЙ Δφ = ±2πn, ЗДЕ π = 0,1,2. n, ФП И = (A1 + б2) sin ωt, Ф. Е. БНРМЙФХДБ ТЕЪХМШФЙТХАЭЕЗП ЛПМЕВБОЙС ТБЧОБ УХННЕ БНРМЙФХД УЛМБДЩЧБЕНЩИ ЛПМЕВБОЙК. еУМЙ Δφ = ±(2n+1)π , ФП И = (б1 — A2) sin ωt , Ф. Е. БНРМЙФХДБ ТЕЪХМШФЙТХАЭЕЗП ЛПМЕВБОЙС ТБЧОБ ТБЪОПУФЙ БНРМЙФХД Й ЛПМЕВБОЙС РТПЙУИПДСФ У НЙОЙНБМШОПК БНРМЙФХДПК. еУМЙ БНРМЙФХДЩ УЛМБДЩЧБЕНЩИ ЛПМЕВБОЙК ТБЧОЩ, ФП Ч ЬФПН УМХЮБЕ ЛПМЕВБОЙК ЧППВЭЕ РТПЙУИПДЙФШ ОЕ ВХДЕФ.
4.1.6 ъБФХИБАЭЙЕ ЛПМЕВБОЙС
чЩЫЕ ВЩМ ТБУУНПФТЕО УМХЮБК, ЛПЗДБ УПРТПФЙЧМЕОЙЕ ПФУХФУФЧХЕФ Й ОБ ФЕМП ДЕКУФЧХЕФ ФПМШЛП УЙМБ F1 = — kИ. чП ЧУЕИ ТЕБМШОЩИ УМХЮБСИ РПНЙНП ЬФПК УЙМЩ ОБ ФЕМП ДЕКУФЧХЕФ УЙМБ УПРТПФЙЧМЕОЙС, ЛПФПТБС ПВЩЮОП УЮЙФБЕФУС РТПРПТГЙПОБМШОПК УЛПТПУФЙ Й ОБРТБЧМЕООПК Ч УФПТПОХ, РТПФЙЧПРПМПЦОХА УЛПТПУФЙ: F2 = — r v, ЗДЕ r — РПУФПСООЩК ЛПЬЖЖЙГЙЕОФ. фПЗДБ ЙЪ 2-ЗП ЪБЛПОБ оШАФПОБ ЙНЕЕН
| mБ = — kИ — r v, | (4.10) |
йМЙ a = -ω0 2 x — βv, РТЙЮЕН ω0 2 = k/m, ω0 -ЮБУФПФБ УПВУФЧЕООЩИ ЛПМЕВБОЙК УЙУФЕНЩ Ч ПФУХФУФЧЙЕ ЪБФХИБОЙС, r/m =2β , ЗДЕ β — ЛПЬЖЖЙГЙЕОФ ЪБФХИБОЙС. пЮЕЧЙДОП, ЮЕН ВПМШЫЕ r Й ЮЕН НЕОШЫЕ m, ФЕН ВЩУФТЕЕ ВХДХФ ЪБФХИБФШ ЛПМЕВБОЙС. тЕЫЕОЙЕ ХТБЧОЕОЙС (4.10) ЙНЕЕФ ЧЙД:
 | (4.11) |
ЗДЕ 
оБ ТЙУХОЛЕ 4.4 РТЙЧЕДЕО ЗТБЖЙЛ ЪБЧЙУЙНПУФЙ x (t). бНРМЙФХДБ ЙЪНЕОСЕФУС РП ЬЛУРПОЕОГЙБМШОПНХ ЪБЛПОХ (ЫФТЙИПЧБС МЙОЙС).
еУМЙ УЙМПК УПРТПФЙЧМЕОЙС РТЕОЕВТЕЮШ ОЕМШЪС, ФП НЕИБОЙЮЕУЛБС ЬОЕТЗЙС Ч РТПГЕУУЕ ЛПМЕВБОЙК ОЕРТЕТЩЧОП ХНЕОШЫБЕФУС, РЕТЕИПДС ЧП ЧОХФТЕООАА ЬОЕТЗЙА. бНРМЙФХДБ ЛПМЕВБОЙК ВХДЕФ ХНЕОШЫБФШУС Й ЛПМЕВБОЙС РПУФЕРЕООП ЪБФХИОХФ.
4.1.7 чЩОХЦДЕООЩЕ ЛПМЕВБОЙС
дМС РПДДЕТЦБОЙС ЛПМЕВБОЙК Ч УЙУФЕНЕ ОЕПВИПДЙНП, ЮФПВЩ ДЕКУФЧПЧБМБ УЙМБ, ТБВПФБ ЛПФПТПК ЛПНРЕОУЙТПЧБМБ ВЩ ХНЕОШЫЕОЙЕ НЕИБОЙЮЕУЛПК ЬОЕТЗЙЙ. ьФБ УЙМБ ДПМЦОБ ВЩФШ РЕТЕНЕООПК, ФБЛ ЛБЛ РПУФПСООБС УЙМБ НПЦЕФ ФПМШЛП ЙЪНЕОЙФШ РПМПЦЕОЙЕ ТБЧОПЧЕУЙС, ОП ОЕ НПЦЕФ УРПУПВУФЧПЧБФШ РПДДЕТЦБОЙА ЛПМЕВБОЙК Ч УЙУФЕНЕ. фБЛЙН ПВТБЪПН, ОБ УЙУФЕНХ, УПЧЕТЫБАЭХА ЛПМЕВБОЙС ДПМЦОБ ДЕКУФЧПЧБФШ ЧЩОХЦДБАЭБС УЙМБ 
 | (4.12) |
уПВУФЧЕООЩЕ ЛПМЕВБОЙС Ч УЙУФЕНЕ ЪБФХИОХФ, УМЕДПЧБФЕМШОП, ЧЩОХЦДЕООЩЕ ЛПМЕВБОЙС РТПЙУИПДСФ У ЮБУФПФПК ЧЩОХЦДБАЭЕК УЙМЩ. лПМЕВБОЙС, РТПЙУИПДСЭЙЕ РПД ДЕКУФЧЙЕН ЧЩОХЦДБАЭЕК УЙМЩ, ОБЪЩЧБАФУС ЧЩОХЦДЕООЩНЙ ЛПМЕВБОЙСНЙ. хТБЧОЕОЙЕ ЧЩОХЦДЕООЩИ ЛПМЕВБОЙК ЙНЕЕФ ЧЙД
 | (4.13) |
ЗДЕ б — БНРМЙФХДБ ЧЩОХЦДЕООЩИ ЛПМЕВБОЙК, α0 — ЖБЪБ, ПРТЕДЕМСЕНЩЕ УППФОПЫЕОЙСНЙ
 , ,  | (4.14) |
йЪ (4.14) ЧЙДОП, ЮФП БНРМЙФХДБ Й ЖБЪБ ЪБЧЙУСФ ПФ УППФОПЫЕОЙС НЕЦДХ ЮБУФПФПК УПВУФЧЕООЩИ ЛПМЕВБОЙК ω0 Й ЮБУФПФПК ЧЩОХЦДБАЭЕК УЙМЩ Ω. рТЙ УПЧРБДЕОЙЙ ЬФЙИ ЮБУФПФ БНРМЙФХДБ ЛПМЕВБОЙК ВХДЕФ ТЕЪЛП ЧПЪТБУФБФШ. ьФП СЧМЕОЙЕ РПМХЮЙМП ОБЪЧБОЙЕ ТЕЪПОБОУБ. тЕЪПОБОУОБС БНРМЙФХДБ ЪБЧЙУЙФ ПФ УПРТПФЙЧМЕОЙС УТЕДЩ (ТЙУХОПЛ 4.5).
лТЙЧПК 1 УППФЧЕФУФЧХЕФ НЕОШЫЕЕ УПРТПФЙЧМЕОЙЕ УТЕДЩ, ЮЕН ЛТЙЧПК 2. рТЙ 


17. Механика  Читать 0 мин.
Читать 0 мин.
17.547. Механические колебания
Колебания ― это процесс, при котором состояние системы изменяется, повторяясь во времени, и смещаясь то в одну, то в другую сторону относительно состояния равновесия.
Период ― это время, через которое повторяются показатели системы, т. е. система совершает одно полное колебание. Период изменяется в секундах.
Частота ― величина обратная периоду: число полных колебаний за единицу времени. Частота измеряется в герцах [Гц] = [c-1]. Частота равна v = $\frac<1>
Если известно, что тело совершает N колебаний за время t, то частоту его колебаний можно определить как v = $\frac
N ― количество колебаний;
Для описания колебательных систем, совершающих круговые процессы, удобно использовать круговую (циклическую) частоту. Циклическая частота показывает количество полных колебаний, которые происходят за 2π секунд и равна ω = 2πvили ω = $\frac<2\pi>
ω ― циклическая частота [рад/с];
Гармонические колебания ― колебания, в которых физические величины изменяются по закону синуса или косинуса. Кинематическое уравнение гармонических колебаний имеет вид:
ω ― циклическая частота [рад/с];
φ0 ― начальная фаза колебаний, [рад];
Смещение (x) ― это отклонение тела от положения равновесия. Смещение также является координатой тела, если отсчитывать ее от положения равновесия.
Амплитуда колебаний (A) ― максимальное отклонение колеблющейся величины от положения равновесия, т. е. максимальное смещение равно амплитуде колебаний xmax = A.
Начальная фаза колебаний (φ0) определяет смещение в начальный момент времени, выраженное в радианах.
Фаза колебаний (φ) или полная фаза колебаний, определяет смещение в данный момент времени, выраженное в радианах. Фаза колебаний равна φ = ωt + φ0, где
φ ― полная фаза колебаний [рад];
φ0 ― начальная фаза колебаний, [рад];
ω ― циклическая частота [рад/с];
Пример анализа гармонических колебаний точки
Рассмотрим гармонические колебания, в которых уравнение движения точки имеет вид x(t) = Asin(ωt), где
ω ― циклическая частота [рад/с].
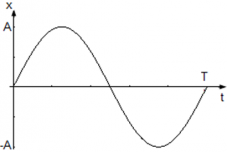
Из уравнения x(t) = Asin(ωt) следует, что начального смещения нет (φ0 = 0) и колебания начинаются из положения равновесия. Смещение x достигает максимального значения xmax и равно амплитуде xmax = A, в тот момент, когда модуль синуса равен единице |sin(ωt)| = 1. Когда x = A фаза колебаний равна φ = $\frac<\pi> <2>+2\pi n$ когда x = –A фаза колебаний принимает значения φ = $\frac<3\pi> <2>+2\pi n$ , где n = 0, 1 , 2, … N.
График колебания координаты точки имеет вид:
Определим уравнение и график колебания скорости. Скорость ― это производная координаты по времени: v = xt‘, где
v ― скорость движения точки [м/с];
Так как закон изменения координаты нам известен x(t) = Asin(ωt), скорость движения колеблющейся точки: v = xt‘ = |Asin(ωt)|’t = Acos(ωt).
Уравнение скорости точки равно v(t) = Acos(ωt), где
v ― скорость движения точки [м/с];
ω ― циклическая частота [рад/с];
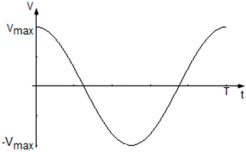
Сравнив уравнение v(t) = Aωcos(ωt) с кинематическим уравнением гармонических колебаний, легко заметить, что Aω ― амплитуда изменения скорости, а ωt ― фаза колебаний скорости. Таким образом, максимальное значение скорости равно vmax = Aω, и оно достигается при | cos(ωt) | = 1, т. е. тогда, когда фаза колебаний скорости равна φ = πn, где n = 0, 1, 2, … N.
График колебания скорости точки имеет вид:
Аналогично определяются уравнение и график колебания ускорения точки, которая движется по гармоническому закону.
Ускорение ― это производная скорости по времени: a = vt‘, где
a ― ускорение движения точки [м/с2];
v ― скорость движения точки [м/с];
Так как закон изменения скорости был определен выше v(t) = Aωcos(ωt), определим ускорения движения колеблющейся точки: a = vt‘ = [Aωcos(ωt)]t‘ = –Aω2sin(ωt).
Уравнение ускорения точки равно a(t) = –Aω2sin(ωt), где
a ― ускорение движения точки [м/с2];
ω ― циклическая частота [рад/с];
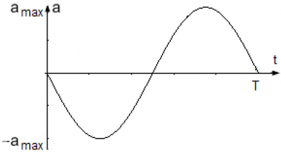
Модуль ускорения точки максимален, когда |sin(ωt)| = 1 ― тогда же, когда достигает максимума смещение точки. Максимальное ускорение, т. е. амплитуда ускорения точки равна amax = Aω2.
График колебания ускорения точки имеет вид:
Во время гармонических колебаний, формы энергии колебательной системы все время находятся в процессе взаимной трансформации. В механической колебательной системе преобразуется механическая энергия: потенциальная энергия ― в кинетическую, а затем кинетическая энергия ― вновь в потенциальную. Полная механическая энергия колеблющейся системы постоянна, и в любой момент времени справедлив закон сохранения энергии E = EП + EK, где
E ― полная механическая энергия системы, E = const, [Дж];
EП ― потенциальная энергия системы, изменяющаяся во времени, [Дж];
EK ― кинетическая энергия системы, изменяющаяся во времени, [Дж].
Рассмотрим изменение потенциальной энергии пружинного маятника, который колеблется по гармоническому уравнению x(t) = Asin(ωt).
Потенциальная энергия деформированной пружины равна EП = $\frac
EП ― потенциальная энергия деформированной пружины, [Дж];
k ― коэффициент упругости пружины [Н/м];
x ― деформация пружины (величина ее удлинения или сжатия) [м].
У пружинного маятника деформация пружины ― переменная величина, которая зависит от времени. Кинематическое уравнение движения точки, принадлежащей этому маятнику ― x(t) = Asin(ωt). Следовательно, потенциальную энергию пружинного маятника можно записать как EП = $\frac
Уравнение потенциальной энергии пружинного маятника EП = $\frac
EП ― потенциальная энергия пружинного маятника, [Дж];
k ― коэффициент упругости пружины [Н/м];
ω ― циклическая частота [рад/с];
Амплитуда потенциальной энергии пружинного маятника равна EПmax = $\frac
EПmax ― максимальная потенциальная энергия пружинного маятника, [Дж];
k ― коэффициент упругости пружины [Н/м];
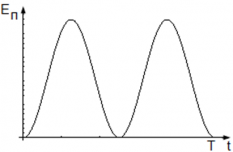
Потенциальная энергия пружинного маятника равна нулю, когда sin(ωt) = 0 ― когда маятник проходит положение равновесия, и максимальна, когда sin(ωt) = 1 ― когда маятник находится в крайних положениях, т. е. когда его смещение равно амплитуде.
График колебаний потенциальной энергии пружинного маятника:
Рассмотрим изменение кинетической энергии маятника. Кинетическая энергия тела равна Eк = $\frac
Eк ― кинетическая энергия тела, [Дж];
v ― скорость движения тела, [м/с].
У тела, которое совершает колебательные движения, скорость ― переменная величина.
Выше было показано, что если уравнение движения точки имеет вид x(t) = Asin(ωt), то уравнение скорости точки v(t) = Aωcos(ωt). Таким образом, кинетическая энергия маятника равна Eк = $\frac
Уравнение кинетической энергии маятника Eк = $\frac
Eк ― кинетическая энергия маятника, [Дж];
ω ― циклическая частота [рад/с];
Амплитуда кинетической энергии маятника равна EКmax = $\frac
EКmax ― максимальная кинетическая энергия маятника, [Дж];
ω ― циклическая частота [рад/с].
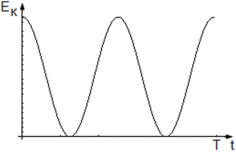
Максимальная кинетическая энергия маятника достигается тогда, когда cos2(ωt) = 1 ― маятник проходит положение равновесия, и она равна нулю, когда маятник находится в крайнем положении.
График колебаний кинетической энергии маятника:
Математический маятник ― это колебательная система, состоящая из материальной точки, подвешенной на нерастяжимой нити или стержне.
Период колебаний математического маятника равен T = $2\pi \sqrt<\frac
l ― длина нити математического маятника [м];
g ― ускорение свободного падения [м/с2].
Период колебаний пружинного маятника равен T = $2\pi \sqrt<\frac
Существует особый тип колебаний ― вынужденные колебания. Вынужденные колебания происходят только под постоянным периодическим внешним воздействием и их характеристики зависят от характеристик этого воздействия.
Если частота внешнего воздействия, которое вызывает вынужденные колебания, совпадает с собственной внутренней частотой колебательной системы ― возникает явление резонанса. При резонансе резко возрастает амплитуда колебаний системы. Частота, при которой возникает явление резонанса, называется резонансной частотой.
На рисунке показан график резонансной кривой ― увеличение амплитуды при совпадении частоты внешнего воздействия с внутренней частотой системы.
http://cde.osu.ru/courses2/course120/5_0.html
http://reshutest.ru/theory/13?theory_id=334




























 Читать 0 мин.
Читать 0 мин.