Движение тела с переменной массой. Уравнение Мещерского. Формула Циолковского
Вы будете перенаправлены на Автор24
Уравнение движения тела с переменной массой
Под переменной массой будем понимать массу тел, которая при медленном движении тел меняется за счет потери или приобретения вещества.
Выведем уравнение движения материальной точки с переменной массой на примере движения ракеты. Принцип действия ракеты очень прост. Ракета с большой скоростью выбрасывает вещество (газы), воздействуя на него с большой силой. Выбрасываемое вещество с той же, но противоположно направленной силой в свою очередь действует на ракету и сообщает ей ускорение в противоположном направлении. На ракету действуют внешние силы: сила земной тяжести, гравитационное притяжение Солнца и планет, а также сила сопротивления среды, в которой движется ракета.
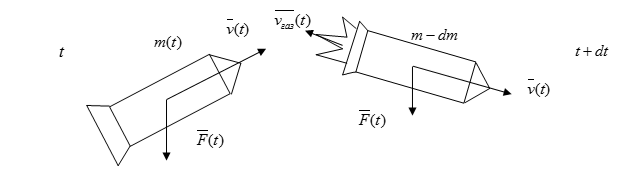
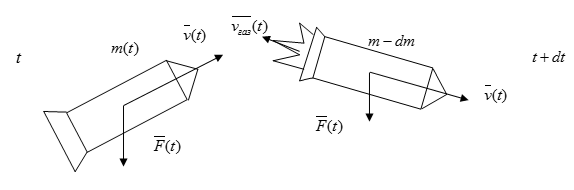
Пусть $m(t)$- масса ракеты в произвольный момент времени $t$, а $v(t)$- ее скорость в тот же момент. Количество движения ракеты в этот момент времени будет $mv$. Спустя время $dt$ масса и скорость ракеты получат приращение $dm$ и $dv$ (величина $dm$ отрицательна). Количество движения ракеты станет равным $(m+dm)(v+dv)$. Сюда надо добавить количество движения газов, образовавшихся за время $dt$. Оно равно $dm_ <газ>v_ <газ>$, где $dm_ <газ>$- масса газов, образовавшихся за время $dt$, а $v_ <газ>$- их скорость. Вычитая из суммарного количества движения в момент $t+dt$ количество движения системы в момент времени $t$, найдем приращение этой величины за время $dt$. Это приращение равно $Fdt$, где $F$- геометрическая сумма всех внешних сил, действующих на ракету. Таким образом:
Время $dt$ и приращения $dm$ и $dv$ устремим к нулю, т.к. нас интересуют предельные отношения или производные $dm/dt$ и $dv/dt$. Поэтому, раскрывая скобки, можно отбросить произведение $dm\cdot dv$, как бесконечно малую высшего порядка. Далее, ввиду сохранения массы, $dm+dm_ <газ>=0$. Пользуясь этим, можно исключить массу газов $dm_ <газ>$. А разность $v_ <отн>=v_ <газ>-v$ есть скорость истечения газов относительно ракеты — скорость газовой струи. С учетом этих замечаний уравнение (1) преобразуется к виду:
Готовые работы на аналогичную тему
Разделив на $dt$, получаем:
Уравнение Мещерского
По форме уравнение (3) совпадает с уравнением, выражающим второй закон Ньютона. Однако масса тела $m$здесь не постоянна, а меняется во времени из-за потери вещества. К внешней силе $F$ добавляется дополнительный член $v_ <отн>\frac
Формула Циолковского
Применим уравнение (2) к движению ракеты, на которую не действуют никакие внешние силы. Полагая $F=0$, получим:
Допустим, что ракета движется прямолинейно в направлении, противоположном скорости газовой струи $v_ <отн>$. Если направление полета принять за положительное, то проекция вектора $v_ <отн>$ на это направление будет отрицательной и равной $-v_ <отн>$. Поэтому в скалярной форме предыдущее уравнение можно записать так $mdv=v_ <отн>dm$. Тогда:
Скорость газовой струи $v_ <отн>$ может меняться во время полета. Однако простейшим и наиболее важным является случай, когда она постоянна. Предположение о постоянстве сильно облегчает решение уравнения (4). В этом случае:
Значение постоянной интегрирования С определяется начальными условиями. Допустим, что в начальный момент времени скорость ракеты равна нулю, а ее масса равна $m_ <0>$. Тогда из предыдущего уравнения получаем:
Последнее соотношение называется формулой Циолковского.
Формула Циолковского позволяет рассчитать запас топлива, необходимый, чтобы сообщить ракете скорость $\upsilon $.
Величина достигаемой ракетой максимальной скорости не зависит от времени сгорания топлива.
Оптимальным путем изменения достигаемой максимальной скорости является увеличение относительной скорости истечения газов.
Для получения первой космической скорости при меньшем соотношении между массой ракеты и требуемой массы топлива целесообразно использование многоступенчатых ракет.
Примеры
Космический корабль двигался с постоянной по величине скоростью $v$. Для изменения направления его полета включается двигатель, выбрасывающий струю газа со скоростью $v_ <отн>$ относительно корабля в направлении, перпендикулярном к его траектории. Определить угол $\alpha $, на который повернется вектор скорости корабля, если начальная масса его $m_ <0>$, а конечная $m$.
Решение:
Ускорение корабля по абсолютной величине равно:
$a=\omega ^ <2>r=\omega v$, причем $v=const$. Поэтому уравнение движения:
$m\frac
Так как $d\alpha =\omega dt$ есть угол поворота за время $dt$, интегрируя наше уравнение, получим:
Ответ: угол поворота вектора скорости равен: $\alpha =\frac
Ракета перед стартом имеет массу $m_ <0>=250$кг. На какой высоте окажется ракета через $t=20$с после начала работы двигателей? Расход топлива равен $\mu =4$кг/с и скорость истечения газов относительно ракеты $v_ <отн>$$=1500$м/с постоянны. Поле тяготения Земли считать однородным.
Дано: $m_ <0>=250$кг, $t=20$с, $\mu =4$кг/с, $v_<отн>=1500$м/с.
Решение:
Запишем уравнение Мещерского в однородном поле тяготения Земли в виде:
где $m=m_ <0>-\mu t$, а $v_ <0>$- скорость ракеты в момент времени $t$. Разделяя переменные получаем:
Решение данного уравнения, удовлетворяющего начальному условию $v_ <0>=0$ при $t=0$, имеет вид:
Учитывая что $H_ <0>=0$ при $t=0$ получим:
Подставляя начальные значения, получаем:
Ответ: через $20$с ракета окажется на высоте $H=3177,5$м.
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 06 04 2021
Движение тела с переменной массой
Для начала сформулируем, что такое переменная масса.
Переменная масса – это масса тела, которая может меняться при медленных движениях из-за частичных приобретений или потерь составляющего вещества.
Уравнение движения материальной точки с переменной массой
Чтобы записать уравнение движения для тела с такой массой, возьмем для примера движение ракеты. В основе ее перемещений лежит очень простой принцип: она движется за счет выброса вещества с большой скоростью, а также сильного воздействия, оказываемого на это вещество. В свою очередь выбрасываемые газы также оказывают воздействие на ракету, придавая ей ускорение в противоположном направлении. Кроме того, ракета находится под действием внешних сил, таких, как гравитация Солнца и других планет, земная тяжесть, сопротивление среды, в которой она совершает движение.
Обозначим массу ракеты в какой-либо момент времени t как m ( t ) , а ее скорость как v ( t ) . То количество движения, которая она при этом совершает, будет равно m v . После того, как пройдет время d t , обе эти величины получат приращение (соответственно d m и d v , причем значение d m будет меньше 0 ). Тогда количество движения, совершаемого ракетой, станет равно:
( m + d m ) ( v + d v ) .
Нам необходимо учитывать тот момент, что за время d t также происходит движение газов. Это количество тоже нужно добавить в формулу. Оно будет равно d m г а з v г а з . Первый показатель означает массу газов, которые образуются за указанное время, а второй – их скорость.
Теперь нам нужно найти разность между суммарным количеством движения за время t + d t и количеством движения системы во время t . Так мы найдем приращение данной величины за время d t , которое будет равно F d t (буквой F обозначена геометрическая сумма всех тех внешних сил, которые действуют в это время на ракету).
В итоге мы можем записать следующее:
( m + d m ) ( v + d v ) + d m г а з + v г а з — m v = F d t .
Поскольку нам важны именно предельные значения d m d t , d v d t и их производные, приравняем эти показатели к нулю. Значит, после раскрытия скобок произведение d m · d v может быть отброшено. С учетом сохранения массы получим:
d m + d m г а з = 0 .
Теперь исключим массу газов d m г а з и получим скорость, с которой газы будут покидать ракету (скорость струи вещества), выражающаяся разностью v о т н = v г а з — v . Учитывая эти преобразования, можно переписать исходное уравнение в следующем виде:
d m v = v о т н d m + F d t .
Теперь разделим его на d t и получим:
m d v d t = v о т н d m d t + F .
Уравнение Мещерского
Форма полученного уравнения точно такая же, как у уравнения, выражающего второй закон Ньютона. Но, если там мы имеем дело с постоянной массой тела, то здесь из-за потери вещества она постепенно меняется. К тому же помимо внешней силы нужно учитывать так называемую реактивную силу. В примере с ракетой это будет сила выходящей из нее газовой струи.
Уравнение m d v d t = v о т н d m d t + F впервые вывел русский механик И.В. Мещерский, поэтому оно получило его имя. Также его называют уравнением движения тела с переменной массой.
Формула Циолковского
Попробуем исключить из уравнения движения ракеты внешние силы, воздействующие на нее. Предположим, что движение ракеты прямолинейно, а направление противоположно скорости газовой струи v о т н . Будем считать направление полета положительным, тогда проекция вектора v о т н является отрицательной. Она будет равна — v о т н . Переведем предыдущее уравнение в скалярную форму:
m d v = v о т н d m .
Тогда равенство примет вид:
d v d m = — v о т н m .
Газовая струя может выходить во время полета с переменной скоростью. Проще всего, разумеется, принять ее в качестве константы. Такой случай наиболее важен для нас, поскольку так уравнение решить намного проще.
Исходя из начальных условий, определим, какое значение приобретет постоянная интегрирования С. Допустим, что в начале пути скорость ракеты будет равна 0 , а масса m 0 . Следовательно, из предыдущего уравнения можем вывести:
C = v о т н ln m 0 m .
Тогда мы получим соотношения следующего вида:
v = v о т н ln m 0 m или m 0 m = e v v о т н .
Это соотношение и является формулой Циолковского.
Она предназначена для расчета запаса топлива, с помощью которого ракета может набрать необходимую скорость. При этом время сгорания топлива не обусловливает величину максимальной скорости ракеты. Чтобы разогнаться до предела, нужно увеличить скорость истечения газов. Для достижения первой космической скорости следует изменить конструкцию ракеты. Она должна быть многоступенчатой, поскольку необходимо меньшее соотношение между требуемой массой топлива и массой ракеты.
Разберем несколько примеров применения данных построений на практике.
Условие: у нас есть космический корабль, скорость которого постоянна. Для изменения направления полета в ней нужно включить двигатель, который выбрасывает газовую струю со скоростью v о т н . Направление выброса перпендикулярно траектории корабля. Определите угол изменения вектора скорости при начальной массе корабля m 0 и конечной m .
Решение
Ускорение по абсолютной величине будет равно a = ω 2 r = ω v , причем v = c o n s t .
Значит, уравнение движения будет выглядеть так:
m d v d t = v о т н d m d t перейдет в m v ω d t = — v о т н d m .
Поскольку d a = ω d t является углом поворота за время d t , то после интеграции первоначального уравнения получим:
a = v о т н v ln m 0 m .
Ответ: искомый угол будет равен a = v о т н v ln m 0 m .
Условие: масса ракеты перед стартом равна 250 к г . Вычислите высоту, которую она наберет через 20 секунд после начала работы двигателя. Известно, что топливо расходуется со скоростью 4 к г / с , а скорость истечения газов постоянна и равна 1500 м / с . Поле тяготения Земли можно считать однородным.
Решение
Начнем с записи уравнения Мещерского. Оно будет иметь следующий вид:
m ∆ v 0 ∆ t = μ v о т н — m g .
Здесь m = m 0 — μ t и v 0 – скорость ракеты в заданный момент времени. Разделим переменные:
∆ v 0 = μ v о т н m 0 — μ t — g ∆ t .
Теперь решим полученное уравнение с учетом первоначальных условий:
v 0 = v о т н ln m 0 m 0 — μ t — g t .
С учетом того, что H 0 = 0 при t = 0 , у нас получится:
H = v о т н t — g t 2 2 + v о т н m 0 μ 1 — μ t m 0 ln 1 — μ t m 0 .
Добавим заданные значения и найдем ответ:
H = v о т н t — g t 2 2 + v о т н m 0 μ 1 — μ t m 0 ln 1 — μ t m 0 = 3177 , 5 м .
Ответ: через 20 секунд высота ракеты будет составлять 3177 , 5 м .
Сохранение импульса, уравнение Мещерского и банджи-джампинг
Очень редко появляются совсем новые сюжеты задач механики. Но сейчас такое произошло. Движение прыгуна в экстремальном аттракционе банджи-джампинг обладает некоторыми удивительными особенностями, которые требуют объяснения. Оказалось, что это можно сделать, если применить к прыгуну и привязанному к нему канату уравнение, выведенное нашим соотечественником еще в позапрошлом веке.
Экстремальный аттракцион
В телевизионных репортажах из дальних стран уже неоднократно рассказывалось о таком экстремальном развлечении: к ногам человека привязывают свободной конец упругого каната, другой конец которого закрепляют, после чего человека сталкивают с большой высоты (рис. 1). Это и есть банджи-джампинг. Много ссылок на этот аттракцион дает Интернет, попал он уже и в Википедию. Будем для простоты называть его просто джампингом. В этом прыжке много разных фаз, и, соответственно, много удовольствий поджидает прыгуна. Но нас сейчас интересует только одно обстоятельство — видеосъемка показала, что человек летит вниз с ускорением, превышающим ускорение свободного падения g. На первый взгляд, это представляется удивительным — ведь, казалось бы, прыгун и часть каната ускоряются только силой тяжести, никаких других сил обнаружить не удается.
Однако начнем с самого начала. Выясним, к какому типу систем можно отнести прыгуна с канатом и какие законы (уравнения) надо использовать для описания динамики такой системы.
Прыгун и движущаяся часть каната — это типичный пример тела с переменной массой. Во избежание недоразумений надо сказать, что речь идет об изменении массы тела за счет отсоединения какой-то его части (или присоединения извне). В нашем случае при движении непрерывно увеличивается покоящаяся часть каната и, соответственно, уменьшается масса движущейся его части. Это очевидное обстоятельство и окажется важнейшим для наших дальнейших рассуждений.
Поставим самые напрашивающиеся вопросы. Что происходит с импульсом системы? Что происходит с ее механической энергией? Как записывается основное уравнение динамики для такой системы?
Попытаемся ответить на все эти вопросы. Но прежде рассмотрим совсем простой, но очень важный для наших рассуждений пример.
Щелканье кнута и закон сохранения импульса
В раннем-раннем детстве я видел в дачном поселке под Ленинградом, как местные жители встречали вечером стадо коров (позднее коров в дачной местности уже не было). Подгоняя буренок, пастух щелкал кнутом. Вот оно!
Молодому читателю, возможно, надо напомнить, как устроен кнут. А устроен он очень просто: к палке (рукоятке, кнутовищу) привязан узкий длинный ремень (иногда — веревка). Это «устройство» называют еще бичом. Так, в известном стихотворении Н. А. Некрасова эти слова стоят рядом:
Там били женщину кнутом,
Крестьянку молодую.
Ни звука из ее груди,
Лишь бич свистал, играя.
Двинув кнутовище, пастух сообщает всему ремню импульс — а дальше начинается самое для нас интересное. Конец ремня, привязанный к остановившемуся кнутовищу, тормозится, и всё меньшая часть ремня продолжает движение (рис. 2). Но в точке перегиба никакая сила на движущуюся часть ремня не действует, значит, ее импульс не изменяется. А поскольку масса этой части ремня уменьшается, то скорость ее должна увеличиваться. Таким образом, движущаяся часть ремня непрерывно ускоряется. По-видимому, конец ремня даже переходит через скорость звука — и раздается характерный очень громкий щелчок.
Человек, привыкший к рассуждениям, основанным на втором законе Ньютона, может спросить: «Какая же сила ускоряет часть кнута?» В том-то и дело, что никакие внешние силы к ускорению части кнута не имеют отношения. А движущаяся часть ремня непрерывно ускоряется потому, что этого требует закон сохранения импульса. Аналогия с движением каната в джампинге совершенно очевидна. Привяжите к концу ремня какое-нибудь тело — аналогия станет еще нагляднее. Но в джампинге в дело вмешивается еще и сила тяжести. Значит, в общем случае нам надо иметь уравнение, описывающее движение тела переменной массы под действием внешних сил. В одном крайнем случае (в отсутствие внешних сил) уравнение должно обеспечивать сохранение импульса, как в случае с кнутом, в другом (при неизменной массе) — переходить в обычный второй закон Ньютона.
Порядок в этом вопросе навел еще в позапрошлом веке российский ученый Иван Всеволодович Мещерский.
Уравнение Мещерского
Иван Всеволодович Мещерский родился в Архангельске в 1859 году. С 1878 по 1882 год он учился на математическом отделении физико-математического факультета Петербургского университета. После окончания был оставлен в университете для подготовки к профессорскому званию. Первые результаты по интересующей нас теме относятся к 1893 году. В 1897 году Мещерский защищает магистерскую диссертацию на тему «Динамика точки переменной массы». Некоторые дополнительные результаты были опубликованы в 1904 году в работе «Уравнения движения точки переменной массы в общем случае». Эти работы были включены в книгу И. В. Мещерского «Работы по механике тел переменной массы», изданную в 1949 году в серии «Классики естествознания». Именно это издание есть в моей личной библиотеке. (Несколько раз я приносил эту книгу в класс, чтобы показать ученикам, как удручающе громоздки уравнения механики, если они записаны без использования векторных обозначений.)
Мещерский оставил след не только как ученый, но и как выдающийся педагог высшей школы. С 1902 года до конца своих дней он возглавлял кафедру теоретической механики в Петербургском политехническом институте. Удивительна судьба выпущенного в 1914 году «Сборника задач по теоретической механике», составленного группой преподавателей под руководством И. В. Мещерского. У меня на полке стоит 33-е издание этого задачника, увидевшее свет в 1973 году, т. е. менее чем за 60 лет книга выдержала 33 издания! Другого такого примера я не знаю. А ведь в 1973 году история задачника отнюдь не закончилась. Многие сюжеты, которые нам сейчас известны по школьным и вузовским задачникам, впервые появились именно в этой книге.
Теперь — об уравнении Мещерского. Кратко напомним основополагающие моменты. Согласно Мещерскому, основной закон динамики тела переменной массы записывается в виде

где 



Это, как уже сказано, и есть дифференциальное уравнение второго порядка (звучит пугающе). Математики умеют решать такие уравнения, выполняя формальные преобразования, придумывая замены переменных и тому подобное. Но мы же физики — мы пойдем своим путем.
Подумаем: какого типа движение может совершать свешивающийся участок цепи? О равномерном не может быть и речи. Может быть — равноускоренное? Что ж, попробуем.
Предположим, что свешивающийся со стола участок цепи движется с неким неизвестным нам пока постоянным ускорением a (a 0 больше ускорения свободного падения g и растет со временем. Качественно картина явления представляется нам вполне ясной: тело с уменьшающейся массой приобретает под действием силы тяжести всё больший импульс, а значит — ускоряется. И этот эффект будет тем сильнее, чем больше масса каната (по сравнению с массой прыгуна).
Новый опыт
Снова вернемся к понятию реактивной силы. В элементарных курсах физики реактивную силу, приводящую в движение ракету, обычно объясняют как силу давления продуктов сгорания топлива на стенку камеры сгорания. Представляется, что иногда такое «объяснение» может затемнять суть дела.
Рассмотрим совсем простой, «школьный» опыт. В кузов игрушечного автомобиля поместим длинную тяжелую ленту. Она должна быть свернута таким образом, чтобы иметь возможность разматываться и покидать кузов с минимальным трением. Закрепим конец ленты на демонстрационном столе и толкнем автомобиль. Лента, покидая кузов и останавливаясь, не уносит импульс, и, следовательно, импульс автомобиля с остатком ленты не меняется. Но масса-то уменьшается! Значит, скорость должна увеличиваться. Итак, лента разматывается — и автомобильчик разгоняется!
Ясно, что никакой реактивной силы, толкающей автомобильчик вперед, обнаружить не удается (нет никакого давления на стенку кузова). «Но это то же самое, что кнут!» — может сказать читатель. Ну да! Тем удивительнее, что никакого упоминания о таком опыте я никогда не видел. Удастся ли реально продемонстрировать этот опыт, зависит от того, сможет ли экспериментатор уменьшить силу трения — с одной стороны, между автомобилем и столом и, с другой стороны, между лентой и кузовом — до необходимых значений. Указание экспериментатору: при сматывании ленты не должна меняться ее высота над столом, а автомобильчик должен быть легким (по сравнению с лентой).
Автору было бы очень интересно услышать об успехах в проведении этого опыта.
http://zaochnik.com/spravochnik/fizika/osnovy-dinamiki/dvizhenie-tela-s-peremennoj-massoj/
http://elementy.ru/nauchno-populyarnaya_biblioteka/431740/Sokhranenie_impulsa_uravnenie_Meshcherskogo_i_bandzhi_dzhamping