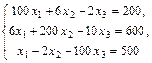Уравнение метод итераций в mathcad

Уравнение метод итераций в mathcad

Задача 1-10. Найти методом итераций действительные корни уравнения с пятью верными знаками. Задачу необходимо решить аналитически и в системе Mathcad .

Метод приближенного нахождения корней уравнения (в том числе нелинейного), известный как метод простой итерации состоит в том, что за каждое следующее приближение аргумента принимается значение вспомогательной функции при предыдущем значении аргумента.

Характер сходимости и сам факт сходимости метода зависит от выбора начального приближения корня х ₀ .

Другим важным фактором является выбор функции .

Эта функция может быть получена путем различного выражения переменной х из исходного уравнения.

Например, для уравнения можно принять .

Рассмотрим пример задания контрольной работы.

Методом итераций решить уравнение с точностью до 10 -5 .

Рассмотрим простейшее решение в системе MathCad .

Вводится с клавиатуры:

Здесь задаются коэффициенты заданного уравнения и начальное количество шагов итерации. Это количество может впоследствии корректироваться до достижения требуемой точности. В качестве начального значения можно взять 10-15 шагов.

Затем задается функция :

Далее вводится сама функция:

Вводится диапазон изменения индекса приближений i :

Для этого с клавиатуры надо ввести i :1; n

Важным фактором является определение значение начального приближения х ₀ .

Достаточным условием сходимости метода является выполнение неравенства

В нашем случае

Но необходимым это условие не является.

В предлагаемом примере за начальное приближение примем абсциссу вершины параболы

Для получения значений невязок метода вводим переменную

uravnenie :=a*x 2 +b* x+c ,

которая будет показывать насколько значение квадратичной функции отличается от 0.

Если ниже ввести х= , то появится таблица значений приближений аргумента.

Если ввести uravnenie = ,то появится таблица невязок.

Можно также найти значения корней по известным формулам корней квадратного уравнения.

На рис. 1 показано, как ввести выражение для koren 1 и koren 2 .

Для построения графиков функции и в MathCad выбирается шаблон графика, в ячейке для переменной вводится x , в ячейке для функции f ( x ), x .

Изменяя количество итераций n можно получать значения с различной степенью точности.

Примечание. Значения, получаемые в таблицах, по умолчанию имеют три знака после десятичной запятой. Для того , чтобы изменить число знаков, надо дважды щелкнуть левой кнопкой мыши на таблице и в появившемся меню ввести необходимое число знаков после запятой.

В среде Maple решение этой же задачи выглядит так (рис.2):

Ниже показан вывод расчета программы с пятого по последний (11-й) шаг, на котором была достигнута требуемая точность.

Однако при решении подобной задачи могут возникнуть сложности, которые на первый взгляд кажутся непреодолимыми.

Рассмотрим пример, который практически не отличается от предыдущего.

Решается уравнение .

Попробуем использовать Mathcad , как было показано выше (рис.3) :

Как видно, значения невязок стремительно возрастают даже при пяти итерациях. При увеличении числа итераций Mathcad вообще не производит расчетов, т.к. значения вычисляемых параметров превышают допустимые для Mathcada величины.

Из теории известно, что сходимость метода итераций зависит от выбора начального приближения. Однако, попытки менять значения х ₀ ни к чему не приводят. Метод все равно расходится.

В этом случае нужно менять порядок расчетов.

Попробуем выразить переменную х из уравнения иначе:

Как видно, проблема решена.

Для нахождения второго корня вводим :

Рассмотренный пример показывает, что для решения поставленной задачи не следует применять Mathcad формально, используя готовые шаблоны и решения. Применение численного метода даже к концептуально идентичной задаче требует понимания особенностей метода и порядка вычислений.

Проверка метода простой итерации в MathCad

Теоретическая часть

Метод простой итерации

с отделенным корнем X [a, b]. Для решения уравнения методом простой итерации приведем его к равносильному виду:

Это всегда можно сделать, причем многими способами. Например: x=g(x) · f(x) + x ≡ φ(x), где g(x) — произвольная непрерывная функция, не имеющая корней на отрезке [a,b].

Пусть x (0) — полученное каким-либо способом приближение к корню x (в простейшем случае x (0) =(a+b)/2). Метод простой итерации заключается в последовательном вычислении членов итерационной последовательности:

начиная с приближения x (0) .

Утверждение: Если последовательность метода простой итерации сходится и функция φ непрерывна, то предел последовательности является корнем уравнения x=φ(x)

Перейдем к пределу в равенстве x (k+1) =φ(x (k) ) Получим с одной сторонv по , что а с другой стороны в силу непрерывности функции φ.

В результате получаем x * =φ(x * ). Следовательно, x * — корень уравнения, т.е. X=x * .

Чтобы пользоваться этим утверждением нужна сходимость последовательности . Достаточное условие сходимости дает:

Теорема(о сходимости) Пусть уравнение x=φ(x) имеет единственный корень на отрезке [a,b] и выполнены условия:

1) φ(x) C 1 [a,b];

2) φ(x) [a,b] x [a,b];

3) существует константа q > 0: | φ ‘(x) | ≤ q (k) >, заданная формулой x (k+1) = φ(x (k) ), k=0, 1, . сходится при любом начальном приближении x (0) [a,b].

Доказательство Рассмотрим два соседних члена последовательности : x (k) = φ(x (k-1) ) и x (k+1) = φ(x (k) ) Tак как по условию 2) x (k) и x (k+1) лежат внутри отрезка [a,b], то используя теорему Лагранжа о средних значениях получаем:

x (k+1) — x (k) = φ(x (k) ) — φ(x (k-1) ) = φ ‘(c _k )(x (k) — x (k-1) )

где c _k (x (k-1) , x (k) ).

Если мы докажем, что этот ряд сходится, то значит сходится и последовательность его частичных сумм
S_k = x (0) + ( x (1) — x (0) ) + . + ( x (k) — x (k-1) ).

Но нетрудно вычислить, что

Следовательно, мы тем самым докажем и сходимость итерационной последовательности .

Для доказательства сходимости pяда сравним его почленно (без первого слагаемого x (0) ) с рядом

который сходится как бесконечно убывающая геометрическая прогрессия (так как по условию q (0) >

Получим формулу, дающую способ оценки погрешности |X — x (k+1) | метода простой итерации.

Имеем X — x (k+1) = X — S_k+1 = S_∞ — S_k+1 = (x (k+2) — (k+1) ) + (x (k+3) — x (k+2) ) + . . Следовательно |X — x (k+1) | ≤ |x (k+2) — (k+1) | + |x (k+3) — x (k+2) | + . ≤ q k+1 |x (1) — x (0) | + q k+2 |x (1) — x (0) | + . = q k+1 |x (1) — x (0) | / (1-q)

В результате получаем формулу

Взяв за x (0) значение x (k) , за x (1) — значение x (k+1) (так как при выполнении условий теоремы такой выбор возможен) и учитывая, что при имеет место неравенство q k+1 ≤ q выводим:

|X — x (k+1) | ≤ q k+1 |x (k+1) — x (k) | / (1-q) ≤ q|x (k+1) — x (k) | / (1-q)

Итак, окончательно получаем:

Используем эту формулу для вывода критерия окончания итерационной последовательности. Пусть уравнение x=φ(x) решается методом простой итерации, причем ответ должен быть найден с точностью ε , то есть |X — x (k+1) | ≤ ε. С учетом получаем, что точность ε будет достигнута, если выполнено неравенство

Tаким образом для нахождения корней уравнения x=φ(x) методом простой итерации с точностью нужно продолжать итерации до тех пор, пока модуль разности между последними соседними приближениями остается больше числа ε(1-q)/q.

Замечание: В качестве константы q обычно берут оценку сверху для величины

Пример: Составим последовательность для решения уравнения f(x)=x·e x =0 по методу простой итерации.

Приведем уравнение к итерационному виду:

Далее графически произведем отделение корня.

Несложный анализ графика показывает, что корень X [e -1 ,1]. Tак как при x [e -1 ,1] и e -x [e -1 ,1] , x [e -1 ,1], то в соответствии с теоремой итерационная последовательность x (k+1) = e — x(k) , k=0, 1, 2, . гарантированно сходится к корню уравнения. В качестве начального приближения к корню можно взять x (0) =0.5(1+e -1 ).

Блок схема

Проверка метода простой итерации в MathCad

Для использования метода итерации исходное нелинейное уравнение f(х) = 0 заменяется равносильным уравнением

Пусть известно начальное приближение корня х = х₀. Подставляя это значение в правую часть уравнения, получим новое приближение:

Далее, подставляя каждый раз новое значение корня в, получаем последовательность значений:

Геометрически метод итерации может быть пояснен следующим образом. Построим на плоскости хОу графики функций у = х и у = j (х). Каждый действительный корень уравнения является абсциссой точки пересечения М кривой у = j (х) с прямой у = х (Рис.2, а).

Отправляясь от некоторой точки А₀ [x₀, j (x₀)], строим ломаную А₀В₁А₁В₂А₂… (“лестница”), звенья которой попеременно параллельны оси Ох и оси Оу, вершины А₀, А₁, А₂, …лежат на кривой у=j (х), а вершины В₁, В₂, В₃, …, — на прямой у = х. Общие абсциссы точек А₁ и В₁, А₂ и В₂, …, очевидно, представляют собой соответственно последовательные приближения х₁, х₂, … корня .

Возможен также другой вид ломаной А₀В₁А₁В₂А₂ … – “спираль” (Рис.2, б). Решение в виде “лестницы” получается, если производная j’ (х) положительна, а решение в виде “спирали”, если j’ (х) отрицательна.

На Рисунке 6, а, б кривая у = j (х) в окрестности корня — пологая, то есть 1, то процесс итерации может быть расходящимся (Рис.3).

Поэтому для практического применения метода итерации нужно выяснить достаточные условия сходимости итерационного процесса.

Теорема:Пусть функция j (х) определена и дифференцируема на отрезке [a, b], причем все ее значения j (х) [a, b].

Тогда, если существует правильная дробь q такая, что

q 3 – x – 1 = 0

имеет корень x [1, 2], так как f(1) = — 1 0.

Уравнение можно записать в виде

j (х) = х 3 – 1 и j’ (х) = 3х 2 ;

j’ (х) 3 при 1 х 2

и, следовательно, условия сходимости процесса итерации не выполнены.

Если записать уравнение в виде

.

Отсюда при 1 х 2 и значит, процесс итерации для уравнения быстро сойдется.

Найдем корень x уравнения с точностью до 10 -2 . Вычисляем последовательные приближения х_n с одним запасным знаком по формуле

С точностью до 10 -2 можно положить x = 1,324.

Создание программы

Для начала мы создаем Form1 с использованием TextBox и Label. TextBox используется для ввода данных: начала промежутка, конца промежутка и погрешность. А также для решение уравнения. Label используется для обозначения различных данных.

Form1.

Также мы создаем меню. При помощи Menu Editor Мы создаем четыре основных пункта: Файл, Решение, График, Справка. Файл будет открывать два подпункта: Сохранить, который будет сохранить изменения программы на диске, и Выход, который будет выходить из Form1. Решение будет выводит на последний TextBox решение уравнение по заданным данным. График будет переводить на Form2. Справка будет выводит подпункт О программе…,в которой будет говорится о созданной программе.

Метод простых итераций

Дата добавления: 2015-07-23 ; просмотров: 7328 ; Нарушение авторских прав

Лабораторная работа №5

Тема: Решение СЛАУ итерационным методом в MathCAD.

Цель: изучение приемов численного решения систем линейных уравнений с помощью функций MathCAD.

Порядок выполнения работы

1. Ознакомиться с теоретическими положениями.

2. Рассмотреть пример решения СЛАУ итерационным методом в MathCAD.

3. Выполнить практическое задание.

4. Ответить на контрольные вопросы.

Содержание отчета

1. Тема, цель работы.

2. Практическое задание:

2.1. Постановка задачи.

2.2. Результаты выполнения.

3. Ответы на контрольные вопросы.

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

Итерационные методы – это методы, позволяющие получить решение системы с заданной точностью путем сходящихся итерационных процессов (метод итерации, метод Зейделя и др.).

Вследствие неизбежных округлений результаты даже точных методов являются приближенными. При использовании итерационных методов, сверх того, добавляется погрешность метода.

Эффективное применение итерационных методов существенно зависит от удачного выбора начального приближения и быстроты сходимости процесса.

Метод простых итераций

Пусть дана линейная система (1).

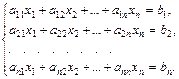(1)

Систему (1) коротко можно записать в виде матричного уравнения:

Предполагая, что диагональные коэффициенты

разрешим первое уравнение системы (1) относительно х₁, второе – относительно х₂ и т. д. Тогда получим эквивалентную систему

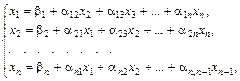(3)

при i ¹ j

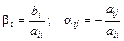
Систему (3) можно записать в матричной форме

x = b + ax,

а любое (k + 1) приближение вычисляется по формуле

Напишем формулы приближений в развернутом виде:

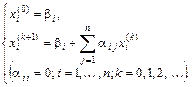(4¢)

Приведем достаточное условие сходимости метода итераций.

Теорема:Процесс итерации для приведенной линейной системы (18) сходится к единственному ее решению, если какая-нибудь каноническая норма матрицы a меньше единицы, т.е. для итерационного процесса (19) достаточное условие есть

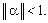(5)

Следствие 1. Процесс итерации для системы (3) сходится, если:

1) (k +1) .

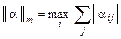
Пример решения СЛАУ итерационным методом в MathCAD.

Решить систему методом простых итераций:

Результат на экране:

Не нашли то, что искали? Google вам в помощь!