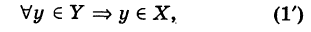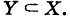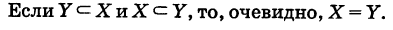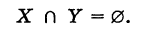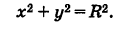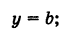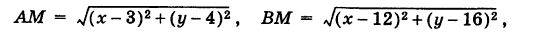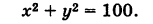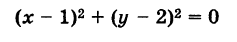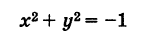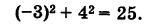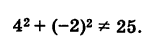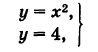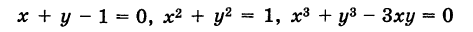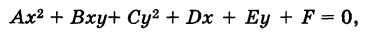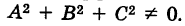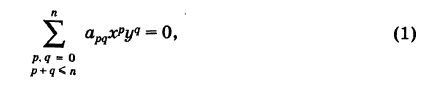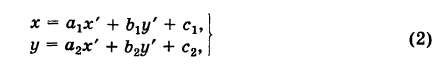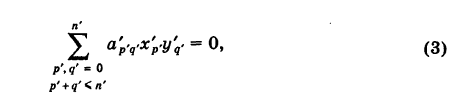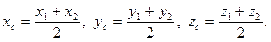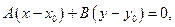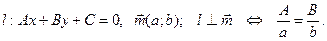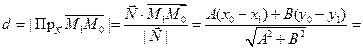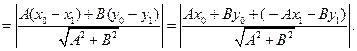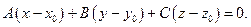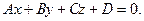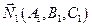Уравнение линии — определение с примерами решения
Содержание:
Множества:
Под множеством X = <х, х\ х", . >понимается собрание (совокупность) некоторых элементов х, х\ х’\ . . Если х есть элемент множества X, то пишут х € X (читается: х принадлежит X); если у не является элементом множества X, то пишут у t X (читается: у не принадлежит множеству X).
Пример:
X — множество всех студентов в данной аудитории.
Пример:
Х = <1,2, 3, . >— множество натуральных чисел.
Удобно ввести понятие пустого множества
Пример:
Множество трехголовых людей пусто.
Множества X и X’ считаются равными, т. е. X = X’, если они состоят из одних и тех же элементов.
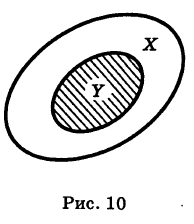
Определение: Множество У, состоящее из части элементов множества X или совпадающее с ним, называется подмножеством множества X; в этом случае пишут
Условились считать, что пустое множество есть подмножество любого множества.
Если множества изображать «логическими фигурами», то соотношению (1) соответствует рис. 10.
Если под символом V понимать «для любого», то соотношение (1) эквивалентно следующему:
где стрелка 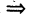
Пример:
Пусть X — множество всех студентов первого курса, У — множество студенток первого курса. Очевидно,
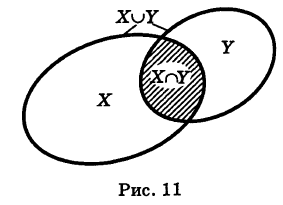
Определение: Под объединением (суммой) двух множеств X и Y понимается множество X U У (U — знак объединения), состоящее из всех элементов, принадлежащих хотя бы одному из данных множеств, т. е. входящих или в X, или в У, или в X и в У одновременно (рис. 11).
Аналогично определяется объединение большего числа множеств. Так, под объединением X U У U Z трех множеств понимается множество всех элементов, принадлежащих хотя бы одному из множеств X, У, Z. Логически знак объединения множеств соответствует союзу «или» (соединительному).
Определение: Под пересечением (произведением) двух множеств X и У понимается множество 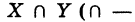
Таким образом, знак пересечения множеств логически соответствует союзу «и». Если множества X и У не имеют общих элементов, то их пересечение пусто:
Аналогично определяется пересечение большего числа множеств. Так, под пересечением 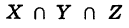
Например: <1, 2, 3> 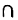
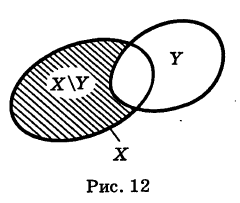
Определение: Для множеств X и У под их разностью Х\У понимается множество, содержащее все элементы множества X, не входящие в множество У (рис. 12).
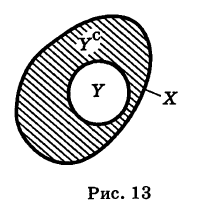
Если У X, то множество Ус = Х\У называется дополнением множества У до множества X (рис. 13).
Очевидно, 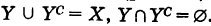
Например: <1, 2, 3>\ <2, 3, 4>= <1>.
Метод координат на плоскости
Раздел математики, занимающийся изучением свойств геометрических фигур с помощью алгебры, носит название аналитической геометрии, а использование для этой цели координат называется методом координат.
Выше мы применили метод координат для решения ряда важных, но частных задач. Теперь мы приступим к систематическому изложению того, как в аналитической геометрии решается общая задача, состоящая в исследовании методами математического анализа формы, расположения и свойств данной линии.
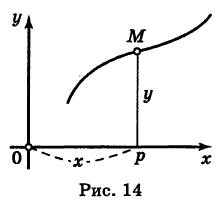
Пусть мы имеем некоторую линию на плоскости (рис. 14). Координаты х и у точки М, лежащей на этой линии, не могут быть вполне произвольными; они должны быть подчинены известным ограничениям, обусловленным геометрическими свойствами данной линии. Тот факт, что числа х и у являются координатами точки, лежащей на данной линии, аналитически записывается в виде некоторого уравнения. Это уравнение называется уравнением линии на плоскости.
Сущность метода координат на плоскости заключается в том, что всякой плоской линии сопоставляется ее уравнение1*, а затем свойства этой линии изучаются путем аналитического исследования соответствующего уравнения.
Линия как множество точек
Линия на плоскости обычно задается как множество точек, обладающих некоторыми геометрическими свойствами, исключительно им присущими.
Пример:
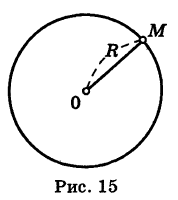
Окружность радиуса R (рис. 15) есть множество всех точек плоскости, удаленных на расстояние R от некоторой ее точки О (центр окружности).
Иными словами, на окружности расположены те и только те точки, расстояние которых от центра окружности равно ее радиусу.
Пример:
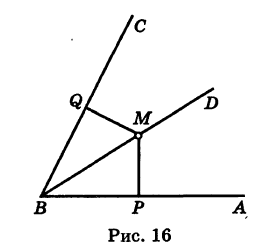
Биссектриса угла ABC (рис. 16) есть множество всех точек, лежащих внутри угла и равноудаленных от его сторон. Этим утверждается, что: 1) для каждой точки М, лежащей на биссектрисе BZ), длины перпендикуляров MP и MQ, опущенных соответственно на стороны ВА и ВС угла, равны между собой: MP = MQ, и 2) всякая точка, находящаяся внутри угла ABC и не лежащая на его биссектрисе, будет ближе к одной стороне угла, чем к другой.
Уравнение линии на плоскости
Сформулируем теперь точнее определение уравнения линии1* на плоскости.
Определение: Уравнением линии (уравнением кривой) на плоскости Оху называется уравнение, которому удовлетворяют координаты х и у каждой точки данной линии и не удовлетворяют координаты любой точки, не лежащей на этой линии.
Таким образом, для того чтобы установить, что данное уравнение является уравнением некоторой линии К, необходимо и достаточно: 1) доказать, что координаты .любой точки, лежащей на линии К у удовлетворяют этому уравнению, и 2) доказать, обратно, что если координаты некоторой точки удовлетворяют этому уравнению, то точка обязательно лежит на линии К.
Отсюда уже автоматически будет следовать, что: 1′) если координаты какой-нибудь точки не удовлетворяют данному уравнению, то точка эта не лежит на линии К, и 2′) если точка не лежит на линии К, то ее координаты не удовлетворяют данному уравнению.
Если точка М (*, у) передвигается по линии К, то ее координаты х и у, изменяясь, все время удовлетворяют уравнению этой кривой. Поэтому координаты точки М (х, у) называются текущими координатами точки линии К.
На плоскости Оху текущие координаты точки М данной кривой К обычно обозначаются через х и у, причем первая из них есть абсцисса точки М, а вторая — ее ордината. Однако, если это целесообразно, текущие координаты точки М можно обозначать.
Линию мы часто будем называть кривой независимо от того, прямолинейна она или не прямолинейна любыми буквами, например М (X, У) или М 
где точки N (х, у) и N (X, У) расположены на плоскости Оху, представляют собой уравнение одной и той же прямой на этой плоскости.
Основное понятие аналитической геометрии — уравнение линии — поясним на ряде примеров.
Пример:
Составить уравнение окружности данного радиуса R с центром в начале координат.
Решение:
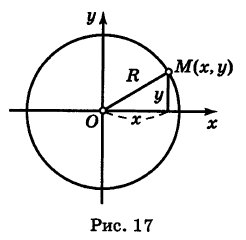
Возьмем на окружности (рис. 17) произвольную точку М (х, у) и соединим ее с центром О. По определению окружности имеем ОМ = R,
т. е. 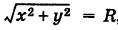
Уравнение (1) связывает между собой координаты х и у каждой точки данной окружности. Обратно, если координаты точки М (х, у) удовлетворяют уравнению (1), то, очевидно, ОМ = R и, следовательно, эта точка лежит на нашей окружности. Таким образом, уравнение (1) представляет собой уравнение окружности радиуса R с центром в начале координат.
Пример:
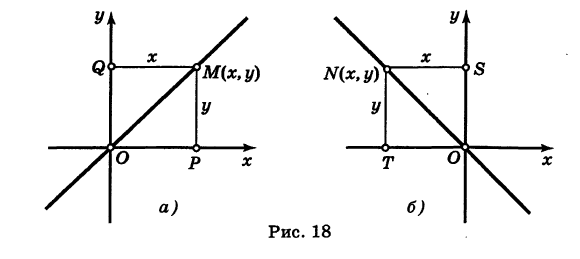
Составить уравнения биссектрис координатных углов.
Решение:
Рассмотрим сначала биссектрису I и III координатных углов (рис. 18, а). Возьмем на ней произвольную точку М (х, у). Если точка М лежит в I квадранте, то абсцисса и ордината ее обе положительны и равны между собой (по свойству биссектрисы). Если же точка М (jc, у) лежит в III квадранте, то абсцисса и ордината будут обе отрицательны, а модули их равны, поэтому будут равны и координаты хм у этой точки. Следовательно, в обоих случаях имеем
Обратно, если координаты х и у какой-нибудь точки М (х, у) удовлетворяют уравнению (2), то эта точка, очевидно, лежит на биссектрисе
I и III координатных углов. Поэтому уравнение (2) представляет собой уравнение биссектрисы I и III координатных углов.
Рассмотрим теперь биссектрису II и IV координатных углов (рис. 18, б). Возьмем на ней произвольную точку N (х, у). В каком бы квадранте — II или IV — ни была расположена эта точка, координаты ее х и у равны по модулю и отличаются знаками.
Следовательно, в обоих случаях имеем
Обратно, если для какой-нибудь точки N (,х, у) выполнено уравнение (3), то эта точка, очевидно, лежит на биссектрисе II и IV координатных углов. Таким образом, уравнение (3) есть уравнение биссектрисы II и IV координатных углов.
Пример:
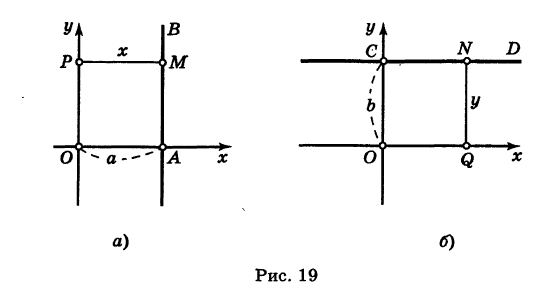
Составить уравнение прямой, параллельной оси ординат.
Решение:
Пусть прямая АВ || О у и пусть отрезок OA = а (рис. 19, а). Тогда для любой точки М (х, у) прямой АВ ее абсцисса х равна а:
Обратно, если абсцисса некоторой точки М (х, у) равна а, то эта точка лежит на прямой АВ.
Таким образом, уравнение (4) представляет собой уравнение прямой, параллельной оси Оу и отстоящей от нее на расстоянии, равном числовому значению а; при этом если прямая расположена справа от оси Оу, то а положительно; если же прямая расположена слева от оси Оу, то а отрицательно.
В частности, при а = 0 получаем уравнение оси ординат: х = 0.
Пример:
Составить уравнение прямой, параллельной оси абсцисс.
Решение:
Совершенно аналогично, если прямая CD || Ох и ОС = Ь (рис. 19, б), то ее уравнение будет
при этом если прямая CD расположена выше оси Оху то Ъ положительно, если же прямая CD расположена ниже оси Ох, то b отрицательно.
В частности, при b = 0 получаем уравнение оси абсцисс: у = 0.
Пример:
Найти линию, расстояние точек которой от точки В (12, 16) в два раза больше, чем от точки А (3, 4).
Решение:
Если М (х, у) — произвольная точка искомой линии, то согласно условию задачи имеем
Чтобы составить уравнение этой линии, надо выразить AM и ВМ через координаты х и у точки М. На основании формулы расстояния между двумя точками имеем
откуда, согласно соотношению (5),
Это и есть уравнение искомой линии.
Но в таком виде трудно судить, какую линию представляет это уравнение, поэтому упростим его. Возведя обе части в квадрат и раскрыв скобки, получим
или после несложных преобразований имеем равносильное уравнение
Сравнивая полученное уравнение с уравнением (1), мы видим, что искомая линия является окружностью радиуса 10 с центром в начале координат.
Построение линии по ее уравнению
Если переменные х и у связаны некоторым уравнением, то множество точек М (х, у), координаты которых удовлетворяют этому уравнению, представляет собой, вообще говоря, некоторую линию на плоскости (геометрический образ уравнения).
В частных случаях эта линия может вырождаться в одну или несколько точек. Возможны также случаи, когда уравнению не соответствует никакое множество точек.
соответствует единственная точка (1, 2), так как этому уравнению удовлетворяет единственная пара значений: х = 1 и у = 2.
не соответствует никакое множество точек, так как этому уравнению нельзя удовлетворить никакими действительными значениями x и у.
Зная уравнение линии, можно по точкам построить эту линию.
Пример:
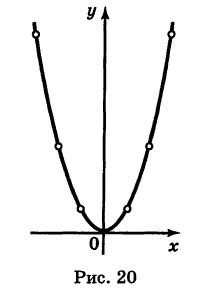
Построить линию, выражаемую уравнением
(обычно говорят короче: построить линию у = х 2 ).
Решение:
Давая абсциссе х в уравнении (1) числовые значения и вычисляя соответствующие значения ординаты у, получим следующую таблицу:
Нанося соответствующие точки на плоскость, мы видим, что конфигурация этих точек определяет начертание некоторой линии; при этом чем гуще построена сеть точек, тем отчетливее выступает ее контур. Соединяя построенные точки линией, характер которой учитывает положение промежуточных точек1*, мы и получаем линию, определяемую данным уравнением (1) (рис. 20). Эта линия называется параболой.
Некоторые элементарные задачи с решением
Если известно уравнение линии, то легко могут быть решены простейшие задачи, связанные с расположением этой линии на плоскости.
Задача 1. Заданы уравнение линии К и координаты точки М (а, Ь). Определить, лежит точка М на линии К или нет.
Иными словами, требуется узнать, проходит линия К через точку М или не проходит.
На основании понятия уравнения линии получаем правило:
чтобы определить, лежит ли точка М на данной линии К, нужно в уравнение этой линии подставить координаты нашей точки. Если при этом уравнение удовлетворится (т. е. в результате подстановки получится тождество), то точка лежит на линии; в противном случае, если координаты точки не удовлетворяют уравнению линии, данная точка не лежит на линии.
Для того чтобы иметь возможность судить о положении промежуточных точек линии, мы должны предварительно изучить общие свойства уравнения этой линии (подробнее см. в гл. XI).
В частном случае линия проходит через начало координат тогда и только тогда, когда уравнение линии удовлетворяется при х = 0 и у — 0.
Пример:
Определить, лежат ли на ней точки М (-3, 4) и N (4, -2).
Решение:
Подставляя координаты точки М в уравнение (1), получаем тождество
Следовательно, точка М лежит на данной окружности.
Аналогично, подставляя координаты точки N в уравнение (1), будем иметь
Следовательно, точка N не лежит на данной окружности.
Задача 2. Найти точку пересечения двух линий, заданных своими уравнениями.
Точка пересечения одновременно находится как на первой линии, так и на второй. Следовательно, координаты этой точки удовлетворяют уравнениям обеих линий. Отсюда получаем правило:
чтобы найти координаты точки пересечения двух линий, достаточно совместно решить систему их уравнений.
Если эта система не имеет действительных решений, то линии не пересекаются.
Пример:
Найти точки пересечения параболы у = х2 и прямой у — 4.
Решение:
получаем две точки пересечения: А (-2, 4) и В (2, 4).
Задача 3. Найти точки пересечения данной линии с осями координат.
Эта задача является частным случаем задачи 2. Учитывая, что уравнение оси Ох есть у = 0, получаем правило: ‘
чтобы найти абсциссы точек пересечения данной линии с осью Ох, в уравнении этой линии нужно положить у = 0 и решить полученное уравнение относительно х.
Аналогично, так как уравнение оси Оу есть х — 0, то получаем правило:
чтобы найти ординаты точек пересечения данной линии с осью Оу, нужно в уравнении этой линии положить д: = 0 и решить полученное уравнение относительно у.
Пример:
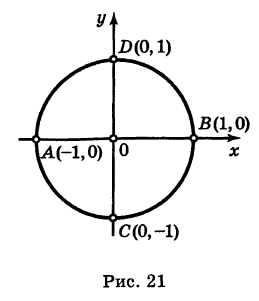
Найти точки пересечения окружности 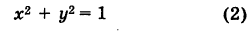
Решение:
Полагая у = 0 в уравнении (2), получаем х2= 1, т. е. х1 = -1 и х2 = 1. Отсюда находим две точки пересечения данной окружности с осью Ох (рис. 21): А (-1, 0) и В (1, 0).
Аналогично, полагая х = 0 в уравнении (2), получаем у2 = 1, т. е. ух = -1 и у2 = 1. Следовательно, имеются две точки пересечения данной окружности с осью Оу (рис. 21): С (0, -1) и D (0, 1).
Две основные задачи аналитической геометрии на плоскости
Резюмируя содержание этой главы, можно сказать, что всякой линии на плоскости соответствует некоторое уравнение между текущими координатами (х, у) точки этой линии. Наоборот, всякому уравнению между х и г/, где х и у — координаты точки на плоскости, соответствует, вообще говоря, некоторая линия, свойства которой вполне определяются данным уравнением.
Отсюда, естественно, возникают две основные задачи аналитической геометрии на плоскости.
Задача 1 .Дана линия, рассматриваемая как множество точек. Составить уравнение этой линии.
Задача 2. Дано уравнение некоторой линии. Изучить по этому уравнению ее геометрические свойства (форму и расположение).
Алгебраические линии
Определение: Линия называется линией (или кривой) n-го порядка(п = 1, 2. ), если она определяется уравнением п-й степени относительно текущих прямоугольных координат.
Такие линии называются алгебраическими. Например, линии
являются кривыми соответственно первого, второго и третьего порядков.
Общий вид кривых первого порядка есть
где коэффициенты А и Б не равны нулю одновременно, т. е. 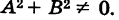
Общий вид кривых второго порядка следующий:
где коэффициенты А, Б и С не равны нулю одновременно, т. е.
Заметим, что не всякому уравнению второго порядка соответствует действительная кривая. Например, уравнению 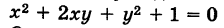
В следующих главах мы подробно изучим кривую первого порядка (прямую линию) и рассмотрим важнейшие представители кривых второго порядка (окружность, эллипс, гипербола, парабола).
Уравнение кривой n-го порядка может быть записано в следующем виде:
где хотя бы один из старших коэффициентов apqt т. е. таких, что p + q = п, отличен от нуля ( 
Отметим важное свойство: порядок кривой (1) не зависит от выбора прямоугольной системы координат.
Действительно, выбирая другую систему прямоугольных координат О’х’уна основании формул перехода имеем
где 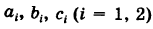
Отсюда уравнение кривой (1) в новых координатах О’х’у’ будет иметь вид
где п’ — порядок преобразованной кривой. Очевидно, что п’
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Аналитическая геометрия на плоскости и в пространстве. 1 страница
В этой главе мы изучим фигурах первого и второго порядка на плоскости и в пространстве.
§2.1.Декартова прямоугольная система координат.
2.1.1. Определение. Аффинной (декартовой) системой координатв трехмерном пространстве называется совокупность некоторой точки и произвольного базиса. При этом точка называется началом координат, а прямые, проходящие через начало координат в направлении базисных векторов – осями координат: первая – осью абсцисс (ОХ), вторая – осью ординат (ОY), третья – осью аппликат (OZ).
Аналогично определяются аффинные системы координат на плоскости и прямой.
2.1.2. Определение. Вектор, соединяющий начало координат с некоторой точкой, называется радиусом-вектором этой точки.
2.1.3. Определение. Координатами точки в аффинной системе координат называются координаты ее радиуса-вектора.
2.1.4. Определение. Аффинная система координат, базис которой является ортонормированным, называется прямоугольной декартовой системой координат.

Пусть новая система координат 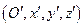
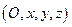
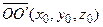


2.1.6. Кривые и поверхности.
Одним из основных вопросов аналитической геометрии является исследование линий на плоскости и поверхностей в пространстве.
2.1.6.1. Определение. Уравнение f(x, y) = 0 называется уравнением линии l на плоскости, если этому уравнению удовлетворяют координаты х, у всех точек М(х, у), лежащих на линии, и не удовлетворяют координаты ни одной точки P(х, у), не лежащей на кривой:
f(x, y) = 0 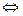
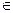
f(x, y) 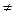
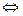

2.1.6.2. Определение. Уравнение F(x, y, z) = 0 называется уравнением поверхности 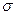
F(x, y, z) = 0 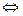
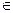
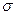
F(x, y, z) 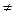
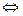

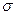
2.1.7. Две основные задачи аналитической геометрии.
I.Дано некоторое множество точек плоскости (пространства), обладающее некоторым набором свойств. Требуется составить уравнение (или систему уравнений), которое в некоторой системе координат задает это множество точек.
II (обратная). В заданной системе координат некоторое множество точек плоскости (пространства) описывается заданным уравнением (или системой уравнений). Требуется определить вид и основные свойства этого множества и построить его эскиз.
§2.2.Простейшие задачи аналитической геометрии.
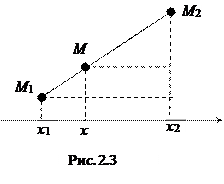
2.2.1. Нахождение длины отрезка.
Пусть в заданной декартовой прямоугольной системе координат имеется две точки 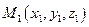

Вектор 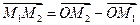
Следовательно, длина отрезка 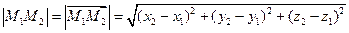
2.2.2. Деление отрезка в заданном отношении.
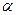
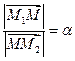
Запишем векторное равенство 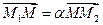
В частном случае 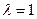
§2.3. Прямая на плоскости.
2.3.1. Общее уравнение прямой.
2.3.1.1. Определение. Ненулевой вектор 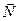
2.3.1.2. Теорема. (Общее уравнение прямой)

Пусть на плоскости задана точка 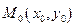
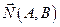
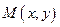
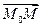
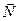

(скалярное произведение ортогональных векторов равно нулю).
Запишем последнее равенство в координатной форме: 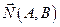
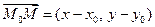
Ах + Ву + (–Ах0 – Ву0) = 0. Обозначим С = –Ах0 – Ву0, тогда 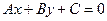
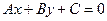
2.1.3.3. Определение. Уравнение вида
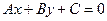
называется общим уравнением прямой.
2.1.3.4. Определение. Уравнение вида
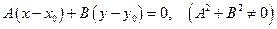
называется уравнением прямой, проходящей через точку 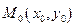
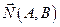
2.1.3.5. Определение. Линии, которые в декартовой прямоугольной системе координат задаются уравнениями первой степени, называются линиями первого порядка.
2.3.1.6. Теорема. (О линиях первого порядка на плоскости)
Линиями первого порядка на плоскости являются прямые, и только они.
То, что прямая на плоскости задается уравнением вида 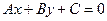
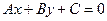

Пусть 

Вычтем полученное равенство из уравнения (2.1), получим
то есть уравнение прямой, проходящей через точку 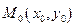
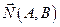

Таким образом, доказано, что всякое уравнение вида (2.1) при условии 
2.3.1.7. Теорема. (О перпендикулярности прямой и вектора на плоскости)
Для того, чтобы прямая, заданная общим уравнением, была перпендикулярна вектору на плоскости, необходимо и достаточно, чтобы координаты вектора были пропорциональны коэффициентам при переменных общего уравнения прямой, т.е.
Очевидно, перпендикулярность прямой и вектора эквивалентно коллинеарности вектора и нормального вектора прямой, следовательно, по критерию коллинеарности (Следствие из теоремы 1.5.6) получаем требуемое.
2.3.1.8. Частные случаи общего уравнения прямой на плоскости.
1. 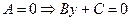
2. 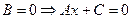
3. 
4. 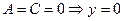
5. 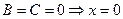
2.3.2. Уравнение прямой с угловым коэффициентом.
2.3.2.1. Определение. Углом наклона прямой называется любой направленный угол, на который надо повернуть ось Ох, чтобы получить одно из направлений прямой.
Очевидно, все углы наклона прямой отличаются друг от друга на величину 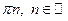
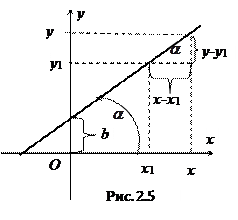
2.3.2.2. Вывод уравнения прямой с угловым коэффициентом.
Рассмотрим точку 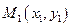
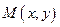
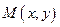
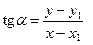
Обозначим 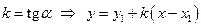
Полагая 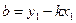
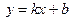
Геометрический смысл коэффициента 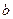
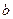
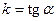
Уравнение вида (2.3) называется уравнением прямой с угловым коэффициентом.
Так как 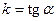
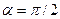
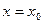
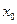
2.3.3. Связь между общим уравнением прямой и уравнением прямой с угловым коэффициентом.
Запишем уравнение прямой с угловым коэффициентом 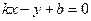
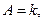
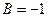
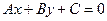
Обратный переход: если в уравнении 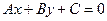
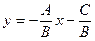
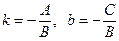
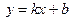
2.3.4. Уравнение прямой в отрезках.
Рассмотрим прямую, не проходящую через начало координат и заданную своим общим уравнением 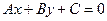
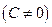


Обозначая 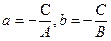
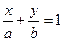
которое называется уравнением прямой в отрезках.
Положив в этом уравнении х = 0, получим y = b; положив у = 0, получаем х = а. Таким образом, параметры а и b равны, соответственно, абсциссе и ординате концов отрезков, отсекаемых прямой на осях Ох и Оу. Отметим, что в отрезках может быть записана любая прямая, не проходящая через начало координат.
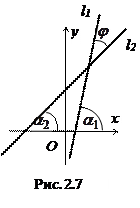
прямая l2 задана уравнением у = k2х + b2; тогда 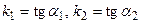
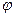
Так как 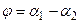
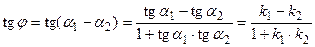
Таким образом, 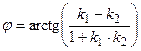
Если прямые заданы своими общими уравнениями
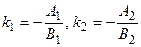
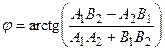
2.3.5.1. Условия параллельности и перпендикулярности прямых на плоскости.
Из выражений для тангенса угла между прямыми следуют условия параллельности и перпендикулярности прямых:
В случае параллельности прямых l1|| l2 тангенс угла между ними
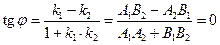
следовательно, k1 = k2, или А1В2 = А2В1, или 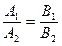
В случае параллельности прямых 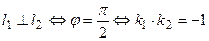
2.3.6. Расстояние от точки до прямой на плоскости.

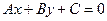
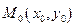
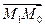
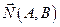


Из принадлежности точки М1 прямой l следует, что 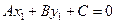

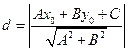
Таким образом, чтобы найти расстояние от точки до прямой, достаточно подставить координаты точки в общее уравнение прямой и полученное число разделить на длину нормального вектора.
§2.4. Плоскость в пространстве.
2.4.1. Общее уравнение плоскости.
2.4.1.1. Определение. Вектор, перпендикулярный к плоскости, называется ее нормальным вектором.
2.4.1.2. Теорема. (Общее уравнение плоскости).

Пусть в пространстве задан ненулевой вектор 
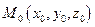
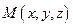
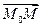
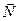
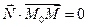
(скалярное произведение ортогональных векторов равно нулю).
В координатном виде это уравнение имеет вид
Преобразуем это уравнение: 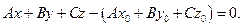
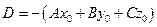
2.4.1.3. Определение. Уравнение вида
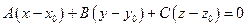
называется уравнением плоскости, проходящей через точку 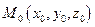

2.4.1.4. Определение. Уравнение вида
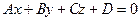
называется общим уравнением плоскости.
2.4.1.5. Связка плоскостей.
Связкой плоскостей называют совокупность плоскостей, проходящих через одну точку. Очевидно, уравнение 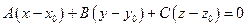
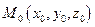
2.4.1.6. Определение. Поверхность в пространстве, которая в декартовой прямоугольной системе координат задается уравнением первой степени, называется поверхностью первого порядка.
2.4.1.7. Теорема. (О поверхностях первого порядка в пространстве).
Поверхностями первого порядка в пространстве являются плоскости, и только они.
Поскольку мы уже доказали в теореме 2.4.1.2, что плоскость можно задать уравнением первого порядка, осталось доказать, что уравнение 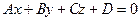
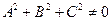
Пусть 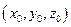
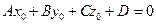
Вычтем полученное равенство из уравнения (2.7), получим
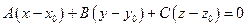
то есть уравнение плоскости, проходящей через точку 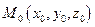

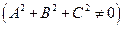
Таким образом, доказано, что всякое уравнение вида (2.7) при условии 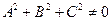
2.4.1.8. Частные случаи общего уравнения плоскости.
1. 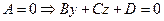
2. 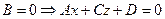
3. 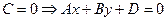
4. 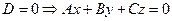
5. 
6. 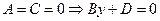
7. 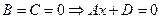
8. 
9. 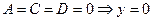
10. 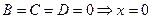
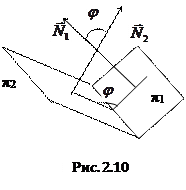
Пусть даны две плоскости
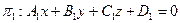
и 
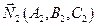
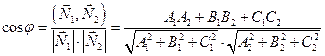
Если требуется определить острый угол между плоскостями, то
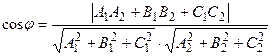
Из формулы угла между плоскостями следуют условия параллельности и перпендикулярности плоскостей.
Дата добавления: 2016-04-14 ; просмотров: 2688 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Понятие об уравнении линии на плоскости и в пространстве. Уравнение окружности.
Уравнением линии на плоскости в декартовой системе координат называют уравнение: F(х;у)=0, которому удовлетворяют координаты (х;у) любой точки этой линии и не удовлетворяют координаты ни одной точки, которые не принадлежат ей.
Линия в пространстве задаётся в общем случае как линия пересечения некоторых поверхностей S1 и S2 .
называется уравнением линии в пространстве.
Окружностью называется линия, каждая точка М(х;у) на которой находится на одинаковом расстоянии 


В прямоугольной системе координат уравнение окружности имеет вид
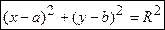
где (a; b) — координаты её центра, 
В частности, если центр окружности совпадает с началом координат, т.е. a=0 , b=0 , то уравнение окружности примет вид:
Уравнение прямой. Различные виды уравнений прямой.
Общее уравнение прямой:
1.
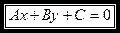
где 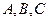



Частные случаи этого уравнения:













Нахождение углов между прямыми на плоскости. Условия параллельности и перпендикулярности прямых.
Если в пространстве заданы направляющий вектор прямой L
и уравнение плоскости
Ax + By + Cz + D = 0,
то угол между этой прямой и плоскостью можно найти используя формулу
| sinφ = | | A · l + B · m + C · n | |
| √A 2 + B 2 + C 2 · √l 2 + m 2 + n 2 |
Условия параллельности двух прямых:
а) Если прямые заданы уравнениями (4) с угловым коэффициентом, то необходимое и достаточное условие их параллельности состоит в равенстве их угловых коэффициентов:
б) Для случая, когда прямые заданы уравнениями в общем виде (6), необходимое и достаточное условие их параллельности состоит в том, что коэффициенты при соответствующих текущих координатах в их уравнениях пропорциональны, т. е.
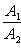

Условия перпендикулярности двух прямых:
а) В случае, когда прямые заданы уравнениями (4) с угловым коэффициентом, необходимое и достаточное условие их перпендикулярности заключается в том, что их угловые коэффициенты обратны по величине и противоположны по знаку, т. е.
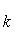

Это условие может быть записано также в виде
б) Если уравнения прямых заданы в общем виде (6), то условие их перпендикулярности (необходимое и достаточное) заключается в выполнении равенства
Уравнение прямой в пространстве: параметрические и канонические.
Если прямая проходит через две точки A(x1, y1, z1) и B(x2, y2, z2), такие что x1 ≠ x2, y1 ≠ y2 и z1 ≠ z2, то уравнение прямой можно найти используя следующую формулу
| x — x1 | = | y — y1 | = | z — z1 |
| x2 — x1 | y2 — y1 | z2 — z1 |
Параметрические уравнения прямой могут быть записаны следующим образом
 | x = l t + x0 |
| y = m t + y0 | |
| z = n t + z0 |
где (x0, y0, z0) — координаты точки лежащей на прямой,
Каноническое уравнение прямой в пространстве
Если известны координаты точки A(x0, y0, z0) лежащей на прямой и направляющего вектора n =
| x — x0 | = | y — y0 | = | z — z0 |
| l | m | n |
Уравнения плоскости.
Уравнение плоскости в прямоугольной системе координат Oxyz в трехмерном пространстве – это уравнение с тремя переменными x, y и z, которому удовлетворяют координаты любой точки заданной плоскости и не удовлетворяют координаты точек, лежащих вне данной плоскости.
Таким образом, уравнение плоскости обращается в тождество при подстановке в него координат любой точки плоскости. Если в уравнение плоскости подставить координаты точки, не лежащей в этой плоскости, то оно обратится в неверное равенство.
Всякое уравнение вида 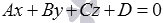
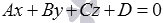
Уравнение 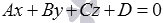
http://helpiks.org/7-85715.html
http://megalektsii.ru/s41911t7.html